Totaldruck

Der Totaldruck $p_{\mathrm {t} }$ (auch Gesamtdruck, Ruhedruck, Stagnationsdruck) beschreibt den Druck, der sich in einem strömenden Medium an einem Punkt einstellt, wo die Strömungsgeschwindigkeit isentrop (verlustfrei) bis nahezu zum Stillstand verringert wird; das ist häufig bei einer Staupunktströmung der Fall. Ein probates Mittel zur Messung des Totaldruckes ist das Pitotrohr.

Für inkompressible und für kompressible Fluide tragen unterschiedliche Komponenten zum Totaldruck bei.

Inkompressibler Fall (Flüssigkeit)

Bei einem inkompressiblen Fluid lässt sich nach der Bernoulli-Gleichung der Totaldruck aus zwei Größen berechnen, die die Strömung weit vor dem Staupunkt beschreiben. Der Totaldruck ist die Summe aus dem dort herrschenden statischen Druck $p$ , wie er von einem mit der Strömung mit bewegten Beobachter gemessen werden würde, und der spezifischen kinetischen Energie des strömenden Fluids (als dynamischer Staudruck $p_{\mathrm {dyn} }$ bezeichnet):[1]

{\begin{aligned}p_{\mathrm {t} }&=p+p_{\mathrm {dyn} }\\&=p+{\frac {\rho }{2}}\cdot v^{2}\end{aligned}}

mit

der Dichte $\rho$ des Fluids
der Strömungsgeschwindigkeit $v$ .

Durch den o. g. Zusammenhang lässt sich aus der Differenz von statischem Druck und Totaldruck, wie sie mit einer Prandtlsonde gemessen werden kann, die Strömungsgeschwindigkeit ermitteln.

Kompressibler Fall (Gas)

Bei einem kompressiblen Fluid besteht ein Zusammenhang zwischen Dichte, Druck und Temperatur, der in Verbindung mit einer Strömung auf die Gesetzmäßigkeiten der Gasdynamik führt.

Unterstellt man, dass innere Reibung (Reibung der Gasmoleküle untereinander) und äußere Reibung (Reibung des Gases mit der Rohrwandung) vernachlässigbar sind und die Höhe des Strömungspfades konstant ist, so bleibt der Totaldruck über den gesamten Strömungspfad konstant, während der statische Druck in Abhängigkeit von der Strömungsgeschwindigkeit variieren kann.

Einordnung und Abgrenzung

Der vereinfachte Energieansatz nach Bernoulli über die Druckänderung innerhalb einer Strömung gilt nur für Flüssigkeiten exakt.

Bei einer Gasströmung dagegen ändern sich mit dem statischen Druck auch Dichte und Temperatur des Mediums. Dies schlägt sich in der inneren und der kinetischen Energie des Mediums bzw. der Strömung nieder und muss deshalb im Energieansatz berücksichtigt werden.

Die erweiterte Leistungsgleichung (Energie pro Zeit) nach Bernoulli entlang des Strömungspfades eines reibungsfrei strömenden idealen Gases lautet damit:

P=p_{\text{ruhe}}\cdot {\dot {V}}=p_{\text{s}}\cdot {\dot {V}}+{\dot {m}}\cdot c_{\text{v}}\cdot T+{\frac {1}{2}}\cdot {\dot {m}}\cdot {w^{2}}+{\dot {m}}\cdot g\cdot z={\text{konst}}\qquad (1)

Die einzelnen Summanden stehen dabei für folgende Anteile an der Leistung $P$ :

$p_{\text{s}}\cdot {\dot {V}}$	= Anteil der mechanischen Energie (Druck × Volumen = Kraft × Weg)
${\dot {m}}\cdot c_{\text{v}}\cdot T$	= Anteil der transportierten Wärmemenge bzw. der im Gas enthaltenen thermischen Energie
${\frac {1}{2}}\cdot {\dot {m}}\cdot {w^{2}}$	= Anteil der kinetischen Energie der bewegten Gasmasse
${\dot {m}}\cdot g\cdot z$	= Anteil der potentiellen Energie (Lageenergie) des Gases

Hierbei sind:

$p_{\text{s}}$	= statischer Druck (absolut)
${\dot {V}}$	= Volumenstrom (= Volumen pro Zeit)
${\dot {m}}$	= Massenstrom (= Masse pro Zeit)
$c_{\text{v}}$	= spezifische Wärmekapazität des Gases bei konstantem Volumen
$T$	= Temperatur des Gases (absolut)
$w$	= Strömungsgeschwindigkeit
$g$	= Schwerebeschleunigung
$z$	= geodätische Höhe

Unter der Annahme, dass der Anteil der potentiellen Energie vernachlässigbar ist (Strömung verläuft horizontal, d. h. $\Delta z=0$ ; die Dichte von Gasen ist in der Regel wesentlich geringer als bei Flüssigkeiten), kann der letzte Term der Gleichung (1) entfernt werden. Mit den Grundgleichungen

{\dot {V}}={\dot {m}}/\rho

\rho =p_{\text{s}}/(R_{\text{s}}\cdot T)

R_{\text{s}}=c_{\text{p}}-c_{\text{v}}

mit

$\rho$ = Dichte des Gases
$R_{\text{s}}$ = Spezifische Gaskonstante
$c_{\text{p}}$ = spezifische Wärmekapazität des Gases bei konstantem Druck

folgt aus der restlichen Gleichung:

${\begin{aligned}\Rightarrow {\frac {P}{\dot {V}}}=p_{\text{ruhe}}&=\underbrace {p_{\text{s}}+\rho \cdot c_{\text{v}}\cdot T} _{\rho \cdot c_{\text{p}}\cdot T}+{\frac {1}{2}}\cdot \rho \cdot w^{2}={\text{konst}}\qquad {\text{(2)}}\end{aligned}}$

Einfluss der Geschwindigkeit

Geschwindigkeitsabhängigkeit der Temperatur

Geschwindigkeitsabhängigkeit des Druckes

jeweils bei einer Luftströmung mit

T_{\text{t}}=20{\text{°C}}

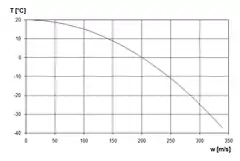
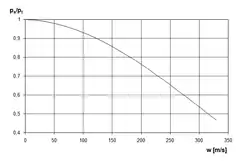
Gleichung (2) besagt, dass sich bei stationärer, wärmeisolierter Strömung eines idealen Gases die Temperatur des Gases mit zunehmender Strömungsgeschwindigkeit verringert und umgekehrt, sofern kein Energieaustausch mit der Umgebung stattfindet. Bei Zunahme der Strömungsgeschwindigkeit wird quasi ein Teil der ungerichteten mikroskopischen Molekülgeschwindigkeit (Temperatur) in eine gerichtete makroskopische Geschwindigkeit umgeformt.

Ähnlich verhält es sich mit dem Druck. Auch hier verringert sich der statische Druck mit zunehmender Strömungsgeschwindigkeit, da die Molekülgeschwindigkeit (und damit der Impulsaustausch) senkrecht zur Wandung zugunsten der Strömungsgeschwindigkeit verringert wird.

Bei einer Strömungsgeschwindigkeit von 0 m/s sind statischer Druck und Totaldruck identisch, ebenso statische Temperatur und Ruhetemperatur.

Berechnung

Da der Totaldruck nur an einer Stelle gemessen werden kann, an dem die Strömungsgeschwindigkeit vernachlässigbar klein ist (daher auch die Bezeichnung Ruhedruck oder Stagnationsdruck), muss er in der Regel berechnet werden. Dies kann für ein ideales Gas wie folgt geschehen:

p_{\text{t,x}}=p_{\text{x}}\cdot \left[{\frac {1}{2}}+{\sqrt {{\frac {\kappa -1}{2\cdot \kappa }}\cdot R_{\text{i}}\cdot T_{\text{t,x}}\cdot \left({\frac {\dot {m}}{A_{\text{x}}\cdot p_{\text{x}}}}\right)^{2}+{\frac {1}{4}}}}\ \right]^{\frac {\kappa }{\kappa -1}}\qquad (3)

Hierbei sind:

$p_{\text{t,x}}$	= Totaldruck an der Stelle $x$
$p_{\text{x}}$	= statischer Druck an der Stelle $x$
$\kappa$	= Isentropenexponent (z. B. bei Luft: $\kappa =1{,}4$ )
$R_{\text{i}}$	= individuelle Gaskonstante
$T_{\text{t,x}}$	= Ruhetemperatur an der Stelle $x$
${\dot {m}}$	= Massenstrom
$A_{\text{x}}$	= Querschnittsfläche des Strömungspfades an der Stelle $x$ .

Da bei einem idealen Gas die Ruhetemperatur entlang eines wärmeisolierten Strömungspfades, bei welchem die Strömungsgeschwindigkeit vernachlässigbar ist, konstant bleibt (so auch bei der Druckabsenkung durch Reibung/Drosselung), kann sie in der Regel an einer beliebigen Stelle entlang des Strömungspfades erfasst werden. Ob die Strömung als wärmeisoliert betrachtet werden kann, hängt neben der Wärmeleitfähigkeit der Umgebung auch davon ab, wie groß die Temperaturunterschiede zwischen der Gasströmung und der Umgebung sind, und wie groß das Verhältnis von Oberfläche zu Massenstrom ist.

Gleichung (3) unterstellt weiterhin, dass das Strömungsprofil der Gasströmung eine rechteckige Geschwindigkeitsverteilung aufweist. Dies ist bei turbulenter Strömung (welche sich bei höheren Geschwindigkeiten einstellt und bei der es überhaupt erst zu nennenswerten Unterschieden zwischen dem Totaldruck und dem statischen Druck kommt) auch nahezu gegeben. Wird jedoch nach dem statischen Druck für ein beliebiges, d. h. zumindest teilweise laminares, Strömungsprofil gesucht, so müssen numerische Verfahren angewendet werden, da sich Gleichung (3) offensichtlich nicht nach dem statischen Druck umstellen lässt.

Ausströmvorgang aus einem Behälter und Diffusor

Beim Ausströmvorgang aus einem Behälter über eine gut gerundete Düse (nahezu reibungsfreie Ausströmung mit in der Regel vernachlässigbarem Wärmeübergang) entspricht der Totaldruck, der zum statischen Druck im Halsteil der Düse korrespondiert, dem Behälterinnendruck.

Über einen Diffusor mit geringem Erweiterungswinkel kann der statische Druck am Diffusoreintritt ebenfalls weitestgehend auf den Totaldruck zurückgeführt werden, solange die Strömungsgeschwindigkeit am Eintritt des Diffusors unter der zugehörigen Schallgeschwindigkeit liegt.

Anwendung

In der technischen Praxis ist es häufig sinnvoller, mit dem „korrekten“ Totaldruck zu arbeiten anstatt mit dem in der Regel einfach und direkt messbaren statischen Druck. Leider wird dies häufig nicht beachtet und führt zu weiteren Fragen und Problemen. Zwei Beispiele aus dem Bereich der Durchflussmessung und Durchflusskennwertebestimmung an pneumatischen Bauteilen sollen diesen Sachverhalt verdeutlichen.

Beispiel 1

Wird an einem strömungsgünstigen Diffusor der Vordruck aufgrund der unterschiedlichen Anschlussquerschnitte mit einem kleineren Druckmessrohr (Rohr, an welchem sich der statische Druck der Strömung rechtwinklig zur Strömungsrichtung abgreifen lässt) und der Hinterdruck mit einem größeren Druckmessrohr gemessen, so tritt das Paradoxon auf, dass der Hinterdruck größer ist als der Vordruck (solange die Schallgeschwindigkeit im Diffusor nicht überschritten wird). Das Medium strömt also scheinbar vom niedrigeren Druck zum höheren statischen Druck.

Betrachtet man die Strömung jedoch unter dem Aspekt der Ruhedrücke, so wird der Ruhedruck in Strömungsrichtung niemals zunehmen, sondern bestenfalls nahezu konstant bleiben.

Beispiel 2

Ein gängiger Durchflusskennwert an pneumatischen Komponenten ist der qnN nach VDI 3290. Beim qnN wird der korrelierende Durchfluss zu einem statischen Vor- bzw. Eingangsdruck von 6 bar und einem statischen Ausgangs- bzw. Hinterdruck von 5 bar gemessen. Wird der qnN an einer Ventilinsel (Einheit mit gemeinsamem Versorgungsanschluss und mehreren individuell schaltbaren Einzelventilen) bestimmt, so tritt der Effekt auf, dass der Quotient aus Durchfluss dividiert durch Anzahl geschalteter (identischer) Ventile nicht konstant bleibt (oder sogar abnimmt, wie man vielleicht aufgrund einer internen Begrenzung vermuten könnte), sondern mit jedem weiteren durchgeschalteten Ventil progressiv zunimmt. Ursache dieses Effektes ist, dass der statische Eingangsdruck durch aktives Nachregeln konstant gehalten wird, der unsichtbare Ruhedruck damit aber stetig zunimmt und an den letzten Ventilscheiben zu einem erhöhten Staudruck führt, was in einem vergrößerten Durchfluss resultiert.

Literatur

Verband Deutscher Maschinen- und Anlagenbau: VDMA Einheitsblatt 24 575: Durchflussmessung von Pneumatikbauteilen. Anwendung der ISO 6358:1989 unter Berücksichtigung des Einflusses der Strömungsgeschwindigkeit.
Werner Wunderlich, Erwin Bürk, Wolfgang Gauchel: Messen in der Fluidtechnik/Durchflussmessung. Besonderheiten in der Pneumatik. In: O + P. Fluidtechnik für Maschinen- und Anlagenbau, 2010, April, ISSN 0341-2660

Einzelnachweise

TU Graz: Rohrströmung, Profilströmung. (PDF; 792 kB) Archiviert vom Original am 29. Januar 2016; abgerufen am 26. Juli 2013.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] TU Graz: Rohrströmung, Profilströmung. (PDF; 792 kB) Archiviert vom Original am 29. Januar 2016; abgerufen am 26. Juli 2013.