Schnittprinzip
Das Schnittprinzip (englisch free-body principle, principle of intersection[1]:75) ist ein unbegrenzt anwendbares[1]:91 und grundlegendes Prinzip der Mechanik. Interessierende Körper werden gedanklich aus ihrer Umgebung herausgelöst oder freigeschnitten, wesentliche Wechselwirkungen mit der Umgebung definiert und die Körper so einer Analyse zugänglich gemacht. Die Schnittführung ist dabei weitgehend beliebig und kann der jeweiligen Aufgabenstellung angepasst werden.[2] Der Körper kann ein Festkörper, eine Flüssigkeit, ein Gas oder ein System aus solchen sein.
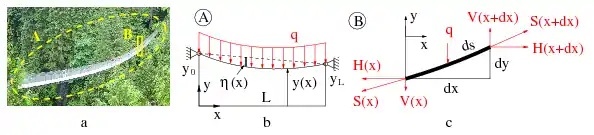
Die Abbildung zeigt ein Beispiel. Mittels des Schnitts A wird die Hängebrücke aus ihrer Umgebung heraus getrennt (a) und in ein mathematisches Modell überführt (b, wo die Streckenlast q die Gewichtskraft repräsentiert). Mit dem Schnitt B wird ein Teilstück bloßgelegt und die an ihm wirkenden Schnittgrößen H, S und V angetragen, um die Seillinie herzuleiten (c), siehe Seilstatik.
Geschichte
Das Schnittprinzip der Mechanik ist in seiner einfachsten Form die gedankliche Nachbildung des Bruchvorgangs beim Zugversuch, wie er schon bei Leonardo da Vinci und Galileo Galilei präformiert wurde.[3]
Die Erkenntnis über den Vorteil der Zerlegung wird Francis Bacon zugeschrieben, denn
„das Prinzip der Zerlegung […] blieb den Alten ganz verborgen, erst der große englische Naturphilosoph Bacon of Verulam sprach es um 1600 aus: ‚Man müsse die Natur zerschneiden.‘ Als Ganzes wären uns fast alle Naturerscheinungen unverständlich, sie wären so kompliziert und mannigfaltig, daß der Mensch bald jeden Versuch eines Verständnisses aufgeben müßte.“
Nach dem Begründer der theoretischen Physik
„lernen wir aus den Erscheinungen, dass die sich wechselseitig berührenden Theile der Körper von einander getrennt werden können.“
Diese Erkenntnis schlug sich in Newtons Prinzip Actio und Reactio nieder. Zur Formulierung des zweiten Newton’schen Gesetzes „Kraft gleich Masse mal Beschleunigung“ war gleichfalls das Schnittprinzip notwendig.[6]
Leonhard Euler entwickelte darauf aufbauend 1752 das Schnittprinzip, um ausgedehnte (auch deformierbare oder flüssige) Körper behandeln zu können: Wird ein beliebiger Teil eines Körpers in Gedanken herausgeschnitten, befolgt er für sich die newtonschen Gesetze der Mechanik, wobei die auf ihn wirkenden Kräfte die sind, die der restliche Körper an den Schnittflächen auf ihn ausübt (zuzüglich eventueller äußerer Kräfte wie Gewichtskraft etc.).[7]
Augustin-Louis Cauchy wandte dieses Schnittprinzip erfolgreich auch auf mechanische Spannungen an, die über die Schnittflächen verteilt sind. Entsprechend wird dieses Schnittprinzip auch als Spannungsprinzip von Euler-Cauchy bezeichnet.[8]
Allgemeines
Die mechanischen Wechselwirkungen finden immer zwischen materiellen Körpern oder den Teilchen, aus denen sie bestehen, statt. Drückt z. B. ein Teilchen T1 auf ein anderes T2 mit einer Kraft F, so tritt die Kraft F gleichzeitig auch an T1 als Wirkung von T2 auf, und zwar als eine Druckkraft in Richtung des Teilchens T1.
Beide Kräfte sind nach dem Prinzip „Actio und Reactio“ immer entgegengesetzt gleich groß.
An einem gegen andere Massen abgegrenzten System von Massen sind zwei Arten von Kräften zu unterscheiden: Zum Einen gibt es die inneren Kräfte, die zwischen jeweils zwei zum System gehörenden Massen wirken und daher immer paarweise entgegengesetzt auftreten. Zum Anderen gibt es die äußeren Kräfte, die zwischen jeder Systemmasse und einer sich außerhalb des Systems befindenden Masse wirken und die daher am System nur einmal auftreten. In der Summe heben sich die inneren Kräfte immer paarweise auf[9], so dass nur die äußeren Kräfte stehen bleiben.[10]
Anwendung in der Kontinuumsmechanik
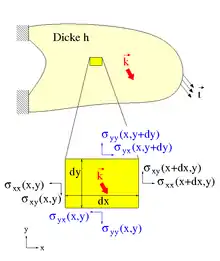
Aus Sicht der Kontinuumsmechanik kann das gesamte Universum als ein Kontinuum mit mehr oder weniger festen Bestandteilen angesehen werden. Die daraus hervorgehenden Theorien sind jedoch formal aufwendig und werden für die meisten, lokalen Untersuchungen nicht benötigt.[11] Stattdessen werden materielle Körper im Allgemeinen mit Hilfe des Schnittprinzips eingeführt.[2]:71 Aus dem Kontinuum wird durch Vorgabe einer Begrenzung der Körper herausgeschnitten, wodurch das Kontinuum in den Körper und seine Umgebung zerlegt wird. Die Begrenzung ist weitestgehend beliebig und kann der jeweiligen Aufgabenstellung angepasst werden.
Die inneren und äußeren Wechselwirkungen sind im Kontinuum immer flächig oder räumlich verteilt und werden, falls nötig, über entsprechende Gebiete zu Resultierenden integriert.
Es können auch – wie in der Abbildung rechts – (infinitesimal) kleine Teilkörper herausgelöst werden, um Bewegungsgleichungen der materiellen Punkte des Körpers herzuleiten, siehe beispielsweise Seilstatik und Cauchy-Eulersche Bewegungsgesetze. Insbesondere das Cauchy’sche Fundamentaltheorem zeigt die unbegrenzte Anwendbarkeit des Schnittprinzips in der Kontinuumsmechanik.[1]:91
Anwendung in der Technik
In der technischen Mechanik und Baustatik interessieren beim Freischneiden vor allem die Beanspruchungen an einer Stelle in einem Bauteil oder in einem System aus Bauteilen, die den an dieser Stelle anzubringenden Schnittreaktionen entsprechen.
Lageplan
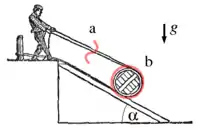
Ein Lageplan (siehe Abbildung) zeigt die räumliche Anordnung des betrachteten Körpers oder Systems. In ihm wird die Schnittführung eingezeichnet und gekennzeichnet.
Die gedanklichen Schnitte in dieser Abbildung trennen die betrachteten Körper von ihrer Umgebung (das Seil vom Mann und vom Fass und das Fass vom Seil und der Rampe). Die Trennlinie umfasst die gesamte weggeschnittene Umgebung (geschlossene Linie), die nicht immer vollständig eingezeichnet wird (durch die Luft führende Schnitte werden oft weggelassen).[Anmerkung 1]
Freikörperbild, Schnittreaktionen
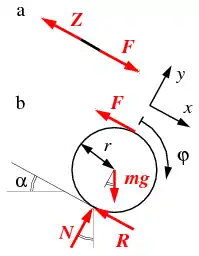
a) Schnittreaktion F und innere Seilkraft Z an der Schnittstelle[Anmerkung 2]
b) Die von der Gewichtskraft m·g erzeugte Hangabtriebskraft F (Vektorrichtung richtig hangabwärts! ) ist die Schnittreaktion[Anmerkung 3]
Der Lageplan wird zum sogenannten Freikörperbild abstrahiert. Vom freigeschnittenen Körper genügt die symbolische Darstellung der Schnittstelle (Schnittfläche). Von der weggeschnittenen Umgebung bleibt nur das für die Ermittlung der von ihr ausgehenden Schnittreaktionen unbedingt nötige Gegenständliche in Andeutung übrig (im Freikörperbild Fass, Rampenoberfläche und Rückhalteseil aus dem Lageplan).
Mit Hilfe des Freikörperbildes ist die Ermittlung der Schnittreaktionen relativ leicht möglich (im Freikörperbild die Zugkraft F am Seil; Z ist die innere Kraft im Seil).
Im Allgemeinen ist zu beachten:
- Fest verbundene Stäbe, Balken und andere feste Körper übertragen Kräfte und Momente.
- Seile, Ketten, Treibriemen und ähnliche biegeschlaffe Strukturen übertragen nur Zugkräfte in Seilrichtung. Durch Rollen werden solche Seilkräfte umgelenkt, bei Reibungsfreiheit ändert sich dabei ihr Betrag nicht.
- Ein Pendelstab, der an beiden Enden gelenkig gelagert ist, überträgt nur Zug- und Druckkräfte entlang seiner Achse.
- Gelenke übertragen – je nach Typ – einige Kräfte und Momente nicht. Andere Kräfte und Momente können aber – je nach Typ – übertragen werden.
- Kontaktkräfte an glatten, reibungsfreien Flächen wirken immer senkrecht zu den Flächen.
- Genauso üben Flüssigkeiten und Gase ihren statischen Druck immer senkrecht zu den benetzten Flächen aus.
- Reibkräfte wirken immer tangential zur Kontaktfläche entgegengesetzt zur Bewegungsrichtung des Körpers, an dem sie angreifen.
Zur Orientierung erhält die Zeichnung ein Koordinatensystem. In den verschiedenen Disziplinen (Baustatik, Maschinenbau, Punktmechanik) gibt es unterschiedliche Arten der Darstellung und Interpretation der Zeichen in den Skizzen.
Abbildung der Körper
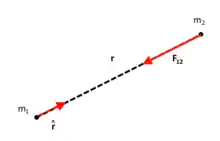
Das Freikörperbild ist eine Prinzipskizze, bei der es auf maßstabgerechte Darstellung nicht ankommt. Die einzelnen Körper werden skizziert, wobei Arme und Säulen durchaus zu Linien reduziert und ausgedehnte Körper – wie in der Abbildung rechts – auf Punkte zusammengezogen werden. Bei komplexen Bauteilen mit vielen Teilkörpern ähnelt ein Freikörperbild einer Explosionszeichnung, und es ist eine Sache der Geschicklichkeit, das Freikörperbild übersichtlich zu gestalten.
Abbildung der Kräfte und Momente
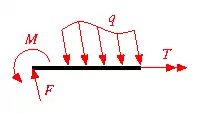
Kräfte werden als Pfeile, Streckenlasten als miteinander verbundene Pfeile und Momente als Doppelpfeile oder als um eine Drehachse gebogene einfache Pfeile dargestellt, siehe Abbildung rechts. Weil die relative Position der Kraftangriffspunkte und die Wirkungslinien der Kräfte für ein Kräftesystem von Belang sind, müssen die Angriffspunkte und ihre relativen Positionen aus dem Freikörperbild ersichtlich sein. Beim Eintrag der Kräfte muss bedacht werden, ob nur ermittelt werden soll, ob der Körper im Gleichgewicht ist, ob die Körper deformierbar sind oder als starr angenommen werden dürfen. Bei letzteren und allgemein bei Gleichgewichtsfragen dürfen Momente frei und Kräfte entlang ihrer Wirkungslinien verschoben werden. Bei der Ermittlung von Beanspruchungen und Deformationen dürfen die Kraftangriffspunkte nicht verlegt werden.
Nicht Darzustellendes
Das Freikörperbild ist nur eine von mehreren Zeichnungen, die für die Lösung mechanischer Systeme erstellt werden.
Die folgenden Merkmale von Systemen sollen in ihren Freikörperbildern ausdrücklich nicht vorkommen:
- nicht zum betrachteten System gehörende, insbesondere „weggeschnittene“ Körper (Die von ihnen ausgeübten Kräfte sind bereits eingetragen. Es besteht die Gefahr, Kräfte doppelt zu berücksichtigen.),
- Neben-, Rand- und andere Zwangsbedingungen sowie Lager (stattdessen sind die entsprechenden Zwangskräfte einzutragen),
- Kräfte und Momente, die der Körper auf seine Umgebung ausübt (Weil diese Kräfte und Momente nach dem Prinzip Actio und Reaction entgegengesetzt gleich groß sind zu denen, die auf den Körper ausgeübt werden, würden sich alle Kräfte und Momente auslöschen. Es gäbe keine eingeprägten Kräfte mehr.),
- innere Kräfte und Momente (Diese treten nur an Schnittflächen auf. Im Körper eingetragene innere Kräfte lassen befürchten, dass sie als eingeprägte Kräfte missverstanden werden.).
Diese auszuschließenden Details können bei Bedarf in anderen, ergänzenden Zeichnungen dargestellt werden.
Konkrete Abbildungen
Bisweilen werden Belastungen, Lagerreaktionen, Beanspruchungen und auch Schnittreaktionen vereinfachend in konkretere Abbildungen (etwa in technische Funktionsprinzipdarstellungen) eingetragen, wie die Bilder unten zeigen. Der Überblick geht dabei gegenüber Lageplänen und insbesondere Freikörperbildern leicht verloren.
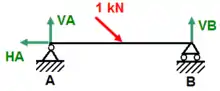 Die Lagerreaktionen sind als Vektoren bereits eingetragen. Die Lagersymbole sind verzichtbar. |
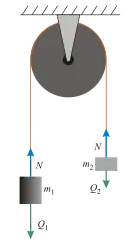 Das System ist nicht statisch, sondern dynamisch (die beiden Gewichtskräfte sind nicht gleich). Der Schritt bis zu einem Freikörperbild ist noch erheblich groß. |
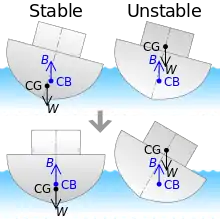 Die Auftriebskräfte B ersetzen den hydrostatischen Druck des Wassers, dessen Abbildung verzichtbar ist. |
In diesen Bildern tritt die Gefahr auf, dass manche Kräfte bei Anwendung des Schnittprinzips als eingeprägte Kräfte doppelt berücksichtigt werden, beispielsweise die Lagerreaktionen im linken Bild, die Seilkräfte im mittleren und die Auftriebskräfte im rechten Bild.
Siehe auch
Anmerkungen
- Bereits freigeschnittene Körper nochmals zu schneiden, birgt die Gefahr, dass leicht Fehler auftreten können, insbesondere dann, wenn im Freikörperbild schon vereinfachende Annahmen eingeflossen sind.
- Die kurze Linie zwischen den beiden Kraftvektoren deutet an, dass man mitunter von den beiden Ufern eines Schnittes spricht, von denen man dem einen (rechts im Freikörperbild) die Schnittreaktionen, dem anderen (links) die an der Schnittfläche des freigesschnittenen Teils vorhandenen inneren Kräfte und Momente bzw. Spannungen zuordnet.
- Die Kraftpfeile N und R stellen die Lagerreaktionen dar, die sich mit nicht eingezeichneten, sich ebenfalls aus der Gewichtskraft des Fasses ergebenden Kräften auf das Lager (Rampe und Gegenseil) kompensieren.
Literatur
- Bruno Assmann, Peter Selke: Technische Mechanik. 18. Auflage. Oldenbourg Wissenschaftsverlag, 2006, ISBN 3-486-58010-8, S. 99 (eingeschränkte Vorschau in der Google-Buchsuche).
- Alfred Böge: Technologie / Technik – für Fachgymnasien und Fachoberschulen. 5. Auflage. Friedr. Vieweg & Sohn, Braunschweig/Wiesbaden 1988, ISBN 978-3-528-44075-6, S. 5 f. (eingeschränkte Vorschau in der Google-Buchsuche).
- Dietmar Gross, Werner Hauger, Jörg Schröder, Wolfgang A. Wall: Technische Mechanik. Band 3: Kinetik. Springer DE, 2008, ISBN 978-3-540-68422-0, S. 191 f. (eingeschränkte Vorschau in der Google-Buchsuche).
Weblinks
- Beamex – Programm der TU Berlin, um Freizeichnungen anzulegen
Einzelnachweise
- P. Haupt: Continuum Mechanics and Theory of Materials. Springer, 2002, ISBN 978-3-642-07718-0 (englisch).
- H. Altenbach: Kontinuumsmechanik. Einführung in die materialunabhängigen und materialabhängigen Gleichungen. Springer, 2012, ISBN 3-642-24119-0, S. 71.
- Karl-Eugen Kurrer: The History of the Theory of Structures. Searching for Equilibrium. Ernst & Sohn, Berlin, ISBN 978-3-433-03229-9, S. 378 f.
- Georg Hamel: Elementare Mechanik. Ein Lehrbuch. Teubner, Leipzig / Berlin 1912, DNB 580933865, S. 5 (archive.org).
- Mathematische Principien der Naturlehre (Die Wolfers-Übersetzung). 1872, S. 388; Volltext (Wikisource)
- István Szabó: Geschichte der mechanischen Prinzipien. Springer, 2013, ISBN 978-3-0348-5301-9 (Eingeschränkte Vorschau S. 248 und S. 20 in der Google-Buchsuche [abgerufen am 3. Februar 2022]).
- Otto Bruns, Theodor Lehmann: Elemente der Mechanik I: Einführung, Statik. Vieweg, Braunschweig 1993, S. 92 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 3. Februar 2022]).
- Hans Georg Hahn: Elastizitätstheorie. Grundlagen der linearen Theorie und Anwendungen auf eindimensionale, ebene und räumliche Probleme (= Leitfäden der Angewandten Mathematik und Mechanik; 62). Teubner, Stuttgart 1985, DNB 850225965, S. 16 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 1. Dezember 2016]).
- Diese Aussage hat in der Mechanik den Stellenwert eines Axioms:
- In der Punktmechanik wirken innere Kräfte nach dem dritten Newton’schen Axiom immer paarweise entgegengesetzt und innere Drehmomente treten nicht auf, weil Massenpunkte nur Zentralkräfte aufnehmen können.
- In der Kontinuumsmechanik muss dem Boltzmann-Axiom zufolge jedes Volumenelement im statischen Gleichgewicht sein, sodass die resultierenden inneren Kräfte und Momente am Volumenelement null ergeben.
- H. Oertel (Hrsg.): Prandtl-Führer durch die Strömungslehre. Grundlagen und Phänomene. 13. Auflage. Springer Vieweg, 2012, ISBN 978-3-8348-1918-5, S. 15.
- H. Bertram: Axiomatische Einführung in die Kontinuumsmechanik. Wissenschaftsverlag, 1989, ISBN 3-411-14031-3, S. 67 f.