Wandschubspannung

Die Wandschubspannung (Formelzeichen $\tau _{w}$ , Dimension M L⁻¹ T ⁻², englisch wall shear stress) ist in der Strömungsmechanik die von einem Fluid (Flüssigkeit oder Gas) auf umströmte Wände ausgeübte, tangential wirkende Kraft pro Flächeninhalt und besitzt nach dieser Definition eine Richtung. Die Wandschubspannung ist der Impulsfluss durch das an die Wand angrenzende Volumen des Fluids und folgt aus der Reibung der Fluidelemente an der Wand und untereinander. In der Strömungsmechanik wird sowohl die gerichtete, vektorielle Form als auch ihr Betrag als Wandschubspannung bezeichnet.

Die Wandschubspannung ist eine zentrale Größe in der Grenzschichttheorie und der Aerodynamik und dient zur Ermittlung des Schubspannungswiderstands.

Definition

Die Wandschubspannung ${\vec {\tau }}_{w}$ ist definiert als der Quotient aus der Parallelkraft, die ein Fluid auf eine Wand ausübt, und der Fläche der Wand:

{\vec {\tau }}_{w}:={\frac {{\vec {F}}_{||}}{A}}\,,

mit

${\vec {\tau }}_{w}$ : Wandschubspannung
${\vec {F}}_{||}$ : Kraft parallel zur Wand
$A$ : Flächeninhalt der Wand, auf der die Kraft wirkt.

Im Gegensatz zum Druck ist die Wandschubspannung eine vektorielle (gerichtete) Größe.

Wenn der Basisvektor ${\hat {e}}_{x}$ in die Richtung der Wandschubspannung weist, dann wird die Komponente der vektoriellen Wandschubspannung in Wirkrichtung

\tau _{w}=|{\vec {\tau }}_{w}|={\vec {\tau }}_{w}\cdot {\hat {e}}_{x}

ebenfalls kurz als Wandschubspannung bezeichnet.

Einfluss der Fluideigenschaften

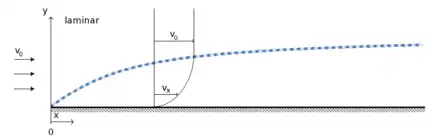
Ausbildung einer laminaren Grenzschicht zwischen der blauen Linie und einer flachen Oberfläche (untere Linie).

Wenn Fluidelemente an einer Wand entlangstreichen, dann werden sie durch Reibeffekte von der Wand mitgenommen, das heißt ihre Geschwindigkeiten sind bestrebt sich einander anzugleichen. Das Fluidelement überträgt Impuls auf die Wand, die dadurch eine Kraftwirkung erfährt. Umgekehrt übt auch die Wand eine Kraft auf das Fluid aus, dessen Geschwindigkeit sich dadurch verändert. Werden diese Kräfte auf ihre Wirkfläche bezogen, dann entstehen Spannungen. In einer Kontinuumsströmung tauschen die Fluidelemente und die Wand Impuls über die zwischen ihnen wirkenden Spannungen aus.

Die Newton’schen Fluide sind die in der Strömungsmechanik zumeist betrachteten Fluide und in ihnen ist die Wandschubspannung proportional zur Geschwindigkeitsdifferenz senkrecht zur Strömungsrichtung parallel zur Wand:

\tau _{w}=\eta \left.{\frac {\partial v_{x}}{\partial y}}\right|_{y=0}\,.

Wie im Bild strömt das Fluid in x-Richtung und die y-Richtung ist senkrecht zur Wand und hat ihren Ursprung an der Wand. Die Proportionalitätskonstante η ist die dynamische Viskosität (Dimension M L^–1 T ⁻¹, Einheit Pa s).

In nicht-Newton’schen Fluiden ist der Zusammenhang zwischen der Wandschubspannung und der Strömungsgeschwindigkeit nicht linear.

In idealen Flüssigkeiten und Gasen reiben die Fluidelemente nicht aneinander und ihre Wirkung auf die Wand ist ausschließlich senkrecht zur Wand. Entsprechend gibt es keine Schubspannungen im Fluid und die Wandschubspannung ist an allen Wänden immer null.

Kontinuumsmechanische Betrachtung

Die Schnittspannungen im Fluid und an seinen Grenzen ergeben sich in der Kontinuumsmechanik aus dem Cauchy’schen Spannungstensor ${\boldsymbol {\sigma }}$ (Dimension M L⁻¹ T ^–2, Einheit Pa). Die Schubspannungen sind die Nebendiagonalglieder des Spannungstensors. Der Spannungsvektor ${\vec {t}}_{y}$ an der Wand mit Normalenvektor ${\hat {e}}_{y}$ ist dann das Produkt ${\hat {e}}_{y}\cdot {\boldsymbol {\sigma }}={\vec {t}}_{y}\,.$ Wenn der Spannungsvektor von seiner Komponente in y-Richtung befreit wird, bleibt die vektorielle Wandschubspannung übrig

{\vec {\tau }}_{w}={\vec {t}}_{y}-({\hat {e}}_{y}\cdot {\vec {t}}_{y}){\hat {e}}_{y}

und das Skalarprodukt mit dem Basisvektor ${\hat {e}}_{x}$ in x-Richtung ergibt die skalare Wandschubspannung

\tau _{w}=|{\vec {\tau }}_{w}|={\vec {\tau }}_{w}\cdot {\hat {e}}_{x}={\vec {t}}_{y}\cdot {\hat {e}}_{x}={\hat {e}}_{y}\cdot {\boldsymbol {\sigma }}\cdot {\hat {e}}_{x}\,.

Der Cauchy’sche Spannungstensor erfüllt die Impulsbilanz und wirkt über die Materialeigenschaften des Fluids auf das Geschwindigkeitsfeld zurück.

Aus der Wandschubspannung abgeleitete Größen

Wandschubspannungsgeschwindigkeit

In von Grenzschichteffekten dominierten Strömungen in der Nähe von Wänden oder in Rohren ist die Wandschubspannungsgeschwindigkeit

u_{\tau }:={\sqrt {\frac {\tau _{w}}{\rho _{w}}}}

eine charakteristische Geschwindigkeit (Dimension L T ⁻¹, Einheit m/s). Im Nenner des Bruchs steht die Dichte des Fluids nahe der Wand.

Dimensionslose Koordinate

Mit der Wandschubspannungsgeschwindigkeit kann eine dimensionslose Koordinate

y^{+}:={\frac {u_{\tau }}{\nu }}\cdot y

gebildet werden, die bei der Modellierung von turbulenten Grenzschichten von Bedeutung ist.[1] Der Parameter $\nu ={\tfrac {\eta }{\rho }}$ ist die kinematische Viskosität (Dimension L² T ⁻¹, Einheit m²/s) des Fluids.

Reibungsbeiwert

Eine weitere wichtige Kennziffer in Grenzschichtströmungen ist der dimensionslose Reibungsbeiwert c_f. Er ist das Verhältnis der Wandschubspannung zum Staudruck der Außenströmung mit Strömungsgeschwindigkeit $u_{\infty }$ :

c_{f}:={\frac {|\tau _{w}|}{{\frac {\rho }{2}}u_{\infty }^{2}}}=2\left({\frac {u_{\tau }}{u_{\infty }}}\right)^{2}\,.

Ablösestellen

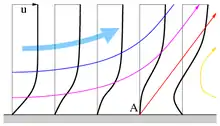
Umströmung einer Platte (grau) mit Grenzschicht (unter der blauen Linie), Stromlinien (rötlich), Ablösestelle A und wandparalleler Geschwindigkeit u

Nimmt der Druck nahe einer Wand in Strömungsrichtung zu, wird die äußere Strömung verzögert und die wandnahen langsameren Fluidelemente werden durch die Reibung noch stärker abgebremst. Ist die Verzögerung groß genug, tritt ein Rückstromgebiet auf, in dem sich Wirbel bilden (orange im Bild ganz rechts), und die Strömung löst sich von der Wand ab. An der Ablösestelle A verlässt eine Stromlinie (rot) die Wand in einem bestimmten Winkel und bildet eine Trennschicht zwischen der laminaren und der turbulenten Strömung. Bei Bildung einer turbulenten Grenzschicht wird diese durch die Wirbel aufgedickt (blaue Linie).

Die Ablösestelle ist dort, wo an der Wand der Gradient der wandparallelen Geschwindigkeit senkrecht zur Wand verschwindet, siehe die dicken, schwarzen, von unten nach oben verlaufenden Linien, die die horizontale Geschwindigkeitskomponente illustrieren. In Newton’schen Fluiden ist die Wandschubspannung an der Ablösestelle gleich null.[2]

Strömungen durch Rohre und Kanäle

Bei Strömungen in Rohrleitungen und Kanälen ist die Querschnittsfläche A und die vom Fluid benetzte Rohr- oder Kanalfläche W bekannt. Zwischen zwei Orten 1 und 2 müssen sich die Druckdifferenz und die auf der Wandfläche wirkende mittlere Wandschubspannung das Gleichgewicht halten:

(p_{1}-p_{2})A=W\tau _{w}\quad \rightarrow \quad \tau _{w}={\frac {A}{W}}(p_{1}-p_{2})=\lambda {\frac {\rho }{2}}v_{m}^{2}\,,

worin λ ein mit dem Reibungsbeiwert c_f verwandter Verlustbeiwert und $v_{m}$ die mittlere Fließgeschwindigkeit ist. Verschiedene Ansätze für die Druckdifferenz auf Grund von Geländeneigung oder für den Verlustbeiwert führen auf Näherungsformeln für die Strömungsgeschwindigkeiten (Fließformeln) oder die zu erwartenden Druckverluste.[3]

Siehe auch

Literatur

H. Oertel (Hrsg.): Prandtl-Führer durch die Strömungslehre. Grundlagen und Phänomene. 13. Auflage. Springer Vieweg, 2012, ISBN 978-3-8348-1918-5.

Weblinks

Erich Schülein: Optisches Verfahren zur Messung der Wandschubspannung. Abteilung Hochgeschwindigkeitskonfigurationen. Deutsches Zentrum für Luft- und Raumfahrt (DLR), abgerufen am 20. Januar 2016.

Einzelnachweise

Oertel (2012), S. 128f
Oertel (2012), S. 113
Oertel (2012), S. 149ff

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Oertel (2012), S. 128f

[2] Oertel (2012), S. 113

[3] Oertel (2012), S. 149ff