Erdbahn

Die Erdbahn ist die Umlaufbahn (oder Revolution) der Erde um die Sonne. Sie ist somit der Weg, den die Erde bei ihrem jährlichen Umlauf um die Sonne beschreibt.

Erdbahn
Mittlere elliptische Bahnelemente, bezogen auf die mittlere Ekliptik und das mittlere Äquinoktium zur Epoche J2000.0
Große Halbachse	1,000 001 017 8 AE 149 598 022,96 km	[1]
Numerische Exzentrizität	0,016 708 634 2	[1]
Neigung gegen die Ekliptik	0°	[1]
Ekliptikale Länge des Perihels	102,937 348 08°	[1]
Mittlere ekliptikale Länge der Erde zum Zeitpunkt J2000.0	100,466 456 83°	[1]
Mittlere siderische Bewegung	0,985 609 112 5°/Tag Periode: 365,256 363 2 Tage	[2]
Mittlere tropische Bewegung	0,985 647 358°/Tag Periode: 365,242 190 4 Tage	[2]

Bahngeometrie

Form

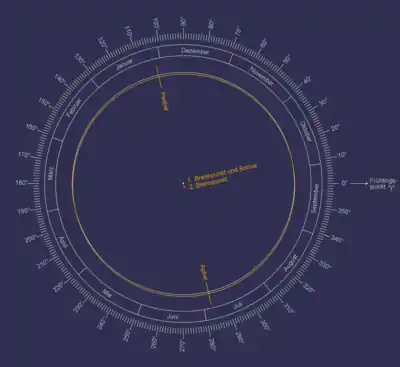
Maßstabsgetreue Darstellung der elliptischen Umlaufbahn der Erde (orange) im Vergleich mit einem Kreis (grau).

Die Erdbahn wird in guter Näherung durch eine Ellipse (Keplerbahn) mit der Sonne in einem der beiden Brennpunkte beschrieben, wie es vom ersten Keplerschen Gesetz verlangt wird.

Diese Ellipse weicht mit einer numerischen Exzentrizität $\varepsilon$ von 0,0167 nur sehr wenig von einer Kreisbahn ab. Für das bloße Auge ist der Unterschied zwischen einer solchen kreisähnlichen Ellipse und einem Kreis nicht feststellbar, sie erscheint wie ein etwas aus dem Mittelpunkt verschobener Kreis. Der sonnennächste Punkt ist das Perihel, der sonnenfernste Punkt ist das Aphel.

Die große Halbachse a der Erdbahn beträgt 149,598 Millionen Kilometer (eine Astronomische Einheit, AE). Dies ist gleichzeitig der mittlere Abstand zwischen Erde und Sonne, wenn die Mittelwertbildung gleichmäßig entlang der Bahn erfolgt.[3] Im Perihel ist die Erde 147,09 Millionen Kilometer[4] von der Sonne entfernt, während es im Aphel 152,10 Millionen Kilometer[4] sind. Diese beiden Extremwerte weichen vom Mittelwert nur um 1,67 % ab.[5]

Im zeitlichen Mittel beträgt der Abstand zwischen Erde und Sonne etwas mehr als eine AE (nämlich 1,00014 AE), da sich die Erde wegen ihrer ungleichförmigen Bahngeschwindigkeit etwas länger in Sonnenferne aufhält als in Sonnennähe.[3][6]

Ihre während eines Umlaufs unterschiedlichen Positionen auf der Umlaufbahn führen zur Parallaxe in den beobachteten Sternpositionen und zu Variationen von bis zu ±8,3 Minuten in den Lichtlaufzeiten zwischen Beobachtungsobjekt und Erde.

Die Länge der Erdbahn liegt bei etwa 940 Millionen km.[7] Die Erde bewegt sich pro Tag ca. 2,57 Millionen km auf ihrer Bahn, das sind etwa 202 Erddurchmesser. In einer Sekunde überstreicht die Strecke Erde–Sonne eine Fläche von über 2 Milliarden km²; dieser Wert ist nach dem zweiten Keplerschen Gesetz (dem „Flächensatz“) konstant.

Da die Erde einen massereichen Mond besitzt, kreist nicht wie bei mondlosen Planeten ihr Mittelpunkt auf der Kepler-Ellipse um die Sonne, sondern der gemeinsame Schwerpunkt von Mond und Erde (das Baryzentrum des Erde-Mond-Systems). Dieser Schwerpunkt liegt zwar noch im Erdinneren – in ca. 1700 km Tiefe – aber im Mittel etwa 4670 km vom Erdmittelpunkt entfernt. Der Erdmittelpunkt selbst kreist um den Schwerpunkt und vollführt folglich eine Schlangenlinie entlang der Ellipsenbahn, mit einer Schwingung pro Monat. Wenn von der „Erdbahn“ gesprochen wird, ist in der Regel die gleichmäßige Ellipsenbahn des Schwerpunkts gemeint, nicht die wellige Bahn der Erde selbst. Bei Angabe der Zeitpunkte, in denen bestimmte Bahnpunkte durchlaufen werden (z. B. der Frühlingspunkt oder das Perihel), ist zu unterscheiden, ob die Angabe sich auf den Erde-Mond-Schwerpunkt oder auf den Erdmittelpunkt bezieht. Siehe hierzu auch die Abschnitte →Lage der Apsiden und →Störungen in Länge.

Umlaufrichtung und Geschwindigkeit

Die Erde bewegt sich auf ihrer Bahn rechtläufig, also vom Polarstern aus betrachtet gegen den Uhrzeigersinn. Die durchschnittliche Bahngeschwindigkeit beträgt 29,7859 km/s[8] (107.229 km/h). Sie schwankt zwischen 30,29 km/s[4] im Perihel und 29,29 km/s[4] im Aphel.

Die Geschwindigkeit der Erde während ihres Umlaufs führt zur Aberration des beobachteten Sternenlichts. Ein weiterer Effekt der Bahngeschwindigkeit ist die im Jahresrhythmus schwankende Dopplerverschiebung der Wellenlänge des Lichts (bzw. enthaltener Spektrallinien) insbesondere von solchen Fixsternen, die sich nahe der Bahnebene befinden.[9]

Lage der Bahnebene

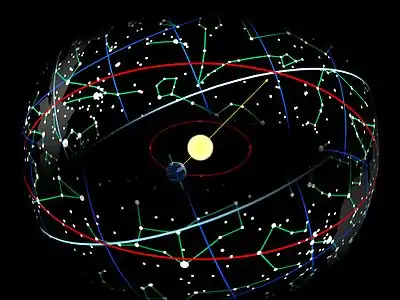
Die Ekliptik (großer roter Kreis) ist die an die Himmelskugel projizierte Erdbahn (kleiner roter Kreis). Der Himmelsäquator (türkis) ist der an die Himmelskugel projizierte Erdäquator.

Ekliptik und Himmelsäquator

Wie stets, wenn ein Himmelskörper seine Bahn unter dem Einfluss einer Zentralkraft durchläuft, liegt auch die Bahn des Erde-Mond-Schwerpunkts in einer Ebene. Es gibt keine seitwärts wirkenden Kräfte, welche die Bahn senkrecht zur Bahnebene krümmen könnten. Diese Bahnebene wird auch Ekliptikebene oder kurz Ekliptik genannt und dient unter anderem als Referenzebene für astronomische Koordinaten.

Denkt man sich die Bahnebene unendlich nach allen Seiten fortgesetzt, so ergibt ihre Schnittlinie mit der scheinbaren Himmelskugel einen Großkreis rund um den Himmel, den man ebenfalls als Ekliptik bezeichnet. Vom Mittelpunkt der Sonne aus betrachtet wandert die Erde entlang dieser Ekliptik-Linie einmal im Jahr rund um den Fixsternhimmel. Von der Erde aus gesehen ist es die Sonne, die im Verlaufe ihrer jährlichen Wanderung durch die Fixsterne entlang der Ekliptik läuft.[Anm. 1] Genaueres hierzu siehe im Abschnitt →Sonnenbahn sowie im Artikel →Sonnenstand. Die von der Sonne aus gesehene Position der Erde und die von der Erde aus gesehene Position der Sonne liegen einander an der Himmelskugel stets gegenüber. Die Charakteristika von Erd- und (scheinbarer) Sonnenbahn sind dieselben, und beide Betrachtungsweisen können benutzt werden, sie dürfen aber nicht miteinander verwechselt werden. Zum Frühlingsbeginn beispielsweise steht definitionsgemäß die von der Erde aus gesehene Sonne im Frühlingspunkt, während gleichzeitig die von der Sonne aus gesehene Erde im gegenüberliegenden Herbstpunkt steht.

Die Lage der Ekliptikebene im Raum lässt sich mit Hilfe der Pole der Ekliptik besonders einfach beschreiben. Es handelt sich um jene Punkte, in denen eine auf der Ekliptikebene senkrecht stehende Gerade die Himmelskugel durchstößt. Diese beiden einander auf der Himmelskugel gegenüberliegenden Punkte sind von allen Punkten des Ekliptik-Großkreises jeweils 90° entfernt. Lage und Verlauf der Ekliptik sind also vollständig festgelegt, wenn einer ihrer Pole gegeben ist. Zum Zeitpunkt J2000.0 – dem 1. Januar 2000 12:00 TT – befanden sich die Pole der Ekliptik auf den Koordinaten

Nördlicher Ekliptikpol:	RA:	18^h 0^m 0,0^s (exakt),	Dek:	+66° 33′ 38,588″[10]	(ein Punkt im Sternbild Drache)
Südlicher Ekliptikpol:	RA:	6^h 0^m 0,0^s (exakt),	Dek:	−66° 33′ 38,588″	(ein Punkt im Sternbild Schwertfisch)

Mit Hilfe der Pole lässt sich auch der Schnittwinkel von zwei einander schneidenden Ebenen leicht bestimmen – es ist einfach der Winkelabstand zwischen den zugehörigen Polen. Für den Nordpol der galaktischen Ebene beispielsweise gilt zum Zeitpunkt J2000.0:

Nördlicher galaktischer Pol:

RA: 12^h 51^m 26,2755^s,

Dek: +27° 7' 41,704"[11]

(ein Punkt im Sternbild Haar der Berenike)

Der Großkreisabstand zwischen dem nördlichen ekliptikalen und dem nördlichen galaktischen Pol beträgt 60,2°, um diesen Winkel ist also auch die Erdbahnebene gegen die galaktische Ebene geneigt.

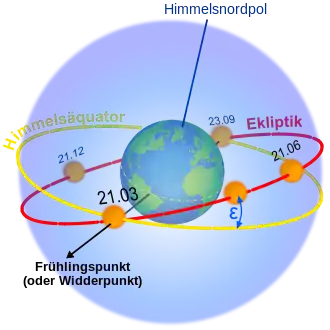
Die Rotationsachse der Erde steht nicht senkrecht auf der Bahnebene, sondern ist leicht geneigt. Entsprechend liegt auch die Äquatorebene der Erde bzw. ihre Projektion auf die scheinbare Himmelskugel, der Himmelsäquator, nicht in der Bahnebene. Der Winkel zwischen Ekliptikebene und Äquatorebene, die so genannte Schiefe der Ekliptik beträgt gegenwärtig etwa ε = 23,44°. Die Schnittlinie zwischen den beiden Ebenen zeichnet sowohl auf der Ekliptik als auch auf dem Äquator eine gemeinsame Referenzlinie aus. In einer der beiden durch die Referenzlinie definierten Richtungen steht die Sonne im Augenblick des Frühlingsbeginns, wenn die (aus Sicht der Erde) auf der Ekliptik wandernde Sonne den Himmelsäquator überschreitet und dabei durch den Schnittpunkt von Ekliptik und Äquator läuft. Die Richtung zu diesem „Frühlingspunkt“ wird als Nullpunkt für astronomische Koordinatensysteme verwendet. Gegenwärtig zeigt diese Richtung auf einen Punkt im Sternbild Fische.

Die Rektaszension wird vom Frühlingspunkt ausgehend rechtläufig entlang des Himmelsäquators gezählt, die Deklination senkrecht dazu. Die ekliptikale Länge wird vom Frühlingspunkt ausgehend rechtläufig entlang der Ekliptik gezählt, die ekliptikale Breite senkrecht dazu. Während eines gut 365 Tage dauernden Bahnumlaufs ändert sich die ekliptikale Länge der Erde um 360 Grad, sie legt also im Mittel ein knappes Grad pro Tag zurück.

Lage der Apsiden

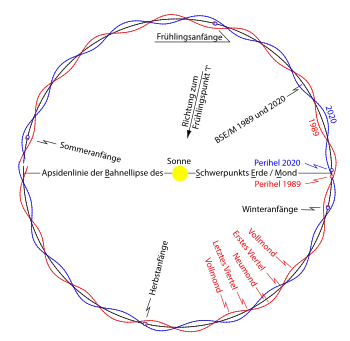
Bewegung der Erde auf Schlangenlinien um die Sonne (Details → Apsis (Astronomie))

Die Apsidenlinie – also die Verbindungslinie zwischen Perihel und Aphel – beschreibt die Ausrichtung der Erdbahnellipse innerhalb der Bahnebene. Das Perihel hatte zum Zeitpunkt J2000.0 die ekliptikale Länge 102.9° und zeigt daher gegenwärtig auf einen Punkt im Sternbild Zwillinge.[Anm. 2] Der Erde-Mond-Schwerpunkt durchläuft das Perihel gegenwärtig am 3. oder 4. Januar, das Aphel am 4. oder 5. Juli.

Der Erdmittelpunkt hingegen läuft entlang der mondbedingten Wellenlinie, welche wegen der von der gleichmäßigen Ellipse leicht abweichenden welligen Bahnform ihr eigenes Perihel hat. Dieses Erdmittelpunkts-Perihel liegt von Jahr zu Jahr – je nach der aktuellen Mondstellung – an einer etwas anderen Stelle der Bahn. Der Erdmittelpunkt passiert daher sein eigenes Perihel in deutlich unregelmäßigeren Abständen, in der Regel zwischen dem 2. und 5. Januar. Details hierzu werden im Artikel →Apsis (Astronomie) erläutert.

Bahnstörungen

Die Gravitationseinflüsse der anderen Planeten üben Störungen auf die Erdbahn aus, welche deren Form und Lage geringfügig aber kontinuierlich ändern.

Numerische Exzentrizität

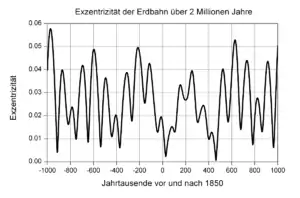
Langzeitverhalten der Exzentrizität der Erdbahn über zwei Millionen Jahre.

Die numerische Exzentrizität der Erdbahn beträgt gegenwärtig etwa 0,0167 und nimmt langsam ab. Für den Zeitraum zwischen etwa 4000 v. Chr. und 8000 n. Chr. wird der zeitliche Verlauf der Exzentrizität in guter Näherung beschrieben durch das Polynom[1]^:674f.[12]

{\begin{alignedat}{4}\varepsilon \,=&&\,0{,}016\,708\,6342&&\,-&\,0{,}000\,420\,3654&&\cdot t\\&\,-&\,0{,}000\,012\,6734&\cdot t^{2}&\,+&\,0{,}000\,000\,1444&&\cdot t^{3}\\&\,-&\,0{,}000\,000\,0002&\cdot t^{4}&\,+&\,0{,}000\,000\,0003&&\cdot t^{5}\\\end{alignedat}}

Dabei ist $t$ die in Julianischen Jahrtausenden ab der Standardepoche J2000 gemessene TDB. Für die Julianische Tageszahl $JD$ ist also

t={\frac {JD-2451545{,}0}{365250}}

.

Für Werte weit außerhalb des Bereichs $-6<t<6$ liefert das Polynom keine sinnvollen Werte.

Über größere Zeiträume betrachtet (siehe nebenstehendes Diagramm) kann die num. Exzentrizität Werte zwischen knapp 0,06 und beinahe Null annehmen. Das nächste Minimum erreicht sie mit 0,0023 etwa im Jahr 29500, ein noch tieferes Minimum mit 0,0006 etwa im Jahr 465000. Die Erdbahn wird dann vorübergehend praktisch kreisförmig sein.[12]

Von der Exzentrizität der Erdbahn hängt es ab, wie viel Sonnenstrahlung die Erde im Mittel während eines Jahres empfängt. Wenn die Erde im Abstand a (große Halbachse) von der Sonne die Bestrahlungsstärke S_a auf eine senkrecht zur Sonne gerichtete Fläche empfängt, so erhält sie im Abstand r auf ihrer Querschnittsfläche A die Einstrahl-Leistung

W\,=\,S_{a}\left({\frac {a}{r}}\right)^{2}\cdot A

Der während eines Jahres der Länge T empfangene Jahres-Energieeintrag ergibt sich durch Integration über die Zeit:[13]

W_{T}\,=\,\int _{0}^{T}Wdt\,=\,S_{a}A\int _{0}^{T}\left({\frac {a}{r}}\right)^{2}dt\,=\,{\frac {S_{a}AT}{\sqrt {1-\varepsilon ^{2}}}}

Der Jahres-Energieeintrag hängt also neben S_a auch von der numerischen Exzentrizität $\varepsilon$ ab: Er nimmt (bei gleich bleibendem S_a) zu, wenn die Exzentrizität zunimmt. Wegen ihrer geringeren Geschwindigkeit in Aphelnähe hält sich die Erde während ihres Bahndurchlaufs überdurchschnittlich lange in der sonnenfernen Hälfte der Umlaufbahn auf. Bei Zunahme der Exzentrizität entfernt sich dieser Teil der Umlaufbahn noch weiter von der Sonne. Dieser mit der Exzentrizität zunehmende Einstrahlungsverlust wird jedoch durch die quadratisch ansteigende Bestrahlungsstärke im zunehmend sonnennäheren Perihel mehr als ausgeglichen. Die durch die Veränderlichkeit der Exzentrizität verursachte langfristige Variation im Jahres-Energieeintrag beträgt nur Bruchteile eines Prozents, kann aber dennoch klimatologisch relevant sein.[13]

Die Hauptperiode der Schwankungen der Exzentrizität beträgt etwa 100.000 Jahre (siehe auch →Milanković-Zyklen).

Die über das Jahr gemittelte auf der Erde eintreffende Bestrahlungsstärke S₀ ist die Solarkonstante. Es ist[13]

S_{0}\,:=\,{\frac {W_{T}}{A\cdot T}}\,=\,{\frac {S_{a}}{\sqrt {1-\varepsilon ^{2}}}}

Die Solarkonstante ist also streng genommen nicht identisch mit der Bestrahlungsstärke S_a in der „mittleren Entfernung“ a. Die Abweichung beträgt jedoch nur etwa 0,1 Prozent.

Periheldrehung (Apsidendrehung)

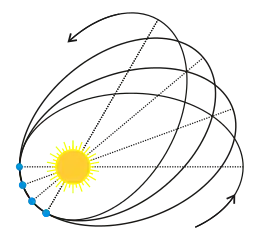
Schematische und stark übertriebene Darstellung der Periheldrehung (blaue Punkte: Perihel, gepunktete Linien: Ellipsenachse).

Die Achse der Ellipse (Apsidenlinie) dreht sich langsam in der Bahnebene, und zwar in derselben Richtung, in der die Erde die Bahn durchläuft (rechtläufig). Infolge dieser so genannten Periheldrehung wandert das Perihel in etwa 110.000 Jahren einmal bezüglich des Fixsternhintergrunds rund um die Sonne. Für den Zeitraum zwischen etwa 4000 v. Chr. und 8000 n. Chr. wird die mittlere ekliptikale Länge des Perihels in guter Näherung beschrieben durch das Polynom[1][Anm. 3][Anm. 4]

{\begin{alignedat}{4}\varpi \,=&&\,102{,}937\,348\,08^{\circ }&&\,+&\,3{,}225\,653\,583^{\circ }&&\cdot t\\&\,+&\,0{,}014\,798\,825^{\circ }&\cdot t^{2}&\,+&\,0{,}000\,039\,153^{\circ }&&\cdot t^{3}\\&\,-&\,0{,}000\,031\,778^{\circ }&\cdot t^{4}&\,+&\,0{,}000\,001\,328^{\circ }&&\cdot t^{5}\\\end{alignedat}}

wobei $t$ dieselbe Bedeutung hat wie in der Formel für die Exzentrizität. Der resultierende Winkel bezieht sich auf die mittlere Ekliptik und den (fixen) mittleren Frühlingspunkt zur Epoche J2000.0. Bezieht man die mittlere Länge des Perihels stattdessen auf den jeweils aktuellen mittleren Frühlingspunkt, der ihm rückläufig entgegen wandert (siehe Abschnitt →Jahreszeiten), so ändert sie sich entsprechend schneller:[1][Anm. 3]

{\begin{alignedat}{4}\varpi '\,=&&\,102{,}937\,348\,08^{\circ }&&\,+&\,17{,}194\,598\,028^{\circ }&&\cdot t\\&\,+&\,0{,}045\,688\,325^{\circ }&\cdot t^{2}&\,-&\,0{,}000\,017\,680^{\circ }&&\cdot t^{3}\\&\,-&\,0{,}000\,033\,583^{\circ }&\cdot t^{4}&\,+&\,0{,}000\,000\,828^{\circ }&&\cdot t^{5}\\&\,+&\,0{,}000\,000\,056^{\circ }&\cdot t^{6}&&&&\\\end{alignedat}}

Bezüglich dieses „Frühlingspunktes des Datums“ vollzieht das Perihel eine Bahnumrundung in etwa 21.000 Jahren. Da der Kalender an die Stellung der Sonne bezüglich des Frühlingspunktes gekoppelt ist, läuft der Zeitpunkt des Periheldurchgangs mit dieser Periode auch durch den Kalender: Um das Jahr 1600 fiel der Periheldurchgang zwischen den 26. und 28. Dezember; um das Jahr 2500 herum wird er auf den 10. bis 13. Januar fallen.[14][15]

Von der gegenseitigen Stellung von Perihel und Frühlingspunkt hängt es ab, wie die während des Jahres zur Verfügung stehende gesamte Sonneneinstrahlung sich auf die Jahreszeiten verteilt. Wenn eine Jahreszeit mit dem Periheldurchgang zusammenfällt (gegenwärtig der Nordhalbkugel-Winter), so erhält sie abstandsbedingt etwas mehr Einstrahlung von der Sonne als wenn sie 10500 Jahre später mit dem Apheldurchgang zusammenfällt. Sie ist gleichzeitig wegen der größeren Bahngeschwindigkeit der Erde auch die jeweils kürzeste Jahreszeit (vergleiche hierzu die Erläuterungen im Artikel →Jahreszeit).

Die auf den Frühlingspunkt des Datums bezogene Präzession des Perihels beeinflusst also die Ausprägung der einzelnen Jahreszeiten. Sie wird deshalb auch als „klimatische Präzession“[16] bezeichnet.

Ekliptik als Referenz

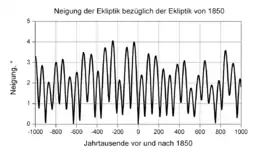
Langzeitverhalten der Neigung der Erdbahn bezüglich der Ekliptik von 1850, aufgetragen über zwei Millionen Jahre.

Die Erdbahnebene ändert aufgrund der Störungen langsam ihre Lage im Raum. Üblicherweise wird diese Ebene selbst als Referenz für Bahnneigungen im Sonnensystem verwendet, die aktuelle Neigung der Erdbahnebene, bezogen auf die aktuelle Erdbahnebene (also auf sich selbst), wäre damit aber stets Null. Die Neigung kann stattdessen sinnvoll bezüglich einer fixen Erdbahn, nämlich der Erdbahn zu einem bestimmten geeignet gewählten Zeitpunkt, angegeben werden.

So schneidet die aktuelle Erdbahn jene Erdbahn, wie sie zum Zeitpunkt J2000.0 lag, entlang einer Schnittgeraden (der „Knotenlinie“), welche in Richtung der ekliptikalen Länge 174,8° gerichtet ist. Sie rotiert langsam um diese Schnittgerade mit einer Rate von 47 Bogensekunden pro Jahrhundert, während die Schnittgerade selbst mit einer Geschwindigkeit von −0,241 Grad pro Jahrhundert entlang der fixen Erdbahnebene wandert.[17]

Das nebenstehende Diagramm zeigt die zeitlich veränderliche Neigung der Erdbahn bezüglich der Erdbahn des Jahres 1850. Diese Neigung erreichte ihr letztes Maximum von 4° 00' um das Jahr 38300 v. Chr. und wird ihr nächstes Maximum von 2° 23' um das Jahr 34100 n. Chr. erreichen.[12]

Im Jahre 1850 fiel die wandernde Erdbahn mit der Erdbahn von 1850 zusammen (definitionsgemäß), so dass die Neigung kurzzeitig den Wert Null annahm. Ein ähnliches Zusammenfallen der wandernden Ebene mit der 1850er Referenzebene war etwa um das Jahr 628000 v. Chr. zu beobachten.[17]

Invariable Ebene als Referenz

Eine andere mögliche Referenzebene ist die „invariable Ebene“ des Sonnensystems, also jene Ebene, welche senkrecht auf dem Gesamtdrehimpuls-Vektor des Sonnensystems steht. Der Drehimpuls ist eine Erhaltungsgröße, der Gesamtdrehimpuls des Sonnensystems kann also nur durch Einwirkung eines Drehmomentes von außen geändert werden. Das Gravitationsfeld der Galaxis übt auf das Sonnensystem nur ein vernachlässigbares Drehmoment aus,[18] daher kann die Ausrichtung des Gesamtdrehimpuls-Vektors und damit die Ausrichtung der auf ihm senkrecht stehenden Ebene praktisch als konstant angesehen werden. Für diese Ausrichtung gilt:

Nördlicher Pol der invariablen Ebene: RA(J2000,0) = 273,8527°, Dek.(J2000,0) = 66,9911° (ein Punkt im Sternbild Drache).[19]

Der Pol der Ekliptik präzediert unter dem Einfluss der Störungen um den Pol der invariablen Ebene. Im Zeitraum von 500000 Jahren vor bis 500000 Jahren nach dem Jahr 2000 umkreist der Ekliptik-Pol den invariablen Pol vierzehnmal, wobei der Abstand der beiden Pole (d. h. die Neigung der beiden Ebenen zueinander) zwischen fast Null und knapp 3 Grad schwankt.[20] Zum Zeitpunkt J2000.0 waren Ekliptik und invariable Ebene um 1,5787° gegeneinander geneigt, die ekliptikale Länge des aufsteigenden Knotens der invariablen Ebene auf der Ekliptik betrug 107,5822°.[21]

Präzession

Die durch die zeitliche Veränderlichkeit von Neigung und Knotenlinie beschriebene Bewegung der Ekliptikebene wird als „planetare Präzession“,[22] neuerdings auch als „Präzession der Ekliptik“[23] bezeichnet. Wäre der Himmelsäquator unbeweglich, so würde die Präzession der Ekliptik alleine zu einer Wanderung des Frühlingspunktes von etwa 12″ pro Jahrhundert und einer Abnahme der Ekliptikschiefe von etwa 47″ pro Jahrhundert führen.[22] Aufgrund der Einwirkung von Sonne und Mond auf den Erdkörper bewegt sich der Äquator jedoch ebenfalls („lunisolare Präzession“,[22] neuerdings auch als „Präzession des Äquators“[23] bezeichnet). Die daraus folgende Bewegung des Frühlingspunktes als Schnittpunkt von Ekliptik und Äquator ist die „allgemeine Präzession“. Sie beträgt gut 5000″ pro Jahrhundert, was also größtenteils auf die Bewegung des Äquators zurückzuführen ist.

Störungen in Länge

Die Gravitationswirkung der anderen Planeten führt nicht nur zu Änderungen in Form und Lage der Erdbahn, sie kann auch die Position des Erde-Mond-Systems auf der Bahn beeinflussen, indem sie dessen Bewegung geringfügig beschleunigt oder verzögert.

Die durch die Venus bewirkte Änderung der ekliptikalen Länge des Erde-Mond-Systems gegenüber dem ungestörten Mittelwert bleibt allerdings stets kleiner als 12 Bogensekunden (″), diejenige durch Mars kleiner als 5″, die durch Jupiter unter 13″ und die durch Saturn unter 1″. Der Einfluss der übrigen Planeten ist noch geringer. Die Störung in ekliptikaler Länge bleibt also insgesamt stets kleiner als etwa 31″. Diese Strecke legt das Erde-Mond-System mit seiner Geschwindigkeit von etwa einem Grad pro Tag in einer knappen Viertelstunde zurück.[24] Um diesen Zeitbetrag kann also der Zeitpunkt, in dem das Erde-Mond-System einen bestimmten Bahnpunkt (z. B. den Frühlingspunkt) durchläuft, aufgrund der Störungen vom mittleren, ungestörten Zeitpunkt abweichen.

Der Umstand, dass es eigentlich der Schwerpunkt des Erde-Mond-Systems ist, welcher der Keplerbahn folgt, während die Erde ihrerseits diesen Schwerpunkt umkreist, kann als eine durch die Anwesenheit des Mondes verursachte Bahnstörung der Erde aufgefasst werden. Der Abstand zwischen dem Erdmittelpunkt und dem Erde-Mond-Schwerpunkt beträgt (bei größtmöglichem Abstand zwischen Erde und Mond) etwa 4942 km.[24] Um diesen Abstand kann der Erdmittelpunkt dem gleichmäßig wandernden Schwerpunkt maximal voraus- oder hinterherlaufen. Bei einer Bahngeschwindigkeit von etwa 30 km/s werden knapp drei Minuten benötigt, um jene Distanz zurückzulegen. Um diesen Zeitbetrag können also die Zeitpunkte, in denen der Erdmittelpunkt bzw. der Erde-Mond-Schwerpunkt einen bestimmten Bahnpunkt (z. B. den Frühlingspunkt) durchlaufen, voneinander abweichen.

Die Zeitpunkte, in denen der Erdmittelpunkt das Perihel oder Aphel durchläuft, können hingegen wie bereits erwähnt um mehrere Tage vom Mittelwert abweichen. Hierfür verantwortlich ist nicht eine Störung in ekliptikaler Länge, sondern die Wellenbewegung des Erdmittelpunkts um den Erde-Mond-Schwerpunkt. Sie kann je nach der in Apsidennähe herrschenden Mondphase den Erdmittelpunkt an deutlich unterschiedlichen Bahnpunkten in die jeweils maximale Sonnennähe oder -ferne tragen. Für Einzelheiten siehe den Artikel → Apsis

Große Halbachse

Die große Halbachse der Erdbahn weist im Gegensatz zu den anderen Bahnelementen nur geringe Schwankungen und keine längerfristige Drift auf. Eine langfristige Berechnung der Planetenbahnen über je 250 Millionen Jahre in die Vergangenheit und in die Zukunft zeigt nur Schwankungen der großen Halbachse zwischen etwa 0,99997 und 1,00003 Astronomischen Einheiten, bei konstant bleibendem Mittelwert.[25]

Umlaufdauer

Die Umlaufdauer (oder Revolutionsperiode) der Erde um die Sonne wird als ein Jahr bezeichnet. Für einen Umlauf benötigt die Erde etwa 365¼ Tage, wie sich aus dem dritten Keplerschen Gesetz für eine ungestörte Ellipsenbahn unter Zuhilfenahme des Gravitationsgesetzes ergibt (zur Bedeutung der Formelzeichen siehe den Artikel →Keplersche Gesetze):

T={\sqrt {\frac {a^{3}4\pi ^{2}}{G(M+m)}}}\approx {\sqrt {\frac {(1{,}496\cdot 10^{11}~{\rm {m}})^{3}\cdot 4\cdot \pi ^{2}}{6{,}67\cdot 10^{-11}\mathrm {\frac {m^{3}}{kg\,s^{2}}} \cdot 1{,}99\cdot 10^{30}~{\rm {kg}}}}}\approx 3{,}156\cdot 10^{7}~{\rm {s}}\approx 365{,}2~{\rm {Tage}}

Da jedoch der Frühlingspunkt wegen der Präzession der Erdachse beweglich ist und die Erdbahn selbst ebenfalls Störungen unterliegt, kann die Bewegung der Erde unter Bezug auf verschiedene zueinander bewegte Bezugspunkte betrachtet werden. Je nachdem, welcher Bezugspunkt gewählt wird, ergeben sich unterschiedliche Zahlenwerte für die Länge des Jahres.

Nach einem siderischen Jahr nimmt die Erde wieder dieselbe Stellung bezüglich eines (unendlich weit entfernt und ohne Eigenbewegung gedachten) Fixsterns ein. Die Länge des siderischen Jahres beträgt etwa 365,256 Tage.
Meteorströme beispielsweise schneiden die Erdbahn immer an derselben Stelle, sofern sie nicht gestört werden. Der zugehörige Sternschnuppenschauer wiederholt sich daher mit der Periode eines siderischen Jahres. Der Unterschied zwischen dem siderischen Jahr und dem tropischen Jahr, nach dem sich der Kalender richtet, beträgt 0,01417 Tage, so dass der Durchgang der Erde durch den betreffenden Bahnpunkt alle 70,6 Jahre um einen Tag später im Kalender liegt. Die Perseiden sind ein Beispiel für einen wenig gestörten Schauer. Sie treten gegenwärtig um den 12. August herum auf, wurden aber Mitte des 19. Jahrhunderts um den 10. August, zur ersten Jahrtausendwende am Ende des Juli und zu Beginn unserer Zeitrechnung etwa Mitte Juli beobachtet.[26][Anm. 5]
Nach einem tropischen Jahr nimmt die Erde wieder dieselbe Stellung bezüglich des Frühlingspunkts ein. Da der Frühlingspunkt der Erde entgegenläuft (siehe Abschnitt →Jahreszeiten), ist das tropische Jahr etwas kürzer als das siderische und hat eine Dauer von etwa 365,242 Tagen.
Mit der Periode des tropischen Jahres wiederholen sich die Jahreszeiten. Solar- und Lunisolarkalender versuchen daher mittels geeigneter Schaltregeln, die Länge ihrer Kalenderjahre im Mittel an das tropische Jahr anzupassen. Für eine Reihe genauerer aber etwas unterschiedlicher Definitionen des tropischen Jahres und die damit verbundenen verschiedenen Zahlenwerte siehe tropisches Jahr.
Nach einem anomalistischen Jahr nimmt die Erde wieder dieselbe Stellung bezüglich ihres Perihels ein. Da sich das Perihel rechtläufig entlang der Bahn bewegt, ist das anomalistische Jahr etwas länger als das siderische Jahr und hat eine Dauer von etwa 365,260 Tagen.
Nach einem Finsternisjahr liegen Sonne, Mond und die beiden Knoten der Mondbahn wieder in einer Linie. Damit ist eine der Bedingungen für eine Sonnen- oder Mondfinsternis gegeben. Eine Finsternis ergibt sich, wenn in hinreichender zeitlicher Nähe zu dieser Konfiguration als zweite Bedingung ein Neu- oder Vollmond eintritt. Da die erforderliche „Nähe“ einen Zeitraum von gut einem Monat umfasst und sich in diesem Zeitraum zwei bis drei Neu- und Vollmonde ereignen, treten stets mehrere Finsternisse kurz hintereinander als Gruppe (M-S, S-M, M-S-M oder S-M-S)[27] auf. Ein halbes Finsternisjahr später folgt (am anderen Mondknoten) die nächste Finsternisgruppe. Da die Mondknoten wegen der Präzession der Mondbahn während eines Jahres um etwa 19° rückläufig wandern, kommen sie dem Erdumlauf entgegen, so dass bereits nach (im Mittel) 346,620 Tagen erneut Finsternisse am selben Knoten stattfinden können. Im Jahre 2015 beispielsweise liegt die erste so genannte „Finsternis-Saison“ im März/April (S-M) und die zweite im September (S-M). Bis zum Jahre 2018 haben sich die Finsternis-Saisons bereits auf Januar/Februar (M-S) bzw. Juli/August (S-M-S) vorverschoben.

Die mittlere Länge der genannten Jahre beträgt (für die Epoche 2012,0):[28]

Siderisches Jahr:	Rückkehr zum selben Stern,	365^d	6^h	9^m	9,8^s	oder	365,256 363 Tage
Tropisches Jahr:	Rückkehr zum Frühlingspunkt,	365^d	5^h	48^m	45,2^s	oder	365,242 190 Tage
Anomalistisches Jahr:	Rückkehr zum Perihel,	365^d	6^h	13^m	52,6^s	oder	365,259 636 Tage
Finsternisjahr:	Rückkehr zum selben Mondknoten	346^d	14^h	52^m	54,9^s	oder	346,620 080 Tage

Individuelle Jahre können aufgrund von Störungen von diesen Mittelwerten abweichen. Darüber hinaus unterliegen die mittleren Jahreslängen aufgrund langfristiger Veränderungen der Erdbahn einer langsamen Drift.

Jahreszeiten

Die vier Jahreszeiten

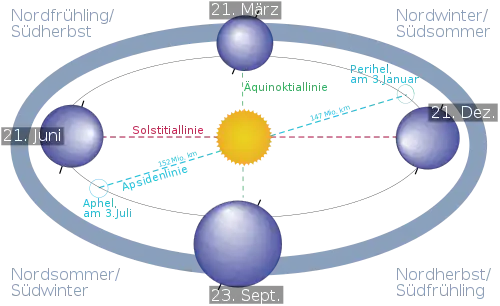
Zu Frühlingsbeginn befindet sich die Erde definitionsgemäß auf der ekliptikalen Länge 180°. Von der Erde aus gesehen befindet sich die Sonne dann auf 0° (dem Frühlingspunkt), während die um Mitternacht sichtbaren Sternbilder in der gegenüberliegenden Richtung bei 180° liegen. Dies sind gegenwärtig insbesondere die Sternbilder in der Umgebung von Löwe und Jungfrau – typische Frühlingssternbilder. Im Sommer sind um Mitternacht die um die ekliptikale Länge 270° herum liegenden Sternbilder sichtbar, insbesondere also die Sommersternbilder um den Schützen herum. Die Mitternacht im Herbst präsentiert als Herbststernbilder unter anderem die bei einer Länge von 0° gelegenen Fische. Um Mitternacht im Winter steht die ekliptikale Länge 90° am Himmel und mit ihr die Zwillinge und andere Wintersternbilder. (Hinreichend nahe am Himmelspol gelegene Sternbilder wie z. B. der Große Bär sind zirkumpolar und daher in allen Jahreszeiten sichtbar.)

Da aufgrund des Gravitationseinflusses von Mond, Sonne und Planeten weder die Äquator- noch die Ekliptikebene fix im Raum stehen, sind die Schiefe der Ekliptik als Schnittwinkel beider Ebenen und insbesondere die Lage des Frühlingspunkts auf der Schnittlinie beider Ebenen zeitlich veränderlich. Die Schiefe der Ekliptik schwankt mit einer Periode von etwa 40.000 Jahren und mit einer Amplitude von etwa 1° um einen Mittelwert von etwa 23°. Der Frühlingspunkt präzediert in knapp 26.000 Jahren einmal bezüglich des Fixsternhintergrunds rund um die Erdbahn, und zwar in der dem Erdumlauf entgegengesetzten Richtung (rückläufig).

Aus der Drift des Frühlingspunktes entlang der Erdbahn folgt, dass künftig die Jahreszeiten mit anderen Abschnitten der Erdbahn zusammenfallen werden. Nach einem Viertel der Präzessionsperiode, also in etwa 6500 Jahren, wird der Sommer auf den Bahnabschnitt fallen, in dem jetzt Frühling herrscht, und entsprechend werden die von diesem Bahnabschnitt aus sichtbaren jetzigen „Frühlings“sternbilder zu „Sommer“sternbildern geworden sein.

Die erwähnten Veränderungen von Exzentrizität, Ekliptikschiefe und Lage des Frühlingspunkts führen in ihrem Zusammenwirken periodenweise zu stärkeren oder schwächeren Ausprägungen der Jahreszeiten und sind daher vermutlich eine der Ursachen für den Wechsel von Warm- und Eiszeiten (siehe auch: →Milanković-Zyklen). Dabei ist nicht die Lage des Frühlingspunkts bezüglich des Fixsternhintergrunds von Bedeutung, sondern seine Lage bezüglich des Perihels (zur Begründung siehe den Artikel →Jahreszeiten). Da das Perihel rechtläufig um die Erdbahn wandert (siehe Abschnitt →Perihel), trifft der rückläufige Frühlingspunkt bereits wieder mit ihm zusammen, bevor er einen vollen Umlauf bezüglich der Fixsterne vollendet hat. Die gegenseitigen Stellungen von Frühlingspunkt und Perihel wiederholen sich daher mit der bereits erwähnten „klimatischen“ Periode von nur etwa 21.000 Jahren.

Langzeitstabilität

„Chaos“

Berechnet man die Bewegung der Planeten unter dem Gravitationseinfluss der Sonne und der jeweils anderen Planeten über lange Zeiträume, so stellt man fest, dass das äußere Sonnensystem im Wesentlichen stabil, das innere Sonnensystem (Merkur, Venus, Erde, Mars) jedoch schwach chaotisch (im mathematischen Sinne) ist.[29] Das bedeutet nicht, dass die Planeten irgendwann beginnen, regellos (also im umgangssprachlichen Sinne „chaotisch“) durcheinanderzulaufen. Es bedeutet lediglich, dass kleine Unsicherheiten in den Startbedingungen einer Langzeitrechnung sich aufgrund der komplexen gravitativen Wechselwirkungen zwischen den Planeten aufschaukeln und schließlich der Vorhersagbarkeit Grenzen setzen. Eine Unsicherheit von beispielsweise 15 Metern in der Startposition der Erde führt nach 10 Millionen Jahren zu einer Unsicherheit von etwa 150 Metern und nach 100 Millionen Jahren zu einer Unsicherheit von etwa 150 Millionen Kilometern.[29]

Es ist daher durchaus möglich, eine präzise Ephemeride der Erde über einige zehn Millionen Jahre hinweg zu berechnen. Über längere Zeiträume jedoch werden die berechneten Positionen zunehmend unsicher, und nach spätestens hundert Millionen Jahren erreicht die Unsicherheit die Abmessungen der Erdbahn selbst – es ist dann nicht mehr möglich vorherzusagen, an welchem Punkt ihrer Bahn sich die Erde befindet. Auch dies bedeutet nicht, dass die Erde sich dann regellos irgendwo im inneren Sonnensystem befinden wird. Sie wird sich nach wie vor auf ihrer gewohnten Bahn befinden, und die Bahn selbst wird sich nur geringfügig im Rahmen der oben erwähnten Störungen von der heutigen Bahn unterscheiden. Lediglich der Ort der Erde auf dieser Bahn ist von heute aus nicht mehr vorhersagbar.

Stabilität

Die Stabilität des Sonnensystems wäre beeinträchtigt, wenn die beschriebenen Formänderungen der Planetenbahnen – insbesondere eine eventuelle starke Zunahme der Exzentrizitäten – langfristig zu engen Annäherungen benachbarter Bahnen führen könnten. Ein Planet könnte dann mit einem Nachbarplaneten kollidieren oder bei einer zu nahen Begegnung aus seiner Bahn oder gar aus dem Sonnensystem geschleudert werden.

Wie die oben erwähnten Langzeitrechnungen zeigen, können solche Instabilitäten für die nächsten hundert Millionen Jahre ausgeschlossen werden. Für den Rest der erwarteten Lebensdauer des Sonnensystems von etwa 5 Milliarden Jahren müssen andere Untersuchungsmethoden verwendet werden. Ein einzelner Rechenlauf kann wegen der anwachsenden Unsicherheit jenseits von 100 Millionen Jahren zwar nicht als konkrete Vorhersage angesehen werden, er stellt jedoch eine mögliche Entwicklung dar. Die Analyse eines Ensembles von Bahnen (d. h. von zahlreichen Rechenläufen mit leicht unterschiedlichen Startbedingungen) ermöglicht statistische Abschätzungen von typischen oder zumindest möglichen Szenarien.

Die Rechnungen vereinfachen sich, wenn man die Planeten selbst unberücksichtigt lässt und Formeln für die zeitliche Entwicklung der Bahnen aufstellt.[30] Die langsamen Bahnänderungen erfordern einen geringeren Rechenaufwand als die rasch veränderlichen Positionen der Planeten in der Bahn, so dass ein ganzes Bahn-Ensemble leichter rechentechnisch bewältigt werden kann. Entsprechende Untersuchungen zeigten, dass über mehrere Milliarden Jahre hinweg die Exzentrizität der Erdbahn ihren gegenwärtigen Maximalwert von ca. 0,06 nur geringfügig überschreitet und die Bahn der Venus sich ähnlich verhält. Die Exzentrizität des Mars schwankt stärker, eine allzu nahe Begegnung der Erde mit Mars oder Venus ist jedoch nicht zu erwarten. Merkur dagegen zeigt starke Schwankungen der Exzentrizität, so dass nahe Begegnungen mit der Venus nicht grundsätzlich ausgeschlossen werden können.[30]

Mittlerweile ist es möglich geworden, auf Großrechnern die vollständigen Planetenbewegungen über mehrere Milliarden Jahre hinweg zu berechnen. Eine Untersuchung mit insgesamt 2501 jeweils 5 Milliarden Jahre umspannenden Rechenläufen zeigte in der weit überwiegenden Zahl der Fälle dasselbe Bild wie im heutigen Sonnensystem: die Planetenbahnen verformen sich periodisch und präzedieren unter ihren gegenseitigen Wechselwirkungen, jedoch ohne die Gefahr von Nahbegegnungen. In einem Prozent der Fälle stieg die Exzentrizität des Merkur erheblich an, was dann oft zur Kollision mit der Venus oder der Sonne führte, ohne jedoch die Erdbahn merklich zu beeinträchtigen. Lediglich in einem der 2501 Fälle verursachte nach mehreren Milliarden Jahren eine stark exzentrische Merkurbahn eine ebenfalls stark ansteigende Exzentrizität der Marsbahn, welche dann – je nach Einzelheiten des betrachteten Szenarios – eine Kollision der Erde mit einem der Nachbarplaneten ermöglichte.[31] Die statistischen Details sind nicht unumstritten.[32]

Insgesamt kann das Sonnensystem als „marginal stabil“ betrachtet werden: Erhebliche Instabilitäten (wie z. B. eine Kollision) können nicht grundsätzlich ausgeschlossen werden, sind aber allenfalls über Zeiträume von mehreren Milliarden Jahren hinweg zu erwarten.[33] Für die Bahnen von Erde und Venus sind wegen der relativ großen Planetenmassen und ihrer gegenseitigen Kopplung nur geringe Abweichungen von ihrer heutigen Gestalt zu erwarten. Sie können während der Lebensdauer des Sonnensystems als in sich stabil angesehen werden, sofern sie nicht durch größere Instabilitäten anderer Planetenbahnen in Mitleidenschaft gezogen werden.[33]

Sonnenbahn

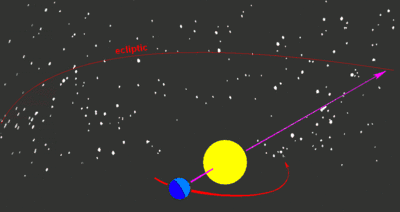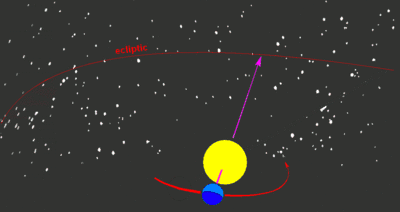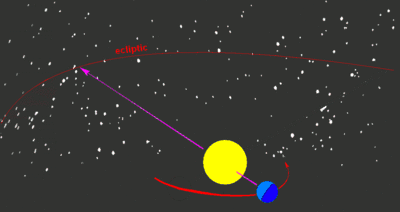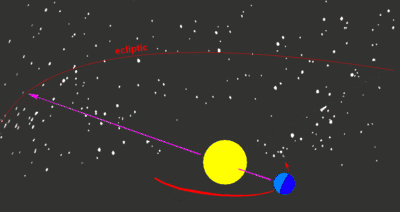
Die Sonne scheint sich gegenüber den Hintergrundsternen zu bewegen. Tatsächlich bewegt sich die Erde so, dass sich der Blickwinkel ändert, unter dem die Sonne vor dem Hintergrund gesehen wird.

Aus irdischer Sicht scheint die Sonne im Laufe eines Jahres die Sternbilder der Ekliptik zu durchwandern, nach denen auch die zwölf Tierkreiszeichen benannt sind. Diese Bewegung der Sonne um die Erde bezeichnet man als scheinbare geozentrische Bahn.

Zur scheinbaren topozentrischen Bahn der Sonne, dem von einem realen Beobachter auf der Erde wahrgenommenen Anblick am Himmel, siehe: Sonnenstand

In der himmelsmechanischen Darstellung ist der geozentrische Ortsvektor der Sonne dem heliozentrischen Ortsvektor der Erde genau entgegengesetzt, daher kann in Berechnungen derselbe Formelsatz verwendet werden. Dieser wird im Artikel →Sonnenstand ausführlich erläutert.

Bei astronomischen Führungen macht es den Teilnehmern oft Probleme, sich die räumliche Lage der Ekliptik vorzustellen. Denn wegen der Ekliptikschiefe von etwa 23,5° verändert sich z. B. ihr Schnitt mit dem östlichen Horizont – der Richtung des Sonnenaufgangs – je nach Jahreszeit von etwa Nordost bis Südost. Zur Stützung dieser Vorstellung wurden u. a. Geräte wie die Armillarsphäre und die Ekliptikscheibe entwickelt.

Bahnelemente

Die in der Infobox dieses Artikels tabellierten Bahnelemente entsprechen dem aktuellen Stand der Astronomie. Sie stellen jedoch aus Platzgründen nur die mittleren Werte dar und sind nur für den Zeitpunkt J2000.0 gültig, so dass sie für Berechnungen der Erdbahn von sehr eingeschränktem Nutzen sind. Eine vollständige Darstellung des entsprechenden Datensatzes inklusive der Bahnstörungen und der zeitlichen Abhängigkeiten ist wegen seines Umfangs hier nicht möglich. Für die meisten praktischen Anwendungen genügen jedoch stark vereinfachte Rechenverfahren.

Da sich die Erdbahn in guter Näherung durch eine Kepler-Ellipse beschreiben lässt, können die Elemente einer solchen Ellipse näherungsweise für die Berechnung der Position der Erde zu einem gegebenen Zeitpunkt benutzt werden. Die Abweichungen der Erdbahn von einer exakten Ellipse können dabei auf verschiedene Weise zum Teil berücksichtigt werden.

Mittlere Kepler-Elemente

Die folgenden Kepler-Elemente sind „mittlere“ Elemente, d. h. die periodischen Bahnstörungen sind nicht berücksichtigt. Diejenigen Anteile der Störungen sind jedoch berücksichtigt, die durch eine lineare zeitliche Variation der mittleren Elemente beschrieben werden können. Höhere Potenzen der zeitlichen Variation sind ebenfalls vernachlässigt. Sobald die mittleren Elemente für den gewünschten Zeitpunkt aus den folgenden Tabellen ermittelt wurden, können die üblichen Standardverfahren zur Berechnung der Planetenposition aus gegebenen Kepler-Elementen verwendet werden.

Der folgende Satz mittlerer Keplerelemente[34] liefert die Position des Erde-Mond-Schwerpunktes in Bezug auf das Äquinoktium des Datums:

a	= 1,000000	AE	große Halbachse
ε	= 0,016709 − 0,000042·T		Numerische Exzentrizität
i	= 0,0	°	Bahnneigung, bezogen auf die Ekliptik des Datums
Ω	nicht definiert		Länge des aufsteigenden Knotens (Äquinoktium des Datums)
ϖ	= 102,9400 + 1,7192·T	°	Länge des Perihels (Äquinoktium des Datums)
M	= 357,5256 + 35999,0498·T	°	mittlere Anomalie
L	= 100,4656 + 36000,7690·T	°	mittlere Länge (Äquinoktium des Datums), L = M + ϖ

Soll die Position bezüglich des Äquinoktiums J2000.0 berechnet werden, so sind die davon abhängigen Elemente wie folgt zu ersetzen:[34][Anm. 6]

i₀	= 0,0 + 0,0131·T	°	Bahnneigung, bezogen auf die Ekliptik von J2000.0
Ω₀	= 174,876 − 0,242·T	°	Länge des aufsteigenden Knotens (Äquinoktium J2000.0)
ϖ₀	= 102,9400 + 0,3222·T	°	Länge des Perihels (Äquinoktium J2000.0)
L₀	= 100,4656 + 35999,3720·T	°	mittlere Länge (Äquinoktium J2000.0), L₀ = M + ϖ₀

Die Zeit T ist in Julianischen Jahrhunderten seit dem 1. Januar 2000, 12^h TT zu messen, für eine Julianische Tageszahl JD ist also T = (JD-2451545.0)/36525.

Angepasste Kepler-Elemente

Eine andere Möglichkeit, die Erdbahn inklusive eines Teiles der Störungen genähert durch Kepler-Elemente darzustellen, besteht darin, nicht die mittleren Bahnelemente zu ermitteln, sondern jene Elemente, welche die mittleren Bahnen beschreiben (aufgrund des nichtlinearen Zusammenhangs zwischen Bahnelementen und Bahn ist das nicht dasselbe). Die folgenden Kepler-Elemente wurden so gewählt, dass die aus ihnen folgenden Bahnen über einen bestimmten Zeitraum im Mittel möglichst gut mit der tatsächlichen Bahn übereinstimmen.

Kepler-Elemente für genäherte Positionen des Erde-Mond-Schwerpunkts, bezogen auf die mittlere Ekliptik und das Äquinoktium für J2000.0:[35]

1800 – 2050:
a	=	1,000 002 61	+	0,000 005 62 · T	AE
ε	=	0,016 711 23	−	0,000 043 92 · T	rad
i	=	−0,000 015 31	−	0,012 946 68 · T	°
L	=	100,464 571 66	+	35999,372 449 81 · T	°
ϖ	=	102,937 681 93	+	0,323 273 64 · T	°
Ω	=	0,000 000 00	+	0,000 000 00 · T	°

Die mit diesen Elementen berechneten Positionen weisen während des angegebenen Zeitraums 1800–2050 Fehler der folgenden Größenordnungen auf: Rektaszension 20", Deklination 8", Radiusvektor 6000 km.[35] Außerhalb dieses Zeitraums sollten die Elemente nicht benutzt werden.

3000 v. Chr. – 3000 n. Chr.:
a	=	1,000 000 18	−	0,000 000 03 · T	AE
ε	=	0,016 731 63	−	0,000 036 61 · T	rad
i	=	−0,000 543 46	−	0,013 371 78 · T	°
L	=	100,466 915 72	+	35999,373 063 29 · T	°
ϖ	=	102,930 058 85	+	0,317 952 60 · T	°
Ω	=	−5,112 603 89	−	0,241 238 56 · T	°

Die mit diesen Elementen berechneten Positionen weisen während des angegebenen Zeitraums 3000 v. Chr. – 3000 n. Chr. Fehler der folgenden Größenordnungen auf: Rektaszension 40", Deklination 15", Radiusvektor 15000 km.[35] Außerhalb dieses Zeitraums sollten die Elemente nicht benutzt werden.

Die Zeit T ist in Julianischen Jahrhunderten seit dem 1. Januar 2000, 12^h TT zu messen, für eine Julianische Tageszahl JD ist also T = (JD-2451545.0)/36525.

Andere Bahndarstellungen

Sollen die Störungen vollständig berücksichtigt, die Bahn aber nach wie vor durch Kepler-Elemente dargestellt werden, so können oskulierende Kepler-Elemente verwendet werden, die jene Kepler-Ellipse beschreiben, welche sich der realen, gestörten Bahn am momentanen Ort des Planeten am besten anschmiegt. Die oskulierenden Elemente sind wegen der Störungen relativ rasch veränderlich und müssen daher auf einem entsprechend feinen Zeitraster tabelliert werden. Der Astronomical Almanac enthält auf Seite E7 die oskulierenden Erdbahnelemente für das jeweilige Jahr auf einem 40-Tage-Raster.

Statt durch Kepler-Elemente kann eine Planetenbahn auch durch Reihenentwicklungen für Länge, Breite und Radiusvektor dargestellt werden. Die Störungen können durch Hinzufügen geeigneter Terme berücksichtigt werden. Genaue Bahndarstellungen können viele tausend Terme enthalten, bei geringeren Genauigkeitsansprüchen kann die Berechnung jedoch abgebrochen werden, sobald die gewünschte Genauigkeit erreicht ist. Die für Alltagsansprüche gedachte kurze Reihenentwicklung nach van Flandern und Pulkkinen[36] erzielt über den Zeitraum von etwa 300 Jahren vor bis 300 Jahre nach der Gegenwart eine Genauigkeit von etwa einer Bogenminute. Aufwändigere Reihenentwicklungen sind z. B. die VSOP87 und die VSOP2013.

Die genaueste Berechnung von Ephemeriden wird durch numerisches Lösen der Bewegungsgleichungen erzielt. Das Ergebnis ist eine Tabelle mit tabellierten Planetenpositionen, aus denen der Benutzer die Position für den gewünschten Zeitpunkt auslesen kann. Beispiele sind die verschiedenen „Development Ephemeris“ DExxx [37][38] des JPL, die „Integration Numerique Planetaire de l’Observatoire de Paris“ INPOP [39] des IMCCE, oder die „Ephemerides of Planets and the Moon“ EPM [40] des Instituts für angewandte Astronomie der Russischen Akademie der Wissenschaften.

Koorbitale Objekte

Die Erde wird auf ihrer Bahn um die Sonne von einigen koorbitalen Objekten begleitet. Diese kleinen Himmelskörper umkreisen die Sonne auf Bahnen, auf denen sie eine ähnliche oder gar dieselbe Umlaufdauer haben wie die Erde. Aufgrund der geringen Relativgeschwindigkeit und mit Hilfe von Resonanzeffekten kann die Anziehungskraft der Erde diese Objekte mehr oder weniger dauerhaft in ihren koorbitalen Bahnen halten.

So lenkt die Erde den erdnahen Asteroiden Cruithne auf eine Hufeisenumlaufbahn entlang der Erdbahn. Der Asteroid 2003 YN₁₀₇ war in den Jahren von 1996 bis 2006 ein Quasisatellit der Erde und wird bei der übernächsten Begegnung im Jahr 2120 möglicherweise als wirklicher zweiter Mond von der Erde eingefangen werden. Der koorbitale Asteroid 2002 AA₂₉ wechselt annähernd zyklisch zwischen einer Hufeisenumlaufbahn und einer Quasisatellitenbahn und wird das nächste Mal um das Jahr 2600 wieder für 45 Jahre ein Quasisatellit der Erde sein.

Im Oktober 2010 wurde mit 2010 TK₇ ein weiteres koorbitales Objekt der Erde entdeckt, das im Juli 2011 als erster Trojaner der Erde nachgewiesen werden konnte. Der ca. 300 m große Asteroid kreist auf einer stabilen Bahn um den Lagrange-Punkt L₄ und damit 60° vor der Erde auf ihrer Umlaufbahn um die Sonne.

Siehe auch

Weblinks

Wiktionary: Erdbahn – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

WEBGEO-Modul: Erde, Erdbahn, astronomische Jahreszeiten – WEBGEO – E-Learning-Portal für Geographie und Nachbarwissenschaften

Anmerkungen

Die scheinbare tägliche Wanderung der Sonne über den Himmel ist lediglich auf die Erdrotation zurückzuführen: die Sonne wandert hierbei gemeinsam mit den Fixsternen über den Himmel, und zwar näherungsweise parallel zum Äquator, nicht entlang der Ekliptik.
Wenn die Erde diesen Punkt im Winter durchläuft, sieht sie die Sonne am gegenüberliegenden Punkt im Sternbild Schütze stehen
Die in der Quelle in Bogensekunden angeführten Koeffizienten von t wurden hier der besseren Lesbarkeit wegen durch Division mit 3600 in Grad umgerechnet.
Das Formelzeichen ϖ ist kein ω (omega) mit einer Tilde, sondern ein kursives π (pi).
Der Vergleichbarkeit halber wurden die vor der Gregorianischen Kalenderreform liegenden Angaben auf einen fiktiven proleptischen Gregorianischen Kalender umgerechnet.
Für T<0 bezeichnen i₀ die negative Bahnneigung und Ω₀ den absteigenden Knoten. Dies vermeidet den eigentlich vorhandenen aber rechnerisch unpraktischen Sprung in Ω₀, wenn die aktuelle Ekliptik die Ekliptik von J2000.0 durchdringt.

Einzelnachweise

J. L. Simon, P. Bretagnon, J. Chapront, M. Chapront-Touzé, G. Francou, J. Laskar: Numerical expressions for precession formulae and mean elements for the Moon and the planets. In: Astronomy and Astrophysics. vol. 282, 1994, S. 663–683. (online)
IMCCE: Le manuel des éclipses. EDP Sciences, Les Ulis 2005, ISBN 2-86883-810-3, S. 27: Mittlere Bahnelemente der Erde zur Epoche J2000. (online)
A. Lehnen, J. Kessenich: Moments of the Distance from the Force Center in a Two-Body Kepler Orbit. Tabelle 4 (online, abgerufen am 20. Januar 2015)
NASA: Earth Fact Sheet (aufgerufen am 19. November 2014)
Perihelabstand = a·(1 - e), Aphelabstand = a·(1 + e).
J. B. Tatum: Celestial Mechanics Kap. 9 (PDF 203 kB): <r> = a·(1 + 1/2 e²), abgerufen am 9. Januar 2015
J. Meeus: Astronomical Algorithms. 2. Auflage. Willmann-Bell, Richmond 2000, ISBN 0-943396-61-1, Kap. 33: Der Umfang einer Ellipse mit großer Halbachse a und Exzentrizität e ist L = 2π a [ 1 − e²/4 − 3/64 e⁴ − 45/2304 e⁶ − … ]
P. K. Seidelmann (Hrsg.): Explanatory Supplement to the Astronomical Almanac. University Science Books, Mill Valley 1992, ISBN 0-935702-68-7, S. 700.
Markus Mugrauer, Hannes Keppler: Spektroskopische Vermessung der Erdbahn und Bestimmung der Sonnenmasse, Mitteilung der Spektrum der Wissenschaft Verlagsgesellschaft mbH 2018, abgerufen am 29. Dez. 2021
90° minus Schiefe der Ekliptik (23° 26' 21,412" gemäß Simon et al.: Numerical expressions…)
A. N. Cox (Hrsg.): Allen's Astrophysical Quantities. 4. Auflage. Springer Science+Business Media, New York 2004, ISBN 0-387-98746-0, S. 12.
J. Meeus: More Mathematical Astronomy Morsels. Willmann-Bell, Richmond 2002, ISBN 0-943396-74-3, Kap. 33
A. Berger, M. F. Loutre: Precession, Eccentricity, Obliquity, Insolation and Paleoclimates. In: J.-C. Duplessy, M.-T. Spyridakis (Hrsg.): Long-Term Climatic Variations. NATO ASI Series, Band I 22 (1994) S. 107–152 (PDF, 5,1 MB). Der zeitliche Mittelwert von (a/r)² ist $\textstyle \left\langle {\frac {a^{2}}{r^{2}}}\right\rangle \,=\,{\frac {1}{T}}\int _{0}^{T}\left({\frac {a}{r}}\right)^{2}dt\,=\,{\frac {1}{\sqrt {1-\varepsilon ^{2}}}}$ .
J. Meeus: Mathematical Astronomy Morsels. Willmann-Bell, Richmond 1997, ISBN 0-943396-51-4, Kap. 27
Earth at Perihelion and Aphelion: 1501 to 1600 … Earth at Perihelion and Aphelion: 2001 to 2100 … Earth at Perihelion and Aphelion: 2401 to 2500 von Fred Espenak (astropixels.com), abgerufen 8. Juli 2021
Eva Bauer: Klimafaktoren und Klimaänderungen im letzten Jahrtausend. In: Sterne und Weltraum. Dezember 2005, S. 31–38. PDF (932 kB) (Memento vom 4. März 2016 im Internet Archive)
J. Meeus: Astronomical Algorithms. 2. Auflage. Willmann-Bell, Richmond 2000, ISBN 0-943396-61-1, Kap. 31
A. J. J. van Woerkom: Note about galactic precession. In: Bulletin of the Astronomical Institutes of the Netherlands. Band 9, (1943), S. 427 (online)
R. S. Steadly, M. S. Robinson (Hrsg.): The Astronomical Almanac for the Year 2012. U.S. Government Printing Office, ISBN 978-0-7077-4121-5, S. E2.
W. M. Owen, Jr.: A Theory of the Earth's Precession Relative to the Invariable Plane of the Solar System. Dissertation, University of Florida 1990, Abb. 5–1, S. 253 (online)
D. Souami, J. Souchay: The solar system's invariable plane. In: Astronomy & Astrophysics. Band 543, Juli 2012, article nr. A133, doi:10.1051/0004-6361/201219011
P. K. Seidelmann (Hrsg.): Explanatory Supplement to the Astronomical Almanac. University Science Books, Mill Valley 1992, ISBN 0-935702-68-7, S. 99.
S. E. Urban, P. K. Seidelmann (Hrsg.): Explanatory Supplement to the Astronomical Almanac. 3. Auflage. University Science Books, Mill Valley 2013, ISBN 978-1-891389-85-6, S. 212.
J. Meeus: More Mathematical Astronomy Morsels. Willmann-Bell, Richmond 2002, ISBN 0-943396-74-3, Kap. 27
J. Laskar, P. Robutel, F. Joutel, M. Gastineau, A.C.M. Correia, B. Levrard: A long-term numerical solution for the insolation quantities of the Earth. Astronomy & Astrophysics 428, 261–285 (2004), doi:10.1051/0004-6361:20041335, S. 268ff und Fig. 11
D. W. Hughes, B. Emerson: The stability of the node of the Perseid meteor stream. In: The Observatory. Band 102, 1982, S. 39–42. (online)
IMCCE: Le manuel des éclipses. EDP Sciences, Les Ulis 2005, ISBN 2-86883-810-3, S. 85ff.
R. S. Steadly, M. S. Robinson (Hrsg.): The Astronomical Almanac for the Year 2012. U.S. Government Printing Office, ISBN 978-0-7077-4121-5, S. C2.
J. Laskar: Is the Solar System stable? In: Progress in Mathematical Physics. 66, 2013, S. 239–270 (preprint, S. 19)
J. Laskar: Large Scale Chaos and Marginal Stability in the Solar System. In: Celestial Mechanics and Dynamical Astronomy. Band 64, 1996, Heft 1–2, S. 115–162 (online), S. 147ff.
J. Laskar: Is the Solar System stable? In: Progress in Mathematical Physics. 66, 2013, S. 239–270 (preprint, S. 27)
R. E. Zeebe: Dynamic stability of the Solar System: Statistically inconclusive results from ensemble integrations. In: The Astrophysical Journal. accepted (arxiv:1506.07602 preprint)
J. Laskar: Large Scale Chaos and Marginal Stability in the Solar System. In: Celestial Mechanics and Dynamical Astronomy. Band 64, 1996, Heft 1–2, S. 115–162 (online), S. 155.
O. Montenbruck: Grundlagen der Ephemeridenrechnung. 6. Auflage. Verlag Sterne und Weltraum, Heidelberg 2001, ISBN 3-87973-941-2, S. 139.
S. E. Urban, P. K. Seidelmann (Hrsg.): Explanatory Supplement to the Astronomical Almanac. 3. Auflage. University Science Books, Mill Valley 2013, ISBN 978-1-891389-85-6, S. 338 (Kap. 8.10: Keplerian Elements for Approximate Positions of the Major Planets.) (preprint, PDF 68 kB)
T. C. Van Flandern, K. F. Pulkkinen: Low-precision Formulae for Planetary Positions. In: Astrophysical Journal Supplement Series. Band 41 (Nov. 1979) S. 391–411 (online)
Ephemeriden-Dateien auf dem FTP-Server des JPL: (siehe README.txt)
Ephemeriden-Server des JPL zum direkten Abruf von Planetenpositionen: ssd.jpl.nasa.gov
IMCCE: INPOP13c, a 4-D planetary ephemeris (abgerufen am 8. Januar 2015)
E. V. Pitjeva: Updated IAA RAS Planetary Ephemerides-EPM2011 and Their Use in Scientific Research. In: Solar System Research. Band 47, Heft 5, September 2013, S. 386–402. (doi:10.1134/S0038094613040059, preprint)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[10] Die scheinbare tägliche Wanderung der Sonne über den Himmel ist lediglich auf die Erdrotation zurückzuführen: die Sonne wandert hierbei gemeinsam mit den Fixsternen über den Himmel, und zwar näherungsweise parallel zum Äquator, nicht entlang der Ekliptik.

[13] Wenn die Erde diesen Punkt im Winter durchläuft, sieht sie die Sonne am gegenüberliegenden Punkt im Sternbild Schütze stehen

[SekGrad-16] Die in der Quelle in Bogensekunden angeführten Koeffizienten von t wurden hier der besseren Lesbarkeit wegen durch Division mit 3600 in Grad umgerechnet.

[varpi-17] Das Formelzeichen ϖ ist kein ω (omega) mit einer Tilde, sondern ein kursives π (pi).

[31] Der Vergleichbarkeit halber wurden die vor der Gregorianischen Kalenderreform liegenden Angaben auf einen fiktiven proleptischen Gregorianischen Kalender umgerechnet.

[40] Für T<0 bezeichnen i₀ die negative Bahnneigung und Ω₀ den absteigenden Knoten. Dies vermeidet den eigentlich vorhandenen aber rechnerisch unpraktischen Sprung in Ω₀, wenn die aktuelle Ekliptik die Ekliptik von J2000.0 durchdringt.

[SimonEtAl-1] J. L. Simon, P. Bretagnon, J. Chapront, M. Chapront-Touzé, G. Francou, J. Laskar: Numerical expressions for precession formulae and mean elements for the Moon and the planets. In: Astronomy and Astrophysics. vol. 282, 1994, S. 663–683. (online)

[IMCCE1-2] IMCCE: Le manuel des éclipses. EDP Sciences, Les Ulis 2005, ISBN 2-86883-810-3, S. 27: Mittlere Bahnelemente der Erde zur Epoche J2000. (online)

[Lehnen_Kessenich_Tab4-3] A. Lehnen, J. Kessenich: Moments of the Distance from the Force Center in a Two-Body Kepler Orbit. Tabelle 4 (online, abgerufen am 20. Januar 2015)

[NASAEarthFactSheet-4] NASA: Earth Fact Sheet (aufgerufen am 19. November 2014)

[Perihel_Aphel-5] Perihelabstand = a·(1 - e), Aphelabstand = a·(1 + e).

[Tatum_CelMechs_9.11-6] J. B. Tatum: Celestial Mechanics Kap. 9 (PDF 203 kB): <r> = a·(1 + 1/2 e²), abgerufen am 9. Januar 2015

[MeeusAstrAlgKap33-7] J. Meeus: Astronomical Algorithms. 2. Auflage. Willmann-Bell, Richmond 2000, ISBN 0-943396-61-1, Kap. 33: Der Umfang einer Ellipse mit großer Halbachse a und Exzentrizität e ist L = 2π a [ 1 − e²/4 − 3/64 e⁴ − 45/2304 e⁶ − … ]

[ExplSuppl_S700-8] P. K. Seidelmann (Hrsg.): Explanatory Supplement to the Astronomical Almanac. University Science Books, Mill Valley 1992, ISBN 0-935702-68-7, S. 700.

[9] Markus Mugrauer, Hannes Keppler: Spektroskopische Vermessung der Erdbahn und Bestimmung der Sonnenmasse, Mitteilung der Spektrum der Wissenschaft Verlagsgesellschaft mbH 2018, abgerufen am 29. Dez. 2021

[11] 90° minus Schiefe der Ekliptik (23° 26' 21,412" gemäß Simon et al.: Numerical expressions…)

[AstrphQuant_S12-12] A. N. Cox (Hrsg.): Allen's Astrophysical Quantities. 4. Auflage. Springer Science+Business Media, New York 2004, ISBN 0-387-98746-0, S. 12.

[MeeusMoreMorselsKap33-14] J. Meeus: More Mathematical Astronomy Morsels. Willmann-Bell, Richmond 2002, ISBN 0-943396-74-3, Kap. 33

[Berger_Loutre_1994-15] A. Berger, M. F. Loutre: Precession, Eccentricity, Obliquity, Insolation and Paleoclimates. In: J.-C. Duplessy, M.-T. Spyridakis (Hrsg.): Long-Term Climatic Variations. NATO ASI Series, Band I 22 (1994) S. 107–152 (PDF, 5,1 MB). Der zeitliche Mittelwert von (a/r)² ist $\textstyle \left\langle {\frac {a^{2}}{r^{2}}}\right\rangle \,=\,{\frac {1}{T}}\int _{0}^{T}\left({\frac {a}{r}}\right)^{2}dt\,=\,{\frac {1}{\sqrt {1-\varepsilon ^{2}}}}$ .

[MeeusMorselsKap27-18] J. Meeus: Mathematical Astronomy Morsels. Willmann-Bell, Richmond 1997, ISBN 0-943396-51-4, Kap. 27

[19] Earth at Perihelion and Aphelion: 1501 to 1600 … Earth at Perihelion and Aphelion: 2001 to 2100 … Earth at Perihelion and Aphelion: 2401 to 2500 von Fred Espenak (astropixels.com), abgerufen 8. Juli 2021

[Bauer_2005-20] Eva Bauer: Klimafaktoren und Klimaänderungen im letzten Jahrtausend. In: Sterne und Weltraum. Dezember 2005, S. 31–38. PDF (932 kB) (Memento vom 4. März 2016 im Internet Archive)

[MeeusAstrAlgKap31-21] J. Meeus: Astronomical Algorithms. 2. Auflage. Willmann-Bell, Richmond 2000, ISBN 0-943396-61-1, Kap. 31

[Woerkom-22] A. J. J. van Woerkom: Note about galactic precession. In: Bulletin of the Astronomical Institutes of the Netherlands. Band 9, (1943), S. 427 (online)

[AstronomicalAlmanac_2012_SE2-23] R. S. Steadly, M. S. Robinson (Hrsg.): The Astronomical Almanac for the Year 2012. U.S. Government Printing Office, ISBN 978-0-7077-4121-5, S. E2.

[Owen-24] W. M. Owen, Jr.: A Theory of the Earth's Precession Relative to the Invariable Plane of the Solar System. Dissertation, University of Florida 1990, Abb. 5–1, S. 253 (online)

[SouamiSouchay_S11-25] D. Souami, J. Souchay: The solar system's invariable plane. In: Astronomy & Astrophysics. Band 543, Juli 2012, article nr. A133, doi:10.1051/0004-6361/201219011

[ExplSuppl_S99-26] P. K. Seidelmann (Hrsg.): Explanatory Supplement to the Astronomical Almanac. University Science Books, Mill Valley 1992, ISBN 0-935702-68-7, S. 99.

[ExplSuppl2013_S212-27] S. E. Urban, P. K. Seidelmann (Hrsg.): Explanatory Supplement to the Astronomical Almanac. 3. Auflage. University Science Books, Mill Valley 2013, ISBN 978-1-891389-85-6, S. 212.

[MeeusMoreMorselsKap27-28] J. Meeus: More Mathematical Astronomy Morsels. Willmann-Bell, Richmond 2002, ISBN 0-943396-74-3, Kap. 27

[Laskar2004_S268ff-29] J. Laskar, P. Robutel, F. Joutel, M. Gastineau, A.C.M. Correia, B. Levrard: A long-term numerical solution for the insolation quantities of the Earth. Astronomy & Astrophysics 428, 261–285 (2004), doi:10.1051/0004-6361:20041335, S. 268ff und Fig. 11

[HughesEmerson-30] D. W. Hughes, B. Emerson: The stability of the node of the Perseid meteor stream. In: The Observatory. Band 102, 1982, S. 39–42. (online)

[IMCCE2-32] IMCCE: Le manuel des éclipses. EDP Sciences, Les Ulis 2005, ISBN 2-86883-810-3, S. 85ff.

[AstronomicalAlmanac_2012_SC2-33] R. S. Steadly, M. S. Robinson (Hrsg.): The Astronomical Almanac for the Year 2012. U.S. Government Printing Office, ISBN 978-0-7077-4121-5, S. C2.

[Laskar2013_S19-34] J. Laskar: Is the Solar System stable? In: Progress in Mathematical Physics. 66, 2013, S. 239–270 (preprint, S. 19)

[Laskar1996_S147ff-35] J. Laskar: Large Scale Chaos and Marginal Stability in the Solar System. In: Celestial Mechanics and Dynamical Astronomy. Band 64, 1996, Heft 1–2, S. 115–162 (online), S. 147ff.

[Laskar2013_S27-36] J. Laskar: Is the Solar System stable? In: Progress in Mathematical Physics. 66, 2013, S. 239–270 (preprint, S. 27)

[Zeebe-37] R. E. Zeebe: Dynamic stability of the Solar System: Statistically inconclusive results from ensemble integrations. In: The Astrophysical Journal. accepted (arxiv:1506.07602 preprint)

[Laskar1996_S155-38] J. Laskar: Large Scale Chaos and Marginal Stability in the Solar System. In: Celestial Mechanics and Dynamical Astronomy. Band 64, 1996, Heft 1–2, S. 115–162 (online), S. 155.

[Montenbruck_S139-39] O. Montenbruck: Grundlagen der Ephemeridenrechnung. 6. Auflage. Verlag Sterne und Weltraum, Heidelberg 2001, ISBN 3-87973-941-2, S. 139.

[ExplSuppl2013_S338-41] S. E. Urban, P. K. Seidelmann (Hrsg.): Explanatory Supplement to the Astronomical Almanac. 3. Auflage. University Science Books, Mill Valley 2013, ISBN 978-1-891389-85-6, S. 338 (Kap. 8.10: Keplerian Elements for Approximate Positions of the Major Planets.) (preprint, PDF 68 kB)

[vanFlandern_Pulkkinen_1979-42] T. C. Van Flandern, K. F. Pulkkinen: Low-precision Formulae for Planetary Positions. In: Astrophysical Journal Supplement Series. Band 41 (Nov. 1979) S. 391–411 (online)

[JPL_FTP-43] Ephemeriden-Dateien auf dem FTP-Server des JPL: (siehe README.txt)

[JPL_HORIZONS-44] Ephemeriden-Server des JPL zum direkten Abruf von Planetenpositionen: ssd.jpl.nasa.gov

[IMCCE_INPOP-45] IMCCE: INPOP13c, a 4-D planetary ephemeris (abgerufen am 8. Januar 2015)

[Pitjeva_2013-46] E. V. Pitjeva: Updated IAA RAS Planetary Ephemerides-EPM2011 and Their Use in Scientific Research. In: Solar System Research. Band 47, Heft 5, September 2013, S. 386–402. (doi:10.1134/S0038094613040059, preprint)