Äquinoktium

Äquinoktium (Plural Äquinoktien, von lateinisch aequus ‚gleich‘ und nox ‚Nacht‘) oder Tagundnachtgleiche (auch Tag-und-Nacht-Gleiche) werden die beiden Kalendertage eines Jahres genannt, an denen lichter Tag und Nacht etwa gleich lang sind.

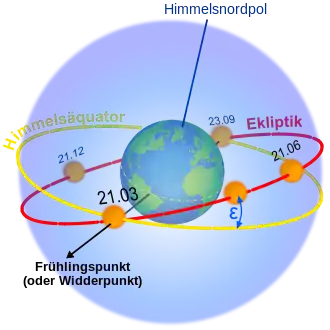
Die wahren Äquinoktien sind die Momente, in denen die Sonne bei ihrer scheinbaren Jahresbewegung auf der Ekliptik den Himmelsäquator überschreitet

Das gilt an jedem Ort (die unmittelbare Umgebung der Pole ausgenommen) auf der Erde. Die Sonne geht an diesen Tagen überall auf der Erde fast genau im Osten auf und im Westen unter. Die genauen Zeitpunkte der sogenannten wahren Äquinoktien sind die Momente, in denen die Sonne über den Himmelsäquator auf- (Frühlingsäquinoktium) bzw. absteigt (Herbstäquinoktium, siehe rechts stehende Abbildung) und die Deklination den Wert δ = 0° hat. Weil sich δ während der Länge eines Tages schon geringfügig ändert, sind Tag und Nacht auch an den Äquinoktien nicht exakt gleich lang.[1]

Dass es nur zwei Tage im Jahr mit dieser besonderen Eigenschaft gibt, liegt daran, dass die Erdachse ihre Bahnebene um die Sonne nicht senkrecht schneidet (siehe rechts stehende Abbildung), aber ihre Richtung im All beibehält und von der Sonne aus gesehen während des Erdumlaufs relativ zur Bahnebene taumelt.

Die Tagundnachtgleichen fallen auf den 19., 20. oder 21. März (Frühlingsäquinoktium),[2] und auf den 22., 23. oder 24. September (Herbstäquinoktium).[3] Sie markieren den kalendarischen Anfang der astronomisch definierten Jahreszeiten Frühling beziehungsweise Herbst. Im Jahr 2021 sind die Momente der wahren Äquinoktien 10:37 MEZ am 20. März und 21:21 MESZ am 22. September.[4]

Auch auf anderen Planeten gibt es Tagundnachtgleichen und folglich auch Jahreszeiten. Beim Saturn ist die Achsenneigung ε = 26,7°. Bei einer Umlaufzeit um die Sonne von rund 30 Erdenjahren tritt ein Äquinoktium dort nur etwa alle 15 Erdenjahre auf.

Die Tagundnachtgleichen wurden von vielen Völkern im Lauf der Menschheitsgeschichte gefeiert. Die Maya errichteten beispielsweise die Stufenpyramide El Castillo in Chichén Itzá in Mexiko. Die Architektur des Gebäudes ist so konzipiert, dass das Sonnenlicht an den Tagundnachtgleichen die Treppenstufen der Nordseite zu Mittag streift, während die Bereiche neben der Treppe im Schatten bleiben.[5]

Tatsächliche Erdbahn um die Sonne. Äquinoktien im März und im September, wenn die Erdachse der Sonne nicht zu- bzw. nicht weggeneigt ist.

Begriffsbestimmungen

Als Äquinoktium werden auf die Nordhalbkugel der Erde bezogen folgende Sachverhalte bezeichnet:

Zeitpunkte

Tagundnachtgleichen: Die Kalendertage, an denen die Sonne den Himmelsäquator überquert, und mit denen daher Frühling und Herbst anfangen.
- Primäräquinoktium: Querung von Süden her nach Norden, Frühlingsanfang.
- Sekundäräquinoktium: Querung von Norden nach Süden hin, Herbstanfang.
Wahre Äquinoktien: Die exakten Zeitpunkte, in denen die Sonne zu den Tagundnachtgleichen den Himmelsäquator quert, und damit der genaue Beginn der astronomischen Jahreszeiten Frühling oder Herbst.
- Frühlingsäquinoktium: Exakter Zeitpunkt des Frühlingsanfangs, am 19., 20. oder 21. März.
- Herbstäquinoktium: Exakter Zeitpunkt des Herbstanfangs, am 22., 23. oder 24. September.

Orte am Himmel

Äquinoktialpunkte: Die beiden Punkte auf der Ekliptik, an denen sich die Sonne bei wahrem Äquinoktium befindet:
- Frühlingspunkt
- Herbstpunkt
Mittlere Äquinoktialpunkte: Die beiden Punkte auf der Ekliptik, an denen sich die Sonne im langjährigen Mittel bei wahrem Äquinoktium befindet:
- Widderpunkt
- Waagepunkt

Tagundnachtgleichen als Jahresanfang und bestimmendes Datum für religiöse Feste

In einigen Kalendersystemen ist die Frühlingsgleiche der Jahresbeginn und eines der zentralen Feste des Jahres, so als Nouruz (wörtlich „Neulicht“) des astronomisch-solaren iranischen Kalenders und des Bahai-Kalenders. Rosch ha-Schana, der jüdische Neujahrstag, ist nicht identisch mit der Herbstgleiche, aber davon abhängig (eine begrenzte Zeit vorher bis eine begrenzte Zeit nachher). Analog verhält es sich mit dem jüdischen Pessachfest und dem christlichen Ostern, die immer innerhalb etwa eines Monats nach der Frühlingsgleiche stattfinden.

Äquinoktium als Jahreszeitenbeginn

Astronomischer Beginn des Frühlings und des Herbstes, wahres Äquinoktium

Äquinoktium (2015 bis 2028)
Jahr	Primär-		Sekundär-
Jahr	Tag	Uhrzeit MEZ	Tag	Uhrzeit MESZ
2015	20. Mrz.	23:45	23. Sep.	10:21
2016	20. Mrz.	05:30	22. Sep.	16:21
2017	20. Mrz.	11:29	22. Sep.	22:02
2018	20. Mrz.	17:15	23. Sep.	03:54
2019	20. Mrz.	22:58	23. Sep.	09:50
2020	20. Mrz.	04:50	22. Sep.	15:31
2021	20. Mrz.	10:37	22. Sep.	21:21
2022	20. Mrz.	16:33	23. Sep.	03:04
2023	20. Mrz.	22:24	23. Sep.	08:50
2024	20. Mrz.	04:06	22. Sep.	14:43
2025	20. Mrz.	10:01	22. Sep.	20:19
2026	20. Mrz.	15:45	23. Sep.	02:05
2027	20. Mrz.	21:24	23. Sep.	08:01
2028	20. Mrz.	03:16	22. Sep.	13:45

Die genaue Definition lautet:[6]

Die Äquinoktien sind die Zeitpunkte, zu denen die scheinbare geozentrische ekliptikale Länge der Sonne 0° respektive 180° beträgt.^*

* Scheinbar heißt: nach rechnerischer Eliminierung der durch Aberration und Nutation verursachten Verschiebungen.

* Geozentrisch heißt: von einem (hypothetischen) Beobachter im Erdmittelpunkt aus gesehen.

Die Definition ist also unabhängig vom Standort eines realen Beobachters; die Äquinoktien treten weltweit zum selben Zeitpunkt ein, der aber in verschiedenen Zeitzonen verschiedenen Uhrzeiten entspricht.

Diese Zeitpunkte fallen bis auf wenige Sekunden mit den Zeitpunkten zusammen, in denen der Mittelpunkt der Sonnenscheibe den Himmelsäquator durchquert, in denen die Sonne also von der südlichen zur nördlichen Himmelshälfte (ekliptikale Länge 0°) oder von der nördlichen zur südlichen Himmelshälfte (ekliptikale Länge 180°) überwechselt. Die Zeitdifferenz resultiert aus dem Umstand, dass es eigentlich der Schwerpunkt des Erde-Mond-Systems ist, der sich in der mittleren Erdbahnebene um die Sonne bewegt, während die Erde selbst diesen Schwerpunkt umkreist („wahre Erdbahn“) und sich somit – da die Bahnebene des Erde-Mond-Systems gegenüber der Erdbahnebene leicht geneigt ist – in der Regel etwas oberhalb oder unterhalb dieser Ebene befindet. Vom geozentrischen Beobachter aus gesehen läuft daher die Sonne nicht exakt auf der Ekliptik (und hat eine ekliptikale Breite ungleich Null). Sie passiert auch nicht exakt den Frühlings- bzw. Herbstpunkt und überquert den Äquator, bevor oder nachdem sie die ekliptikale Länge dieser Punkte erreicht hat. Dieser Zeitunterschied macht einige Sekunden aus.

Weil die durchschnittliche Dauer eines Umlaufs der Erde um die Sonne bezogen auf den Frühlingspunkt (tropisches Jahr) mit etwa 365,2422 Tagen knapp sechs Stunden länger ist als die Dauer des kalendarischen Gemeinjahres mit genau 365 Tagen, verschiebt sich das kalendarisch angegebene Datum der Äquinoktien von einem Gemeinjahr zum nächsten auf eine um etwa sechs Stunden spätere Uhrzeit. Mit der Einfügung des 29. Februars in einem Schaltjahr ergibt sich eine im Vergleich zum Vorjahr um etwa 18 Stunden frühere Uhrzeit für den Äquinoktialzeitpunkt. Die folgenden Angaben[7] der Äquinoktien sind auf Minuten gerundet (zum Beginn der vier Jahreszeiten siehe auch Tabelle im Artikel Jahreszeiten).

^* Bezogen auf die jeweils aktuelle Epoche.

Tagundnachtgleichen

Die Tagundnachtgleichen sind die verkürzt auf den Kalendertag angegebenen Zeitpunkte des astronomischen Beginns von Frühling beziehungsweise Herbst. Auf der Nordhalbkugel der Erde beginnt der Frühling im März und der Herbst im September. Auf der Südhalbkugel ist es jeweils umgekehrt.

Die Sonne überquert zur Tagundnachtgleiche den Himmelsäquator, steht also an diesem Tag um den Zeitpunkt des Äquinoktiums senkrecht über dem Erdäquator. Tag und Nacht sind dann überall auf der Erde ungefähr gleich lang, da eine Hälfte der täglichen Sonnenbahn oberhalb (Tagbogen), die andere unterhalb des Horizonts liegt. Überall auf der Erde geht die Sonne an diesem Tag daher fast genau im Osten auf und im Westen unter (siehe Aufgangspunkt).

In der sphärischen Astronomie werden Himmelsobjekte vereinfacht behandelt und die Ausdehnung der Sonnenscheibe bleibt zunächst unberücksichtigt, ebenso wie atmosphärische Einflüsse. Wegen der atmosphärischen Brechung des Sonnenlichts und der Bezugnahme auf den ersten bzw. letzten Sonnenstrahl haben allerdings tatsächlich zum Termin einer „Tagundnachtgleiche“ die Zeitspannen von lichtem Tag und Nacht nicht gleiche Dauer, sondern die Nacht ist um einige Minuten kürzer (siehe unten Equilux).

Zwischen den Äquinoktien liegen die Sonnenwenden, also die Tage, an denen die Sonne ihren größten Abstand vom Himmelsäquator erreicht und senkrecht über einem der Wendekreise der Erde steht. Die beiden Äquinoktien und die beiden Sonnenwenden in einem Jahr stellen jeweils den Beginn der astronomischen Jahreszeiten dar.

Equilux

Mit „Equilux“ wird ein Kalendertag bezeichnet, an dem auf der Erdoberfläche bei idealem (mathematischem) Horizont die Belichtungsdauer, gemessen zwischen dem ersten Sonnenstrahl morgens und dem letzten Sonnenstrahl abends, genau zwölf Stunden betragen würde; diese Definition bezieht sich also auf den Rand der Sonnenscheibe, nicht deren Mitte. Das Datum des Equilux fällt daher nicht auf das Datum eines Äquinoktiums („Equinox“), sondern findet im Jahreslauf einige Tage vor dem Primär- bzw. nach dem Sekundäräquinoktium statt. Im Gegensatz zu den erdmittelpunktbezogenen und so weltweit gleichen Äquinoktien hängt das Equilux-Datum darüber hinaus jeweils vom Breitengrad des Standortes ab. Für den 40. Breitengrad liegt es um den 17. März bzw. den 26. September, für den 5. Breitengrad um den 25. Februar bzw. den 15. Oktober.[8]

Die Sonne geht auf, wenn ihr oberer Rand über der Horizontlinie sichtbar wird, bevor also ihr Mittelpunkt erscheint. Der Sonnenuntergang ereignet sich, nachdem der Sonnenscheibenmittelpunkt scheinbar unter den Horizont gesunken ist, wenn der letzte Sonnenstrahl des oberen Sonnenrandes erlischt. Gegenüber einer punktförmigen Betrachtung der Sonnenmitte kommt damit je ein halber Durchmesserbogen der Sonne (etwa 0,27° bzw. 16′) hinzu. Außerdem bewirkt die Lichtbrechung durch die Erdatmosphäre jeweils eine scheinbare Anhebung der Sonnenscheibe (um etwa 0,6° bzw. 34′). Diese Verlängerung des lichten Tages auf Kosten der Nacht um knapp 7 Minuten (1,7 Winkelgrad × 4 Minuten/Winkelgrad) am Äquator (in Mitteleuropa um knapp 11 Minuten) wird bei der Bestimmung des Equilux berücksichtigt.

Äquinoktium als Koordinatennullpunkt

Wahres Äquinoktium und mittleres Äquinoktium

Die wahren Äquinoktialpunkte sind die tatsächlichen Schnittpunkte des Himmelsäquators mit der Ekliptik:

Der Durchgang der Sonne durch den Frühlingspunkt definiert den astronomischen Frühlingsanfang.
Der Durchgang der Sonne durch den Herbstpunkt definiert den astronomischen Herbstanfang.

Die mittleren Äquinoktialpunkte hingegen sind fiktiv. Sie sollen nur die langperiodische Bahnbewegung widerspiegeln, weswegen bei ihrer Bestimmung keine kurzfristigen Störungen (zum Beispiel Nutation und Aberration) berücksichtigt werden. Daher können die mittleren Äquinoktialpunkte von den tatsächlichen um mehrere Stunden abweichen.

Der mittlere Frühlingspunkt ist der „Widderpunkt“, benannt nach dem Sternbild Widder.
Der mittlere Herbstpunkt ist der „Waagepunkt“, benannt nach dem Sternbild Waage.

Das übliche Symbol für den Widderpunkt, der eine herausragende Bedeutung in der Himmelsmechanik hat, ist ${\mathcal {W}}$ oder ♈ (U+2648). Er ist der Koordinatennullpunkt für ekliptikale Koordinaten und äquatoriale Koordinaten und etliche andere astronomische Grundgrößen. Seine englische Bezeichnung ist first point of Aries.

Frühlingspunkt und Herbstpunkt

Auch der Frühlings- und der Herbstpunkt selbst, also jene Punkte, auf denen die Sonne zum Zeitpunkt eines Äquinoktiums im obigen Sinne vor dem Fixsternhintergrund steht, heißen Äquinoktien. In deutlicher unterscheidendem Sprachgebrauch werden sie auch als „Äquinoktialpunkte“ bezeichnet.

Der Frühlingspunkt ist der Punkt auf der imaginären Himmelskugel, bei dem die Sonne auf ihrer auf diese Kugel projizierten Bahn, der Ekliptik, auf dem Weg von Süden nach Norden den Himmelsäquator durchschneidet (Rektaszension = 0 h).

Dementsprechend ist der Herbstpunkt der Punkt auf der imaginären Himmelskugel, bei dem die Sonne auf ihrer auf diese Kugel projizierten Bahn den Himmelsäquator auf dem Weg von Norden nach Süden durchschneidet (Rektaszension = 12 h).

Im Winkel von 90° zum Frühjahrspunkt und Herbstpunkt liegen der Sommerpunkt (Rektaszension = 6 h) und der Winterpunkt (Rektaszension = 18 h), in denen die Sonne bei den Sonnenwenden steht.

Äquinoktiallinie

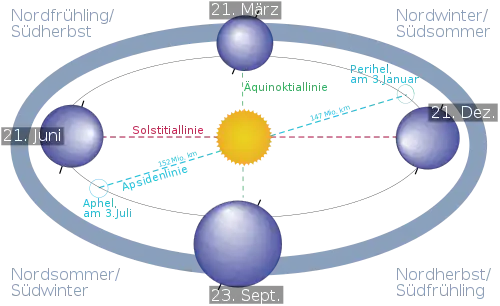
Die Verbindungslinie zwischen den beiden Positionen der Erde zum Zeitpunkt eines Äquinoktiums wird Äquinoktiallinie genannt. Diese Linie geht also mitten durch die Sonne hindurch, ihre Verlängerung außerhalb der Erdbahn durch die Äquinoktialpunkte. Sie steht senkrecht auf der Solstitiallinie.

Frühlingspunkt als Koordinatennullpunkt

Im Zusammenhang mit astronomischen Koordinatensystemen bezeichnet der Begriff „Äquinoktium“ stets den Frühlingspunkt, nie den Herbstpunkt. Der Frühlingspunkt dient sowohl für das äquatoriale wie für das ekliptikale Koordinatensystem als Nullpunkt, von dem aus Rektaszension bzw. ekliptikale Länge gezählt werden (nach Osten positiv). Der Frühlingspunkt ist zwar kein direkt beobachtbarer und anmessbarer Punkt, aber seine Lage kann stets aus geeigneten Beobachtungen rechnerisch ermittelt werden.

Wanderung der Äquinoktialpunkte

Die Gravitation von Sonne, Mond und Planeten verursacht Gezeitenkräfte. Durch diese entsteht ein Kräftepaar, das den Äquatorwulst der rotierenden Erde, deren Achse nicht 90°, sondern nur etwa 66,5° gegen die Ekliptikebene geneigt ist, in diese Ebene hinein zu drehen strebt – und damit dazu tendiert, die Rotationsachse bezüglich der Ekliptikebene weiter aufzurichten.

Die Erdachse richtet sich jedoch nicht auf. Vielmehr behält sie den Neigungswinkel bei und ändert ähnlich wie bei einem Kreisel langsam ihre Ausrichtung, sodass die Richtung, in die sie geneigt ist, während etwa 25.800 Jahren einmal volle 360° durchläuft. Auch die senkrecht zur Erdachse definierte Äquatorebene vollzieht diese Bewegung, sodass die Äquinoktialpunkte als die Schnittpunkte von Äquatorebene und Ekliptikebene in 25.800 Jahren einmal rund um die Ekliptik durchlaufen. Diese Bewegung der Erdachse beziehungsweise der Äquinoktialpunkte bezeichnet man als Präzession (lateinisch für „Vorangehen“).

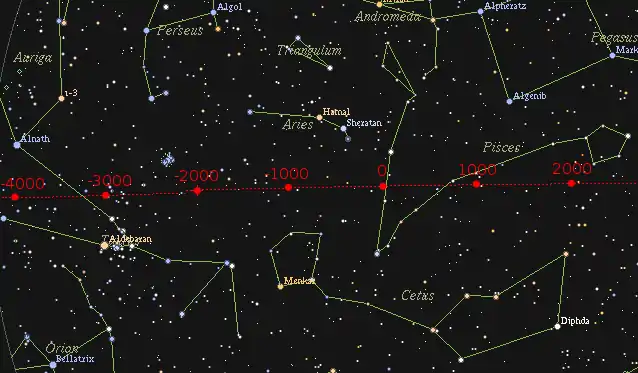
Der Frühlingspunkt wandert längs der Ekliptik in sechs Jahrtausenden um fast ein Viertel der Himmelskugel

Die Äquinoktialpunkte verschieben sich dabei pro Jahr um etwa 50 Bogensekunden in westlicher Richtung entlang der Ekliptik. Dieser Effekt ist so groß, dass er über einen Beobachtungszeitraum von einigen Jahrzehnten auffällt, und war schon in der Antike bekannt.

Der Präzessionsbewegung überlagern sich noch zusätzliche periodische Schwankungen. Sie liegen an der Schiefe der Umlaufbahn des Mondes, die um 5° 9′ gegen die Ekliptik geneigt ist, und an der sich kontinuierlich verschiebenden Knotenlinie der Mondumlaufbahn sowie an leichten periodischen Verlagerungen der Rotationsachse der Erde. Diese verschiedenen periodischen Bewegungen, welche die Erdachse zusätzlich zur Präzession ausführt, werden in der Astronomie zusammengefasst unter dem Begriff der Nutation. Die Verschiebung der Äquinoktialpunkte entlang der Ekliptik erfolgt also nicht völlig gleichmäßig, sondern mit periodisch leicht schwankender Geschwindigkeit.

Die Straßburger Münsteruhr enthält eine Vorrichtung, mit der auch die Präzession dargestellt wird (nicht aber die Nutation).

Das Äquinoktium von astronomischen Koordinaten

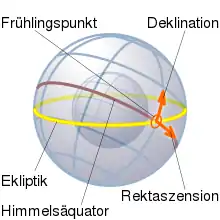
Ekliptikales und äquatoriales Koordinatensystem haben die Äquinoktien als gemeinsamen Fixpunkt

Die Wanderung der Äquinoktialpunkte hat insbesondere zur Folge, dass die Nullpunkte der oben genannten astronomischen Koordinatensysteme nicht im Raum fixiert sind, sondern mit dem Frühlingspunkt langsam entlang der Ekliptik wandern. So nimmt zum Beispiel die ekliptikale Länge eines Sterns ohne Eigenbewegung in einem Jahr um 50 Bogensekunden zu, d. h. in 100 Jahren um 1,4°. Die Koordinaten eines Himmelsobjekts ändern sich also, ohne dass dies einer eigentlichen Bewegung des Objekts entspricht. Bei ihrer Angabe muss deshalb stets der Zeitpunkt, also die Lage des Frühlingspunkts, angegeben werden, auf den sich die Koordinaten beziehen. Dieser Zeitpunkt (nicht zu verwechseln mit einer der Tagundnachtgleichen) heißt ebenfalls Äquinoktium und wird als Jahreszahl, gegebenenfalls mit Bruchteil, angegeben. Von Bedeutung für Beobachtungen sind die Koordinaten für das Äquinoktium des Beobachtungszeitpunkts (zum Beispiel 2005,432), das sogenannte Äquinoktium des Datums.

Die Umrechnung von Koordinaten zwischen verschiedenen Äquinoktien ist eine häufig anzutreffende Aufgabe.

Äquinoktium und Epoche

Nicht mit dem Äquinoktium verwechselt werden darf der Begriff der Epoche. Die Epoche bezeichnet den tatsächlichen Zeitpunkt einer Beobachtung oder eines Vorgangs: das Äquinoktium des Koordinatensystems, in dem gemessen wird.

Standardäquinoktien

Kataloge von Himmelsobjekten werden in der Regel auf sogenannte Standardäquinoktien bezogen. Das sind Koordinatensysteme, die auf bestimmte Zeitpunkte bezogen sind und auch Standardepochen genannt werden. Die Zeitpunkte sind zum Wechsel jedes 25. Jahres festgelegt. Früher betrug der Zeitunterschied zwischen zwei Standardepochen 25 besselsche Jahre (ca. 9131,055 Tage), heute sind es 25 julianische Jahre (9131,25 Tage). Diese Standardäquinoktien werden mit einer Jahreszahl und einem B oder J davor bezeichnet, das sind:

Standardepoche/ -Äquinoktium	Datum		Anmerkung
Standardepoche/ -Äquinoktium	Julianisch	Gregorianisch	Anmerkung
B1850	2396758,203	31. Dez. 1849, 16:52 UT	Heutzutage bedeutungslos
B1875	2405889,258	31. Dez. 1874, 18:12 UT	Nach dem Äquinoktium dieser Epoche wurden die exakten Sternbildgrenzen als Linien konstanter Rektaszension oder konstanter Deklination festgelegt.
B1900	2415020,313	31. Dez. 1899, 19:31 UT
B1925	2424151,368	31. Dez. 1924, 20:50 UT	Heutzutage bedeutungslos
B1950	2433282,423	31. Dez. 1949, 22:09 UT	Die Sternpositionen im vierten Fundamentalkatalog sind mit diesem Äquinoktium angegeben.
B1975	2442413,478	31. Dez. 1974, 23:28 UT	Letztes Standardäquinoktium, das sich auf eine besselsche Epoche bezieht (sehr selten verwendet).
J2000	2451545,000	01. Jan. 2000, 12:00 UT	Wurde unabhängig von den vorherigen Zeitpunkten exakt so festgelegt, um glatte Zeitpunkte zu erhalten. Dieses Äquinoktium ist heute in Verwendung.

Beispiel: Der Stern Arktur hat zu verschiedenen Epochen die folgenden auf verschiedene Äquinoktien bezogenen äquatorialen Koordinaten Rektaszension und Deklination:

Epoche	Äquinoktium
Epoche	J2000.0	des Datums	J2050.0
01. Jan. 2000	213,9153° / 19,1824°	213,9153° / 19,1824°	214,5019° / 18,9522°
12. Aug. 2028	213,9061° / 19,1665°	214.2418° / 19,0346°	214,4928° / 18,9363°
01. Jan. 2050	213,8992° / 19,1546°	214,4860° / 18,9244°	214,4860° / 18,9244°

Die Änderung der Koordinaten für verschiedene Epochen, aber dasselbe fixe Äquinoktium (J2000.0 oder J2050.0) spiegelt die Eigenbewegung des Sterns wider. Die Verschiedenheit der Koordinaten für dieselbe Epoche, aber unterschiedliche Äquinoktien ist auf die Präzession zurückzuführen. Die im Äquinoktium des Datums gegebenen Koordinaten beinhalten den Einfluss sowohl der Eigenbewegung als auch der Präzession.

Für Berechnungen ist es oft vorteilhaft, den periodischen Einfluss der Nutation auf die Bewegung des Äquinoktiums zu ignorieren und sich auf ein fiktives gleichmäßig bewegtes Äquinoktium zu beziehen (die Nutation muss dann natürlich nachträglich auf die Resultate wieder addiert werden). Es handelt sich dann um das mittlere Äquinoktium, während das wahre Äquinoktium den Einfluss der Nutation enthält.

Katalogäquinoktium und dynamisches Äquinoktium

Die genaue Lage des Äquinoktiums muss ebenso wie die Lage des Äquators und der Ekliptik durch Beobachtung bestimmt werden. Dazu wird gelegentlich geeignetes Beobachtungsmaterial besonders sorgfältig ausgewertet. Das Ergebnis ist zum Beispiel ein Sternkatalog, dessen Koordinatenangaben möglichst genau die Position der Sterne bezüglich des gesuchten Äquinoktiums angeben. Diese Koordinaten verkörpern das Koordinatensystem für den praktischen Gebrauch und stellen ein Fundamentalsystem dar, auf das sich andere Positionsmessungen beziehen können. Werden zum Beispiel die Koordinaten eines Sterns bestimmt, indem sein Abstand von geeigneten Fundamentalsternen gemessen wird, so beziehen sich seine gefundenen Koordinaten automatisch auf das Äquinoktium des Fundamentalsystems. Das Äquinoktium, das aus Katalogpositionen abgeleitet wird (als Schnittpunkt des Stundenkreises der Rektaszension 0 mit dem Äquator), ist das Katalogäquinoktium. Das vom Fundamentalsystem verkörperte Äquinoktium fällt aufgrund unvermeidlicher Messungenauigkeiten nie völlig exakt mit dem tatsächlichen Äquinoktium zusammen. Bei hohen Genauigkeitsansprüchen ist daher der Katalog anzugeben, auf dessen Katalogäquinoktium sich die Messungen beziehen. Wird das Äquinoktium ausschließlich aus Planetenbeobachtungen abgeleitet (der Drehimpulsvektor der Erdbewegung steht beispielsweise senkrecht auf der Ekliptikebene und erlaubt, diese zu bestimmen), so erhält man ein dynamisches Äquinoktium.

Umrechnung von einem Äquinoktium in ein anderes

Die folgenden Umrechnungen transformieren äquatoriale Koordinaten von einem Äquinoktium in ein anderes. Die Eigenbewegung astronomischer Objekte ist nicht berücksichtigt. Vorgehensweise:

Umrechnen der äquatorialen Koordinaten des bisherigen Äquinoktiums in kartesische Koordinaten (einer Einheitskugel).
Transformation der kartesischen Koordinaten in kartesische Koordinaten des Zieläquinoktiums mit Hilfe einer Drehmatrix.
Umrechnung der transformierten kartesischen Koordinaten in äquatoriale Koordinaten.

Umrechnung von äquatorialen Koordinaten in kartesische Koordinaten

Mit Rektaszension α und Deklination δ gilt für $P={\begin{pmatrix}x\\y\\z\end{pmatrix}}:$

$x=\cos(\alpha )\,\cos(\delta )$
$y=\sin(\alpha )\,\cos(\delta )$
$z=\sin(\delta )$

P={\begin{pmatrix}\cos(\alpha )\,\cos(\delta )\\\sin(\alpha )\,\cos(\delta )\\\sin(\delta )\end{pmatrix}}

Drehungen mit Hilfe einer Drehmatrix

P\cdot M=P'

{\begin{pmatrix}x\\y\\z\end{pmatrix}}\cdot {\begin{pmatrix}m_{11}&m_{12}&m_{13}\\m_{21}&m_{22}&m_{23}\\m_{31}&m_{32}&m_{33}\end{pmatrix}}={\begin{pmatrix}x'\\y'\\z'\end{pmatrix}}

Die Drehmatrix ergibt sich aus der Überlagerung von drei Drehungen um die mit Polynomen ermittelten Winkel $\zeta ,z$ und $\Theta$ :[6]

{\begin{pmatrix}\cos(\zeta )\cdot \cos(\Theta )\cdot \cos(z)-\sin(\zeta )\cdot \sin(z)&-\sin(\zeta )\cdot \cos(\Theta )\cdot \cos(z)-\cos(\zeta )\cdot \sin(z)&-\sin(\Theta )\cdot \cos(z)\\\cos(\zeta )\cdot \cos(\Theta )\cdot \sin(z)+\sin(\zeta )\cdot \cos(z)&-\sin(\zeta )\cdot \cos(\Theta )\cdot \sin(z)+\cos(\zeta )\cdot \cos(z)&-\sin(\Theta )\cdot \sin(z)\\\cos(\zeta )\cdot \sin(\Theta )&-\sin(\zeta )\cdot \sin(\Theta )&\cos(\Theta )\end{pmatrix}}

Das bedeutet für die Matrixmultiplikation:

x'=x\cdot m_{11}+y\cdot m_{12}+z\cdot m_{13}

y'=x\cdot m_{21}+y\cdot m_{22}+z\cdot m_{23}

z'=x\cdot m_{31}+y\cdot m_{32}+z\cdot m_{33}

Errechnen der äquatorialen Koordinaten des Zieläquinoktiums

\alpha '=\operatorname {sgn}(y')\cdot \arccos {\frac {x'}{\sqrt {x'^{2}+y'^{2}}}}

\delta '=\arcsin(z')

Umrechnungen zwischen Standardäquinoktien

Für die Standardäquinoktien B1875, B1900, B1950, B1975 und J2000 gelten folgende Matrizen:

Matrix B1875 → B1900 ${\begin{pmatrix}+0{,}999981452&-0{,}005585025&-0{,}002429486\\+0{,}005585008&+0{,}999984404&-0{,}000006789\\+0{,}002429496&-0{,}000006981&+0{,}999997049\end{pmatrix}}$	Matrix B1875 → B1950 ${\begin{pmatrix}+0{,}999833020&-0{,}016757867&-0{,}007288174\\+0{,}016757422&+0{,}999859575&-0{,}000061084\\+0{,}007288430&-0{,}000061087&+0{,}999973439\end{pmatrix}}$
Matrix B1875 → B1975 ${\begin{pmatrix}+0{,}999703104&-0{,}022343591&-0{,}009717233\\+0{,}022344281&+0{,}999750345&-0{,}000108598\\+0{,}009717840&-0{,}000108210&+0{,}999952781\end{pmatrix}}$	Matrix B1875 → J2000 ${\begin{pmatrix}+0{,}999535925&-0{,}027933851&-0{,}012144267\\+0{,}027935279&+0{,}999609760&-0{,}000169365\\+0{,}012147193&-0{,}000169297&+0{,}999926241\end{pmatrix}}$
Matrix B1900 → B1875 ${\begin{pmatrix}+0{,}999981452&+0{,}005585025&+0{,}002429486\\-0{,}005585008&+0{,}999984404&-0{,}000006784\\-0{,}002429496&-0{,}000006981&+0{,}999997049\end{pmatrix}}$	Matrix B1900 → B1950 ${\begin{pmatrix}+0{,}999925772&-0{,}011173365&-0{,}004858902\\+0{,}011173233&+0{,}999937576&-0{,}000027154\\+0{,}004858978&-0{,}000027925&+0{,}999988195\end{pmatrix}}$
Matrix B1900 → B1975 ${\begin{pmatrix}+0{,}999832961&-0{,}016761357&-0{,}007288174\\+0{,}016760912&+0{,}999859517&-0{,}000061097\\+0{,}007288430&-0{,}000061087&+0{,}999973439\end{pmatrix}}$	Matrix B1900 → J2000 ${\begin{pmatrix}+0{,}999702892&-0{,}022350570&-0{,}009717237\\+0{,}022353004&+0{,}999750189&-0{,}000108276\\+0{,}009719586&-0{,}000108210&+0{,}999952781\end{pmatrix}}$
Matrix B1950 → B1875 ${\begin{pmatrix}+0{,}999833020&+0{,}016757867&+0{,}007288175\\-0{,}016757422&+0{,}999859575&-0{,}000061059\\-0{,}007288430&-0{,}000061087&+0{,}999973439\end{pmatrix}}$	Matrix B1950 → B1900 ${\begin{pmatrix}+0{,}999925772&+0{,}011173365&+0{,}004858902\\-0{,}011173233&+0{,}999937576&-0{,}000027138\\-0{,}004858978&-0{,}000027925&+0{,}999988195\end{pmatrix}}$
Matrix B1950 → B1975 ${\begin{pmatrix}+0{,}999981433&-0{,}005588515&-0{,}002429486\\+0{,}005588499&+0{,}999984384&-0{,}000006797\\+0{,}002429496&-0{,}000006981&+0{,}999997049\end{pmatrix}}$	Matrix B1950 → J2000 ${\begin{pmatrix}+0{,}999925666&-0{,}011178601&-0{,}004858904\\+0{,}011181959&+0{,}999937517&-0{,}000026798\\+0{,}004860723&-0{,}000027925&+0{,}999988195\end{pmatrix}}$
Matrix B1975 → B1875 ${\begin{pmatrix}+0{,}999703104&+0{,}022343591&+0{,}009717234\\-0{,}022344281&+0{,}999750345&-0{,}000108547\\-0{,}009717840&-0{,}000108210&+0{,}999952781\end{pmatrix}}$	Matrix B1975 → B1900 ${\begin{pmatrix}+0{,}999832961&+0{,}016759612&+0{,}007288175\\-0{,}016760912&+0{,}999859546&-0{,}000061059\\-0{,}007288430&-0{,}000061087&+0{,}999973439\end{pmatrix}}$
Matrix B1975 → B1950 ${\begin{pmatrix}+0{,}999981433&+0{,}005586770&+0{,}002429486\\-0{,}005588499&+0{,}999984394&-0{,}000006780\\-0{,}002429496&-0{,}000006981&+0{,}999997049\end{pmatrix}}$	Matrix B1975 → J2000 ${\begin{pmatrix}+0{,}999981399&-0{,}005592006&-0{,}002429487\\+0{,}005593735&+0{,}999984365&-0{,}000006411\\+0{,}002431241&-0{,}000006981&+0{,}999997049\end{pmatrix}}$
MatrixJ2000 → B1875 ${\begin{pmatrix}+0{,}999535925&+0{,}027933851&+0{,}012146003\\-0{,}027935279&+0{,}999609760&-0{,}000170004\\-0{,}012147193&-0{,}000169297&+0{,}999926220\end{pmatrix}}$	Matrix J2000 → B1900 ${\begin{pmatrix}+0{,}999702948&+0{,}022350570&+0{,}009717230\\-0{,}022351260&+0{,}999750189&-0{,}000108954\\-0{,}009717840&-0{,}000108210&+0{,}999952781\end{pmatrix}}$
Matrix J2000 → B1950 ${\begin{pmatrix}+0{,}999925685&+0{,}011178601&+0{,}004858900\\-0{,}011180214&+0{,}999937517&-0{,}000027528\\-0{,}004860723&-0{,}000026180&+0{,}999988195\end{pmatrix}}$	Matrix J2000 → B1975 ${\begin{pmatrix}+0{,}999981399&+0{,}005592006&+0{,}002429485\\-0{,}005593735&+0{,}999984365&-0{,}000007162\\-0{,}002431241&-0{,}000006981&+0{,}999997049\end{pmatrix}}$

Beispiel

Für die Umrechnung von B1950 nach J2000 gelten die Werte $\zeta =1152{,}4075''$ , $z=1152{,}750''$ und $\Theta =1002{,}2442''$ , woraus sich die Matrix

{\begin{pmatrix}+0{,}9999257352&-0{,}0111761178&-0{,}0048598834\\+0{,}0111761178&+0{,}9999375449&-0{,}0000271607\\+0{,}0048598834&-0{,}0000271560&+0{,}9999881903\end{pmatrix}}

ergibt. Das bedeutet für die Matrixmultiplikation:

x'=x\cdot m_{11}+y\cdot m_{12}+z\cdot m_{13}=0{,}9999257352x-0{,}0111761178y-0{,}0048598834z

y'=x\cdot m_{21}+y\cdot m_{22}+z\cdot m_{23}=0{,}0111761178x+0{,}9999375449y-0{,}0000271607z

z'=x\cdot m_{31}+y\cdot m_{32}+z\cdot m_{33}=0{,}0048598834x-0{,}0000271560y+0{,}9999881903z

Für beispielsweise den Himmelspol des Äquinoktiums B1950 gilt:

\alpha =0^{\circ }

(beliebig wählbar)

\delta =+90^{\circ }

x=\cos(\alpha )\cdot \cos(\delta )=0

y=\sin(\alpha )\cdot \cos(\delta )=0

z=\sin(\delta )=1

{\begin{pmatrix}0\\0\\1\end{pmatrix}}\cdot {\begin{pmatrix}+0{,}9999257352&-0{,}0111761178&-0{,}0048598834\\+0{,}0111761178&+0{,}9999375449&-0{,}0000271607\\+0{,}0048598834&-0{,}0000271560&+0{,}9999881903\end{pmatrix}}={\begin{pmatrix}-0{,}0048619076\\-0{,}0000271833\\+0{,}9999881805\end{pmatrix}}

und daraus

\alpha '=180{,}320341641^{\circ }

\delta '\,=\;\;89{,}721427765^{\circ }

Literatur

Andreas Guthmann: Einführung in die Himmelsmechanik und Ephemeridenrechnung. 2. Auflage, Spectrum, Heidelberg 2000, ISBN 3-8274-0574-2.
Oliver Montenbruck: Grundlagen Der Ephemeridenrechnung. 7. Auflage, Spectrum, Heidelberg 2009, ISBN 978-3-8274-2291-0.
Manfred Schneider: Himmelsmechanik. 2. Auflage, Bibliographisches Institut, Mannheim/Wien/Zürich 1981, ISBN 3-411-01619-1.

Weblinks

Commons: Äquinoktium – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Äquinoktium – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Berechnung des Äquinoktiums von −4000 bis 2500. Institut de Mecanique Celeste et de Calcul des Ephemerides (IMCCE)
Wiebke Salzmann: Wissenstexte Physik-Wissen – Tageslänge und Jahreszeiten.

Einzelnachweise

Es gibt lediglich Orte mit genau gleichzeitigem Moment des Sonnenaufgangs und andere Orte mit genau gleichzeitigem Moment des Sonnenuntergangs. Sie liegen auf jeweils demselben Längengrad. Es handelt sich um ein und denselben Moment, nämlich den Zeitpunkt des (astronomischen) Äquinoktiums. Auf- und Untergangsmomente betreffen die Sonnenmitte im mathematischen Horizont, und die Lichtablenkung in der Erdatmosphäre ist vernachlässigt.
Christoph Neumüller: Frühlingsanfang von 1900 bis 2100. Bei: dasinternet.net. Abgerufen am 7. Januar 2021.
Christoph Neumüller: Herbstanfang von 1900 bis 2100. Bei: dasinternet.net. Abgerufen am 7. Januar 2021.
DATES DES SAISONS POUR UNE ANNEE DONNEE. In: promenade.imcce.fr. Institut de Mecanique Celeste et de Calcul des Ephemerides (IMCCE), abgerufen am 7. Januar 2021.
Rachel A. Becker: Das Äquinoktium ist da! Aber was ist das eigentlich? Bei: NationalGeographic.de. Abgerufen am 7. Januar 2021.
Jean Meeus: Astronomical Algorithms. Willmann-Bell, Richmond 2000, ISBN 0-943396-61-1.
Jahreszeitentabelle des USNO. (Memento vom 8. Oktober 2015 im Internet Archive). Bei: usno.navy.mil. Abgerufen am 7. Januar 2021.
Equinoxes. (Memento vom 25. September 2015 im Internet Archive). Bei: usno.navy.mil. Abgerufen am 7. Januar 2021.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Es gibt lediglich Orte mit genau gleichzeitigem Moment des Sonnenaufgangs und andere Orte mit genau gleichzeitigem Moment des Sonnenuntergangs. Sie liegen auf jeweils demselben Längengrad. Es handelt sich um ein und denselben Moment, nämlich den Zeitpunkt des (astronomischen) Äquinoktiums. Auf- und Untergangsmomente betreffen die Sonnenmitte im mathematischen Horizont, und die Lichtablenkung in der Erdatmosphäre ist vernachlässigt.

[2] Christoph Neumüller: Frühlingsanfang von 1900 bis 2100. Bei: dasinternet.net. Abgerufen am 7. Januar 2021.

[3] Christoph Neumüller: Herbstanfang von 1900 bis 2100. Bei: dasinternet.net. Abgerufen am 7. Januar 2021.

[4] DATES DES SAISONS POUR UNE ANNEE DONNEE. In: promenade.imcce.fr. Institut de Mecanique Celeste et de Calcul des Ephemerides (IMCCE), abgerufen am 7. Januar 2021.

[5] Rachel A. Becker: Das Äquinoktium ist da! Aber was ist das eigentlich? Bei: NationalGeographic.de. Abgerufen am 7. Januar 2021.

[Meeus-6] Jean Meeus: Astronomical Algorithms. Willmann-Bell, Richmond 2000, ISBN 0-943396-61-1.

[7] Jahreszeitentabelle des USNO. (Memento vom 8. Oktober 2015 im Internet Archive). Bei: usno.navy.mil. Abgerufen am 7. Januar 2021.

[8] Equinoxes. (Memento vom 25. September 2015 im Internet Archive). Bei: usno.navy.mil. Abgerufen am 7. Januar 2021.