Tropisches Jahr

Ein tropisches Jahr (von altgriechisch τρόπος (tropos) = Drehung, Wendung) ist, vereinfacht gesprochen, die Zeit zwischen zwei gleichen Zeitpunkten im Ablauf der Jahreszeiten, zum Beispiel von einer Frühlings-Tagundnachtgleiche (Frühlingsanfang) zur nächsten oder von einer Sommersonnenwende (Sommeranfang) zur nächsten. Von der Beziehung zur Sonnenwende leitet sich die Bezeichnung „tropisch“ ab.

Nun ist aber einerseits die Winkelgeschwindigkeit, mit der sich die Richtung der Verbindungslinie von der Erde zur Sonne ändert, entsprechend dem zweiten Keplerschen Gesetz periodisch veränderlich. Deshalb ersetzt man die Richtung der wahren Sonne durch die Richtung der mittleren Sonne, deren Winkelgeschwindigkeit keine periodischen Schwankungen aufweist. Andererseits bewegt sich auch die Bezugsrichtung, nämlich der Frühlingspunkt, auf die die Richtungsangabe der Sonne in der Ekliptik bezogen wird. Diese Bewegung setzt sich zusammen aus einem gleichmäßigen Anteil, der Präzession, mit einer Winkelgeschwindigkeit von rund 50″ pro Jahr und einem periodischen Anteil, der Nutation. Die nur mit der Präzession veränderliche mittlere Richtung des Frühlingspunkts ist der mittlere Frühlingspunkt. Die darauf bezogene Richtungsangabe der mittleren Sonne ist die mittlere ekliptikale Länge der Sonne. Ein tropisches Jahr ist nach genauer Definition der Zeitraum, in dem die mittlere ekliptikale Länge der Sonne um 360° zunimmt.

Wegen der Präzessionsbewegung des mittleren Frühlingspunktes ist ein tropisches Jahr rund 20 Minuten kürzer als ein siderisches Jahr, das gleich der Dauer eines Umlaufs der mittleren Sonne relativ zum ruhenden Sternhintergrund ist. Da für die Jahreszeiten nicht die Richtung der Sonne relativ zu den anderen Sternen, sondern relativ zum Frühlingspunkt maßgeblich ist, soll die Länge eines Kalenderjahres (das stets eine ganze Anzahl von Tagen enthält) im Mittel das tropische Jahr approximieren.

Die Länge des tropischen Jahres betrug zu Beginn des Jahres 2000 (Epoche J2000.0)

365,242.190.52 Tage = 365 Tage 5 Stunden 48 Minuten 45,261 Sekunden oder 31.556.925,261 Sekunden

Da die Präzessionsbewegung des mittleren Frühlingspunktes nicht mit konstanter Winkelgeschwindigkeit, sondern leicht beschleunigt erfolgt, ist die Länge des tropischen Jahres geringfügig veränderlich. Sie nimmt gegenwärtig um etwa eine halbe Sekunde pro Jahrhundert ab.

Einführung

Es gibt zwei unterschiedliche Definitionen des tropischen Jahres:

Die ältere versteht unter dem tropischen Jahr den Zeitraum zwischen zwei Durchgängen der Sonne durch den Frühlingspunkt. Diese Definition ist anschaulicher und unmittelbar der Beobachtung zugänglich. Es ist jedoch schwierig, ihr einen eindeutigen, allgemeingültigen Zahlenwert beizulegen. Der Zeitraum zwischen zwei solchen Durchgängen schwankt wegen der Gravitationseinflüsse der Planeten und des Mondes von Jahr zu Jahr um einige Minuten, so dass zur Bestimmung eines Referenzwertes über hinreichend viele Jahre gemittelt werden müsste. Da die Jahreslänge aber auch einer langfristigen Drift unterliegt, hängt das Ergebnis von der willkürlichen Wahl des Mittelungszeitraums ab. Zur rechnerischen Ermittlung dieser Jahreslänge kann von den mittleren Bahnelementen der Erde ausgegangen werden, aus welchen die genannten Störungen rechnerisch entfernt wurden. Am tropischen Jahr gemäß dieser älteren Definition orientiert sich die Jahreslänge der Sonnenkalender.
Die neuere Definition bezieht sich auf die momentane Geschwindigkeit, mit der sich die mittlere ekliptikale Länge der Sonne in Bezug auf den mittleren Frühlingspunkt ändert. Diese Geschwindigkeit ist nicht unmittelbar beobachtbar, sondern ergibt sich als mathematische Größe in den Planetentheorien. Die Definition ist also sehr abstrakt, ihr Zahlenwert ist jedoch wohldefiniert und präzise bestimmbar.

Je nach Definition ergeben sich leicht unterschiedliche Zahlenwerte. Die Länge des tropischen Jahres beträgt nach der alten Definition gegenwärtig ca. 365,2424 Tage (langsam zunehmend) und nach der neuen Definition gegenwärtig ca. 365,2422 Tage (langsam abnehmend). Auch in der Fachliteratur besteht häufig Verwirrung bezüglich der beiden Definitionen; oft wird die alte Definition angegeben, für die Jahreslänge jedoch der Zahlenwert nach der neuen Definition genannt.

Alte Definition: Rückkehr zum Frühlingspunkt

Grundlagen

In einem Sonnenkalender ist ein Jahr traditionell der Zeitraum, nach welchem sich die Jahreszeiten wiederholen, nach welchem also die Sonne auf ihrer scheinbaren jährlichen Bahn rund um den Fixsternhimmel wieder zum selben Punkt zurückkehrt.

Nachdem Hipparch die Präzession der Erde entdeckt hatte, war es notwendig geworden zu unterscheiden, ob „derselbe Punkt“ sich auf den Fixsternhintergrund oder auf die Äquinoktial- und Solstitialpunkte der Ekliptik (Tagundnachtgleichen bzw. Sonnenwenden) beziehen sollte. Der Zeitraum, den die Sonne zur Rückkehr zum selben (unendlich weit entfernt gedachten) Fixstern braucht, ist das siderische Jahr mit einer Länge von 365^d 6^h 9^m 10^s. Die Äquinoktial- und Solstitialpunkte hingegen wandern infolge der Präzession entlang der Ekliptik, und zwar der scheinbaren jährlichen Bewegung der Sonne entgegengerichtet (retrograd). Da diese Referenzpunkte ihr entgegenwandern, braucht die Sonne etwa 20 Minuten weniger, um z. B. wieder zum Frühlingspunkt zurückzukehren, gegenwärtig also etwa 365^d 5^h 48^m 45^s. Diesen Zeitraum der Wiederkehr zum Frühlingspunkt bezeichnete man als das tropische Jahr (von griechisch trope „Umkehr“, „Sonnwende“, weil ursprünglich auf die Sonnwendpunkte statt auf den Frühlingspunkt bezogen).

Da die Jahreszeiten von der Stellung der Sonne bezüglich der Äquinoktial- und Solstitialpunkte abhängen (so beginnt z. B. der astronomische Frühling, wenn die Sonne den Frühlingspunkt durchschreitet), ist das tropische Jahr und nicht das siderische Jahr maßgebend für den jährlichen Lebensrhythmus.

Bahnstörungen

Frühlingspunkt bis Frühlingspunkt
2000 → 2001	365^d 5^h 55^m 28^s
2001 → 2002	365^d 5^h 45^m 26^s
2002 → 2003	365^d 5^h 43^m 37^s
2003 → 2004	365^d 5^h 48^m 52^s
2004 → 2005	365^d 5^h 44^m 47^s
2005 → 2006	365^d 5^h 52^m 10^s
2006 → 2007	365^d 5^h 41^m 51^s

Die antiken und mittelalterlichen Astronomen hatten keinen Grund zu bezweifeln, dass die Länge des so definierten tropischen Jahres stets konstant sei. Zur Messung genügte es also, z. B. den Zeitabstand zwischen zwei beliebigen Frühlingsäquinoktien zu messen und durch die Anzahl der verflossenen Jahre zu dividieren. Die Newtonsche Gravitationstheorie zeigte jedoch, dass die Planeten ihre Bahnen gegenseitig geringfügig beeinflussen. Aufgrund dieser Bahnstörungen durchläuft die Erde ihre Bahn nicht immer in exakt dem gleichen Zeitraum. Die Tabelle gibt einige Beispiele für den zeitlichen Abstand zweier Durchgänge der Sonne durch den Frühlingspunkt.

Es wäre also notwendig gewesen, diese Störungen herauszurechnen oder einen Mittelwert über hinreichend viele tropische Jahre zu bilden, um einen eindeutigen Zahlenwert für die Länge des tropischen Jahres zu erhalten.

Elliptische Erdbahn

Neben diesen Bahnstörungen gibt es noch eine zweite Komplikation, die den Zeitraum zwischen zwei Frühlingsanfängen beeinflusst. Die Erde durchläuft ihre elliptische Bahn mit variabler Geschwindigkeit. Im Perihel läuft sie am schnellsten, im Aphel am langsamsten. Da der Frühlingspunkt der Sonne entgegen wandert, hat die Sonne nicht die gesamte Bahnellipse durchlaufen, wenn sie wieder auf ihn trifft: Der Zeitraum zwischen zwei Frühlingspunkt-Passagen ist daher kürzer als der Zeitraum zwischen zwei Perihel-Passagen, und zwar um die Zeitspanne, welche die Sonne für das nicht durchlaufene Bahnstück gebraucht hätte. Nun ist das eingesparte Bahnstück immer (fast) gleich groß, aber es wird nach dem Zweiten Keplerschen Gesetz mit unterschiedlichen Geschwindigkeiten durchlaufen, je nachdem, ob es sich gerade in Perihel- oder Aphelnähe befindet. Entsprechend ist die eingesparte Zeitspanne kürzer (und das so definierte tropische Jahr länger) oder länger (und das tropische Jahr kürzer) als der Mittelwert. Es dauert etwa 21.000 Jahre, bis der Frühlingspunkt vom Perihel über das Aphel wieder zum Perihel zurückgewandert ist, entsprechend unterliegt die Dauer des so definierten tropischen Jahres einer Schwankung von 21.000 Jahren Länge. Um ein mittleres tropisches Jahr zu erhalten, müsste man also über 21.000 Jahre mitteln. Darüber hinaus ist die Amplitude dieser Schwingung leicht veränderlich, da die Exzentrizität der Erdbahn ein wenig schwankt.

Gegenwärtig beträgt der zeitliche Abstand zweier Passagen durch den Frühlingspunkt (nach Abzug der oben erwähnten Schwankungen infolge Bahnstörungen) 365^d 5^h 49^m 1^s. Er nimmt um knapp 0,9 Sekunden pro Jahrhundert zu, da sich der Frühlingspunkt dem Perihel der scheinbaren Sonnenbahn nähert.

Die Länge des als Rückkehr zum präzedierenden Startpunkt definierten tropischen Jahres hängt also von der Lage des Startpunktes bezüglich des Perihels ab. Daraus folgt auch, dass insbesondere die Zeitabstände zweier Passagen durch den Herbstpunkt, durch den Sommer-Sonnwendpunkt oder den Winter-Sonnwendpunkt jeweils verschieden sind, da diese unterschiedliche Positionen bezüglich des Perihels haben. Die Tabelle zeigt die gegenwärtigen Abstände zweier Passagen durch die betreffenden Punkte (nach Abzug der Bahnstörungen):

Frühlingsanfang → Frühlingsanfang:	365^d 5^h 49^m 01^s
Sommeranfang → Sommeranfang:	365^d 5^h 47^m 57^s
Herbstanfang → Herbstanfang:	365^d 5^h 48^m 30^s
Winteranfang → Winteranfang:	365^d 5^h 49^m 33^s

Die Länge des tropischen Jahres nach dieser Definition hängt also von der willkürlichen Wahl des Frühlingspunktes als Startpunkt ab.

Präzessionsschwankungen

Als dritte Komplikation schließlich ist die Geschwindigkeit, mit der der Frühlingspunkt entlang der Ekliptik präzediert, nicht streng konstant. Die Präzession wird durch den Gravitationseinfluss von Mond, Sonne und Planeten verursacht. Die Bahnen der letzteren unterliegen aber gegenseitigen Störungen und verändern sich geringfügig (ein typisches Mehrkörper-Problem), was wiederum dazu führt, dass die Präzessionsbewegung gegenwärtig leicht beschleunigt. Dieser Effekt wird im nächsten Abschnitt näher behandelt.

Moderne Definition: Durchlaufen von 360°

Wegen der beschriebenen Unzulänglichkeiten der früheren Definition des tropischen Jahres als (mittlerer) Zeitabstand zweier Passagen der Sonne durch den Frühlingspunkt beschloss die Internationale Astronomische Union 1955 die moderne Definition:

Das tropische Jahr ist der Zeitraum, in welchem die mittlere Länge der Sonne um 360° zunimmt.

Die Länge wird dabei auf das „mittlere Äquinoktium des Datums“ bezogen, welches sich infolge der Präzession bezüglich des Fixsternhintergrunds langsam entgegengesetzt zur Sonne bewegt. Die Längenänderung von genau 360° ist also in diesem langsam – aber gleichmäßig – rotierenden Bezugssystem zu bestimmen. Gegenüber einem durch die Fixsterne definierten Bezugssystem hat die Sonne dann in der Ekliptik nur 359° 59′ 10″ zurückgelegt.

Mittlere Länge

Die ekliptikale Länge $\lambda$ eines realen Himmelskörpers auf einer elliptischen und mit variabler Geschwindigkeit durchlaufenen Bahn lässt sich für einen beliebigen Zeitpunkt $t$ berechnen, indem man zunächst die mit konstanter Geschwindigkeit $\mu$ zunehmende Länge $\lambda _{0}+\mu \cdot t$ eines fiktiven Himmelskörpers auf einer kreisförmigen Bahn gleicher Umlaufdauer bestimmt und dann durch Addieren einer relativ leicht zu berechnenden Korrektur, der so genannten Mittelpunktsgleichung, die Länge auf der elliptischen Bahn erhält. Bei höheren Genauigkeitsansprüchen sind dazu noch die durch andere Himmelskörper verursachten Bahnstörungen zu addieren. Die Mittelpunktsgleichung und die meisten Störungen sind periodische Größen. Zusätzliche Terme in $t^{2}$ , $t^{3}$ etc. berücksichtigen gegebenenfalls nichtperiodische (so genannte säkulare) Driften, welche ebenfalls durch Störungen verursacht werden:

{\lambda (t)=\lambda _{0}+\mu \cdot t+{\text{Mittelpunktsgleichung}}(t)+{\text{Störungen}}(t)+a_{1}\cdot t^{2}+a_{2}\cdot t^{3}+\dotsb }

Als mittlere Länge $\lambda _{m}$ bezeichnet man definitionsgemäß den obigen Ausdruck ohne die (weggemittelt gedachten) periodischen Terme:

{\lambda _{m}(t)=\lambda _{0}+\mu \cdot t+a_{1}\cdot t^{2}+a_{2}\cdot t^{3}+\dotsb }

Mittlere Länge der Erde

Die mittlere Länge der Erde, bezogen auf das mittlere Äquinoktium des Datums, ist gegeben durch

$\lambda _{m}(t)\,=\,$	$100{,}466.456.83^{\circ }+1.296.027.711{,}034.29''\cdot \,t\,+\,109{,}158.09''\cdot \,t^{2}\,$
	$+\,0{,}072.07''\cdot \,t^{3}\,-\,0{,}235.30''\cdot \,t^{4}\,-\,0{,}001.80''\cdot \,t^{5}\,+\,0{,}000.20''\cdot \,t^{6}$

Dabei ist $t$ die von der Epoche J2000.0 aus gerechnete Zeit in julianischen Jahrtausenden zu je 365.250 Tagen, gemessen in Terrestrischer Zeit. Ist $JDE=JD(\mathrm {TT} )$ das in Terrestrischer Zeit gezählte julianische Datum des betrachteten Zeitpunktes, so gilt:

t\,=\,(JDE\,-\,2.451.545{,}0)/365.250

.

Man beachte, dass die Koeffizienten in der Längenformel zum Teil in Grad und zum Teil in Bogensekunden gegeben sind. Die Formel ist anwendbar für die Jahre −4000 bis +8000. Sie gilt nach Addition von 180° auch für die scheinbare Bewegung der Sonne. Die nichtlinearen Terme werden hauptsächlich von der schon erwähnten Beschleunigung der Präzession erzeugt.

Das instantane tropische Jahr

Die Geschwindigkeit, mit der sich die mittlere Länge ändert, erhält man durch Ableiten nach der Zeit:

{{\frac {\mathrm {d} \lambda _{m}}{\mathrm {d} t}}(t)=1.296.027.711{,}034.29^{\frac {\mathrm {''} }{\mathrm {Jul.\,Jtsd.} }}+2\cdot 109{,}158.09^{\frac {\mathrm {''} }{\mathrm {Jul.\,Jtsd.} ^{2}}}\cdot t+3\cdot 0{,}072.07^{\frac {\mathrm {''} }{\mathrm {Jul.\,Jtsd.} ^{3}}}\cdot t^{2}+\dotsb }

Am 1. Januar des Jahres 2000 um 12 Uhr Terrestrischer Zeit, also für $t=0$ , änderte sich die mittlere Länge der Sonne mit einer Geschwindigkeit von

\left.{\frac {\mathrm {d} \lambda _{m}}{\mathrm {d} t}}\right|_{t=0}=1.296.027.711{,}034.29^{\frac {\mathrm {''} }{\mathrm {Jul.\,Jtsd.} }}

Um mit dieser Geschwindigkeit eine Strecke von 360° = 1.296.000″ zurückzulegen, brauchte sie (unter gleichzeitiger Umrechnung von julianischen Jahrtausenden in Tage)

${D_{\mathrm {tr} }}\,$	$\,=\,{\frac {1.296.000^{\mathrm {''} }}{1.296.027.711{,}034.29^{\frac {\mathrm {''} }{\mathrm {Jul.\,Jtsd.} }}}}\cdot 365.250^{\frac {\mathrm {d} }{\mathrm {Jul.\,Jtsd.} }}$
	$\,=\,365{,}242.190.402.11^{\mathrm {d} }=365^{\mathrm {d} }\,5^{\mathrm {h} }\,48^{\mathrm {m} }\,45{,}250.742^{\mathrm {s} }$

(Ein neuerer Wert beträgt 365^d 5^h 48^m 45,261^s für den Beginn des Jahres 2000.)

Man beachte, dass dies der Zeitraum ist, den die Sonne unter Beibehaltung der Geschwindigkeit vom 1. Januar 2000 brauchte, um 360° zurückzulegen. Es ist nicht der Zeitraum, nach dem sie tatsächlich 360° zurückgelegt hat (dieser würde lediglich 365^d 5^h 48^m 45,248.085^s betragen), denn während dieses Jahres hat sich ihre Geschwindigkeit ja wegen der säkularen Terme geringfügig erhöht. Die oben berechnete Jahreslänge ist lediglich eine andere Ausdrucksweise für die Geschwindigkeit, mit der sich die mittlere Länge der Sonne zu einem bestimmten Zeitpunkt ändert; es handelt sich um die so genannte instantane Jahreslänge. Das ist vergleichbar mit der Angabe, ein Fahrzeug bewege sich im Augenblick (instantan) mit einer Geschwindigkeit von 100 Kilometern pro Stunde. Man muss, um diese Angabe machen zu können, nicht warten, bis das Fahrzeug tatsächlich 100 km zurückgelegt hat. Gemeint ist vielmehr: es würde für 100 Kilometer eine Stunde brauchen, wenn es die gegenwärtige Geschwindigkeit unverändert beibehielte. Für eine reale Reisestrecke von 100 km kann es auch weniger als eine Stunde brauchen, wenn die Geschwindigkeit während der Fahrt zunimmt. Dementsprechend wurde eingangs die Jahreslänge für den „Beginn des Jahres 2000“ angegeben, nicht als Länge des Jahres 2000 selbst.

Da beim Übergang zur mittleren Länge der periodische Einfluss der Bahnelliptizität „weggemittelt“ wurde und ohnehin nur die momentane Geschwindigkeit betrachtet wird, spielt es für die Definition keine Rolle mehr, an welcher Stelle der Bahn der Startpunkt liegt. Die moderne Definition ist also unabhängig vom Frühlingspunkt.

Veränderlichkeit des tropischen Jahres

Im vorigen Abschnitt wurde die Länge des tropischen Jahres speziell für den Zeitpunkt des 1. Januar 2000 abgeleitet, indem die Geschwindigkeit, mit der sich die mittlere Länge ändert, für den Sonderfall $t=0$ berechnet wurde. Behalten wir stattdessen den allgemeinen Ausdruck für ${\tfrac {\mathrm {d} \lambda _{m}}{\mathrm {d} t}}(t)$ bei, so ist die instantane tropische Jahreslänge $D_{tr}$ für einen beliebigen Zeitpunkt $t$ gegeben durch

$D_{\mathrm {tr} }(t)\,$	$=\,{\frac {1.296.000^{''}}{{\frac {\mathrm {d} \lambda _{m}}{\mathrm {d} t}}(t)}}$
	$=\,{\frac {1.296.000^{''}}{1.296.027.711{,}034.29^{\frac {\mathrm {''} }{\mathrm {Jul.\,Jtsd.} }}+\,2\cdot 109{,}158.09^{\frac {\mathrm {''} }{\mathrm {Jul.\,Jtsd.} ^{2}}}\cdot \,t\,+\dotsb }}$ .

Ist eine Potenzreihe

S\,=\,a+bx+cx^{2}+dx^{3}+\dotsb

gegeben, so lässt sich ihr Reziprokes $1/S$ ebenfalls in eine Potenzreihe entwickeln, und es ist

{\frac {1}{S}}\,=\,{\frac {1}{a}}\,-\,{\frac {b}{a^{2}}}x\,+\,\left({\frac {b^{2}}{a^{3}}}-{\frac {c}{a^{2}}}\right)x^{2}\,+\,\left({\frac {2bc}{a^{3}}}-{\frac {d}{a^{2}}}-{\frac {b^{3}}{a^{4}}}\right)x^{3}\,+\,\dotsb

.

Für obigen Ausdruck folgt damit als Jahreslänge (unter gleichzeitiger Umrechnung von julianischen Jahrtausenden in Tage):

$\,D_{\mathrm {tr} }(t)\,$	${=365{,}242.190.402.11-6{,}152.513.5\cdot 10^{-5}\cdot t-6{,}093\cdot 10^{-8}\cdot t^{2}+\dots \quad {\text{Tage}}}$
	${=365^{\mathrm {d} }\,5^{\mathrm {h} }\,48^{\mathrm {m} }\,45{,}250.742^{\mathrm {s} }-(5{,}315.771.7\cdot t)\,\mathrm {s} -(0{,}005.264\cdot t^{2})\mathrm {s} +\dots }$

Die instantane Länge des tropischen Jahres betrug also am 1. Januar 2000 365^d 5^h 48^m 45,250.742^s, am 1. Juli 2000 365^d 5^h 48^m 45,248.093^s und am 31. Dezember 2000 365^d 5^h 48^m 45,245.415^s. Der Zeitraum, den die Sonne brauchte, um – am 1. Januar bei 0° startend – insgesamt 360° zurückzulegen, betrug 365^d 5^h 48^m 45,248.085^s; das ist der Mittelwert der instantanen Jahreslängen, die im Verlaufe dieses Zeitraums auftraten. Dies ist vergleichbar mit der Tatsache, dass die Fahrdauer, die ein Fahrzeug für eine bestimmte Strecke braucht, sich aus dem Mittelwert über seine im Verlaufe der Strecke gefahrenen Momentangeschwindigkeiten ergibt. In beiden Fällen ist die benötigte Gesamtzeit das Reziproke des Mittelwerts über die Momentangeschwindigkeiten.

In all diesen Formeln ist unter Tag der idealisierte und stets gleich lange Ephemeridentag zu je 86.400 Sekunden zu verstehen. Für die Frage, wie viele reale Erdumdrehungen bzw. wie viele mittlere Sonnentage auf ein tropisches Jahr entfallen, wären zusätzlich die Schwankungen und die langfristige Verlangsamung der Erdrotation zu berücksichtigen (s. u.).

Die instantane Länge des tropischen Jahres am 0. Januar 1900 (= 31. Dezember 1899) 12h UT diente als Grundlage für die Definition der Ephemeridensekunde, des Vorläufers der heutigen, atomphysikalisch definierten Sekunde (des Internationalen Einheitensystems).

Die Länge des tropischen Jahres ändert sich, weil die Präzessionsbewegung des als Bezugsrichtung dienenden Frühlingspunktes gegenwärtig geringfügig beschleunigt. Die Länge des auf den Fixsternhintergrund bezogenen siderischen Jahres unterliegt hingegen lediglich kurzfristigen periodischen Schwankungen, aber keiner langfristigen Veränderung.

Vergleich der Definitionen

Vergleich der verschiedenen Definitionen für das tropische Jahr

Die nebenstehende Illustration zeigt zum Vergleich die Längen der tropischen Jahre unterschiedlicher Definition über eine Zeitspanne von 16 Jahrtausenden hinweg.

Die farbigen Kurven stellen jeweils den Zeitraum dar, den die Sonne braucht, um nach einem vollen Umlauf zum selben Referenzpunkt auf der Ekliptik zurückzukehren, und zwar für die Referenzpunkte Frühlingsäquinoktium, Sommersonnwende, Herbstäquinoktium und Wintersonnwende. Wie deutlich zu erkennen ist, hängt dieser Zeitraum von der Wahl des Referenzpunktes ab, durchläuft aber jeweils vergleichbare Schwingungen mit einer Amplitude von knapp einer Minute und einer Periodenlänge von etwa 21.000 Jahren (nach welcher die präzedierenden Referenzpunkte wieder dieselbe Stellung bezüglich des Perihels einnehmen).

Die graue Kurve zeigt die Länge des tropischen Jahres nach der 360°-Definition. Sie ist unabhängig von Referenzpunkten und weist nur eine geringe Schwankung mit recht langer Periode auf, welche mit Ungleichförmigkeiten der Präzession zusammenhängt.

Historische Entwicklung der Messung

Jahr	Verwendung	Jahreslänge
	Babylon	365^d 4^h 365^d 6^h 36^m
432 v. Chr.	Metonischer Kalender	365^d 6^h 19^m
	Kallippischer Kalender	365^d 6^h
200 v. Chr.	Ptolemäus	365^d 5^h 55^m
882	al-Battani	365^d 5^h 46^m 24^s
1252	Alfons X.	365^d 5^h 49^m 16^s
1551	Prutenische Tafeln	365^d 5^h 55^m 58^s
1627	Rudolfinische Tafeln	365^d 5^h 48^m 45^s
	Jérôme Lalande	365^d 5^h 48^m 45,5^s

Die Erkenntnis, dass sich die Sonnenstände und damit die Jahreszeiten im Rhythmus von etwa 365 Tagen wiederholen, stammt aus prähistorischen Zeiten. Leider sind aus den älteren Kulturen allenfalls sehr vage Angaben über ihre Kenntnis der Jahreslänge überliefert.

In der babylonischen Astronomie gab es keinen allgemein verbindlichen Zahlenwert für die in Tagen ausgedrückte Länge des Jahres. Die in verschiedenen astronomischen Berechnungssystemen verwendeten Parameter entsprechen Jahreslängen zwischen 365^d 4^h und 365^d 6,6^h.

Der griechische Astronom Meton führte im Jahr 432 v. Chr. in Athen einen auf dem metonischen Zyklus beruhenden Kalender ein, der einer Jahreslänge von 365 1/4 + 1/76 Tagen entsprach. Hundert Jahre später modifizierte Kallippos diesen Zyklus, indem er jeweils einen Tag in vier Metonischen Zyklen fortließ und so den kallippischen Zyklus erhielt, der einer Jahreslänge von 365 1/4 Tagen entsprach.

Die früheste überlieferte Beschreibung einer Bestimmung der Jahreslänge stammt von Ptolemäus, der im Almagest die von Hipparch im 2. Jh. v. Chr. benutzten Methoden und Beobachtungen aufführte. Auf Hipparchs Entdeckung der Präzession geht auch die Unterscheidung zwischen siderischem und tropischem Jahr zurück. Unter letzterem verstand Hipparch den Zeitraum zwischen zwei entsprechenden Äquinoktien oder Solstitien. Hipparch bestimmte die Zeitpunkte einiger Äquinoktien und Solstitien und verglich sie mit Beobachtungen, die Meton und Euktemon (5. Jh. v. Chr.) und Aristarch (3. Jh. v. Chr.) angestellt hatten. Er erhielt 365 1/4 − 1/300 Tage für das tropische Jahr, das entspricht etwa 365^d 5^h 55^m, während der tatsächliche Wert damals 365^d 5^h 49^m 9^s betrug.

Hipparch hatte noch Zweifel geäußert, ob das tropische Jahr wirklich eine konstante Länge habe. Ptolemäus (2. Jh. n. Chr.) bestimmte die Jahreslänge erneut mit derselben Methode, erhielt exakt dasselbe Ergebnis und sah keinen Grund, an der Konstanz der Jahreslänge zu zweifeln.

Im Jahr 882 beobachtete al-Battani die Herbst-Tagundnachtgleiche und erhielt aus dem Vergleich mit einer von Ptolemäus überlieferten Beobachtung eine Jahreslänge von 365^d 14' 26" (in sexagesimaler Notation), das entspricht etwa 365^d 5^h 46^m 24^s. (Für andere Beispiele der zahlreichen Jahreslängenbestimmungen während der Arabischen Periode der Astronomie siehe Al Sufi, Ulug Beg.)

Gegen Ende des Mittelalters waren Ungenauigkeiten in den Planetentafeln des Almagest und ihrer arabischen Nachfolger zu erheblichen Fehlern angewachsen, so dass eine Überarbeitung der Tafeln notwendig wurde. Das Ergebnis waren die 1252 veröffentlichten Alfonsinischen Tafeln. Diese Tafeln benutzten eine Jahreslänge von 365^d 5^h 49^m 16^s.

Im Jahr 1551 erschienen die von Erasmus Reinhold erarbeiteten Prutenischen Tafeln, die auf der heliozentrischen Planetentheorie von Nikolaus Kopernikus beruhten. Dazu verbesserte Reinhold die ursprünglich von Kopernikus angegebenen Zahlenwerte und benutzte eine Jahreslänge von 365^d 5^h 55^m 58^s.

Schließlich veröffentlichte Johannes Kepler im Jahr 1627 seine Rudolphinischen Tafeln. Er hatte eigene Beobachtungen mit denen des Astronomen Bernhard Walther verglichen und eine Jahreslänge von 365^d 5^h 48^m 45^s erhalten.

Während der nächsten Jahrhunderte befasste sich beinahe jeder Astronom auch mit der Bestimmung der Jahreslänge. So fand beispielsweise Jérôme Lalande (1732–1807) 365^d 5^h 48^m 45,5^s. Mit Lalande begann man auch, den himmelsmechanischen Komplikationen bei der Bestimmung der Jahreslänge Aufmerksamkeit zu schenken, nämlich der Bewegung des Perihels, der säkularen Beschleunigung der Präzession und den hauptsächlich durch den Mond sowie Venus und Jupiter verursachten Bahnstörungen. Es war mittlerweile klar geworden, dass die Zeitpunkte einzelner Äquinoktien oder Solstitien wegen dieser Einflüsse Schwankungen von mehreren Minuten unterliegen und die bloße Messung ihrer Zeitabstände daher je nach verwendeten Beobachtungspaaren zu unterschiedlichen Ergebnissen führen musste.

Erst als die analytische Himmelsmechanik im 18. Jh. weit genug entwickelt war, um die Feinheiten der mittleren Bewegung der Sonne und ihre zeitliche Veränderlichkeit aus der Gravitationstheorie abzuleiten, konnte das tropische Jahr auf eine von periodischen Störungen unabhängige Weise definiert werden. Lediglich die durch die Beschleunigung der Präzession verursachte säkulare Verkürzung des tropischen Jahres wurde als eine Eigenschaft desselben definiert und nicht herausgerechnet; das tropische Jahr wurde also als langfristig veränderlich betrachtet.

So gab J. H. von Mädler im Jahre 1840 die (damals) gegenwärtige Länge des tropischen Jahres als 365^d 5^h 48^m 47,5711^s mit einer Abnahme von 0,595 s pro Jahrhundert an.

U.J.J. LeVerrier beschrieb die momentane Länge des tropischen Jahres und seine Veränderlichkeit durch

365^{\mathrm {d} }\,5^{\mathrm {h} }\,48^{\mathrm {m} }\,45{,}775^{\mathrm {s} }-(0{,}539\cdot T)\,\mathrm {s}

,

und S. Newcomb erhielt aus seiner Sonnentheorie

365^{\mathrm {d} }\,5^{\mathrm {h} }\,48^{\mathrm {m} }\,46{,}0^{\mathrm {s} }-(0{,}530\cdot T)\,\mathrm {s} .

In den beiden letzten Ausdrücken ist $T$ die vom Zeitpunkt 1900 Januar 0,5 Ephemeridenzeit an gemessene Zeit in julianischen Jahrhunderten zu je 36525 Tagen.

Gemäß der Planetentheorie VSOP 87 beträgt die Länge des tropischen Jahres

365^{\mathrm {d} }\,5^{\mathrm {h} }\,48^{\mathrm {m} }45{,}183.4^{\mathrm {s} }-(5{,}315.5\cdot t)\,\mathrm {s} -(0{,}005.26\cdot t^{2})\,\mathrm {s} +(0{,}022.917\cdot t^{3})\,\mathrm {s}

.

Hier wird $t$ in julianischen Jahrtausenden zu je 365250 Tagen seit der Epoche J2000.0 gemessen. Ein Tag ist in den letzten drei Formeln jeweils ein Ephemeridentag, dessen Länge einem mittleren Sonnentag etwa um das Jahr 1820 entspricht. Die langsame Zunahme der Tageslänge wäre zusätzlich zu berücksichtigen (siehe nächsten Abschnitt).

Tropisches Jahr und Kalenderjahr

Kalender dienen der Zeitrechnung, jedoch mit sehr unterschiedlichen Zielsetzungen (z. B. zur Festlegung religiöser Feste, für landwirtschaftliche Planungen usw.) und mit sehr verschiedenen Verfahren (auf reiner Beobachtung beruhend, auf nichtastronomischen mathematischen Zyklen beruhend, auf astronomisch abgeleiteten mathematischen Zyklen beruhend usw.). Zahlreiche Kalender versuchen die Abfolge der Jahreszeiten nachzuvollziehen, indem sie mit Hilfe einer arithmetisch formulierten Schaltregel die Länge des tropischen Jahres durch eine geeignete Abfolge von verschieden langen, aber jeweils ganze Tage enthaltenden Kalenderjahren annähern. Beim Vergleich solcher Schaltregeln mit dem astronomischen tropischen Jahr sind die oben erwähnten unterschiedlichen Definitionen zu beachten.

Im gregorianischen Kalender hat das Kalenderjahr im Mittel eine Länge von 365 + 1/4 − 1/100 + 1/400 = 365,242.5 Tagen. Um den Fehler der gregorianischen Schaltregel zu bestimmen, wird diese Zahl oft mit der aus Tabellenwerken entnommenen Länge des tropischen Jahres von 365,242.19… Tagen verglichen. Die Differenz beträgt 0,000.31 Tage pro Jahr oder einen Tag nach etwa 3200 Jahren. Nach dieser Zeitspanne, so die übliche Argumentation, werde der gregorianische Kalender um einen Tag vom tropischen Jahreslauf abweichen. Dabei sind jedoch die Veränderlichkeit der tropischen Jahreslänge und die Frage nach der zu verwendenden Definition des tropischen Jahres nicht berücksichtigt.

Tropische und gregorianische Jahreslängen, gemessen in Ephemeridentagen

Die angeführte Argumentation stützt sich auf den heute gängigen Zahlenwert, welcher der 360°-Definition des tropischen Jahres entspricht. Wie oben erläutert, nimmt die Länge dieses tropischen Jahres jedoch um etwa 0,5 Sekunden pro Jahrhundert ab (graue Kurve im nebenstehenden Bild). Das tropische Jahr, das ohnehin bereits kürzer ist als das gregorianische Kalenderjahr, wird im Verlaufe der folgenden Jahrhunderte noch kürzer, so dass der Fehler rascher als erwartet anwächst.

Papst Gregor XIII. hatte allerdings nach eigenen Worten die neue Schaltregel eingeführt, „damit in Zukunft das Frühlingsäquinoktium nicht wieder vom 21. März abweiche“ (ne in posterum a xii. Cal. April. aequinoctium recedat). Demnach soll das Kalenderjahr dem Zeitraum zwischen zwei Durchgängen der Sonne durch den Frühlingspunkt und damit der früheren Definition des tropischen Jahres entsprechen. Dieser Zeitraum beträgt gegenwärtig 365,242.375 Tage (vgl. Tabelle weiter oben) und nimmt zu (grüne Kurve im nebenstehenden Bild). Der Fehler von gegenwärtig nur 0,000.125 Tagen pro Jahr wird also künftig weiter abnehmen, und über mehrere Jahrtausende hinweg wird das gregorianische Kalenderjahr eine exzellente Annäherung an das tropische Jahr in der traditionellen Definition sein.

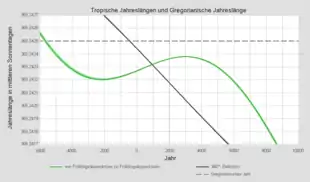
Tropische und gregorianische Jahreslängen, gemessen in mittleren Sonnentagen

Nicht berücksichtigt wurde bisher die geringfügige, aber kontinuierliche Verlangsamung der Erdrotation. Der Kalender zählt die realen Tag-Nacht-Wechsel, also die im Laufe der Jahrhunderte länger werdenden mittleren Sonnentage. Den oben angegebenen Formeln für die Länge der tropischen Jahre liegen jedoch konstante Ephemeridentage zu je 86.400 Sekunden zugrunde. Werden die tropischen Jahre stattdessen ebenfalls in mittleren Sonnentagen gemessen, so ergibt sich zusätzlich zu den bisher beschriebenen Veränderlichkeiten der Jahreslänge eine kontinuierliche scheinbare Verkürzung der Jahre (weil sich die nun verwendete Zeiteinheit ständig dehnt). Das zweite Bild zeigt die Auswirkung auf die Jahreslängen, wobei gemäß aktuellen Untersuchungen angenommen wurde, dass die Tageslänge langfristig um 1,7 ± 0,05 Millisekunden pro Jahrhundert zunimmt. Der Unterschied zwischen Kalenderjahr und 360°-Jahr nimmt nun noch schneller zu. Der Unterschied zwischen Kalenderjahr und Frühlingspunktsjahr nimmt nach wie vor in nächster Zeit weiter ab, wird jedoch bereits um das Jahr 3000 mit ca. 0,000.12 Tagen pro Jahr ein Minimum erreichen, um dann wieder zuzunehmen.

Für die Schaltregeln anderer Kalender siehe den Artikel Schaltjahr.

Siehe auch

Literatur

K. M. Borkowski: The Tropical Year and Solar Calendar. In: J. Roy. Astron. Soc. Can. Band 85, Nr. 3, 1991, bibcode:1991JRASC..85..121B
J. Meeus, D. Savoie: The history of the tropical year. In: J. Br. Astron. Assoc. Band 102, Nr. 1, 1992, bibcode:1992JBAA..102...40M

Einzelnachweise

Definitionen:

Definitionen: (Meeus 2002), S. 359
Tabelle, Abstand zweier Frühlingsanfänge: berechnet aus den Äquinoktien in (Meeus 1995)
Tabelle, Dauer der Äquinoktial- und Solstitialjahre: (Meeus 2002), S. 362
Neudefinition geschah durch IAU 1955: (Seidelmann 1992), S. 80
Formel für mittlere Länge der Erde: (Meeus 2002), S. 360; Originalquelle: (Simon 1994)
Neuerer Wert 365^d 5^h 48^m 45,261^s: (Bretagnon, Rocher 2001)
Potenzreihenentwicklung des Reziproken einer Potenzreihe: (Bronstein 1993)
Grafik, Vergleich verschiedener Definitionen: nach Bahnelementen aus (Meeus 2002), Kap. 63; Originalquelle (Simon 1994). Die 360°-Kurve ist das Reziproke der instantanen Geschwindigkeit der mittleren Länge der Sonne, ausgedrückt in Ephemeridentagen pro 360°. Die anderen Kurven sind die Zeitintervalle, ausgedrückt in Ephemeridentagen, welche die ekliptikale Länge der Sonne (berechnet aus den genannten mittleren Bahnelementen) für einen vollen Umlauf braucht, jeweils für Start- und Zielpunkt Frühlingsäquinoktium, Sommersonnwende, Herbstäquinoktium und Wintersonnwende.

Historische Entwicklung der Messung:

Geschichte: hauptsächlich (Meeus 1992)
Babylonische Jahreslängen: (Neugebauer 1975), S. 528
Meton, Kallippos, Hipparch, Ptolemäus: (Ptolemäus 0150), S. 12, 131 ff.
al-Battani: (al-Battani 900), S. 42
Mädler: (Mädler 1852), S. 147

Tropisches Jahr und gregorianischer Kalender:

Tropisches Jahr und Gregorianischer Kalender: (Meeus 2002), Kap. 63
Zitat Gregor XIII: (GregorXIII 1581)
Zunahme der Tageslänge 1,7 ± 0,05 Millisekunden pro Jahrhundert: (Stephenson 1997), S. 514

Verwendete Quellen:

(al-Battani 900): al-Battani, M.: Zij. Ar-Raqqah, ca. 900; lat. Übersetzung: C. A. Nallino: Al-Battani sive Albatenii Opus Astronomicum. Mailand 1899–1907; Nachdruck Olms, Hildesheim 1977
(Bretagnon, Rocher 2001): Bretagnon, P., Rocher, P.: Du Temps universel au Temps coordonnée barycentrique. Découverte, No. 285, S. 39–47 (2001)
(Bronstein 1993): Bronstein, I. N., Semendjajew, K.A., Musiol, G., Mühlig, H.: Taschenbuch der Mathematik. Harri Deutsch, Frankfurt/M. 1993, ISBN 3-8171-2001-X
(GregorXIII 1581): Gregor XIII: Bulle Inter Gravissimas, Tusculum 1581 (Online-Quelle, aufgerufen 10. Juli 2006)
(Mädler 1852): Mädler, J. H.: Populäre Astronomie. Carl Heymann, Berlin 1852
(Meeus 1992): Meeus, J., Savoie, D.: The history of the tropical year, siehe Literatur
(Meeus 1995): Meeus, J.: Astronomical Tables of the Sun, Moon and Planets. Willmann-Bell, Richmond 1995, ISBN 0-943396-45-X
(Meeus 2002): Meeus, J.: More Mathematical Astronomy Morsels. Willmann-Bell, Richmond 2002, ISBN 0-943396-74-3
(Neugebauer 1975): Neugebauer, O.: A History of Ancient Mathematical Astronomy. Springer, Berlin 1975, ISBN 3-540-06995-X
(Ptolemäus 0150): Ptolemäus, C.: Almagest. Alexandria, ca. 150; engl. Übersetzung: G. J. Toomer (Übers.): Ptolemy’s Almagest, Princeton University Press, Princeton 1998, ISBN 0-691-00260-6
(Seidelmann 1992): Seidelmann P. K. (Hrsg.): Explanatory Supplement to the Astronomical Almanac. University Science Books, Mill Valley 1992, ISBN 0-935702-68-7
(Simon 1994): Simon, J. L. et al.: Numerical expressions for precession formulae and mean elements for the Moon and the planets, Astronomy and Astrophysics, vol. 282, S. 663–683 (1994) (bibcode:1994A&A...282..663S)
(Stephenson 1997): Stephenson, F. R.: Historical Eclipses and Earth’s Rotation, Cambridge University Press, Cambridge 1997, ISBN 0-521-46194-4

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.