Ekliptik
Die Ekliptik ist die scheinbare Bahn der Sonne durch den Fixsternhimmel, wie sie von der Erde aus im Laufe eines Jahres gesehen wird. Zuweilen wird auch die Ekliptikebene, also die Ebene, in der die scheinbare Sonnenbahn liegt, als Ekliptik bezeichnet. Auch der Mond und alle Planeten liegen bis auf wenige Grad Abweichung auf der Ekliptik. Auf der Himmelskugel ist die Ekliptik ein Großkreis.
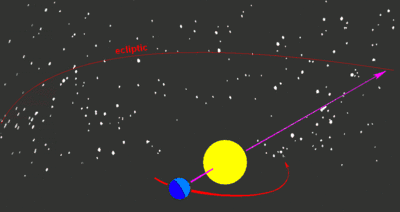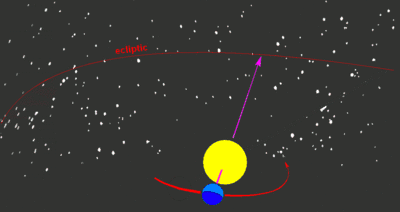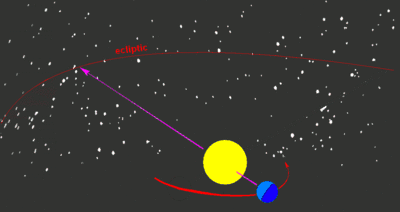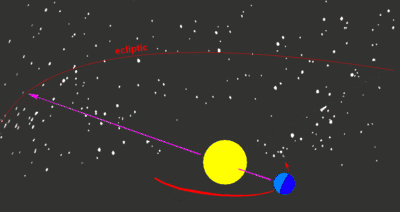
Die Ekliptik wurde bereits im frühen Altertum entdeckt. Zwar nicht am Tag, aber in der Dämmerung ist die Position der Sonne auf dem Hintergrund der Sterne zu erkennen. Die Sonne durchläuft im Jahr eine feste Abfolge von 12 Sternbildern (nach antiker Einteilung) bzw. 13 Sternbildern (nach heutiger Einteilung). Eine etwa 20 Grad breite Zone um die Ekliptik heißt Tierkreis. Die Tierkreiszeichen sind nach den 12 antiken Sternbildern des Tierkreises benannt.
Der nördliche und der südliche Ekliptikpol sind die beiden Schnittpunkte der Himmelskugel mit einer Geraden, die durch den Erdmittelpunkt geht und senkrecht auf der Ekliptikebene steht.
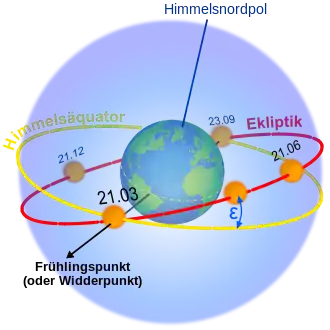

Die Ebene der Ekliptik liegt nicht in der Ebene des Erdäquators, der durch die tägliche Rotation der Erde um die eigene Achse festgelegt ist, sondern ist um einen Winkel von ca. 23,5° verkippt. Dieser Winkel heißt Schiefe der Ekliptik und gibt auch den Winkelabstand der Ekliptikpole von den Himmelspolen an. Vom Polarstern ausgehend liegt der nördliche Ekliptikpol etwa im selben Abstand wie das Sternbild Großer Wagen, aber im Sternbild Drache.
Die vom Erdmittelpunkt aus gedachte Projektion des Erdäquators auf die Himmelskugel heißt Himmelsäquator. Die Ebene der Ekliptik wird also durch die jährliche Bahn der Erde um die Sonne bestimmt, die Ebene des Äquators durch die tägliche Rotation der Erde um die eigene Achse.
Etymologie
Der Name Ekliptik (lat. linea ecliptica‚ der Eklipse zugehörende Linie‘) für die scheinbare Bahn der Sonne ist abgeleitet von dem griechischen Ausdruck ἐκλειπτική [τροχιά] ekleiptikē [trochiá] für ‚verdeckende [Umlaufbahn]‘ (zu ἔκλειψις ékleipsis ‚Verlassen, Ausbleiben, (Sonnen-/Mond-)Finsternis‘), denn schon im Altertum war bekannt, dass sich eine Mondfinsternis nur ereignet, wenn der Mond die Sonnenbahn kreuzt.
Einführung
Die Sonne beschreibt am Himmel zwei unterschiedliche scheinbare Bahnen:
- Infolge der Rotation der Erde um ihre eigene Achse scheint der Fixsternhimmel und vor ihm die Sonne im Laufe eines Tages von Ost nach West um die Erde zu rotieren. Dies führt zur scheinbaren täglichen Bewegung der Sonne relativ zum Horizont, dem Tagbogen.
- Als Folge des jährlichen Umlaufs der Erde um die Sonne verschiebt sich dabei allmählich die Stellung der Sonne in Bezug auf den Fixsternhimmel. Sie durchläuft in einem Jahr die 12 (antiken) bzw. 13 (modernen) Sternbilder des Tierkreises.
Die Bahn der jährlichen scheinbaren Bewegung der Sonne relativ zum Fixsternhimmel ist die Ekliptik. Ihr Verlauf lässt sich z. B. darstellen, indem man die im Laufe eines Jahres ermittelten Positionen der Sonne auf einem Himmelsglobus vermerkt. Dabei spielt es praktisch keine Rolle, von welchem Ort der Erde aus die Beobachtungen durchgeführt werden, da die Sonne im Verhältnis zur Größe der Erde sehr weit entfernt ist und der Beobachtungswinkel somit nahezu gleich bleibt.
Die Ekliptikebene

Heliozentrisch betrachtet umläuft die Erde die Sonne auf einer in der Ekliptikebene liegenden Bahn.
Bei genauerer Betrachtung ist es nicht die Erde, die auf dieser Bahn um die Sonne läuft, sondern der gemeinsame Schwerpunkt von Erde und Mond (der noch im Innern der Erde, aber nicht in ihrem Zentrum liegt). Daher wandert die Sonne geozentrisch gesehen nicht exakt auf der Ekliptik über den Himmel, sondern ihre ekliptikale Breite schwankt im Monatsrhythmus um etwa ±0,7″ um den Mittelwert 0.
Die Ekliptikebene dient als Bezugsebene für Ortsangaben im Sonnensystem (ekliptikales Koordinatensystem).
Die Schiefe der Ekliptik
Die Erdachse, die Rotationsachse der Erde, steht nicht senkrecht auf der Ebene der Erdbahn, sondern bildet mit ihr einen Winkel von zurzeit 66,56359°. Dadurch schließt die Ebene des Äquators der Erde bzw. des Himmelsäquators mit der ekliptikalen Ebene derzeit einen Winkel von 23,43641° (23° 26′ 11.08″) ein, der Schiefe der Ekliptik oder Obliquität genannt wird (lat. obliquus ‚schief‘).
Die Bezeichnung Erdneigung gibt diesen Winkel unter dem Blick von der Ekliptikebene auf die Erde wieder, der Perspektive des Ekliptikalen Koordinatensystems.
Die Schiefe der Ekliptik ist eine der zehn wichtigsten Basisgrößen der Astronomie und Geodäsie zur Definition von Koordinatensystemen und für Berechnungen. Sie wird meist mit dem griechischen Buchstaben ε (epsilon) bezeichnet. Durch die Gravitationseinflüsse der anderen Körper im Sonnensystem ändert sie sich langperiodisch: sie variiert innerhalb von rund 40.000 Jahren etwa zwischen 21° 55′ und 24° 18′, also um über 2°.
Die Jahreszeiten
Während die Erde die Sonne umläuft, bleibt die Richtung ihrer Achse im Raum fast unverändert, wenn man von den oben beschriebenen langperiodischen Effekten absieht. Dadurch ist von März bis September die Nordhalbkugel etwas mehr zur Sonne hin geneigt, von September bis März die Südhalbkugel. Im Jahreslauf ändern sich daher der Einfallswinkel der Sonnenstrahlen und die Dauer des lichten Tages, womit die Jahreszeiten entstehen.
Der Tierkreis

Während die Bahn der Erde in der Ekliptikebene liegt und die Sonne von der umlaufenden Erde aus gesehen jährlich eine Bahn längs der Ekliptik zu durchlaufen scheint, sind die Bahnebenen des Mondes und der anderen Planeten gegenüber der Ekliptikebene verschieden leicht geneigt. Deren scheinbare Bahnen verlaufen daher innerhalb eines einige Grad breiten Streifens um die Ekliptik, dem Zodiak oder Tierkreis. Seit der Antike wird dieser vom Frühlingspunkt aus nach Osten in zwölf gleich große Abschnitte unterteilt (zu je 360°/12 = 30°), denen Zeichen des Tierkreises zugeordnet sind. Diese haben ihre Namen zwar von den Ekliptiksternbildern, doch stimmen sie in ihrer Lage nicht mehr mit denen überein. In der Astrologie werden die Positionen von Sonne, Mond und Planeten bezogen auf die Tierkreiszeichen beschrieben.
Die Präzession
Die beiden Ekliptikpole bilden die Mittelpunkte zweier Kreise, auf denen sich der nördliche bzw. südliche Himmelspol im Laufe eines Platonischen Jahres von rund 26.000 Jahren infolge der Präzession der Erdachse bewegt.
Da die Gestalt der Erde von einer Kugel abweicht (Erdellipsoid), bewirken die Gezeitenkräfte von Mond und Sonne ein Drehmoment, das die schrägstehende Erdachse aufzurichten versucht und dabei deren Richtung ändert. Wie bei einem schräglaufenden Kreisel beschreibt die Erdachse, deren Verlängerung die beiden Himmelspole zeigt, daher eine Präzessionsbewegung und wandert auf einem Kegelmantel mit Öffnungswinkel 2ε um die Ekliptikpole. Auf präziseren Sternkarten sind diese Ekliptikpole eingezeichnet – der nördliche befindet sich im Sternbild Drache, definitionsgemäß auf Rektaszension 18 h (mit einer Deklination von 90°−ε, z. Z. rund 66° 34′), der südliche im Sternbild Schwertfisch auf 6 h.
Der „Erdkreisel“ ist wegen der großen Erdmasse von knapp 6·1024 kg sehr träge, die Erdachse braucht für einen Zyklus der Präzession etwa 25.700–25.800 Jahre (Platonisches Jahr). Der heutige Polarstern nimmt seine Rolle also nur vorübergehend ein.
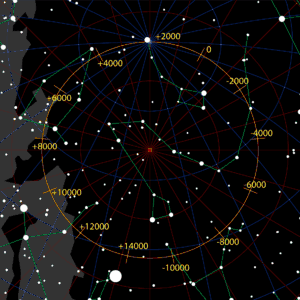 Der Weg (orange) des Himmelsnordpols um den Ekliptikpol (rot), wofür er etwa 26.000 Jahre benötigt; um das Jahr (+)2000 ist er nahe dem Polarstern. Der sehr helle Stern unten ist die Wega. |
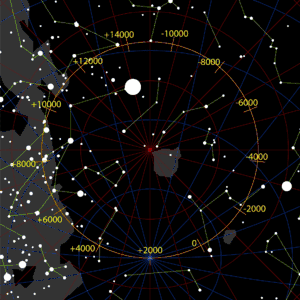 Der Weg des Himmelssüdpols um den Ekliptikpol, wofür er etwa 26.000 Jahre benötigt. Um das Jahr (+)2000 liegt er nahe bei Polaris Australis. Der überaus helle Stern auf dem Bild ist Canopus. |
Geschichte
Für die frühen Astronomen war die am Nachthimmel unmittelbar zu beobachtende Bahn des Mondes und die Auf- und Untergänge der Sterne mit der größten Leuchtkraft offensichtlich; den Zusammenhang von Ekliptik und scheinbarer Bahn der Sonne erkannte man noch nicht.[1] Allerdings wurden, angeregt durch Sonnen- und Mondfinsternisse, die von der Position des Mondes im Bezug auf die Ekliptikbahn abhängig sind, entsprechende Mythen entwickelt. Die frühe chinesische Astronomie spricht von einem himmlischen Drachen, der Mond und Sonne verschlingt.[2] Die frühe Indische Astronomie kennt den Dämonen Rahu, der beide Gestirne verschlingt.[3] Solche und ähnliche Mythen führten zur Bezeichnung Drachenpunkte für die Mondknoten.
Die altägyptischen Vorstellungen des Himmels bezogen sich dagegen mit mythologischem Hintergrund unter anderem auf Dekan-Sterne und orientierten sich an deren heliakischer Sichtung. Erst in der hellenistischen Zeit wurde das in Mesopotamien entwickelte Konzept des Zodiaks aufgenommen.[4] Dort hatte die Beobachtung der Gestirne schon im Altbabylonischen Reich eingesetzt. Aber erst in der Assyrischen Zeit (1200–630 v. Chr.) wurden Vorstellungen entwickelt, die der Ekliptik nahestehen. So findet sich in der Datensammlung der MUL-apin-Texte die Idee der vier Jahreszeiten, in der die Sonne unterschiedliche Sternbilderwege durchläuft und sich damit in einem schiefen Kreis bewegt.[5] In der Perserzeit (539–326 v. Chr.) wurde dann die Einteilung der Ekliptik in die 12 Tierkreiszeichen geschaffen.[6] Diese Entwicklung ist dokumentiert durch hunderte babylonische Keilschrifttafeln, auf denen astronomische Messreihen in babylonischen Zahlzeichen mit Angabe ekliptikbezogener Positionen verzeichnet sind.
Mit dem geozentrischen Weltbild der Philosophie der Antike wurden die am Himmel beobachteten Bewegungen so aufgefasst, dass die im Westen untergehende Sonne bei der nächtlichen Rückkehr nach Osten auf einer sich drehenden Sphäre um die Erde wandert. Diese einer Kugeloberfläche ähnliche Schale mit der Sonne verschiebe sich auch gegen jene der Fixsterne, sodass die Sonne den jeweils 12 Stunden später erscheinenden Sternen gegenübersteht. Mit dieser Vorstellung konnte die aus der Sternbeobachtung schon bekannte Verschiebung des Sternenhimmels in Einklang mit der Beobachtung gebracht werden, dass die Sonne bezüglich der Sterne innerhalb eines Jahres um die Erde zu kreisen scheint, auf der Ekliptik genannten Bahn – nach heutigem Verständnis als geozentrisch bezogene scheinbare Bewegung. Unter Zugrundelegung dieses Weltbildes beschäftigten sich mehrere griechische Philosophen mit der Ekliptik und den darauf befindlichen Tierkreiszeichen. Durch erhaltene Schriften oder Erwähnungen bei späteren Autoren sind insbesondere bekannt Anaximander (6. Jahrhundert v. Chr.), Pythagoras (6. Jahrhundert v. Chr.), Oinopides (5. Jahrhundert v. Chr.) und Eudoxos von Knidos (4. Jahrhundert v. Chr.).[7] Mitte des 2. Jahrhunderts schrieb dann der Gelehrte Claudius Ptolemäus eine umfassende Darstellung des astronomischen Wissens. In diesem Werk, dem Almagest, definiert er die Ekliptik als Großkreis auf der Sphäre und erstellt eine Reihe – auch trigonometrischer – Berechnungen, z. B. eine Tabelle der Schiefe (der Ekliptik).[8]
In Europa wurde eine Einteilung der Ekliptik in zwölf gleich große Sektoren während der Antike eingeführt. In Indien hingegen wurde traditionell die Mondbahn nach Sterngruppen längs der Ekliptik in 27 Nakshatras (Stationen des Monds) aufgeteilt.[9] Diese Anzahl entspricht der abgerundeten Zahl an Tagen eines siderischen Monats (27,32 d), womit der Mond in der Regel jeden Tag in einem anderen Haus aufgeht. Das bereits im Yajurveda (etwa 1000 v. Chr.) überlieferte System ist im asiatischen Raum weit verbreitet; umstritten ist, ob ihm ein von chinesischen Astronomen entwickeltes System vorausging.[10]
Schon in vorislamischer Zeit wurde die Aufteilung in Nakshatras auch im arabischen Raum bekannt, und umgebildet in das Manazil al-Qamar (Mondhäuser) genannte System, das die Ekliptik nach Sterngruppen in 28 Mondhäuser gliedert.[11] Nach der Bildung mächtiger Kalifate entstanden aber Bildungszentren und Bibliotheken, an denen die griechischen astronomischen Texte in die arabische Sprache übersetzt wurde. Insbesondere der Almagest des Claudius Ptolemäus wurde bereits Ende des 8. Jahrhunderts übersetzt und gewann großen Einfluss.[12] Die Werke wurden aber nicht nur rezipiert, sondern auch weiterentwickelt. So wurden etwa die von Ptolemäus übermittelten Werte für die Schiefe der Ekliptik von arabischen Astronomen verbessert (Al-Battani, 9. Jahrhundert).[13]
Das Frühmittelalter bietet eine Reihe astronomischer Texte. Es sind aber weitgehend Exzerpte aus spätantiken Sammelwerken (hauptsächlich Macrobius Ambrosius Theodosius und Martianus Capella).[14] Erst spätere Autoren, wie Georg von Peuerbach und Regiomontanus (beide Mitte 15. Jahrhundert) beschäftigen sich mit der Ekliptik.[15] Schließlich präzisiert Kopernikus in seiner Schrift Commentariolus (Kapitel De motibus, qui circa Solem apparent): Die Achse ist um etwa 23 1/2 Grad schräggestellt. Der Erdmittelpunkt bleibt auf der Ebene der Ekliptik (Übersetzung Hans Günter Zekl, gekürzt; dieser Wert war genau 23° 30′ 00″ im Jahr 1532). Seit etwa der Zeitenwende wissen Astronomen, dass die Erdachse präzediert, allerdings wurde der heute bekannte Wert von 25.700 bis 25.800 Jahren erst im 13. Jahrhundert festgestellt, und der Wert der Präzessionskonstante wurde von Friedrich Wilhelm Bessel anhand der Messungen von Sternörtern durch James Bradley aus der Mitte des 18. Jahrhunderts präzise bestimmt. Dass sich außer ihrer Richtung auch die Schiefe der Ekliptik verändert, ahnte man erst im Mittelalter. Man vermutete damals, dass ihr Winkel im Lauf der Jahrtausende alle Werte von 0° bis 90° annimmt. Erst im 16. Jahrhundert wurde klar, dass die Schwankungsbreite viel geringer ist; Kopernikus ging von Änderungen der Ekliptikschiefe zwischen max. 23° 52′ und min. 23° 28′ aus, nur rund 24′.[16]
Schwankung der Erdachse und der Ekliptikschiefe
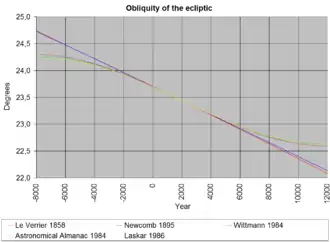
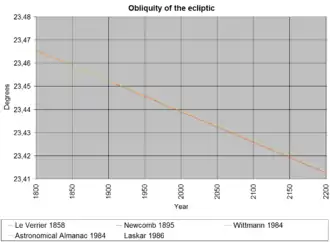
Auch der Winkel der Ekliptikschiefe ändert sich langperiodisch durch die gegenseitigen Gravitationseinflüsse der Körper im Sonnensystem. Daher variiert ε innerhalb von etwa 41.000 Jahren zwischen etwa 21° 55′ und 24° 18′. Dieser Effekt trägt neben den Schwankungen der Exzentrizität der Erdbahn (100.000 Jahre) und der Präzession (25.780 Jahre) zur Entstehung der Eiszeiten bei (als einer der Faktoren der langfristig-regelmäßigen, natürlich auftretenden Klimaschwankungen, die man Milanković-Zyklen nennt):
Als erste Näherung wird für die mittlere Ekliptikschiefe angegeben:
- ε0 = 23° 26′ 21,45″ − 46,8″·T,
wobei T den Zahlenwert der Zeit in Julianischen Jahrhunderten seit der Epoche J2000.0 (1. Januar 2000 12.00 TT) bezeichnet
(in der Epoche J2000.0 hat die Ekliptik die Richtung (0, sin(ε), cos(ε))).[17]
Im Jahr 2014 beträgt die Schiefe der Ekliptik also:
- 23° 26′ 14,9″ = 23,43747°.
Überlagert wird der Wert der mittleren Ekliptikschiefe von der Wirkung der Nutation in einer Größenordnung von Δε = ±9,21″ (Nutation in Schiefe).
Tabelle der Ekliptikschiefe
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Man sieht bereits aus diesen 6 von 40 Jahrtausenden, dass sich die Änderung per 500 Jahre von −2,9′ auf −3,9′ beschleunigt, weil die absinkende Sinuswelle noch bis ins 5. Jahrtausend steiler wird (Mittelwert ε = 23° 06′ um das Jahr 4300).
Messung der Schiefe der Ekliptik
Die klassische Methode, die Ekliptikschiefe zu bestimmen, ist die präzise Messung der Mittagshöhen der Sonne (z. B. mit dem Meridiankreis) und deren Wiederholung zu verschiedenen Jahreszeiten. Aus dem Höhenwinkel erhält man durch Berücksichtigung von geografischer Breite, atmosphärischer Strahlenbrechung (Refraktion) und verschiedener Eichgrößen des Fernrohrs die Deklination δ der Sonne.
Durch den zeitlichen Verlauf der Deklination δ zwischen den Grenzen +ε und −ε erhält man ε zum mittleren Zeitpunkt der Beobachtungen. Dabei wird δ als sinusähnliche Funktion von ε und der Länge λ angesetzt.
Von Leonhard Euler bis Laplace
Die Ursache für die Änderungen der Ekliptikschiefe sind die anderen 7 Planeten, deren Bahnebenen von jener der Erde um 1° (Jupiter, Uranus) bis 7° (Merkur) abweichen. Sie üben Drehmomente auf die Erde aus wegen deren Abplattung (Abweichung von der Kugelform 0,3353 %, Durchmesser am Äquator etwa 43 km größer als zwischen den Polen).
Die erste theoretische Berechnung dieser Änderung der Ekliptikschiefe ε gelang Leonhard Euler im Jahr 1754. Als Ergebnis seiner Analyse erhielt er für die Änderungsrate dε/dt der Ekliptikschiefe den Wert −47,5″/Jh., woraus er für das Jahr 1817 für die Schiefe den Wert ε = 23° 27′ 47,0″ prognostizierte. Als die Massen der Planeten genauer bekannt waren, wiederholte Joseph-Louis Lagrange 1774 Eulers Berechnungen, woraus er −56,2″ pro Jahrhundert und für 1817 den Wert 23° 47′ 48,0″ erhielt. 1782 kam er mit verbesserter Theorie auf −61,6″/Jh., wogegen Jérôme Lalande um 1790 in seinen Astronomietafeln die Änderungsrate −33,3″/Jh. und für 1817 den Wert 23° 47′ 38,9″ erhielt.
Diese doch beträchtlichen Unterschiede zwischen so hervorragenden Mathematikern veranlassten Pierre-Simon Laplace (1749–1827) zu einer noch gründlicheren Analyse, aus der ein Schwankungsbereich von ±1,358° folgte. Er weicht vom heutigen Wert nur um 0,6° (in 20 Jahrtausenden) ab. Der Mannheimer Astronom Friedrich Nicolai – ein Schüler von Carl Friedrich Gauß – errechnete für das Jahr 1800 die Änderungsrate dε/dt = −49,40″/Jh. Auch andere berühmte Himmelsmechaniker erforschten den Verlauf dieser fundamentalen Größe, und Urbain Le Verrier publizierte 1858 die theoretische Formel
wobei die Zeit in julianischen Jahrhunderten ab 1850.0 zählt. Le Verrier bemerkte aber als erstes, dass sein Wert von −47,6″/Jh. dem beobachteten Wert von etwa −46,8″/Jh. leicht widersprach.
Von Newcomb (1895) bis zur Raumfahrt
Gegen Ende des 19. Jahrhunderts war der allgemein akzeptierte Wert jener von John Nelson Stockwell (1873), nämlich ±1,311379° bzw. −48,968″/Jh. Später wurde für dieses Problem ein Preis ausgeschrieben, für den Paul Harzer 1895 alle säkularen Bahnstörungen der acht Planeten berechnete. Um hierfür die (vor Albert Einstein noch unerklärliche) Periheldrehung des Merkur zu berücksichtigen, nahm er eine spezielle Massenverteilung in der Sonne an, und erhielt 47,499″ (bzw. ohne die Korrektur 0,14″ weniger). Im selben Jahr entwickelte Simon Newcomb seine Theorie der Fundamentalastronomie und benutzte Beobachtungen vieler berühmter Sternwarten. Seine bis etwa 1970 verwendeten Werte sind:
- ( die Zeit in julianischen Jahrhunderten ab 1900.0).
Eine Neuberechnung von Eric Doolittle 1905 wich davon nur um 0,07″ ab, was nicht viel über der damaligen Messgenauigkeit von ε lag. Das in T quadratische Polynom ist allerdings nur als Approximation zu verstehen, da sich die Ekliptikschiefe periodisch ändert. Um 1960 nahm man eine Periode von 41.050 Jahren an.
Aktueller Stand der Theorie
Heute sind die Planetenmassen durch interplanetare Raumsonden etwa 100-mal genauer bekannt – und daher auch die langfristigen Änderungen der Ekliptikschiefe. Im Jahr 1970 berechnete J. Lieske deren säkularen Trend zu:
Aus allen geeigneten Beobachtungen bis zurück zur Zeit Leonhard Eulers (s. oben) erhält man für 1817 den Wert ε = 23° 27′ 47,1″ – was von den Werten der damaligen Astronomen nur um 0,5″ abweicht.
1984 ging man auf die Bezugs-Epoche J2000.0 über:
Der Unterschied zum System 1970 liegt mit 0,008″ unter der damaligen Standardabweichung.
Axel D. Wittmann publizierte 1984 eine Ausgleichsrechnung, die auf circa 60 von 230 historischen Solstitialbeobachtungen fußt, welche von ihm neu reduziert wurden. Er erhielt neben einem Polynom 3. Grades auch eine Formel mit einem Sinusglied:[18]
( die Zeit in julianischen Jahrhunderten seit J2000.0)
Der Astronomical Almanac führte 1984 folgende Formel ein, die auch von der IAU angenommen wurde:[19]
- dezimal
-
- ( die Zeit in julianischen Jahrhunderten seit J2000.0)
Jacques Laskar gibt 1986 eine Formel an, die im Zeitraum J2000.0 ± 10.000 Julianische Jahre Gültigkeit hat.[20] Die größte Abweichung beträgt zwischen den Jahren +1000 und +3000 etwa 0,01″ und an den Gültigkeitsgrenzen einige wenige Bogensekunden:
- wobei den Zahlenwert der Zeit in julianischen Jahrzehntausenden seit J2000.0 bezeichnet.
Literatur
- Andreas Guthmann: Einführung in die Himmelsmechanik und Ephemeridenrechnung. BI-Wiss.-Verl., Mannheim 1994, ISBN 3-411-17051-4.
- John David North: Viewegs Geschichte der Astronomie und Kosmologie. Braunschweig/Wiesbaden 1997.
- B. L. van der Waerden: Erwachsende Wissenschaft. Basel/Boston/Stuttgart 1980.
Weblinks
- Kurzer Einführungsartikel (Memento vom 4. Mai 2012 im Internet Archive)
- Astronomical Constants (USNO Circular 163) (PDF-Datei; 3,3 MB)
- Obliquity of the Ecliptic for any Given Date and Time
Einzelnachweise
- John David North: Viewegs Geschichte der Astronomie und Kosmologie, 1 Vorgeschichte
- John M. Steele: Observation and Predictions of Eclipse Times by Early Astronomers, Dordrecht/Boston/London 2000, S. 176
- Alfred Forke: The World-Conception of the Chinese, New York 1975, p. 1998
- John David North: Viewegs Geschichte der Astronomie und Kosmologie, 2 Antikes Ägypten, S. 8–11
- B. L. van der Waerden: Erwachsende Wissenschaft, S. 78
- B. L. van der Waerden: Erwachsende Wissenschaft, S. 124
- B. L. van der Waerden: Erwachsende Wissenschaft, S. 258–261
- Übersetzung Karl Manitius, Erstes Buch, Sechzehntes Kapitel
- George Thibaut: Astronomie, Astrologie und Mathematik in Grundriss der indo-arischen Philologie und Altertumskunde, Straßburg 1899, S. 12
- George Thibaut: Astronomie, Astrologie und Mathematik, S. 13
- Daniel Martin Varisco: Medieval Agriculture and Islamic Science, Seattle/London 1994
- John David North: Viewegs Geschichte der Astronomie und Kosmologie, 8 Der östliche Islam, S. 122–126
- John David North: Viewegs Geschichte der Astronomie und Kosmologie, 8 Der östliche Islam, S. 126–128
- Hans Günter Zekl: Nicolaus Kopernikus: Das neue Weltbild, Hamburg 1990, S. XLVIII
- Ernst Zinner: Entstehung und Ausbreitung der Copernicanischen Lehre, München 1988, Peuerbach, Regiomontan
- Nicolaus Copernicus: De revolutionibus, 1543, 2. Buch, 2. Kapitel bzw. 3. Buch, 10. Kapitel.
- Andreas Guthmann: Einführung in die Himmelsmechanik und Ephemeridenrechnung. 1994, S. 160.
- Axel D. Wittmann: On the Variation of the Obliquity of the Ecliptic, in: Mitteilungen der Astronomischen Gesellschaft, Vol. 62, S. 201–204.
- Astronomical Almanac for the year 1984, Washington, D.C., 1983. S. S26
- J. Laskar: New Formulas for the Precession, Valid Over 10000 years, Astronomy and Astrophysics, 157 (1986), 68