Exzentrizität (Astronomie)

Die Exzentrizität ist in der Astronomie eine charakteristische Größe für die Bahn eines Himmelskörpers; sie ist eines seiner Bahnelemente. Sie wird in der Regel als eine auf ein anderes Bahnelement bezogene Größe, also als numerische Exzentrizität gebraucht. Zum Beispiel bei einer elliptischen Bahn ist sie auf deren große Halbachse bezogen.

Rot: Elliptische Keplerbahn mit (numerischer) Exzentrizität 0,7
Grün: Parabolische Keplerbahn mit Exzentrizität 1
Blau: hyperbolische Keplerbahn mit Exzentrizität 1,3

Man spricht deshalb in der Astronomie in der Regel nicht von „numerischer Exzentrizität“, sondern nur von „Exzentrizität“ und verwendet dafür das Formelzeichen $e$ . Da letzteres in der Mathematik für die lineare Exzentrizität gebraucht wird (für die numerische Exzentrizität dort $\varepsilon$ ), besteht Verwechslungsgefahr.

Mögliche Werte

Die Exzentrizität, eine dimensionslose Zahl, kann folgende Werte annehmen:

0 für exakt kreisförmige Bahnen,
zwischen 0 und 1 für elliptische Bahnen (wobei Werte nahe 0 kreisähnliche Bahnen auszeichnen, und die Ellipse umso langgestreckter erscheint, je näher die Exzentrizität bei 1 liegt),
1 für exakt parabolische Bahnen,
größer als 1 für hyperbolische Bahnen (je größer der Wert, desto offener die Hyperbel).

Während Werte unter 1 geschlossene Bahnen (also Umlaufbahnen) beschreiben, bezeichnen Werte ab 1 offene Bahnen, die so nur einmalig durchlaufen werden.

Zusammenhang mit anderen Bahneigenschaften

Für eine Umlaufbahn in Form einer Ellipse gilt:

Periapsisdistanz = große Halbachse mal (1 − Exzentrizität): $r_{\mathrm {min} }=a(1-e)$
Apoapsisdistanz = große Halbachse mal (1 + Exzentrizität): $r_{\mathrm {max} }=a(1+e)$
$e={\frac {r_{\mathrm {max} }-r_{\mathrm {min} }}{r_{\mathrm {max} }+r_{\mathrm {min} }}}$

Exzentrizitätswinkel

Exzentrizitätswinkel α
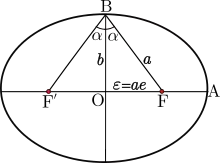
Formelzeichen ε und e sind vertauscht (entspricht Gebrauch in Mathematik)

Der Exzentrizitätswinkel α ist ein aus der Exzentrizität e abgeleitetes Bahnelement:

\alpha =\arcsin(e)

Er ist der vom Nebenscheitel (B) aus gesehene Winkel zwischen Brennpunkt (F) und Mittelpunkt (O) (siehe nebenstehende Abbildung).

Exzentrizitäten einiger Umlaufbahnen

Unter den Bahnen der Planeten im Sonnensystem hat die Bahn der Venus mit 0,0068 die geringste Exzentrizität (ist also am kreisähnlichsten) und die Bahn des Merkurs mit 0,2056 die größte. Die Exzentrizität der Erdbahn beträgt 0,0167. Die Werte für die anderen Planetenbahnen können in der Liste der Planeten des Sonnensystems nachgelesen werden.

Deutlich größere Exzentrizität weisen die Bahnen einiger transneptunischer Objekte auf: Pluto mit 0,2502, Eris mit 0,4383 und Sedna mit 0,8587, es gibt dort aber auch Objekte mit niedriger Exzentrizität wie (486958) Arrokoth mit 0,051.

Kometenbahnen haben generell sehr unterschiedliche Werte der Exzentrizität. Bei (kurz-)periodischen Kometen liegt die Exzentrizität meist zwischen 0,2 und 0,7,[1] wobei es unter ihnen einige gibt, die sehr hoch exzentrische elliptische Bahnen haben, beispielsweise hat der Komet Halley die Exzentrizität 0,967. Bei fast allen nicht- oder lang-periodischen Kometen mit einer Umlaufzeit von mehr als 200 Jahren liegt der Wert nur knapp unter 1, so hat der Komet 153P/Ikeya-Zhang bei einer Umlaufzeit von rund 366 Jahren eine Bahnexzentrizität von 0,990.

Der Asteroid 1I/ʻOumuamua stammt aus dem interstellaren Raum und bewegt sich auf einer Hyperbelbahn durch das Sonnensystem. Seine Exzentrizität von 1,1995 ist also deutlich größer als 1.[2] Der Komet C/1980 E1 (Bowell) stammt aus dem Sonnensystem, wurde aber durch einen nahen Vorbeiflug an Jupiter auf eine hyperbolische Bahn mit einer Exzentrizität von 1,0577 abgelenkt und wird das Sonnensystem verlassen.[3][4] Der im August 2019 entdeckte Komet 2I/Borisov hat eine deutlich höhere Exzentrizität von etwa 3,4 und ist das zweite im Sonnensystem entdeckte interstellare Objekt.[5]

Siehe auch

Einzelnachweise

John S. Lewis: Physics and Chemistry of the Solar System. Academic Press, San Diego CA u. a. 1995, ISBN 0-12-446740-7 (englisch, online [abgerufen am 29. März 2015]).
'Oumuamua (A/2017 U1). In: JPL Small-Body Database Browser. Abgerufen am 2. Dezember 2017 (englisch).
Michael F. Ahearn, D. G.Schleicher, R. L.Millis, P. D.Feldman, D. T. Thompson: Comet Bowell 1980b. In: Astronomical Journal. Nr. 89, 1984, S. 579–591, doi:10.1086/113552, bibcode:1984AJ.....89..579A.
JPL Small-Body Database Browser: C/1980 E1 (Bowell)
MPEC 2019-S72 : 2I/Borisov = C/2019 Q4 (Borisov). In: Minor Planet Center. 24. September 2019, abgerufen am 24. September 2019 (englisch).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Kometen-1] John S. Lewis: Physics and Chemistry of the Solar System. Academic Press, San Diego CA u. a. 1995, ISBN 0-12-446740-7 (englisch, online [abgerufen am 29. März 2015]).

[2] 'Oumuamua (A/2017 U1). In: JPL Small-Body Database Browser. Abgerufen am 2. Dezember 2017 (englisch).

[Ahearn1984-3] Michael F. Ahearn, D. G.Schleicher, R. L.Millis, P. D.Feldman, D. T. Thompson: Comet Bowell 1980b. In: Astronomical Journal. Nr. 89, 1984, S. 579–591, doi:10.1086/113552, bibcode:1984AJ.....89..579A.

[jpl_bowell1980b-4] JPL Small-Body Database Browser: C/1980 E1 (Bowell)

[:0-5] MPEC 2019-S72 : 2I/Borisov = C/2019 Q4 (Borisov). In: Minor Planet Center. 24. September 2019, abgerufen am 24. September 2019 (englisch).