Rute (Einheit)
Die Rute (regional auch Gerte[1]) ist sowohl eine alte Längenmaßeinheit als auch ein traditionelles Messgerät der Längenmessung. Im deutschsprachigen Raum wurde die Rute üblicherweise mit dem Zeichen ° abgekürzt.[2]
.jpg.webp)
(da die preußische Rute ein Zwölf-Fuß-Maß darstellte, entsprach die halbe Rute de facto einem Klafter)
Verschiedene Länder und Berufszweige benutzten als Rute fast 20 unterschiedliche Längenmaße zwischen 3 und 9 Meter, überwiegend aber von 3,6 bis 5 Meter oder 1½ bis 3 Klafter. Sie waren (mit zwei Ausnahmen) ganzzahlige Vielfache der allgemein verbreiteten Einheit Fuß (ca. 30 cm).
Überblick
In eindeutigem Kontext wurde der Begriff der Rute oft auch synonym zur Quadratrute bzw. Geviertrute, also zum entsprechenden Flächenmaß verwendet. Im Zusammenhang mit der Hufe gab es auch eine so genannte Flächenrute. Sie entsprach der Fläche einer Rutenbreite der Hufe. Bei der mit der sächsischen Königsrute gemessenen Hufe waren das 1 Rute × 270 Ruten, also 270 sächsische Königquadratruten oder ein Zwölftel der gesamten Landhufe, also knapp zwei Hektar.[3]
Das Längenmaß Rute wurde mit unterschiedlichen Definitionen auf der ganzen Welt verwendet. Ihre Länge übertraf dabei aber stets eineinhalb Klafter einerseits und sie maß andererseits auch nie mehr als fünf Klafter. Jedoch wurden in der Praxis fast überall Maßruten zwischen etwa drei und fünf Meter verwendet. Es kann zwischen gewöhnlichen und speziellen Feldmesserruten unterschieden werden. Die speziellen wurden von den alten Landvermessern bevorzugt, da nur sie es erlaubten, die Länge der Diagonale eines zu vermessenden Quadrats mit sehr großer Präzision in einem rationalen und ganzzahligen Wert auszudrücken und damit die Kalkulation mit der unhandlichen, da irrationalen Quadratwurzel aus Zwei vermied. Das Rutenmaß kam vor allem in der Landesvermessung sowie im Hoch- und Tiefbau zur Anwendung. Noch länger in Gebrauch war die Rute als rod in den angloamerikanischen Ländern, wo sie auch pole oder perch genannt wird.
Angloamerikanisches Maßsystem
- Die englische Rute (rod) misst 5½ Yard, gleich 16½ Fuß oder 198 Zoll. Somit beträgt die Länge der englischen Rute genau (16½ × 0,3048 =) 5,0292 Meter.
- Die Breite des metrologischen Referenzackers Oxgang wurde zu 40 Ruten definiert. Diese Breite, Furlong, also Pflugfurchenlänge genannt, wird in zehn Vermessungsketten geteilt. Jede Kette, englisch Chain, enthält vier Ruten, also 66 Fuß. Die gesamte Ackerbreite beträgt somit 660 englische Fuß. Die englische Meile enthält damit genau acht Ackerbreiten und somit auch genau 320 englische Ruten.
Die Rod wird heute kaum mehr gebraucht; an ihre Stelle ist der Foot getreten.
Typische Ruten
Abhängig zu ihrem jeweiligen Verhältnis zum Fußmaß kann zwischen etwa eineinhalb Dutzend verschiedenen Ruten-Typen unterschieden werden. Wobei die Feldmesser Ruten über drei oder vier Klafter – wie etwa die 30 Fuß langen Königsruten – aufgrund ihrer unhandlichen Länge in der Praxis fast immer nur als Halbruten verwendeten. Außerdem war es durchaus üblich, dass in ein und demselben Maßsystem zwei oder drei verschiedene Rutentypen parallel zueinander benutzt wurden. Beispielsweise konnte es sein, dass die größeren Entfernungsmaße, zum Beispiel die Meile, ein Vielfaches der zweiglatten 16-Fuß-Rute waren, hingegen die Landvermesser eine siebenglatte 14-Fuß-Rute verwendeten und die Bauhandwerker schließlich zu ihrer dreiglatten Zwölf-Fuß-Rute griffen.
| Name (des Ruten-Typus) | Fuß | Glätte | Länge zu 0,3 m |
Anmerkungen | |
|---|---|---|---|---|---|
| 5-Klafter- = Königsrute | 30 | 5 | 9,00 m | Die Königshufe wurde, theoretisch, in Königsruten zu dreißig Fuß vermessen. | |
| Doppelte Feld-Rute | 28 | 7 | 8,40 m |
| |
| Viereinhalb-Klafter-Rute | 27 | 3 | 8,10 m | ||
| Fünf-Doppelschritt-Rute | 25 | 5 | 7,50 m | ||
| Vier-Klafter-Rute | 24 | 3 | 7,20 m | ||
| Arpenteur-Rute | 22 | 11 | 6,60 m | Die elfglatte Arpenteur-Rute war in Frankreich die Rute der Feldvermesser. | |
| Dreieinhalb-Klafter-Rute | 21 | 7 | 6,30 m | Diese eineinhalb Feldruten messendes Maß war nur sehr vereinzelt anzutreffen. | |
| Gromatici-Doppelrute | 20 | 5 | 6,00 m | Manchmal wurde die Rute auch als 20-Fuß-Maß definiert. Siehe: Oldenburg, alt. | |
| Drei-Klafter-Rute | 18 | 3 | 5,40 m | In Frankreich war sie auch als „Königsrute“ bekannt. Es gab sie auch anderswo. | |
| Surveyor-Rute | 16½ | 11 | 4,95 m | Die praktische 16½-Fuß-Rute ist die meist verwendete elfglatte Vermessungsrute. | |
| Waldrute | 16 | 2 | 4,80 m | Aus vierfacher Fuß-Verdopplung entstand ein beliebtes Längenmaß: die Waldrute. | |
| „Wiesenrute“ | 15 | 5 | 4,50 m | Diese 1½-Gromanici-Rute ist die Hälfte der 30-Fuß-Königsrute aus der Königshufe. | |
| Feldrute | 14 | 7 | 4,20 m | Die siebenglatte 14-Fuß-Rute wurde von Feldmessern im Allgemeinen bevorzugt. | |
| Fünf-Schritt-Rute | 12½ | 5 | 3,75 m | Die fünfglatte 2½-Doppelschritt-Rute galt zum Beispiel auch in Frankfurt am Main. | |
| Bau- oder Werkrute | 12 | 3 | 3,60 m | Die dreiglatte Zwölf-Fuß Bau- oder Werkrute wird auch als „kleine Rute“ bezeichnet. | |
| Arpenteur-Halbrute | 11 | 11 | 3,30 m | Da die Arpenteur-Rute sehr lang war, war das Messinstrument oft auch ihre Hälfte. | |
| Gromatici-Rute | 10 | 5 | 3,00 m | Die römische Zwei-Doppelschritt-Rute wurde auch anderswo verwendet. |
Die weit verbreitetsten Rutentypen waren die mittleren, zwischen vierzehn und sechzehneinhalb Fuß liegenden. Die Bauhandwerker ihrerseits bevorzugten zumeist die etwas kürzere Zwölf-Fuß-Rute.
Gewöhnliche Ruten
Als gewöhnliche Ruten werden diejenigen Ruten bezeichnet, deren Verhältnis zum Fußmaß die arithmetische Glätte fünf nicht übertrifft, also zwei-, drei- oder höchstens fünfglatt sind. Diese gewöhnlichen Ruten eigneten sich hervorragend zur reinen Längenmessung. So maß die alte römische Rute (pertica) zwei Doppelschritt, gleich zehn römische Fuß und war also fünfglatt. Die dreiglatte Zwölf-Fuß-Rute hingegen misst zwei Klafter und hieß zumeist Bau- oder Werkrute. Die zweiglatte 16-Fuß-Rute wurde im deutschen Sprachgebiet im Allgemeinen als Waldrute bezeichnet. Sie wurde später innerhalb des Heiligen Römischen Reiches zur gesetzlichen Standard-Rute, während dies zuvor meist die zweieinhalb Klafter lange 15-Fuß-Rute war. Zuweilen waren auch 18-Fuß-Ruten zu drei Klaftern anzutreffen, seltener 20- oder 21-Fuß-Ruten oder noch längere Ruten.
- Die römische Pertica war die Zehn-Fuß-Rute der Gromatici. Sie entsprach eben zwei römischen Doppelschritt, also etwas mehr als 2,96 Meter.
- Die preußische Rute war eine Zwölf-Fuß-Rute. Sie entsprach gemäß der offiziellen Umrechnung genau 1669,56 Pariser Linien, also etwa knapp 3,77 m.[4]
- Die kulmische Rute war bis 1816 das Maß im Osten Preußens. 1 kulmische Rute entsprach 4,3892 m, 1 kulmischer Fuß 26,261 cm und eine Meile 7900,500 m.
- Die polnische Rute war eine 15-Fuß-Rute. Das zugrunde liegende Maß ist der alte Kulmer Fuß, der bei etwa 127,7 Pariser Linien, ca. 288,1 mm liegt. Die polnische Rute misst daher etwa 4,32 m.[5]
- Die fränkische Rute war eine 16-Fuß-Rute, wobei der Nürnberger Fuß fünfundzwanzig vierundzwanzigstel bairische Fuß beträgt. Empirisch lag der Wert der Großen Fränkischen Rute bei gut 4,86 m.[6]
All diese gewöhnlichen Ruten wurden von den alten Landvermessern gemieden, da sie es nicht erlaubten, die äußerst praktische rationale Triangulation des Quadrats zu bewerkstelligen. Um diese zu ermöglichen, griffen sie zu ihren eigenen, sieben- oder elfglatten Ruten.
Die mit der Besteuerung von Landbesitz betrauten Beamten verstanden aber nicht immer, weshalb die Feldmesser partout mit ihren speziellen Ruten messen wollten. Obwohl sehr viele Fälle bekannt sind, in denen die offiziellen Flächenmaße der Besteuerung identisch waren mit dem speziellen Rutenmaß der Vermesser, kam es in anderen Fällen auch zu einem Doppelstandard aus gewöhnlichen und speziellen Rutenmaßen. Die Vermesser benutzten für ihre eigentliche Arbeit im Felde ihre speziellen, sieben- oder elfglatten Vermessungsruten. Sie rechneten aber gegebenenfalls, ganz zum Schluss ihrer Vermessungsarbeit, die Endergebnisse in Flächenwerte zu gewöhnlichen Quadratruten um. Oder aber, um sich diese Umrechnung zu ersparen, teilten sie die 15- oder 16-Fuß-Ruten einfach durch vierzehn. Sie hatten dadurch einen ein bzw. zwei Vierzehntel längeren, zunächst inoffiziellen Arbeitsfuß erhalten. Nicht selten wurde dieser neue Vermessungsfuß später dann der offizielle und/oder wurde von benachbarten Ländern übernommen. Genau hieraus erklärt sich auch die allgegenwärtige Präsenz der Ratio 15:14 oder 16:14 zwischen verschiedenen Fußmaßen.
Spezielle Ruten der Landvermesser
Als spezielle Feldruten sind diejenigen Ruten zu bezeichnen, deren Ratio zum Fuß sieben- oder elfglatt ist. Seit der frühen Antike wurden sie in der Feldvermessung bevorzugt angewendet. Bis weit in die unsere Neuzeit hinein war die traditionelle Landvermessung ohne sie in der Praxis gar nicht möglich oder zumindest erheblich erschwert. Erst seit der allgemeinen Verbreitung von Rechenschiebern Ende des 18. Jahrhunderts waren die speziellen Feldruten nicht mehr unentbehrlich.
Die siebenglatte Feldrute
Die 14-Fuß-Rute ist die Feldrute par excellence. Sie erfreute sich weiter Verbreitung und großer Beliebtheit. Zur oben genannten Fränkischen Waldrute zu 16 Fuß gab es auch eine Fränkische Feldrute zu 14 Fuß. Diese wurde zum Beispiel auch in Meiningen mit dem empirischen Wert von 4255,622 mm[7] verwendet.
Die elfglatten Arpenteur- oder Surveyor-Ruten
Drei Feldruten (sowie auch zum Beispiel das spanische Vermesser-Seil) sind elfglatt:
- Die einfache Elf-Fuß-Rute war vor allem als die Halbrute der französischen Arpenteur-Rute praktiziert. Dieser Ruten-Typus war aber zuweilen auch anderswo anzutreffen.
- Die wichtige 16½-Fuß-Rute, als das eineinhalbfache der gerade genannten halben Arpenteur-Rute, war in der Praxis sicherlich die beste elfglatte Rute. Elfglatt ist sie zweifelsohne, da in der Definition der Glätte problemlos auch negative ganzzahlige Potenzen zugelassen werden können: 2−1 × 31 × 50 × 70 × 111 = 16½. Dieser Messstab mittlerer Länge ist sehr gut handhabbar. Er ist weder zu kurz, noch zu lang. Die Surveyor-Rute ist somit der französischen 22-Fuß-Definition überlegen. Gelegentlich finden sich Vermesserruten vom Typ der englischen Surveyor-Ruten auch im Heiligen Römischen Reich. Zumeist wurden hier aber die siebenglatten 14-Fuß-Ruten bevorzugt. Das Resultat ist das gleiche, da die rationale Triangulation des Quadrates sowohl mit siebenglatten, als auch mit elfglatten Vermesserruten möglich ist.
- Die ganze 22-Fuß-Rute war die offizielle Vermesserrute der französischen Arpenteure. Die französischen Vermesser rechneten zwar in der offiziellen Einheit, arbeiteten aber in der Praxis nicht selten nur mit der halben Messlatte, da die ganze, mit über sieben Meter Länge, eher unhandlich war.
Das spanische 24 ¾ Fuß messende Seil war ein weiteres, elfglattes Messgerät. Dieses offizielle spanische, Cuerda genannte Maß war zu neunundneunzig Viertel des spanischen Fußes definiert.[8] In manchen regionalen Maßsystemen waren auch vereinzelt andere Maße als die Rute, so zum Beispiel die Vermessungskette, sieben- oder elfglatt.
Vermessungsruten geringerer Glätte als elf
Dreizehn-, siebzehn- oder neunzehnglatte Ruten wurden von den Vermessern nicht verwendet. Dies erklärt sich daraus, dass es einfach keinen Sinn ergibt, die Berechnungen durch die willkürliche Einführung eines neuen, hohen Primfaktors künstlich und zugleich nutzlos zu erschweren. In seltenen Fällen kann man auf Ratios schlechterer Glätte als elf stoßen. Diese erweisen sich aber, fast immer, als künstlich angepasst. So wurde die Sächsische Feldmesserrute neuzeitlich zu genau 182 (neue) Sächsische Zoll definiert. 182 (2×7×13) ist aber eine 13-glatte Zahl. Ein Faktor, der in der traditionellen Metrologie absolut nie verwendet wurde. In Wirklichkeit war jene eine 15-Fuß-Rute zum gleichen Fußmaß, wie dem der Hamburger Geestrute oder auch dem Stuttgarter Fußmaß. In allen drei Fällen handelt es sich um das Maß des alten liudolfingischen Königsfußes. (Königsruten der Fränkischen Hufen).
Eine große Ausnahme ist aber die niederländische Rute, die tatsächlich dreizehn niederländische Fuß misst. Der niederländische Fuß wird bemerkenswerterweise in nur elf Zoll geteilt. Zwölf niederländische Zoll ist die Länge des kyrenaischen Fußes, der seinerseits 25:24 zum römischen Fuß steht. Der niederländische Fuß ist also der sogenannte kyrenaische Handelsfuß. Die niederländischen Metrologen hielten es nun für opportun, eine Rute zu dreizehn dieser Fuß zu wählen, da sie erkannt hatten, dass zehn solcher Ruten annähernd genau 132 spanische Fuß einerseits und 128 kölnische Fuß andererseits beinhalten. Der bei dieser Gleichsetzung auftretende theoretische Fehler beträgt nur (213×35 ÷ 55×72×13 =) 0,0016 Prozent. Selbstverständlich war in den spanischen Niederlanden der spanische Fuß ein wichtiges Referenzmaß. Natürlich war aber, in Holland, ebenfalls der kölnische Fuß sehr wichtig, da dieser ja der rheinische Handelsfuß ist, zum eigentlichen rheinischen Fuß also in der Ratio 11:12 steht. Aus diesen Gründen hielten es die niederländischen Metrologen für akzeptabel, die Primzahl 13 in ihr Maßsystem aufzunehmen. Die Primfaktoren sieben und elf hingegen erleichterten die Berechnungen der traditionellen Feldvermessung erheblich. Daher rührt die Verbreitung dieser speziellen Feldruten.
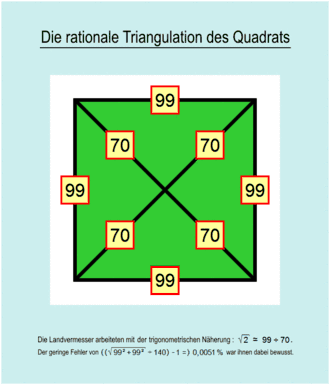
Die rationale Triangulation des Quadrats
Der Zahlenwert von Wurzel Zwei ist irrational, für eine Triangulation benötigt man einen passenden Näherungswert als rationalen Zahlenwert. Seit dem frühen Altertum versuchten die Mathematiker und Landvermesser, den Längenwert der Diagonale eines Quadrats so auszudrücken. Sie näherten sich dabei dem irrationalen Zahlenwert von Wurzel Zwei in ganz und gar vergleichbarer Weise, genau so, wie wir es heute auch noch tun, wenn wir Wurzel Zwei als gerundeten Wert in einem Dezimalbruch angeben: 1 + (4142/10.000) oder 1 + (414 213 562/1000000000).
Schon im ersten Drittel des zweiten Jahrtausends (−1700 ± 100) v. Chr. kannten die Babylonier den guten Näherungs-Sexagesimal-Wert 1 + 24×60−1 + 51×60−2 + 10×60−3 = 30547÷21600 = 1,41421296. (Cf. das Tontäfelchen YBC 7289) Da √2 − (30547 ÷ 21600) ≈ 1.41421356 − 1.41421296 = 0.000000599, kannten die alten Babylonier den Wert von Wurzel Zwei auf fünf volle, korrekte Dezimalstellen hinter dem Komma genau bei einem Fehler von rund einem halben Millionstel.
Die Babylonier maßen also der Diagonalen ihrer Nippur-Elle genau 42,42638 Fingerbreit zu, wie es eine andere auf diesem Tontäfelchen vermerkte Sexagesimalzahl angibt, (vs. real ungefähr 42,426407 Fingerbreit). In Millimeter und ausgehend vom siebenglatten Wert misst diese Diagonale nach dem babylonischen Näherungswert genau (518,616 × (30547 ÷ 21600) =) 733,43347 mm, gegenüber etwa 733,4337808637 mm in Wirklichkeit. Anders ausgedrückt : Vor fast viertausend Jahren hatten die alten Babylonier die Diagonale ihrer Quadratelle nur um weniger als 310,864 Nanometer unterbewertet.
Der Präzisionsanspruch der Landvermesser ergibt sich aus ihrer Praxis. Wobei die gute Glätte für die Bequemlichkeit der Berechnungen stets wichtiger war, als das Bedürfnis nach allzu großer, absoluter Genauigkeit. Die obige Zahl 30547, Faktor des exzellenten babylonischen Näherungswertes ist elfmal die Primzahl 2777. Die Näherung ist also 2777-glatt, was leider eine sehr schlechte Glätte ist, ja schlimmer, eine nur scheußlich zu nennende. Sehr früh wurden deshalb verschiedene Wurzel-Zwei-Näherungswerte von den Geometern untersucht, wobei die möglichst gute Glätte im Vordergrund stand. (Vgl. französisch Méthodes d’approximation de racine carrée de deux.)

| Fraktion | faktorielle Glätte |
relative Abweichung |
Tatsächliche Verwendung des betreffenden Näherungswertes | gerundete Ratio (Präzision) |
|---|---|---|---|---|
| 3 ÷ 2 | dreiglatt | + 6,0660 % | Nie verwendet, da auf indiskutable Weise viel zu ungenau. Nicht praxistauglich. | 3600 |
| 7 ÷ 5 | siebenglatt | – 1,0051 % | Im Alten Ägypten Anfang des 3. Jahrtausends v. Chr., vgl. das sogenannte Konstruktions-Remen. | 600 |
| 17 ÷ 12 | siebzehnglatt | – 0,1735 % | Nicht verwendet. Relativ hoher Primfaktor und gleichzeitig weit ungenauer als 99:70. | 100 |
| 99 ÷ 70 | elfglatt | + 0,0051 % | Sehr gute Näherung; im Vermessungswesen seit der Antike omnipräsent. | 3 |
Andere, sogar genauere Näherungen waren bekannt, wie sich die Theonfolge der nebenstehenden Tabelle ergibt: etwa der Wert 239 ÷ 169 oder 577 ÷ 408. Jedoch beinhalten diese hohe Primfaktoren. Die recht genaue Approximation 99 ÷ 70 eignet sich zur Landvermessung sehr gut. Beispiel : Vorausgesetzt die Katheten eines rechtwinkligen gleichschenkligen Dreiecks messen jeweils genau 99 Zentimeter, so überschreitet der Hypotenusenwert die Länge von 140 cm um nur etwa 71,437 µm, also zirka ein Vierzehntel eines Millimeters.
Als der griechische Mathematiker Theon von Smyrna die verschiedenen Wurzel-Zwei-Näherungswerte systematisch untersuchte und darüber eine theoretische Abhandlung schrieb, wurde die mehr als zufrieden stellende elfglatte Näherung 99 ÷ 70 sicherlich schon seit Jahrhunderten, vielleicht schon seit Jahrtausenden von den Landvermessern in der Praxis verwendet. Die 14-Fuß-Feldrute, die zum Beispiel die deutschen Geodäten – nicht nur im Mittelalter, sondern bis weit in unsere Neuzeit hinein – vornehmlich verwendeten, wurden zu ebendiesem Zweck geschaffen. Das Gleiche gilt für die englische Vermessungsrute zu 16 ½ Fuß, sowie für die französische zu 22 Fuß. Siebenglatte Ruten (hier ein weiteres Beispiel einer 14-Fuß-Rute) und die elfglatten Feldmesser-Ruten (hier die beiden bekanntesten) beinhalten stets den internen Faktor sieben bzw. elf:
- Die Kasseler Katasterrute, eine 14-Fuß Feldrute zu vierzehn kölnischen Fuß, also empirisch 3,988760 Meter.[9]
- Die englische Surveyor-Rute, zu (2 × 99 =) 198 englische Zoll, also 5½ Yard gleich 16½ Fuß oder 5,0292 Meter.
- Die französische Arpenteur-Rute, zu 22 Königsfuß, also (22 × 9000 ÷ 27,706 mm) ungefähr 7,1465 Meter.
Die jeweiligen Faktoren sieben bzw. elf, die in der Definition selbst dieser Feldruten enthalten sind, waren dafür ausschlaggebend, dass die rationale Triangulation des Quadrats mit ihrer Näherung √2 ≈ 99 ÷ 70 möglich war. Beachte, dass selbst die etwa 5000 Jahre alte ägyptische Königselle, die ihrerseits direkt auf die Nippurelle zurückgeht – dieses Mal in ihrer Digitus-Definition – den Faktor sieben beinhaltet (1 Elle = 28 Digiti), was diesbezüglich für die altägyptischen Geometer bei ihren jährlich neuen Landvermessungen nach der Nilschwemme natürlich äußerst praktisch war.
Die Anwendung des rationalen Näherungswertes war folgendermaßen:
Die Feldmesser bestimmten zum Beispiel ein quadratisches Feld mit 140 Fuß Seitenlänge. Danach wussten sie sofort und ohne weitere Rechnung, dass dessen Diagonale 2×99 = 198 Fuß betrug. Im Falle der elfglatten Rute war es genau umgekehrt. Ein quadratisches Feld zu 12 × 16 ½ = 198 Fuß Seitenlänge, hat die Diagonallänge von 280 Fuß. Nicht allein zur Bestimmung der Länge der Diagonale wurde dieser Näherungswert verwendet. Alle in den Berechnungen vorkommenden Wurzel-Zwei-Faktoren konnten durch 99:70 ersetzt werden. So entstand zum Beispiel die Sächsische Königsrute aus der Fränkischen Königshufe (bzw. der Fränkischen Königsrute). Um, bei einem anderen Hufenzuschnitt, das gleiche Flächenmaß aufrechtzuerhalten, musste die Sächsische Königsrute genau der Quadratwurzel aus 8÷9 multipliziert mit dem Wert der Fränkischen Königsrute entsprechen. Dies lässt sich auflösen in (2√2):3. Ersetzt man √2 durch 99÷70, so erhält man die einfache Ratio von 33:35. Dieses Verhältnis besteht daher zwischen dem alten Sächsischen Königsfuß, der in der Sächsischen Feldmesserrute erhalten blieb, und dem Fränkischen Fuß, der in der Stadt Nürnberg bewahrt wurde.
Beispiel eines diagonal abgeleiteten Maßsystems:
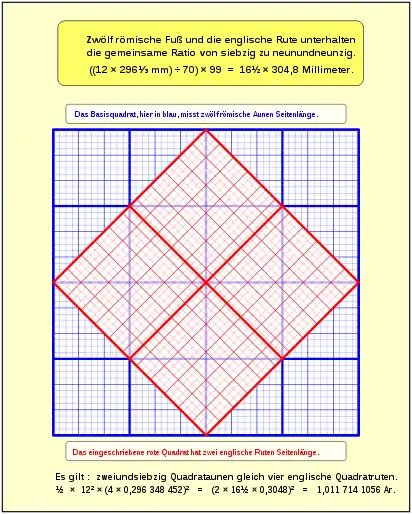
Die rationale Triangulation des Quadrats stand bei der Entstehung vieler Maßsysteme Pate. So sind die englischen Längen- und Flächenmaße eine direkte, diagonale Ableitung der römischen Maße. Das englische metrologische Referenzfeld war der so genannte Oxgang, der 40 × 60 englische Surveyor-Ruten misst. Wobei 40 Ruten gleich ein Furlong, also eine Pflugfurchenlänge ist. Die Fläche des Oxgangs, der englischen Kleinhufe, beträgt fünfzehn englische Acker (acres), zugleich aber auch zwölf römische Erbteile (heredia). Die beiden Fußmaße stehen im Verhältnis 36:35.
In vereinfachter Form, zeigt die Illustration das Verhältnis der englischen Surveyor-Rute zur spätrömischen 4-Fuß-Aune. Das englische Maßsystem ist über die rationale Triangulation des Quadrats direkt vom römischen Maßsystem abgeleitet. Die englische Feldrute misst daher: ((12 × 296⅓ mm) ÷ 70) × 99 = 16½ × 304,8 Millimeter = 5,0292 Meter. Nicht wenige gleichartige Verhältnisse sind bekannt, auch zwischen dem englischen und dem alten rheinischen Fuß.
Regionale bzw. nationale Rutenmaße und ihre jeweiligen Werte
Die folgende Liste ist, zumindest bezüglich der bis ins 19. Jahrhundert aufrechterhaltenen Rutenmaße des Heiligen Römischen Reiches, weitgehend erschöpfend. Sie enthält außerdem einige wichtige Rutenmaße benachbarter Staaten wie Frankreich, Polen, Schweiz, Holland oder Belgien, sowie England. In dieser Liste fehlen weiterhin noch die italienischen Rutenmaße, sowie die des Baltikums und anderer ost- und südosteuropäischen Staaten. Da die meisten Rutenmaße im Verlauf der Geschichte und je nach Region zugleich als 12-, 14-, 15- und 16-Fußruten existierten, bevor sie später innerhalb des Heiligen Römischen Reiches zumeist als gesetzliche 16-Fuß-Ruten normalisiert wurden, fügt diese Liste, soweit nicht eh schon vorhanden, den Rutentypus in den Namen der Rute ein. Allerdings wurden bereits vorhandene, alte Namen wie Geest-, Marsch- oder Katasterrute beibehalten.
| Residenzstadt |
Land oder Region Anmerkung |
Name des Rutenmaßes |
Fuß Ratio |
Fuß in mm |
Rute in mm |
Rute2 in m² |
Ref. |
Glätte |
|---|---|---|---|---|---|---|---|---|
| Paris | Königreich Frankreich | Franz. Arpenteur-Rute | 22 | 324,839 | 7146,467 | 51,0720 | (1) | 11 |
| Oldenburg | Grafschaft Oldenburg | Alte Oldenburger Rute | 20 | 295,879 | 5917,580 | 35,0178 | (2) | 5 |
| Paris | Königreich Frankreich | Französische Königsrute | 18 | 324,839 | 5847,110 | 34,1887 | (3) | 3 |
| Bremen | Freie Hansestadt | Große Bremer Rute | 20 | 289,350 | 5787,000 | 33,4894 | (4) | 5 |
| Antwerpen | Herzogtum Brabant | Große Antwerpener Rute | 20 | 286,800 | 5736,000 | 32,9017 | (5) | 5 |
| Altenburg | Sachsen-Gotha-Altenburg | Große Altenburger Rute | 20 | 283,794 | 5675,880 | 32,2156 | (6) | 5 |
| Brüssel | Königreich Belgien | Große Belgische Rute | 20 | 275,750 | 5515,000 | 30,4152 | (7) | 5 |
| Oldenburg | Herzogtum Oldenburg | Neue Oldenburger Rute | 18 | 295,879 | 5325,822 | 28,3644 | (8) | 3 |
| London | Vereinigtes Königreich | Englische Surveyor-Rute | 16½ | 304,797 | 5029,155 | 25,2924 | (9) | 11 |
| Neustrelitz | Mecklenburg-Strelitz | Preußische Waldrute | 16 | 313,854 | 5021,656 | 25,2170 | (10) | 2 |
| Wiesbaden | Herzogtum Nassau | Metrische „Feldrute“ (1853) | 10 | 500,000 | 5000,000 | 25,0000 | (11) | 5 |
| Nürnberg | Freie Reichsstadt | Fränkische Waldrute | 16 | 303,973 | 4863,568 | 23,6543 | (12) | 2 |
| Prag | Königreich Böhmen | Böhmische Waldrute | 16 | 297,560 | 4760,960 | 22,6667 | (13) | 2 |
| Stockholm | Königreich Schweden | Schwedische Waldrute | 16 | 296,906 | 4750,496 | 22,5672 | (14) | 2 |
| Neuenburg | Fürstentum Neuenburg | Neuenburger Weinbergrute | 16 | 293,258 | 4692,128 | 22,0161 | (15) | 2 |
| Hannover | Kurfürstentum Hannover | Calenberger Waldrute | 16 | 292,095 | 4673,515 | 21,8417 | (16) | 2 |
| Arolsen | Waldeck-Pyrmont | Arolsener Waldrute | 16 | 291,365 | 4661,840 | 21,7328 | (17) | 2 |
| Schwerin | Mecklenburg | Mecklenburger Waldrute | 16 | 291,000 | 4656,000 | 21,6783 | (18) | 2 |
| Karlsruhe | Baden-Durlach | Alte Karlsruher Waldrute | 16 | 291,000 | 4656,000 | 21,6783 | (19) | 2 |
| Bückeburg | Schaumburg-Lippe | Bückeburger Waldrute | 16 | 290,100 | 4641,600 | 21,5445 | (20) | 2 |
| Detmold | Lippe-Detmold | Detmolder Waldrute | 16 | 289,513 | 4632,208 | 21,4574 | (21) | 2 |
| Bremen | Freie Hansestadt | Bremer Waldrute | 16 | 289,350 | 4629,600 | 21,4332 | (22) | 2 |
| Schwerin | Mecklenburg-Schwerin | Rostocker Waldrute | 16 | 287,699 | 4603,191 | 21,1894 | (23) | 2 |
| Gotha | Sachsen-Gotha | Gothaer Waldrute | 16 | 287,618 | 4601,888 | 21,1774 | (24) | 2 |
| Köln | Historisches Rheinland | Kölnische Waldrute | 16 | 287,393 | 4598,280 | 21,1442 | (25) | 2 |
| Neuenburg | Fürstentum Neuenburg | Neuenburger Waldrute | 16 | 287,150 | 4594,400 | 21,1085 | (26) | 2 |
| Hamburg | Freie Hansestadt | Hamburger Geestrute | 16 | 286,572 | 4585,144 | 21,0235 | (27) | 2 |
| Gera | Reuß jüngerer Linie | Geraer Waldrute | 16 | 286,197 | 4579,152 | 20,9686 | (28) | 2 |
| Braunschweig | Braunschweig-Wolfenbüttel | Braunschweiger Waldrute | 16 | 285,362 | 4565,798 | 20,8465 | (29) | 2 |
| Dresden | Kurfürstentum Sachsen | Dresdner Straßenrute | 16 | 283,190 | 4531,042 | 20,5303 | (30) | 2 |
| Greiz | Reuß älterer Linie | Kursächsische Waldrute | 16 | 283,190 | 4531,040 | 20,5303 | (31) | 2 |
| Rudolstadt | Schwarzburg-Rudolstadt | Rudolstädter Waldrute | 16 | 282,200 | 4515,200 | 20,3870 | (32) | 2 |
| Weimar | Sachsen-Weimar-Eisenach | Weimarer Waldrute | 16 | 281,980 | 4511,680 | 20,3553 | (33) | 2 |
| Frankfurt am Main | Freie Reichsstadt | Frankfurter Waldrute | 16 | 281,923 | 4510,760 | 20,3470 | (34) | 2 |
| Hildesheim | Hochstift Hildesheim | Hildesheimer Waldrute | 16 | 280,175 | 4482,800 | 20,0955 | (35) | 2 |
| Warschau | Königreich Polen | Polnische Wiesenrute | 15 | 288,000 | 4320,000 | 18,6624 | (36) | 2 |
| Danzig | Freie Hansestadt | Danziger Wiesenrute | 15 | 286,885 | 4303,278 | 18,5182 | (37) | 3 |
| Dresden | Kurfürstentum Sachsen | Sächsische Feldmesserrute | 15 | 286,337 | 4295,050 | 18,4475 | (38) | 5 |
| Leipzig | Markgrafschaft Meißen | Leipziger Wiesenrute | 15 | 285,639 | 4284,583 | 18,3577 | (39) | 3 |
| Meiningen | Sachsen-Meiningen | Fränkische Feldrute | 14 | 303,973 | 4255,622 | 18,1103 | (40) | 7 |
| Gotha | Sachsen-Gotha | Gothaer Feldrute | 14 | 287,618 | 4026,652 | 16,2139 | (41) | 7 |
| Hamburg | Freie Hansestadt | Hamburger Marschrute | 14 | 286,572 | 4012,001 | 16,0962 | (42) | 7 |
| Kassel | Hessen-Kassel | Kasseler Katasterrute | 14 | 284,911 | 3988,760 | 15,9102 | (43) | 7 |
| Erfurt | Fürstentum Erfurt | Erfurter Feldrute | 14 | 283,260 | 3965,640 | 15,7263 | (44) | 7 |
| Sondershausen | Schwarzburg-Sondershausen | Sondershausener Feldrute | 14 | 282,500 | 3955,000 | 15,6420 | (45) | 7 |
| Wien | Erzherzogtum Österreich | Österreichische Werkrute | 12 | 316,081 | 3792,968 | 14,3866 | (46) | 3 |
| Berlin | Königreich Preußen | Preußische Werkrute | 12 | 313,854 | 3766,242 | 14,1846 | (47) | 3 |
| Amsterdam | Spanische Niederlande | Niederländische Rute | 13 | 283,133 | 3680,734 | 13,5478 | (48) | 13 |
| Nürnberg | Freie Reichsstadt | Fränkische Werkrute | 12 | 303,973 | 3647,676 | 13,3055 | (49) | 3 |
| Hanau | Kurfürstentum Hessen | Hanauer Werkrute | 12 | 297,458 | 3569,500 | 12,7413 | (50) | 3 |
| Frankfurt am Main | Freie Reichsstadt | Römische Werkrute | 12½ | 284,610 | 3557,630 | 12,6567 | (51) | 5 |
| Emden | Kurfürstentum Hannover | Calenberger Werkrute | 12 | 292,095 | 3505,136 | 12,2860 | (52) | 3 |
| Fulda | Hochstift Fulda | Fuldaer Werkrute | 12 | 282,880 | 3394,560 | 11,5230 | (53) | 3 |
| Madrid | Königreich Spanien | Spanische Werkrute | 12 | 278,635 | 3343,620 | 11,1798 | (54) | 3 |
| Christiania | Dänemark-Norwegen | Dänisch-Norwegische Rode | 10 | 313,763 | 3137,632 | 9,8447 | (55) | 5 |
| Karlsruhe | Großherzogtum Baden | Neue Badische Rute (1810) | 10 | 300,000 | 3000,000 | 9,0000 | (56) | 5 |
| Oldenburg | Herzogtum Oldenburg | Oldenburger Katasterrute | 10 | 295,879 | 2958,790 | 8,7544 | (57) | 5 |
| Bern | Kanton Bern | Alte, kleine Berner Rute | 10 | 293,258 | 2932,580 | 8,6000 | (58) | 5 |
| München | Kurfürstentum Bayern | Kleine Bayrische Rute | 10 | 291,722 | 2917,215 | 8,5101 | (59) | 5 |
| München | Königreich Bayern | Kleine Bayrische Rute | 10 | 291,859 | 2918,592 | 8,5182 | [10] | 5 |
| Stuttgart | Württemberg, Hohenzollern | Kleine Schwäbische Rute | 10 | 286,490 | 2864,903 | 8,2077 | (60) | 5 |
| Wiesbaden | Herzogtum Nassau | Metrische „Werkrute“ (1853) | 10 | 250,000 | 2500,000 | 6,2500 | (61) | 5 |
Anmerkung: Bis auf eine Ausnahme enthält diese Tabelle keine Ruten mit exakt gleichen Werten, da es sich in solchen Fällen nur um die Übernahme eines bestehenden Maßes handelt. Beispiel: Im Herzogtum Schleswig galt eine 16-Fuß-Rute, die identisch war mit der Hamburger Geestrute.[11] Umgekehrt enthält diese Liste aber – sehr wohl – viele Fälle, in denen es sich eigentlich um das gleiche Maß handelt, das aber lokal mit nur leicht abweichenden Werten aufbewahrt wurde. Abweichungen von unter ± 0,05 % gelten in der alten Metrologie noch als tadellos, zwischen ± 0,05 % und ± 0,10 % nur als mittelmäßig und bis zu ± 0,15 %, bestenfalls als sehr schlecht.
- Im Alten Testament ist ebenfalls von Ruten die Rede. Eine Rute entsprach sechs Großen Ellen, wobei aber historisch, zu verschiedenen Zeiten, verschiedene Ellen verwendet wurden.
Siehe auch
Literatur
- Otto Brandt: Urkundliches über Maß und Gewicht in Sachsen. Sächsisches Ministerium des Innern, Dresden 1933.
- Fritz Verdenhalven: Alte Meß- und Währungssysteme aus dem deutschen Sprachgebiet. Was Familien- und Lokalgeschichtsforscher suchen. 2. wesentlich vermehrte und völlig überarbeitete Auflage. Degener, Neustadt an der Aisch 1993, ISBN 3-7686-1036-5.
- Johannes Langer: Heimatkundliche Streifzüge durch Fluren und Orte des Erzgebirges und seines Vorlandes. Schwarzenberg/Sachsen 1931
Einzelnachweise
- Christine Demel u. a.: Leinach. Geschichte – Sagen – Gegenwart. Gemeinde Leinach, Leinach 1999, S. 648 (1 Gerte = 12 Schuh = 3,51 m).
- W.E.A. v. Schlieben, J.V Montag: Vollständiges Hand- und Lehrbuch der gesamten niederen Meßkunde. 3. Auflage. Verlag der Ernst'schen Buchandlung, Quedlinburg und Leipzig 1845, S. 9.
- Heinrich Walter: Königshufen, Waldhufen und Sächsische Acker. (Memento des Originals vom 16. März 2012 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis. (PDF; 444 kB) In: Neues Archiv für Sächsische Geschichte, N° 51, 1930, S. 4, Mitte.
- Angelo Martini: Manuale di metrologia. Edition Loescher, Turin 1883, S. 74.
- Angelo Martini: Manuale di metrologia. Edition Loescher, Turin 1883, S. 180.
- Angelo Martini: Manuale di metrologia. Edition Loescher, Turin 1883, S. 414.
- Angelo Martini: Manuale di metrologia. Edition Loescher, Turin 1883, S. 342.
- Angelo Martini: Manuale di metrologia. Edition Loescher, Turin 1883, S. 321.
- Angelo Martini: Manuale di metrologia. Edition Loescher, Turin 1883, S. 148.
- Zeitschrift des Kœniglich Bayerischen Statistische Bureau, Erster Jahrgang 1869, S. 140: "Amtliche Zusammenstellung der Verhältnisszahlen für die Umrechnung der im diessrheinischen Bayern bisher giltigen Maasse und Gewichte in die durch das Gesetz vom 29. April 1869, die Maas- und Gewichtsordnung betreffend, festgestellten neuen Maasse und Gewichte.
- Angelo Martini: Manuale di metrologia. Edition Loescher, Turin 1883, S. 41.