Mantellinie
Als Mantellinien bezeichnet man in der Darstellenden Geometrie die erzeugenden Geraden verschiedener Flächen:
- Die Mantellinien einer Kegelfläche gehen durch einen festen Punkt (Spitze) und durchlaufen die Punkte einer Kurve (Leitkurve).[1] Vergleiche die Abbildung am Ende der Einleitung.
- Bei einer Zylinderfläche sind die Mantellinien, die die Leitkurve durchlaufen, parallel.
- Auch die Erzeugenden der Tangentenfläche einer Raumkurve, d. h. die Tangenten an die Kurve, werden Mantellinien genannt.[1]

Bei Mantelflächen von Körpern werden insbesondere in der Schulgeometrie die Strecken zwischen Grundfläche und Deckfläche oder Spitze Mantellinien genannt. Diese liegen in den in der Schule betrachteten Spezialfällen auf den Mantelliniengeraden im Sinne der Darstellenden Geometrie.
Darstellende Geometrie
In der Darstellenden Geometrie werden zunächst die Geraden, die eine (zunächst unbeschränkte) Mantelfläche erzeugen, wie in der Einleitung beschrieben, als Mantellinien bezeichnet.[2] Tatsächlich gezeichnet wird dann ein beschränkter Ausschnitt dieser Geraden. Die Mantellinien sind hier wichtig[2]
- zur Konstruktion der Kontur eines kegelartigen Körpers und damit auch zur Bestimmung sichtbarer bzw. verdeckter Teile eines undurchsichtigen Körpers (die Abbildung am Ende der Einleitung deutet verdeckte Teile der Kontur durch gestrichelte Linien an),
- zur Konstruktion des Schattens, den ein solcher Körper bei definierter Beleuchtung wirft.
Elementar- und Schulgeometrie
Hier werden in der Regel nur Strecken auf drei bestimmten Arten von Rotationskörpern als Mantellinien bezeichnet. Diese Rotationskörper sind der gerade Kreiskegel, der rotationssymmetrische Kegelstumpf und der gerade Kreiszylinder.[3] In diesen Fällen sind alle Mantellinien kongruent und daher gleich lang. Häufig wird hier auch deren gemeinsame Länge einfach als „Mantellinie“ bezeichnet, in diesem Artikel wird dagegen immer zwischen den Strecken und deren Länge unterschieden.
Gerader Kreiskegel
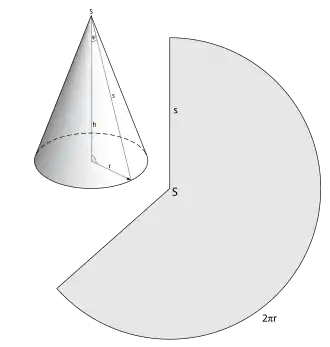
Jede Verbindungsstrecke zwischen einem Punkt des Grundkreises und der Spitze ist eine Mantellinie. Diese sind mit ihren Teilstrecken die einzigen Strecken, die ganz auf der Mantelfläche liegen. Andere Verbindungsstrecken von zwei Punkten des Mantels liegen stets im Inneren des Kegelkörpers.[3] Die Länge s einer Mantellinie ist der Radius des Kreissektors, den der abgewickelte Mantel bildet, vergleiche die Abbildung rechts.
Rotationssymmetrischer Kegelstumpf
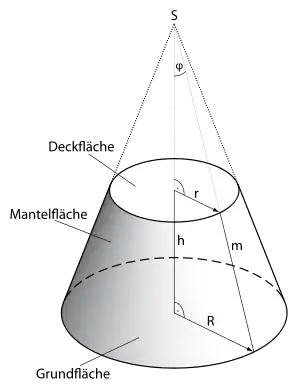
Ein rotationssymmetrischer Kegelstumpf ist der Körper, der aus einem geraden Kreiskegel hervorgeht, wenn man bei diesem Kegel zwischen Grundfläche und Spitze mit einer Schnittebene parallel zur Grundfläche einen Kegel abschneidet. Die Verbindungsgerade der Mittelpunkte von Grund- und Deckfläche ist Symmetrieachse des Kegelstumpfes. Jede Ebene, die diese Achse enthält, schneidet den Mantel in einer Mantellinie und alle Mantellinien liegen auf einer solchen Ebene durch die Achse. Die Mantellinien sind mit ihren Teilstrecken die einzigen Strecken, die ganz auf der Mantelfläche liegen. Andere Verbindungsstrecken von zwei Punkten des Mantels liegen stets im Inneren des Kegelstumpfes.[3]
Gerader Kreiszylinder

Wie beim Kegelstumpf ist die Verbindungsgerade der Mittelpunkte von Grund- und Deckfläche Symmetrieachse des Zylinders. Jede Ebene, die diese Achse enthält, schneidet den Mantel in einer Mantellinie und alle Mantellinien liegen auf einer solchen Ebene durch die Achse. Die Mantellinien sind mit ihren Teilstrecken die einzigen Strecken, die ganz auf der Mantelfläche liegen. Andere Verbindungsstrecken von zwei Punkten des Mantels liegen stets im Inneren des Kreiszylinders.[3]
Die Länge h einer Mantellinie entspricht der Länge der Höhe des Zylinders. Zwei Seiten des abgewickelten Mantels, eines Rechtecks, sind Mantellinien, die anderen zwei Seiten sind die Grund- bzw. Deckkreislinie. Vergleiche die Abbildung rechts.
Weblinks
Der englische Begriff slant height kommt dem Begriff „Mantellinie eines geraden Kreiskegels“ im Sinne einer Streckenlänge nahe, wie er in der Schulmathematik für gerade Kreiskegel gebraucht wird.
- Slant height of a right cone: Englische Erläuterung des englischen Begriffes bei Math Open Reference, mit interaktivem Java-Applet.
Literatur
- Rolf Baumann: Geometrie für die 9./10. Klasse. Zentrische Streckung, Satz des Pythagoras, Kreis- und Körperberechnungen. 4. Auflage. Mentor-Verlag, München 2003, ISBN 3-580-63635-9, S. 95 ff. (Mantellinie in der Schulgeometrie).
- Reinhold Müller: Leitfaden für die Vorlesungen über Darstellende Geometrie. 2. Auflage. Vieweg, Braunschweig 1903, S. 32 f. ([1.Ex..pdf PDF] [abgerufen am 24. Mai 2013]).
- Karl Rohn und Erwin Papperitz: Lehrbuch der Darstellenden Geometrie. 1. Auflage. Salzwasser GmbH, Paderborn 1911, S. 362 ff. (Buch bei Google Books mit Zugriff auf Auszüge [abgerufen am 24. Mai 2013]).
Einzelnachweise
- Müller (1903)
- Rohn (1911)
- Baumann (2003)