Rollen
Das Rollen ist eine Bewegungsart runder Körper – insbesondere von Rädern – bei der die Bewegungsarten Drehung und Verschiebung auf eine bestimmte Weise kombiniert werden. Ein kreisrunder Körper, der sich auf einer ebenen Fläche geradlinig bewegt, rollt genau dann, wenn der Mittelpunkt während einer Umdrehung einen Weg zurücklegt, der seinem Umfang entspricht. Wenn der Weg kleiner ist, dann hat er Schlupf. Bei Rädern spricht man auch vom Durchdrehen, falls der Weg null ist. Wenn der Weg größer ist, dann gleitet der Körper. Dies ist beispielsweise beim Bremsen von Fahrzeugen der Fall, wenn die Räder blockieren. Im Folgenden wird schlupfloses Rollen beschrieben.
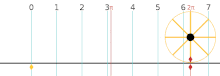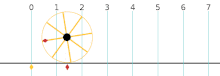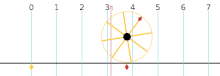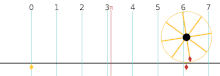

Der Berührpunkt, also der Punkt an dem der Körper den Untergrund berührt, bewegt sich während einer Umdrehung des Körpers entlang eines Weges, dessen Länge dem Umfang des Körpers entspricht. Der Körper muss nicht kreisrund sein, er kann beispielsweise auch elliptisch sein. Die Weglänge wird entlang des zurückgelegten Weges gemessen, also nicht entlang einer geraden Strecke. Der Berührpunkt ist bei schlupflosen Rollbewegungen immer gleichzeitig der Momentanpol. Mathematisch gilt die Rollbedingung, die einen Zusammenhang angibt zwischen dem Winkel (im Bogenmaß) um den sich der Körper in einem bestimmten Zeitraum dreht, dem Radius des Körpers und dem zurückgelegten Weg .
Das Rollen tritt nicht nur bei Rädern auf. Auch die Kugeln in einem Kugellager rollen in den Ringen, die Rollen in Flaschenzügen rollen bezüglich der Seile ebenso wie ein Jo-Jo bezüglich der Schnur. Physikalische Voraussetzung für das Rollen ist Haftreibung zwischen dem rollenden Körper und der Unterlage. Ohne Reibung würde der Körper nur gleiten, ohne sich zu drehen. Die Beschleunigung von rollenden Körpern hängt nicht nur von ihrer Masse ab, wie bei der rein translatorischen Bewegung, sondern auch vom Trägheitsmoment. Zwei Zylinder die auf einer schiefen Ebene herunterrollen, erfahren verschiedene Beschleunigung wenn sie zwar dieselben Massen und äußeren Radien haben, aber unterschiedliche Massenverteilungen haben, beispielsweise bei einem massiven Aluminiumzylinder und einem gleich großen, hohlen Stahlzylinder, siehe eine schiefe Ebene hinabrollendes Rad. Dies ist ein wichtiger Unterschied zum freien Fall, bei dem die Beschleunigung von der Masse unabhängig ist. Sowohl für die geradlinige als auch für die drehende Bewegung muss Arbeit verrichtet werden. Bei rollenden Körpern stehen diese in einem festen Verhältnis zueinander.
Beispiele
Besonders bekannt ist die Rollbewegung bei Fahrzeugrädern, wie sie bei Fahrrädern oder Autos vorkommt. Hier rollen annähernd kreisrunde Körper auf einer meist ebenen Oberfläche. Gleiches gilt auch für auf dem Boden rollende Flaschen oder auf einem Tisch rollende Weingläser, beispielsweise wenn sie umgestoßen werden. Auf einer schiefen Ebene[1] rollen Kugeln oder Zylinder alleine unter der Wirkung der Schwerkraft nach unten. Dies kommt vor allem bei Experimenten vor. Galilei beispielsweise nutzte sie zur Untersuchung der Bewegungsgesetze. Die Bewegung der Rollen in einem Flaschenzug kann als Rollbewegung aufgefasst werden, bei der die Rollen auf dem Seil abrollen. Gleiches gilt für die Bewegung eines Jo-Jos[2] das bezüglich der Schnur an der es hängt, eine Rollbewegung vollführt. Auch in einigen Maschinen kommt sie vor: Die Kugeln in einem Kugellager[3] rollen sowohl auf dem inneren als auch auf dem äußeren Ring ab. Entsprechendes gilt für alle anderen Wälzlager. In einem Planetengetriebe[4] bewegen sich mehrere Zahnräder. Bei einer der möglichen Betriebsarten steht das mittlere Rad – das Sonnenrad – und die anderen Räder – die Planetenräder – rollen um es herum. Auch bei zwei Zahnrädern mit ortsfesten Achsen[5] liegt eine Rollbewegung vor. Man kann sich eines der beiden Zahnräder als feststehend denken, das andere rollt dann auf dem Umfang ab, ähnlich wie beim Planetengetriebe. Bei manchen Verzahnungsarten rollen die einzelnen, sich berührenden, Zähne aufeinander ab, was als Wälzbewegung bezeichnet wird.
Voraussetzungen und Bedingungen
Voraussetzung für die Rollbewegung ist Haftreibung zwischen dem rollenden Körper und dem Untergrund. Wenn keine Reibung vorhanden ist, dann dreht sich der Körper auf der Stelle, falls nur ein Drehmoment auf das Rad wirkt oder er wird ohne Drehung verschoben falls nur eine Kraft auf seinen Schwerpunkt wirkt. Der erste Fall zeigt sich näherungsweise beim Anfahren mit Autos auf spiegelblanker Eisfläche. Die Haftkraft wird hervorgerufen durch eine Kraft die senkrecht zum Untergrund liegt: Die Normalkraft. Bei einer horizontalen Unterlage, entspricht die Normalkraft der Gewichtskraft sofern keine weiteren Kräfte wirken. Bei Sportwagen wird die Anpresskraft durch Spoiler erhöht, was auch die Haftung zwischen Rad und Straße erhöht. An der Berührstelle zwischen dem Körper und dem Untergrund tritt beim Rollen keine Relativbewegung auf, was eine Haftreibung bedingt. Wenn die Antriebskraft bei Fahrzeugen zu groß ist, dann tritt statt der Haftreibung Gleitreibung auf und das Rad dreht durch.[6]
Der Widerstand des gesamten Rades gegenüber der Rollbewegung wird durch die Rollreibung hervorgerufen. Diese entsteht bereits durch minimale Verformungen des Rades aufgrund der Anpresskraft auf den Untergrund und durch Verformung des Untergrundes. Ohne diese Anpresskraft verschwindet zwar die Rollreibung, aber auch die Haftreibung, sodass der Körper nicht mehr rollen kann. Wenn ein Rad das perfekt kreisrund ist, auf eine Oberfläche gedrückt wird, die absolut eben ist, dann entsteht am Berührpunkt theoretisch ein Druck, der jeden realen Körper verformt. Das Phänomen wird als Hertzsche Pressung[7] bezeichnet und ist insbesondere bei steifen Körpern wichtig, die sich nur wenig verformen, wie Eisenbahnräder oder Kugeln eines Kugellagers. Die Reifen von Autos und Fahrrädern sind üblicherweise mit Luft gefüllt und verformen sich stärker, sodass es zu einer ausgeprägten Berührfläche kommt, dem Reifenlatsch. Seine Fläche entspricht bei Autos etwa dem einer Postkarte. Diese Räder rollen dann nicht auf einem Radius der ihrem unverformten Außenradius entspricht. Die Entfernung zwischen Radmittelpunkt und Straßenoberfläche ist der statische Halbmesser (Statischer Radius) des Rades. Ein Punkt auf der Oberfläche der Autoreifens bewegt sich dann zunächst auf einem Radius der dem unverformten Radius entspricht, bis er auf die Straße trifft. Dann verringert sich der Radius allmählich bis auf den statischen Halbmesser. Das Rollen eines Autorades kann jedoch auch modellhaft beschrieben werden mit der Bewegung eines starren Körpers. Für diesen soll gelten, dass er während einer Umdrehung einen Weg zurücklegt der seinem Radius entspricht. Der Radius der unverformten Rades ist zu groß, der statische Halbmesser zu klein. Stattdessen wird der experimentell ermittelte dynamische Halbmesser benutzt.[8]
Kinematik
Die Kinematik ist ein Teil der Mechanik, der sich nur mit den Größen Zeit, Ort, Geschwindigkeit und Beschleunigung befasst. Kräfte, Massen und davon abgeleitete Größen, wie Energie und Leistung bleiben unberücksichtigt.
Das Rollen stellt eine Kombination dar, aus der Drehbewegung (Rotation) und der geraden Bewegung (Translation). Beim Rollen werden beide auf eine bestimmte Art kombiniert: Der rollende Körper legt während einer Umdrehung einen Weg zurück, der seinem Umfang entspricht. Außerdem hat der rollende Körper an den Punkten, an denen er den Untergrund berührt, keine Relativgeschwindigkeit zu ihm. Ein Punkt auf einem Rad setzt zu einem bestimmten Zeitpunkt auf der Straße auf und hebt danach wieder ab, ohne zwischendurch über die Straße zu rutschen oder zu schleifen. Ein Kreisel, dessen Achse senkrecht auf dem Boden steht, rollt also auch dann nicht, wenn er während einer Umdrehung um den Umfang verschoben wird, denn der Berührpunkt hat eine Relativgeschwindigkeit gegenüber dem Boden. Die Drehachse darf nicht senkrecht auf der Unterlage stehen. Außerdem muss es überhaupt eine Berührung geben, zwischen dem rollenden Körper und dem Untergrund. Wenn beispielsweise ein Fahrrad kopfüber auf Lenker und Sattel steht, wie beim Radwechsel üblich, dann rollt das (Hinter- oder Vorder-)Rad auch dann nicht, wenn es während einer Umdrehung einen passenden Weg zurücklegt, beispielsweise durch gleichzeitiges Verschieben des ganzen Fahrrades. Es rollt nicht auf dem Untergrund.
Geeignete Bezugs- und Koordinatensysteme
Die Rollbewegung kann in einem Bezugssystem beschrieben werden, bei dem die Umgebung stillsteht und sich nur der rollende Körper bewegt. Möglich ist es ebenfalls den rollenden Körper als unbewegt anzusehen. Dann bewegt sich aber die gesamte Umgebung. Sinnvoll ist es die Rollbewegung in Gedanken in die zwei Komponenten, Drehung und Verschiebung, aufzuspalten.
- Die Verschiebung des Mittelpunktes des Körpers wird in einem Bezugssystem beschrieben, das gegenüber der Umgebung ruht. Zur Beschreibung ist das allgemein gebräuchliche Koordinatensystem mit x-y-Koordinaten geeignet (Kartesisches Koordinatensystem, im Raum x-y-z-Koordinaten)
- Die Drehung eines beliebigen Punktes um den Mittelpunkt wird in einem Bezugssystem beschrieben, dessen Ursprung zu jedem Zeitpunkt im Mittelpunkt des Körpers liegt. Es bewegt sich also mit dem Körper mit. Zur Beschreibung werden in der Ebene Polarkoordinaten verwendet. (Im Raum Kugel- oder Zylinderkoordinaten)
Rollen in einer Ebene
Die einfachste Form der Rollbewegung ergibt sich, wenn ein Rad mit konstantem Radius, immer aufrecht auf einem ebenen Untergrund steht und sich nur in gerader Linie fortbewegt, beispielsweise beim Geradeausfahren mit einem Fahrrad. Das Rad bewegt sich dann in einer Ebene. Mathematisch kann es als Bewegung in der xy-Ebene beschrieben werden.
Position
Die Position eines Rades, dass auf der x-Achse rollt, kann auf zwei prinzipiell verschiedene Weisen angegeben werden:
- Durch die Angabe der -Koordinate des Mittelpunkts oder des Berührpunkts.
- Durch die Angabe eines Winkels (kleines, griechisches Phi), der die Umdrehungen angibt. In diesem Fall kann der Winkel auch größer als 360° sein. Bei zwei vollen Umdrehungen ist er beispielsweise 2 × 360° = 720°. Er kann auch negativ werden.
Eine der beiden Angaben ist dabei schon ausreichend, denn die andere kann bei bekanntem Radius des Rades berechnet werden. Es gilt die Rollbedingung:
- .
Wenn sich der Mittelpunkt um den Weg weiterbewegt, dann dreht sich auch das Rad um den Winkel weiter. Es gilt:
Ein Körper der innerhalb einer Ebene rollt, hat somit genau einen Freiheitsgrad. Rotation und Translation sind nicht unabhängig voneinander. Dennoch ist es häufig zweckmäßig beide Angaben gleichzeitig zu nutzen.
Geschwindigkeit und Beschleunigung des Mittelpunktes
Die Änderung des Ortes des Mittelpunktes in einem bestimmten Zeitintervall, entspricht der Geschwindigkeit . Die Änderung des Winkels im selben Zeitintervall entspricht der Winkelgeschwindigkeit (kleines, griechisches Omega). Es gilt:
- .
Statt der Winkelgeschwindigkeit kann auch die Drehzahl verwendet werden, die die Anzahl der Umdrehungen in einem Zeitraum angibt. Es gilt:
Die Änderung der Geschwindigkeit des Mittelpunktes in einem bestimmten Zeitintervall, entspricht der Beschleunigung und die Änderung der Winkelgeschwindigkeit im selben Zeitintervall entspricht der Winkelbeschleunigung . Es gilt:
- .
Geschwindigkeit beliebiger Punkte
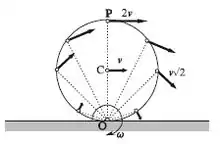
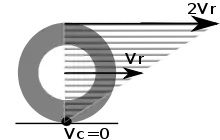
Bei einem rollenden Körper hat jeder Punkt des Körpers eine andere Geschwindigkeit und Beschleunigung bezüglich des Untergrundes. Dies betrifft sowohl den Betrag als auch die Richtung beider Größen. Bei einem Fahrrad bewegt sich beispielsweise der vorderste Punkt des Rades schräg nach unten und der hinterste Punkt bewegt sich schräg nach oben, siehe Bild. Der Betrag ihrer Geschwindigkeiten entspricht aber dem √2-fachen des Mittelpunktes, denn die Diagonale in einem Quadrat hat die √2-fache Länge der Seiten. Der unterste Punkt des Rades, wo es die Straße berührt, hat eine Geschwindigkeit von null bezüglich der Straße, und der oberste Punkt bewegt sich nach vorne mit der doppelten Mittelpunktsgeschwindigkeit.
Der Betrag der Geschwindigkeiten hängt vom Bezugssystem ab: Wenn der Ursprung des Koordinatensystems sich im Mittelpunkt des Rades befindet und sich mit ihm mitbewegt, aber nicht mitrotiert, dann erscheint die Rollbewegung wie eine Reine Drehung um den Ursprung und jeder Punkt auf dem Umfang des Rades hat dieselbe Geschwindigkeit:
Rollen auf einer Ebene
Erfahrungsgemäß kann man mit einem Fahrrad nicht nur in gerader Linie vor und zurückfahren, sondern durch geeignete Lenkmanöver jeden beliebigen Ort einer Ebene erreichen. Die Lage des Berührpunktes wird üblicherweise mit der x- und y-Koordinate in einem kartesischen Koordinatensystem beschrieben. Außerdem müssen noch drei Winkel angegeben werden:[9]
- Ein Winkel, der angibt, wie weit sich der Körper um seine Achse gedreht hat. Bei einem Fahrradreifen kann beispielsweise die Position des Ventils angegeben werden.
- Ein Winkel, der angibt, in welche Richtung die Achse des Körpers zeigt. Bei einem Fahrrad beispielsweise die Stellung des Lenkers.
- Ein Winkel, der die Lage der Achse zum Untergrund angibt. Beim Radfahren in gerader Richtung verläuft diese parallel zum Boden. Bei Kurvenfahrten lehnt sich der Fahrer aber in die Kurve und der Winkel ändert sich.
Siehe auch
- Gyroskopischer Effekt – erklärt, warum rollende Münzen nicht umfallen
- Epizykloide – geometrische Figuren, die durch das Abrollen von Kreisen auf größeren Kreisen entstehen
Einzelnachweise
- Wolfgang Nolting: Grundkurs Theoretische Mechanik 1 – Klassische Mechanik, Springer, 10. Auflage, 2013, S. 307. 332.
- Honerkamp, Römer: Klassische Theoretische Physik, Springer, 4. Auflage, 2012, S. 62.
- Müller-slany: Aufgaben zur Technischen Mechanik, Springer, 2015, S. 250.
- Müller-slany: Aufgaben zur Technischen Mechanik, Springer, 2015, S. 203.
- Gross, Hauger, Wall: Technische Mechanik 3 – Kinetik, Springer, 13. Auflage, S. 282 f.
- Dankert, Dankert: Technische Mechanik, Springer, 7. Auflage, 2013, S. 465, 573 f., 570.
- Dankert, Dankert: Technische Mechanik, Springer, 7. Auflage, 2013, S. 294.
- Breuer, Rohrbach-Kerl: Fahrzeugdynamik, Springer, 2015, S. 7 f.
- Wolfgang Nolting: Grundkurs Theoretische Mechanik 2 – Analytische Mechanik, Springer, 9. Auflage, 2014, S. 12, 47.