Ruck

Ruck ist ein Begriff aus der Kinematik. Er ist die momentane zeitliche Änderungsrate der Beschleunigung eines Körpers. Die SI-Einheit des Rucks ist $\mathrm {m} /\mathrm {s} ^{3}$ . Als Formelzeichen wird üblicherweise $j$ gewählt, in Anlehnung an die englischen Bezeichnungen jerk oder jolt.

Physikalische Größe

Name

Ruck

Formelzeichen

$j$

Größen- und Einheitensystem	Einheit	Dimension
SI	m·s⁻³	L·T⁻³
cgs	cm·s⁻³	L·T⁻³

Formal ist der Ruck die Ableitung der Beschleunigung nach der Zeit, also die zweite zeitliche Ableitung der Geschwindigkeit und die dritte zeitliche Ableitung des Wegs:[1]

j(t)={\dot {a}}(t)={\ddot {v}}(t)={\overset {...}{x}}(t)

wobei $t$ die Zeit, $a$ die Beschleunigung, $v$ die Geschwindigkeit und $x$ der Ort sind.

Wird von einem körperfesten Koordinatensystem ausgegangen, so kann der Ruck für jede Koordinatenrichtung getrennt bestimmt werden, z. B. als Längsruck oder Querruck, oder allgemein vektoriell als Ableitung der Beschleunigung bezüglich dieses Bezugssystems.[2] Insbesondere stellt diese Definition sicher, dass eine gleichförmige Kreisbewegung ruckfrei ist, was dem allgemeinen Sprachgebrauch sowie der Anwendung in der Technik entspricht. Bei Stoßvorgängen ist der Ruck nicht definiert.

Bei der Entwicklung von Aufzugsanlagen und Getrieben werden für den Ruck Werte angestrebt, die im Betrieb Komfort und Sicherheit gewährleisten. Bei Schienenfahrzeugen wird durch die Wahl der Trassierungselemente eine möglichst ruckarme Fahrt beim Übergang in Kurven sichergestellt. Auch bei Achterbahnen wird durch entsprechende Übergänge die Belastung auf den menschlichen Körper reduziert.

Obwohl die physikalische Größe ‚Ruck‘ bei jeder Beschleunigungsänderung definiert ist, wird der Begriff umgangssprachlich in der Regel nur bei kurzen „ruckartigen“ Beschleunigungsänderungen verwendet (siehe Weblinks). Diese treten z. B. beim Anfahren mit einem nicht vorgespannten Abschleppseil auf. „Ruckartig“ bedeutet hier, dass der Gradient des kinematischen Rucks einen hohen Betrag hat.

Beispiel Aufzug

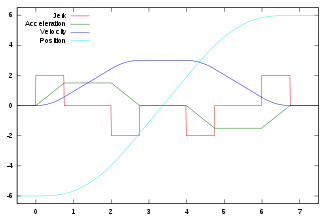
Zusammenspiel zwischen Ruck (rot), Beschleunigung (grün), Geschwindigkeit (blau) und Ort (türkis) über der Zeit. Erläuterung siehe Text.

Das Diagramm zeigt für eine beispielhafte Bewegung eines Aufzugs von der Position −6 zur Position +6 den Zusammenhang zwischen Ruck, Beschleunigung, Geschwindigkeit und Weg (der stückweise lineare Verlauf der Beschleunigung ist typisch für eine Ruckänderung (vierte Ableitung des Weges nach der Zeit) gleich Null):

In der ersten Phase (0–1) ist der Ruck konstant größer Null und die Beschleunigung nimmt damit linear, die Geschwindigkeit quadratisch und der zurückgelegte Weg kubisch zu.
In der zweiten Phase (1–2) ist der Ruck Null, die Beschleunigung ist somit konstant. Die Geschwindigkeit ändert sich linear und der zurückgelegt Weg quadratisch.
In der dritten Phase (2–3) ist der Ruck konstant kleiner Null und die Beschleunigung nimmt linear ab. Die Geschwindigkeit nimmt somit immer langsamer zu.
In der vierten Phase (3–4) sind der Ruck und auch die Beschleunigung Null. Die Geschwindigkeit ist konstant und der zurückgelegte Weg nimmt linear zu.
In der fünften Phase (4–5) ist der Ruck konstant kleiner Null. Die Beschleunigung wird immer negativer, wirkt also als Verzögerung, und die Geschwindigkeit nimmt immer stärker ab.
In der sechsten Phase (5–6) ist der Ruck gleich Null und die Beschleunigung auf einem konstanten negativen Wert. Die Geschwindigkeit nimmt linear ab.
In der siebten Phase (6–7) hat der Ruck wieder einen positiven Wert, die negative Beschleunigung wird zu Null und die Geschwindigkeit geht auf Null zurück. Am Ende der siebten Phase kommt die Bewegung an der Position 6 zum Stillstand.

Der gesamte Zeitablauf wird so gesteuert, dass die Endposition des Aufzugs exakt erreicht wird. Für Beschleunigung und Ruck werden dabei Werte berücksichtigt, die als angenehm und komfortabel empfunden werden.[3]

Das Beispiel wäre vom prinzipiellen Verlauf mit anderen Zahlenwerten auch auf einen fahrenden Zug anwendbar, der über eine Weiche auf ein Parallelgleis fährt. Die dargestellten Größen Ruck, Beschleunigung, Geschwindigkeit und Ort sind dann in Querrichtung zu verstehen.

Die dargestellten Verläufe des Rucks sind aber eher theoretischer Natur. Im Betrieb z. B. bei Seilaufzügen können Schwingungen auftreten, wodurch die Beschleunigungen deutlich größer sind als die Sollwerte.

Ruck bei Fahrzeugen

Bei Fahrzeugen ist der Grund für Rucke häufig ein Lastwechsel (z. B. beim Teillastruckeln). Unterschieden werden:

der Längsruck, die zeitliche Änderung der Längsbeschleunigung
der Querruck, die zeitliche Änderung der Querbeschleunigung.

Anschaulich bedeutet dies, dass der Längsruck bei einem Fahrzeug durch plötzliches Anfahren oder Bremsen verursacht wird, der Querruck dagegen durch plötzliche Änderung des Lenkradwinkels bei einem fahrenden Automobil.

Bei elektronischen Lenksystemen können durch die Zusatzfunktionen auch Querrucke ohne Betätigung des Lenkrads auftreten. Diese müssen aus Sicherheitsgründen auf 5 m/s³ begrenzt sein (ECE R79).

Die Bezeichnungen längs und quer deuten schon an, dass diese Beschleunigungen Komponenten in einem fahrzeugfesten Bezugssystem sind. Ändern sich die Komponenten nicht, so ist der Ruck Null. Bei stationärer Kreisfahrt zeigt der Beschleunigungsvektor immer zum Kreismittelpunkt (Zentripetalkraft), von außen betrachtet ändert er sich also; im fahrzeugfesten Koordinatensystem dagegen bleibt derselbe Beschleunigungsvektor konstant.

Längsruck

Je schneller eine Bremsung eingeleitet oder beendet wird, desto höher ist der Ruck. Eine abrupt eingeleitete Bremsung (Notbremsung) ist mit einem hohen Ruck verbunden. Wenn sich der Insasse nicht schnell genug darauf eingestellt hat und sich nicht abstützt, wird er bei Vorwärtsfahrt nach vorne geworfen (im Auto vom Gurt abgefangen), bei Rückwärtsfahrt in den Sitz gedrückt. Da die Betätigung der Bremse selbst bei einer Notbremsung noch eine gewisse Zeit beansprucht, bleibt der Ruck ein endlicher Wert.

Bleibt die Bremse bis zum Stillstand mit ihrer maximalen Kraft wirksam, so tritt am Ende des Bremsweges ein theoretisch unendlich hoher Ruck auf, weil die Verzögerung (= negative Beschleunigung) plötzlich, also in der Zeitdauer null, endet. Dadurch wird der Insasse durch seine eigene Muskelkraft (Abstützkraft) oder, wenn er sich völlig passiv verhalten hat, durch die vom Gurt ausgeübte Kraft in den Sessel geschleudert und von der Federkraft des Sessels dann zurückgeschleudert. Für diese Bewegungen vergeht allerdings Zeit. Dadurch wird der Ruck endlich, also gemildert. Außerdem entspannen sich elastische Elemente am Fahrzeug (Reifen, Radaufhängung usw.), was ebenfalls wenigstens eine gewisse Zeit dauert.

Im Normalbetrieb löst der routinierte Fahrer die Bremse langsam vor Erreichen des Stillstandes und dehnt damit die Abnahme der Verzögerung zeitlich aus, so dass der Ruck auf ein Minimum herabgesetzt wird.

Fahrzeuge mit Elektroantrieb entwickeln bei einfachen (stufigen) Steuerungskonzepten des Motorstromes einen starken Längsruck bei jeder Beschleunigungsänderung.
Der Fahrkomfort beim Anfahren, Beschleunigen und rekuperativen Bremsen wird durch sanft reagierende Fahrdynamik verbessert, jedoch kann ein sogenannter Warnruck bei autonomen Fahrzeugen genutzt werden, die Aufmerksamkeit zur Überwachung herzustellen.[4]

Querruck

Querruck und Zentripetalbeschleunigung bei einem Fahrzeug, das mit gleichbleibender Geschwindigkeit in eine Kurve fährt. In den unten stehenden Diagrammen ist waagerecht die Zeit oder Bogenlänge, nicht die horizontale Fahrzeugposition aufgetragen.

Der Querruck $k$ als Spezialfall des Rucks ist die Änderung der Zentripetalbeschleunigung $a_{r}$ in Abhängigkeit von der Zeit $t$ :

k={\frac {\mathrm {d} a_{r}(t)}{\mathrm {d} t}}

Die Zentripetalbeschleunigung eines Fahrzeugs ist abhängig von seiner Geschwindigkeit $v$ sowie der Krümmung $\kappa ={\tfrac {1}{r}}$ der Bahn, wobei $r$ der Radius des Krümmungskreises ist:

a_{r}={\frac {v^{2}}{r}}=v^{2}\,\kappa

\Rightarrow k=v^{2}\,{\dot {\kappa }}

für

v=\mathrm {konst.}

Die Krümmung ist bei den verwendeten Trassierungselementen als Funktion der Wegstrecke $s$ gegeben: $\kappa =\kappa (s)$
Mit ${\dot {\kappa }}={\frac {\mathrm {d} \kappa }{\mathrm {d} t}}={\frac {\mathrm {d} s}{\mathrm {d} t}}\cdot {\frac {\mathrm {d} \kappa (s)}{\mathrm {d} s}}=v\cdot {\frac {\mathrm {d} \kappa (s)}{\mathrm {d} s}}$ ergibt sich für den Querruck somit:

k=v^{3}\,{\frac {\mathrm {d} \kappa (s)}{\mathrm {d} s}}.

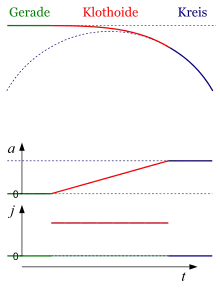
Ein Querruck tritt also beispielsweise auf, wenn sich der Radius einer Kreisbewegung ändert. Wenn in einer Trasse, z. B. einem Bahngleis, ein Kreisbogen unmittelbar auf eine Gerade folgt, so ändert sich an dieser Stelle die Zentripetalbeschleunigung bei schienengebundenen Fahrzeugen sprungartig. Das heißt, die Zeit für diese Änderung ist fast null, und der Querruck wird extrem groß. Verwendet man als Verbindungselement zwischen Gerade und Kreisbogen eine Klothoide, so ändert sich die Zentripetalbeschleunigung linear während der Zeit, die zum Durchfahren der Klothoide benötigt wird. Daher wird der Querruck entsprechend geringer.

In Abschnitten, in denen das Fahrzeug sich auf einer Geraden oder mit konstanter Geschwindigkeit auf einer Kreisbahn bewegt, ändert sich die Zentripetalbeschleunigung nicht. Der Querruck ist somit null.

Bei der Planung von Trassen ist je nach der Bemessungsgeschwindigkeit und dem Fahrkomfort, den man für eine Strecke erreichen will, darauf zu achten, dass der Querruck einen Grenzwert von 0,4 bis 0,6 m/s³[5] nicht übersteigt. Im Extremfall, etwa bei Hochgeschwindigkeitszügen, kann durch Verwendung anderer Übergangsbögen als der Klothoide erreicht werden, dass der Querruck am Anfang des Übergangsbogens nicht sprunghaft, sondern allmählich einsetzt.[6]

Der Querruck bei Lenkmanövern von Straßenfahrzeugen ist wegen der erforderlichen Lenkraddrehung generell begrenzt. Der sanfte Verlauf des Querruckes beim autonomen Fahren ist Forschungsgegenstand, um die Vorhersehbarkeit und den Komfort eines Lenkmanövers zu verbessern, der Ruck würde aufgrund rein mathematischer Algorithmen ansonsten plötzlich und überraschend einsetzen.[7]

Ruckänderung

Die Ruckänderung s (engl. jounce, snap), manchmal Knall genannt, ist ein Begriff aus der analytischen Modellierung der Fahrdynamik von Schienenfahrzeugen und die erste Ableitung des Rucks nach der Zeit:

s(t)={\frac {dj}{dt}}

wobei $t$ die Zeit und $j$ der Ruck ist. Die SI-Einheit der Ruckänderung ist dementsprechend ${\frac {\mathrm {m} }{\mathrm {s} ^{4}}}$ .

Die Ruckänderung spielt in diesen Modellen vor allem eine theoretische Rolle, in dem zumindest bei einem stückweise stetigen Differenzieren oder Integrieren die Ruckänderung jeweils als gleich Null vorausgesetzt wird und auf diese Weise eine Lösung der zugehörigen Gleichungssysteme möglich wird.[8]

Siehe auch

Ruckdämpfer

Einzelnachweise

Bruno Assmann, Peter Selke: Technische Mechanik. 3. Kinematik und Kinetik. OldenbourgWissenschaftsverlag, 2004, ISBN 3-486-27294-2, S. 30.
Beispiel Achterbahn
Drewer, Sebastian: Entwicklung von Hilfsmitteln für die Planung und den Variantenvergleich von Beförderungssystemen in Gebäuden am Beispiel von Aufzügen. KIT Scientific Publishing, 2016, ISBN 978-3-7315-0490-0.: (eingeschränkte Vorschau in der Google-Buchsuche)
Alexander Lange et al.: Automatisiertes Fahren - So komfortabel wie möglich, so dynamisch wie nötig, VDI/VW Gemeinschaftstagung Fahrerassistenz und Integrierte Sicherheit 2014, Wolfsburg, Oktober 2014, abgerufen am 13. Feb. 2022
Ágnes Lindenbach: Straßen und Eisenbahnwesen Vorlesung 4. Archiviert vom Original am 8. Mai 2014; abgerufen am 7. Mai 2014.
Konrad Zilch (Hrsg.): Raumordnung und Städtebau, Öffentliches Baurecht/Verkehrssysteme und Verkehrsanlagen. Springer, 2013, ISBN 978-3-642-41875-4, S. 2152 (eingeschränkte Vorschau in der Google-Buchsuche).
https://mediatum.ub.tum.de/doc/1366901/1366901.pdf Alexander Tobias Lange: Gestaltung der Fahrdynamik beim Fahrstreifenwechselmanöver als Rückmeldung für den Fahrer beim automatisierten Fahren, Dissertation an der TUM 2017, abgerufen am 13. Feb. 2022
Dietrich Wende: Fahrdynamik. Transpress VEB Verlag für Verkehrswesen, Berlin 1983, S. 15.

Weblinks

Wiktionary: Ruck – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Duden

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Bruno Assmann, Peter Selke: Technische Mechanik. 3. Kinematik und Kinetik. OldenbourgWissenschaftsverlag, 2004, ISBN 3-486-27294-2, S. 30.

[2] Beispiel Achterbahn

[3] Drewer, Sebastian: Entwicklung von Hilfsmitteln für die Planung und den Variantenvergleich von Beförderungssystemen in Gebäuden am Beispiel von Aufzügen. KIT Scientific Publishing, 2016, ISBN 978-3-7315-0490-0.: (eingeschränkte Vorschau in der Google-Buchsuche)

[4] Alexander Lange et al.: Automatisiertes Fahren - So komfortabel wie möglich, so dynamisch wie nötig, VDI/VW Gemeinschaftstagung Fahrerassistenz und Integrierte Sicherheit 2014, Wolfsburg, Oktober 2014, abgerufen am 13. Feb. 2022

[5] Ágnes Lindenbach: Straßen und Eisenbahnwesen Vorlesung 4. Archiviert vom Original am 8. Mai 2014; abgerufen am 7. Mai 2014.

[6] Konrad Zilch (Hrsg.): Raumordnung und Städtebau, Öffentliches Baurecht/Verkehrssysteme und Verkehrsanlagen. Springer, 2013, ISBN 978-3-642-41875-4, S. 2152 (eingeschränkte Vorschau in der Google-Buchsuche).

[7] ttps://mediatum.ub.tum.de/doc/1366901/1366901.pdf Alexander Tobias Lange: Gestaltung der Fahrdynamik beim Fahrstreifenwechselmanöver als Rückmeldung für den Fahrer beim automatisierten Fahren, Dissertation an der TUM 2017, abgerufen am 13. Feb. 2022

[8] Dietrich Wende: Fahrdynamik. Transpress VEB Verlag für Verkehrswesen, Berlin 1983, S. 15.