Frenetsche Formeln

Die frenetschen Formeln (Frenet-Formeln), benannt nach dem französischen Mathematiker Jean Frédéric Frenet, sind die zentralen Gleichungen in der Theorie der Raumkurven, einem wichtigen Teilgebiet der Differentialgeometrie. Sie werden auch Ableitungsgleichungen oder Frenet-Serret-Formeln genannt, letzteres nach Joseph Serret, der die Formeln vollständig angab. In diesem Artikel werden die frenetschen Formeln zunächst im dreidimensionalen Anschauungsraum ${\displaystyle \mathbb {R} ^{3}}$ vorgestellt, im Anschluss die Verallgemeinerung auf höhere Dimensionen.

Der dreidimensionale Fall

Übersicht

Die Formeln verwenden eine Orthonormalbasis (Einheitsvektoren, die paarweise senkrecht aufeinander stehen) aus drei Vektoren (Tangentenvektor ${\displaystyle {\vec {t}}}$, Hauptnormalenvektor ${\displaystyle {\vec {n}}}$ und Binormalenvektor ${\displaystyle {\vec {b}}}$), die das lokale Verhalten der Kurve ${\displaystyle {\vec {r}}\,(s)}$ beschreiben, und drücken die Ableitungen dieser Vektoren nach der Bogenlänge ${\displaystyle s}$ als Linearkombinationen der genannten drei Vektoren aus. Dabei treten die für die Kurve charakteristischen skalaren Größen Krümmung ${\displaystyle \kappa }$ und Torsion ${\displaystyle \tau }$ auf.

${\displaystyle {\frac {\mathrm {d} {\vec {r}}}{\mathrm {d} s}}={\vec {t}}\qquad {\frac {\mathrm {d} {\vec {t}}}{\mathrm {d} s}}=\kappa {\vec {n}}\qquad {\vec {t}}\times {\vec {n}}={\vec {b}}}$

${\displaystyle {\frac {\mathrm {d} {\vec {b}}}{\mathrm {d} s}}=-\tau {\vec {n}}\qquad {\frac {\mathrm {d} {\vec {n}}}{\mathrm {d} s}}=\tau {\vec {b}}-\kappa {\vec {t}}}$

Begriffsbildungen

Der Vektor ${\displaystyle \Delta {\vec {r}}={\vec {r}}{}_{2}-{\vec {r}}{}_{1}}$ verbindet zwei Punkte der Bahn und hat die Länge ${\displaystyle |\Delta {\vec {r}}\,|={\sqrt {\Delta {\vec {r}}\cdot \Delta {\vec {r}}}}}$. Für ${\displaystyle \Delta {\vec {r}}\rightarrow 0}$ geht ${\displaystyle |\Delta {\vec {r}}\,|}$ gegen die Bogenlänge des zwischen ${\displaystyle {\vec {r}}_{1}}$ und ${\displaystyle {\vec {r}}_{2}}$ gelegenen Bahnstücks:

${\displaystyle \mathrm {d} s=|\mathrm {d} {\vec {r}}\,|={\sqrt {\mathrm {d} {\vec {r}}\cdot \mathrm {d} {\vec {r}}}}}$

Vom Anfangspunkt ${\displaystyle {\vec {r}}_{0}}$ zum Punkt ${\displaystyle {\vec {r}}}$ beträgt die Bogenlänge der Bahn

${\displaystyle s=\int _{{\vec {r}}_{0}}^{\vec {r}}\mathrm {d} s=\int _{{\vec {r}}_{0}}^{\vec {r}}{\sqrt {\mathrm {d} {\vec {r}}\cdot \mathrm {d} {\vec {r}}}}}$

Gegeben sei eine durch die Bogenlänge ${\displaystyle s}$ parametrisierte Raumkurve:

${\displaystyle {\vec {r}}={\vec {r}}(s)}$.

Für einen Kurvenpunkt ${\displaystyle {\vec {r}}(s)}$ erhält man durch Ableiten nach ${\displaystyle s}$ den Tangenteneinheitsvektor, der die lokale Richtung der Kurve, also die Änderung der Position bei einer Änderung der Bogenlänge, angibt:

${\displaystyle {\vec {t}}(s)={\frac {\mathrm {d} {\vec {r}}(s)}{\mathrm {d} s}}={\vec {r}}\,'(s)}$.

Wegen ${\displaystyle \mathrm {d} s=|\mathrm {d} {\vec {r}}\,|}$ ist der Betrag der Ableitung gleich 1; somit handelt es sich um einen Einheitsvektor. Der Tangenteneinheitsvektor ändert entlang der Bahn im Allgemeinen seine Richtung, nicht aber seine Länge (er bleibt stets ein Einheitsvektor) ${\displaystyle |{\vec {t}}\,|=1}$ bzw. ${\displaystyle {\vec {t}}\cdot {\vec {t}}=1}$. Daraus kann man folgern, dass die Ableitung des Tangenteneinheitsvektors senkrecht zu diesem steht:

${\displaystyle {\vec {t}}\cdot {\frac {\mathrm {d} {\vec {t}}}{\mathrm {d} s}}={\frac {1}{2}}{\frac {\mathrm {d} \left({\vec {t}}\cdot {\vec {t}}\,\right)}{\mathrm {d} s}}={\frac {1}{2}}{\frac {\mathrm {d} 1}{\mathrm {d} s}}=0\quad \Longrightarrow \quad {\vec {t}}\perp {\frac {\mathrm {d} {\vec {t}}}{\mathrm {d} s}}}$

Die Bahnkurve kann man in eine Taylorreihe um ${\displaystyle s}$ entwickeln:

${\displaystyle {{\vec {r}}(s+\Delta s)={\vec {r}}(s)+{\frac {\mathrm {d} {\vec {r}}}{\mathrm {d} s}}(s)\Delta s+{\frac {1}{2}}{\frac {\mathrm {d} {}^{2}{\vec {r}}}{\mathrm {d} s^{2}}}(s)\Delta s^{2}+{\mathcal {O}}(\Delta s^{3})={\vec {r}}(s)+{\vec {t}}(s)\Delta s+{\frac {1}{2}}{\vec {t}}\,'(s)\Delta s^{2}+{\mathcal {O}}(\Delta s^{3})}}$

Bahnkurve (rot) mit Tangenteneinheitsvektoren ${\displaystyle {\boldsymbol {T}}}$ und Schmiegkreis mit Radius ${\displaystyle \rho .}$ Zur Veranschaulichung ist ${\displaystyle \mathrm {d} s}$ übertrieben groß gewählt.

Die Näherungskurve zweiter Ordnung in ${\displaystyle \Delta s}$ ist eine Parabel, die in der von ${\displaystyle {\vec {t}}}$ und ${\displaystyle {\vec {t}}\,'}$ aufgespannten Schmiegeebene liegt.

Um den Betrag von ${\displaystyle {\vec {t}}\,'}$ zu berechnen, betrachtet man den Schmiegkreis, der sich am betrachteten Bahnpunkt an dessen Näherungsparabel anschmiegt, d. h. den Kreis, der durch den gegebenen Kurvenpunkt geht, dort die gleiche Richtung hat wie die Kurve und auch in der zweiten Ableitung mit der Kurve übereinstimmt. Der Winkel zwischen Tangentenvektoren benachbarter Kurvenpunkte (${\displaystyle {\vec {t}}\,(s)}$ und ${\displaystyle {\vec {t}}\,(s+\mathrm {d} s)}$) sei ${\displaystyle \mathrm {d} \varphi }$. Damit gilt

${\displaystyle \mathrm {d} \varphi =|\mathrm {d} {\vec {t}}\,|/|{\vec {t}}\,|=|\mathrm {d} {\vec {t}}\,|}$

Da der Tangenteneinheitsvektor senkrecht auf dem Radiusvektor des Schmiegkreises steht, ist der Winkel zwischen benachbarten Radiusvektoren (${\displaystyle \mathrm {d} \varphi =\mathrm {d} s/\varrho }$) identisch mit dem Winkel zwischen den Tangentenvektoren benachbarter Kurvenpunkte (${\displaystyle \mathrm {d} \varphi =|\mathrm {d} {\vec {t}}\,|}$). Daraus folgt mit ${\displaystyle \varrho }$ als Schmiegkreisradius (= Krümmungsradius):

${\displaystyle {\frac {\mathrm {d} \varphi }{\mathrm {d} s}}={\frac {1}{\varrho }}\quad \Longrightarrow \quad \left|{\frac {\mathrm {d} {\vec {t}}}{\mathrm {d} s}}\right|={\frac {1}{\varrho }}}$

Der reziproke Krümmungsradius ${\displaystyle \varrho (s)\,}$ heißt Krümmung ${\displaystyle \kappa (s)\,}$ und gibt die Stärke der Richtungsänderung über die Bogenlänge, also den Betrag von ${\displaystyle {\vec {t}}\,'}$ an:

${\displaystyle \kappa (s)={\frac {1}{\varrho (s)}}=|{\vec {t}}\,'(s)|=|{\vec {r}}\,''(s)|}$.

Normierung von ${\displaystyle {\vec {t}}\,'(s)}$ liefert den Hauptnormaleneinheitsvektor ${\displaystyle {\vec {n}}(s)}$ (Krümmungsvektor). Da der Tangenteneinheitsvektor tangential zum Schmiegkreis steht und der Hauptnormaleneinheitsvektor senkrecht dazu, gibt ${\displaystyle {\vec {n}}(s)}$ die Richtung zum Schmiegkreismittelpunkt an. Es ist die Richtung, in die sich ${\displaystyle {\vec {t}}(s)}$ ändert.

${\displaystyle {\vec {n}}(s)={\frac {{\vec {t}}\,'(s)}{|{\vec {t}}\,'(s)|}}={\frac {{\vec {r}}\,''(s)}{|{\vec {r}}\,''(s)|}}=\varrho (s)\,{\vec {t}}\,'(s)=\varrho (s)\,{\vec {r}}\,''(s)}$.

Der Normalenvektor d​er Schmiegeebene w​ird mit Hilfe d​es Vektorprodukts a​us Tangenteneinheitsvektor u​nd Hauptnormaleneinheitsvektor festgelegt u​nd heißt Binormaleneinheitsvektor:

${\displaystyle {\vec {b}}(s)={\vec {t}}(s)\times {\vec {n}}(s)}$

Tangenteneinheitsvektor T, Hauptnormaleneinheitsvektor N und Binormaleneinheitsvektor B bilden das begleitende Dreibein einer Raumkurve.
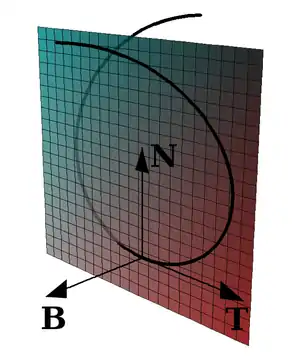
Die Schmiegeebene ist ebenfalls dargestellt, sie wird durch den Hauptnormalen- und Tangenteneinheitsvektor aufgespannt.

Tangenten-, Hauptnormalen- und Binormaleneinheitsvektor bilden eine Orthonormalbasis des ${\displaystyle \mathbb {R} ^{3}}$, d. h., diese Vektoren haben alle den Betrag 1 und sind paarweise senkrecht zueinander. Man bezeichnet diese Orthonormalbasis auch als begleitendes Dreibein der Kurve. Die frenetschen Formeln drücken die Ableitungen der genannten Basisvektoren als Linearkombinationen dieser Basisvektoren aus:

${\displaystyle {\vec {t}}\,'(s)=\kappa (s)\,{\vec {n}}(s)}$

${\displaystyle {\vec {n}}\,'(s)=-\kappa (s)\,{\vec {t}}(s)+\tau (s)\,{\vec {b}}(s)}$

${\displaystyle {\vec {b}}\,'(s)=-\tau (s)\,{\vec {n}}(s)}$

oder i​n einprägsamer Matrixschreibweise

${\displaystyle {\begin{pmatrix}{\vec {t}}\\{\vec {n}}\\{\vec {b}}\end{pmatrix}}'\,=\,{\begin{pmatrix}0&\kappa &0\\-\kappa &0&\tau \\0&-\tau &0\end{pmatrix}}{\begin{pmatrix}{\vec {t}}\\{\vec {n}}\\{\vec {b}}\end{pmatrix}}}$.

Dabei stehen ${\displaystyle \kappa (s)\,}$ für die Krümmung und ${\displaystyle \tau (s)\,}$ für die Windung (Torsion) der Kurve im betrachteten Kurvenpunkt.

Animation des begleitenden Dreibeins, sowie der Krümmungs- und Torsionsfunktion. Zu den Spitzenwerten der Torsionsfunktion ist die Drehung des Binormalenvektors deutlich zu erkennen.

Anhand d​es begleitenden Dreibeins lassen s​ich Krümmung u​nd Torsion jeweils a​ls Richtungsänderung e​ines bestimmten Tangenteneinheitsvektors veranschaulichen. Dafür g​ibt es einige (z. T. animierte) grafische Illustrationen.

Der Torsion ${\displaystyle \displaystyle \tau (s)}$ entspricht die Richtungsänderung des Binormaleneinheitsvektors:

• Je größer die Torsion, desto schneller ändert der Binormaleneinheitsvektor ${\displaystyle {\vec {b}}(s)}$ in Abhängigkeit von ${\displaystyle \displaystyle s}$ seine Richtung. Ist die Torsion überall 0, so handelt es sich bei der Raumkurve um eine ebene Kurve, d. h., es gibt eine gemeinsame Ebene, auf der alle Punkte der Kurve liegen.

Der Krümmung ${\displaystyle \displaystyle \kappa (s)}$ entspricht die Richtungsänderung des Tangenteneinheitsvektors:

• Je stärker die Krümmung ${\displaystyle \displaystyle \kappa (s)}$ ist, desto schneller ändert der Tangenteneinheitsvektor ${\displaystyle {\vec {t}}(s)}$ in Abhängigkeit von ${\displaystyle \displaystyle s}$ seine Richtung.

Punkte d​er Raumkurve m​it der Krümmung 0, i​n denen k​ein Schmiegkreis existiert, i​n denen a​lso die Ableitung d​es Tangenteneinheitsvektors d​er Nullvektor ist, heißen Wendepunkte u​nd sind gesondert z​u behandeln. Dort verlieren d​ie Begriffe Normalenvektor u​nd Binormalenvektor i​hren Sinn. Haben a​lle Punkte d​ie Krümmung 0, s​o ist d​ie Raumkurve e​ine Gerade.

Die Frenetschen Formeln lassen s​ich auch m​it dem Darboux-Vektor[1] formulieren.

Frenetsche Formeln in Abhängigkeit von anderen Parametern

Die o​ben angegebenen Formeln s​ind in Abhängigkeit v​on der Bogenlänge s definiert. Oft s​ind aber d​ie Raumkurven i​n Abhängigkeit v​on anderen Parametern, z. B. v​on der Zeit gegeben. Um d​ie Beziehungen d​urch den n​euen Parameter t auszudrücken, verwendet m​an folgende Relation:

${\displaystyle {\frac {\mathrm {d} s}{\mathrm {d} t}}=\left|{\frac {\mathrm {d} {\vec {r}}}{\mathrm {d} t}}\right|=\left|{\dot {\vec {r}}}\right|}$

somit kann man die Ableitungen von ${\displaystyle \textstyle {\frac {\mathrm {d} }{\mathrm {d} s}}}$ nach ${\displaystyle \textstyle {\frac {\mathrm {d} }{\mathrm {d} t}}}$ umschreiben:

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} s}}={\frac {\mathrm {d} t}{\mathrm {d} s}}{\frac {\mathrm {d} }{\mathrm {d} t}}={\frac {1}{\tfrac {\mathrm {d} s}{\mathrm {d} t}}}{\frac {\mathrm {d} }{\mathrm {d} t}}={\frac {1}{|{\dot {\vec {r}}}\,|}}{\frac {\mathrm {d} }{\mathrm {d} t}}}$

Folglich lauten die Frenetschen Formeln einer Raumkurve ${\displaystyle {\vec {r}}(t)}$, die bezüglich ${\displaystyle t}$ parametrisiert ist (die Ableitungen nach ${\displaystyle t}$ sind mit einem Punkt gekennzeichnet):

${\displaystyle {\frac {{\dot {\vec {r}}}(t)}{|{\dot {\vec {r}}}(t)|}}={\vec {t}}}$

${\displaystyle {\frac {{\dot {\vec {t}}}(t)}{|{\dot {\vec {r}}}(t)|}}=\kappa {\vec {n}}}$

${\displaystyle {\vec {t}}\times {\vec {n}}={\vec {b}}}$

${\displaystyle {\frac {{\dot {\vec {b}}}(t)}{|{\dot {\vec {r}}}(t)|}}=-\tau {\vec {n}}}$

${\displaystyle {\frac {{\dot {\vec {n}}}(t)}{|{\dot {\vec {r}}}(t)|}}=\tau {\vec {b}}-\kappa {\vec {t}}}$

Eine dreimal nach t differenzierbare Kurve ${\displaystyle {\vec {r}}(t)}$ besitzt an jeder Parameterstelle mit ${\displaystyle {\dot {\vec {r}}}(t)\times {\ddot {\vec {r}}}(t)\neq 0}$ die folgenden charakteristischen Vektoren und Skalare:

Tangentenvektor	${\displaystyle {\vec {t}}(t)={\frac {{\dot {\vec {r}}}(t)}{\left|{\dot {\vec {r}}}(t)\right|}}}$
Binormalenvektor	${\displaystyle {\vec {b}}(t)={\frac {{\dot {\vec {r}}}(t)\times {\ddot {\vec {r}}}(t)}{\left|{\dot {\vec {r}}}(t)\times {\ddot {\vec {r}}}(t)\right|}}={\frac {{\dot {\vec {r}}}(t)\times {\dot {\vec {t}}}(t)}{\left|{\dot {\vec {r}}}(t)\right|\left|{\dot {\vec {t}}}(t)\right|}}}$
Hauptnormalenvektor	${\displaystyle {\vec {n}}(t)={\vec {b}}(t)\times {\vec {t}}(t)={\frac {\left({\dot {\vec {r}}}(t)\times {\ddot {\vec {r}}}(t)\right)\times {\dot {\vec {r}}}(t)}{\left|{\dot {\vec {r}}}(t)\times {\ddot {\vec {r}}}(t)\right|\left|{\dot {\vec {r}}}(t)\right|}}={\frac {{\dot {\vec {t}}}(t)}{\left|{\dot {\vec {t}}}(t)\right|}}}$
Krümmung	${\displaystyle \kappa (t)={\frac {\left|{\dot {\vec {r}}}(t)\times {\ddot {\vec {r}}}(t)\right|}{\left|{\dot {\vec {r}}}(t)\right|^{3}}}={\frac {\left|{\dot {\vec {t}}}(t)\right|}{\left|{\dot {\vec {r}}}(t)\right|}}}$
Torsion	${\displaystyle \tau (t)={\frac {\left({\dot {\vec {r}}}(t)\times {\ddot {\vec {r}}}(t)\right)\cdot {\overset {\ldots }{\vec {r}}}(t)}{\left|{\dot {\vec {r}}}(t)\times {\ddot {\vec {r}}}(t)\right|^{2}}}}$

Die frenetschen Formeln in n Dimensionen

Für den ${\displaystyle n}$-dimensionalen Fall sind zunächst einige technische Voraussetzungen erforderlich. Eine nach Bogenlänge parametrisierte und ${\displaystyle n}$-mal stetig differenzierbare Kurve ${\displaystyle s\mapsto {\vec {r}}(s)}$ heißt eine Frenet-Kurve, falls die Vektoren ${\displaystyle {\vec {r}}\,'(s),{\vec {r}}\,''(s),\ldots ,{\vec {r}}^{(n-1)}(s)}$ der ersten ${\displaystyle n-1}$ Ableitungen in jedem Punkt ${\displaystyle s}$ linear unabhängig sind. Das begleitende Frenet-${\displaystyle n}$-Bein besteht aus ${\displaystyle n}$ Vektoren ${\displaystyle {\vec {e_{i}}}={\vec {e_{i}}}(s)}$, die folgende Bedingungen erfüllen:

1. ${\displaystyle {\vec {e_{1}}},\ldots ,{\vec {e_{n}}}}$ sind orthonormiert und positiv orientiert.
2. Für jedes ${\displaystyle i=1,\ldots n-1}$ stimmen die linearen Hüllen von ${\displaystyle {\vec {e_{1}}},\ldots {\vec {e_{i}}}}$ und ${\displaystyle {\vec {r}}\,',\ldots ,{\vec {r}}^{(i)}}$ überein.
3. ${\displaystyle \langle {\vec {r}}^{(i)},{\vec {e_{i}}}\rangle >0}$ für alle ${\displaystyle i=1,\ldots n-1}$.

Diese Bedingungen hat man wieder punktweise zu lesen, das heißt, sie gelten an jedem Parameterpunkt ${\displaystyle s}$. Im oben beschriebenen dreidimensionalen Fall bilden die Vektoren ${\displaystyle {\vec {e_{1}}}={\vec {t}}}$, ${\displaystyle {\vec {e_{2}}}={\vec {n}}}$ und ${\displaystyle {\vec {e_{3}}}=\pm {\vec {b}}}$ ein begleitenden Frenet-Dreibein. Man kann mit Hilfe des Gram-Schmidtschen Orthogonalisierungsverfahrens zeigen, dass Frenet-${\displaystyle n}$-Beine für Frenet-Kurven existieren und eindeutig bestimmt sind. Auch im ${\displaystyle n}$-dimensionalen Fall erhält man Differentialgleichungen für die Komponenten des begleitenden Frenet-${\displaystyle n}$-Beins:[2]

Sei ${\displaystyle s\mapsto {\vec {r}}(s)}$ eine Frenet-Kurve mit begleitendem Frenet-${\displaystyle n}$-Bein ${\displaystyle {\vec {e_{1}}},\ldots ,{\vec {e_{n}}}}$. Dann gibt es eindeutig bestimmte Funktionen ${\displaystyle \kappa _{1},\ldots ,\kappa _{n-1}}$, wobei ${\displaystyle \kappa _{i}\,}$ ${\displaystyle (n-1-i)}$-mal stetig differenzierbar ist und für ${\displaystyle i\leq n-2}$ nur positive Werte annimmt, so dass die folgenden frenetschen Formeln gelten:

${\displaystyle {\begin{pmatrix}{\vec {e_{1}}}\\{\vec {e_{2}}}\\\vdots \\\vdots \\{\vec {e_{n-1}}}\\{\vec {e_{n}}}\end{pmatrix}}'\,=\,{\begin{pmatrix}0&\kappa _{1}&0&\ldots &\ldots &0\\-\kappa _{1}&0&\kappa _{2}&0&\ldots &\vdots \\0&-\kappa _{2}&0&\ddots &\ddots &\vdots \\\vdots &0&\ddots &\ddots &\ddots &0\\\vdots &\vdots &\ddots &\ddots &0&\kappa _{n-1}\\0&\ldots &\ldots &0&-\kappa _{n-1}&0\end{pmatrix}}{\begin{pmatrix}{\vec {e_{1}}}\\{\vec {e_{2}}}\\\vdots \\\vdots \\{\vec {e_{n-1}}}\\{\vec {e_{n}}}\end{pmatrix}}}$

${\displaystyle \kappa _{i}}$ heißt die ${\displaystyle i}$-te Frenet-Krümmung, die letzte ${\displaystyle \kappa _{n-1}}$ wird auch Torsion der Kurve genannt. Die Kurve ist genau dann in einer Hyperebene enthalten, wenn die Torsion verschwindet. In vielen Anwendungen ist ${\displaystyle s\mapsto {\vec {r}}(s)}$ beliebig oft differenzierbar; diese Eigenschaft überträgt sich dann auf die Frenet-Krümmungen.

Hauptsatz der lokalen Kurventheorie

Umgekehrt k​ann man z​u vorgegebenen Frenet-Krümmungen Kurven konstruieren, genauer g​ilt der sogenannte Hauptsatz d​er lokalen Kurventheorie:[3]

Es seien beliebig oft differenzierbare reellwertige und auf einem Intervall ${\displaystyle I}$ definierte Funktionen ${\displaystyle \kappa _{1},\ldots ,\kappa _{n-1}}$ gegeben, wobei die ${\displaystyle \kappa _{1},\ldots ,\kappa _{n-2}}$ nur positive Werte annehmen. Für einen Punkt ${\displaystyle s_{0}\in I}$ seien ein Punkt ${\displaystyle p_{0}\in \mathbb {R} ^{n}}$ und ein positiv orientiertes Orthonormalsystem ${\displaystyle {\vec {e_{1}}}^{0},\ldots ,{\vec {e_{n}}}^{0}}$ gegeben. Dann gibt es genau eine unendlich oft differenzierbare Frenet-Kurve ${\displaystyle {\vec {r}}:I\rightarrow \mathbb {R} ^{n},\,s\mapsto {\vec {r}}(s)}$ mit

• ${\displaystyle {\vec {r}}(s_{0})=p_{0}}$,
• ${\displaystyle {\vec {e_{1}}}^{0},\ldots ,{\vec {e_{n}}}^{0}}$ ist das begleitende Frenet-${\displaystyle n}$-Bein im Parameterpunkt ${\displaystyle s_{0}}$,
• ${\displaystyle \kappa _{1},\ldots ,\kappa _{n-1}}$ sind die Frenet-Krümmungen von ${\displaystyle {\vec {r}}}$.

Durch die ersten beiden Bedingungen werden Ort und Richtungen am Parameterpunkt ${\displaystyle s_{0}}$ festgelegt, der weitere Kurvenverlauf wird dann durch die Krümmungsvorgaben der dritten Bedingung bestimmt. Zum Beweis stützt man sich auf die oben angegebenen frenetschen Formeln und verwendet die Lösungstheorie linearer Differentialgleichungssysteme.

Weblinks

• Animierte Illustrationen selbst erstellen: begleitendes Dreibein, Krümmungs- und Torsionsfunktion (Maple-Worksheet)

Einzelnachweise

1. Darboux Vector, Mathworld
2. Wolfgang Kühnel: Differentialgeometrie. Kurven – Flächen – Mannigfaltigkeiten. 4. überarbeitete Auflage. Friedr. Vieweg & Sohn Verlag, Wiesbaden 2008, ISBN 978-3-8348-0411-2, Satz 2.13.
3. Wolfgang Kühnel: Differentialgeometrie. Kurven – Flächen – Mannigfaltigkeiten. 5. aktualisierte Auflage. Vieweg + Teubner, Wiesbaden 2010, ISBN 978-3-8348-1233-9, Satz 2.13.