Hotellings Gesetz

Hotellings Gesetz ist ein Theorem in der Mikroökonomie. Es besagt, dass rational handelnde Produzenten versuchen, ihre Produkte so ähnlich wie möglich im Vergleich zu ihren Wettbewerbern zu gestalten. Hotellings Gesetz wird auch als das „Prinzip der minimalen Unterscheidung“ bezeichnet. Es wurde als erstes von Harold Hotelling im Jahre 1929 in seinem Aufsatz im Economic Journal „Stability in Competition“ erwähnt. Es gilt heute als überholt.[1]

Das gegenteilige Phänomen wird als (vertikale) Produktdifferenzierung bezeichnet.

Beispiel

Das Eisverkäufer-am-Strand-Problem beschreibt Hotellings Gesetz anhand des Standortfaktors und illustriert mögliche Strategien zweier Anbieter bei der Suche nach dem optimalen Standort. In einer Marktwirtschaft mit Wettbewerb stellt sich dabei heraus, dass das Endergebnis wäre, dass beide Eisverkäufer so nah wie möglich zusammenrücken.

Ausgangssituation: Beide Eisverkäufer befinden sich jeweils in der Mitte ihrer Hälften

Aktion: Der linke Eisverkäufer wandert nach rechts

Reaktion: Der rechte Eisverkäufer wandert nach links

Endergebnis bei Konkurrenz: Beide Eisverkäufer verkaufen in der Strandmitte

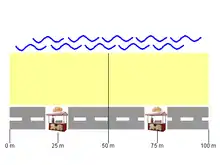
Ein Strand von 10 m Breite und 100 m Länge sei im Osten und Westen durch Felsen begrenzt, im Norden durch das Meer und im Süden durch eine Uferpromenade. An diesem Strand gibt es genau zwei Eisverkäufer mit je einem mobilen Eisverkaufsstand, der aber nur längs der Uferpromenade bewegt werden kann, nicht im Sand. Der Strand ist gleichmäßig mit Badegästen gefüllt. Beide Eisverkäufer bieten das gleiche Eis zum gleichen Preis an. Gesucht ist die optimale Position beider Eisverkäufer.

Lösung bei Kartell/Abstimmung

Die beiden Eisverkäufer wären optimal positioniert, wenn sie gleich große Einzugsgebiete hätten und so möglichst jeden Strandgast bedienten. Dafür gibt es genau die folgende Lösung:

Eisverkäufer $E_{1}$ positioniert sich $x$ Meter vom westlichen Rand entfernt, Eisverkäufer $E_{2}$ positioniert sich auf $100-x$ Meter. Beide haben jeweils 50 m Strand als ihr Einzugsgebiet. Das liegt daran, dass alle Badegäste aus dem Einzugsgebiet für $E_{1}$ es näher zu $E_{1}$ haben als zu $E_{2}$ . Alle Badegäste aus dem Einzugsgebiet für $E_{2}$ haben es näher zu $E_{2}$ als zu $E_{1}$ . Das Ganze funktioniert aber nur, wenn beide Eisverkäufer sich absprechen und ihre Absprache einhalten.

Als Beispiel sei hier $x=25$ genommen: $E_{1}$ steht auf 25 m, $E_{2}$ auf 75 m. (Dann haben die Strandgäste insgesamt gesehen die kürzesten Wege, was aber für das Problem keine Rolle spielt.)

Lösung bei Konkurrenz

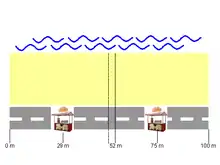
Wenn man davon ausgeht, dass beide Eisverkäufer $E_{1}$ und $E_{2}$ sich abgesprochen haben und sich anfangs auf ihrer optimalen Position befinden, wird eventuell, weil sie eigentlich in Konkurrenz zueinander stehen, sich in Eisverkäufer $E_{1}$ folgender Gedankengang abspielen: „Wenn ich mich ein bisschen mehr in Richtung $E_{2}$ bewege, dann wird mein Einzugsgebiet größer. Denn dann ist der Weg zu mir für mehr Badegäste als vorher kürzer. Er wird es schon nicht merken.“ Am nächsten Tag befindet sich E1 nicht mehr auf 25 m, sondern auf 29 m:

An diesem Tag, an dem sich $E_{1}$ auf 29 m befindet und $E_{2}$ auf 75 m, liegt die Mittellinie zwischen ihnen nicht mehr bei 50 m, sondern bei 52 m. Das heißt, dass das Einzugsgebiet von $E_{1}$ nicht mehr 50 m, sondern 52 m lang ist. Das Einzugsgebiet von $E_{2}$ ist nicht mehr 50 m, sondern nur noch 48 m lang. Entsprechend weniger Kunden erhält $E_{2}$ .

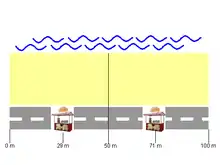
Spätestens jetzt merkt $E_{2}$ , dass es wahrscheinlich wichtig ist, selbst ein bisschen mehr in Richtung $E_{1}$ zu rücken, um das eigene Einzugsgebiet (wieder) zu vergrößern. Also rückt $E_{2}$ am nächsten Tag in Richtung $E_{1}$ :

An diesem dritten Tag hat sich die Mittellinie zwischen $E_{1}$ und $E_{2}$ entsprechend in Richtung $E_{1}$ bewegt. $E_{2}$ macht mehr Umsatz als $E_{1}$ . $E_{1}$ bemerkt, dass dies offensichtlich daran liegt, dass $E_{2}$ seinen Strandabschnitt vergrößert hat. Also repositioniert sich $E_{1}$ , um am folgenden Tag seinen Strandabschnitt zu vergrößern:

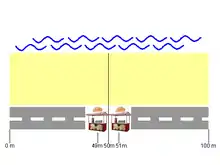
Dieses Spiel läuft einige Tage lang, bis sich die beiden Eisverkäufer in der Mitte treffen. Näher als ganz dicht zusammenrücken können sie nicht. Die Revierkämpfe hören also auf diese Weise auf. Das Einzugsgebiet der beiden Eisverkäufer ist wieder das gleiche wie am Anfang, keiner ist bevorteilt, es herrscht wieder ein „Gleichstand“, diesmal ist jedoch das Nash-Gleichgewicht erreicht.

Unter der Voraussetzung, dass es eine maximale Weglänge gibt, die die Badegäste bereit sind, für ihr Eis zurückzulegen, diese allerdings so groß ist und die Gäste so verteilt sind, dass sich an der oben vorausgesetzten Vorteilhaftigkeit der Entscheidung, sich zur Mitte zu bewegen, nichts ändert, ergeben sich folgende Konsequenzen:

Für die Badegäste, die sich ganz am Rand des Strands befinden, ist der Weg zu den Eisverkäufern nun zu weit. Obwohl sie ein Eis kaufen wollen, werden sie sich keines kaufen, wenn sie dafür so weit durch den heißen Sand laufen müssen.
Beide Eisverkäufer machen deswegen weniger Umsatz als vorher.

Ganz klar wäre die Situation, wie man sie am Anfang hatte, Pareto-optimal, sowohl für die Eisverkäufer als auch für die Badegäste. Aber die beschriebene Strategie der Eisverkäufer hat allen Beteiligten, außer den Kunden in der Mitte des Strandes, nur geschadet. Einen ähnlichen Prozess schildert das Braess-Paradoxon.

Unter der (zusätzlichen) Annahme, dass die Gesamtumsätze der Verkäufer sinken, weil die Kunden am Rand zu weit laufen müssten und lieber auf Eis verzichten, entsteht aus der Sicht der Verkäufer eine dem Gefangenendilemma ähnliche Situation. Sie unterscheidet sich aber insofern von diesem Modell, als die Entscheidungsvariable (Standort) kontinuierlich ist und nicht diskret („betrügen“ vs. „kooperieren“). Nimmt man an, dass der Gesamtumsatz konstant bleibt, gibt es keine Parallele zum Gefangenendilemma, sondern nur eine Verschlechterung der Zugangsbedingungen für die Kunden.

Bedeutung des Modells und Kritik

Das Modell dient der Illustration der Frage nach der optimalen Standortsuche unter marktwirtschaftlichen Bedingungen. Oft wird eingewandt, der Eisverkäufer würde bei der Wanderung nach rechts mehr Kunden auf der linken Seite verlieren, als er auf der rechten Seite gewinnen kann. Je nach Kundenverhalten ist dies jedoch nicht zwingend der Fall. Die Neue Institutionenökonomik befasst sich mit Problemen wie diesem und bietet Lösungen über die Einführung von Institutionen.

Ergänzung: All down | All up

Mit Bezug auf die ökonomische Wohlfahrt gibt es noch die Betrachtung von Ereignissen bei Veränderungen von relevanten Faktoren in dem Modell. Annahme: Wenn bei mehreren Anbietern sich bei einem Anbieter der Preis senkt, kann dieser seinen Absatzmarkt vergrößern. Daraus resultiert, dass dieser einen Teil des Absatzmarktes, den er vor der Preisveränderung sich mit einem anderen Anbieter teilte, zu eigen macht.

Der Anbieter mit dem gleichbleibenden höheren Preis hat nun einen Verlust von der Konsumentenrente, Produzentenrente und der gesamten Wohlfahrt zu verzeichnen – All down.
Der Anbieter mit dem neuen Preis, der nun unter dem alten liegt, kann seine Produzentenrente, seine Konsumentenrente und die gesamte Wohlfahrt erhöhen – All up.

Literatur

Harold Hotelling: Stability in Competition. Economic Journal 39: 41–57, (1929)

Weblinks

Einzelnachweise

C. d'Aspremont, J. Jaskold Gabszewicz, J.-F. Thisse: On Hotelling's "Stability in Competition". In: Econometrica. Band 47, Nr. 5, September 1979, S. 1145, doi:10.2307/1911955, JSTOR:1911955.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] C. d'Aspremont, J. Jaskold Gabszewicz, J.-F. Thisse: On Hotelling's "Stability in Competition". In: Econometrica. Band 47, Nr. 5, September 1979, S. 1145, doi:10.2307/1911955, JSTOR:1911955.