Extensivform eines Spiels
Die Extensivform eines Spiels, kurz Extensivform, ist in der Spieltheorie eine Darstellungsform von Spielen, die im Gegensatz zur Normalform eines Spiels die zeitliche Abfolge von Entscheidungen berücksichtigt und hierzu eine Spielbaum genannte Baumdarstellung verwendet.
Definition
Bei der Extensivform eines Spiels handelt es sich um eine mathematisch formale Beschreibung eines Spiels, mit der die gemäß der Spielregel möglichen Spielverläufe vollständig charakterisiert werden. Konkret handelt es sich um die folgenden Angaben:[1]
- Die Anzahl der Mitspieler.
- Zu jedem Spielstand (Position genannt) die Angaben darüber,
- wer am Zug ist,
- welche Zugmöglichkeiten für den betreffenden Spieler bestehen und
- auf Basis welcher Informationen (z. B. der Kenntnis der eigenen und der bereits ausgespielten Karten) er seine Entscheidung zu treffen hat.
- Für Endpositionen, wer wie viel gewonnen hat (der Gewinn eines Spielers wird Auszahlung genannt).
- Bei Zufallszügen, wie wahrscheinlich die möglichen Ergebnisse sind und wie sie gegebenenfalls untereinander korreliert sind.
Die Formalisierung der Extensivform beruht auf einem mathematischen Graphen, wobei die Knoten den Positionen und die Kanten den Zugmöglichkeiten entsprechen. Konkret beinhaltet diese Formalisierung[2]
- einen Baum (das ist ein zusammenhängender Graph ohne Schleifen),
- einen Knoten, der die Wurzel des Baums darstellt und die Anfangsposition des Spiels symbolisiert (und den Baum zu einem gerichteten Graphen macht),
- eine Menge von Spielern (darunter gegebenenfalls einen fiktiven Spieler, der die Zufallszüge „entscheidet“),
- eine Zuordnung, die jedem Knoten einen Spieler zuordnet (der in dieser Position zieht, das heißt einen erlaubten Zug auswählt),
- für jeden Spieler eine Partition der Knoten, in denen er zieht, in Informationsmengen,
- eine Zuordnung, die jedem Endknoten eine Auszahlung für jeden Spieler zuordnet.
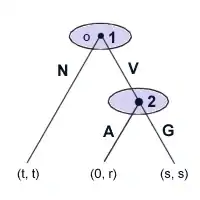
Die Informationsmengen beinhalten jeweils jene Knoten (auch als Entscheidungsknoten bezeichnet), die für den ziehenden Spieler aufgrund der ihm aktuell vorliegenden Information nicht unterscheidbar sind – zum Beispiel, weil die vorangehende Verzweigung innerhalb des Spielbaums auf einer für den ziehenden Spieler nicht erkennbaren Entscheidung eines anderen Spielers beruht. Alle Knoten einer Informationsmenge müssen daher die gleiche Anzahl von Zugmöglichkeiten beinhalten. Innerhalb der Extensivform müssen die Zugmöglichkeiten aller Knoten einer Informationsmenge jeweils übereinstimmend gekennzeichnet sein (beispielsweise durch eine Nummerierung). Innerhalb einer graphischen Darstellung des Spielbaums werden die Knoten der einzelnen Informationsmengen meist wie oben abgebildet zusammengefasst. Aufgrund dieser Darstellung spricht man auch von Informationsbezirken.
Ein Spiel, dessen sämtliche Informationsmengen nur jeweils ein Element enthalten, wird ein Spiel mit perfekter Information genannt. Manche Autoren sprechen auch von vollkommener Information. Ein ziehender Spieler kennt dann, wie bei den meisten Brettspielen üblich, stets die gesamte Vorgeschichte der aktuellen Partie. Gegenbeispiele sind Kartenspiele, bei denen die Spieler jeweils nur ihre eigenen Karten kennen. Solche Spiele sind Beispiele für Spiele mit imperfekter (bzw. unvollkommener) Information.
Auch ein Spiel mit imperfekter Information kann vollständige Information besitzen, was bedeutet, dass bei den Spielern Sicherheit über die Spielregeln besteht.
Eigenschaften von Spielen und deren Darstellung
Der Unterschied zwischen der Darstellung in Extensivform und jener in Normalform besteht darin, dass in der Extensivform ein Spiel als Abfolge von Entscheidungen der Spieler modelliert wird, während in der Normalform alle Entscheidungen als gleichzeitig stattfindend betrachtet werden.
Sequentielle Strukturen von Spielen machen Lösungskonzepte erforderlich, die über das Nash-Gleichgewicht hinausgehen. Insbesondere können Nash-Gleichgewichte Drohungen enthalten, die unglaubwürdig sind, wenn man die sequentielle Struktur des Spiels berücksichtigt. Eine Möglichkeit, solche Gleichgewichte auszuschließen, besteht in der Anwendung des Konzepts der teilspielperfekten Gleichgewichte.
Einzelnachweise
- Jörg Bewersdorff: Glück, Logik und Bluff: Mathematik im Spiel - Methoden, Ergebnisse und Grenzen, Vieweg+Teubner Verlag, 5. Auflage 2010, ISBN 3834807753, doi:10.1007/978-3-8348-9696-4, S. IX.
- Christian Rieck: Spieltheorie, Gabler, Wiesbaden 1993, ISBN 340916801X, S. 84–97.
Literatur
- Alós-Ferrer, Carlos/Ritzberger, Klaus (2005): Trees and Decisions, in: Economic Theory 25 (4): 763–798.
- Fudenberg, Drew/Tirole, Jean (1991): Game Theory. Cambridge (Mass.): MIT Press.
- Gibbons, Robert (1999): A Primer in Game Theory. Harlow: Pearson Education.
- Eichberger, Jürgen (1993): Game Theory for Economists. New York: Academic Press.