Unberechenbarkeit (Spieltheorie)
Die Unberechenbarkeit eines Spiels im spieltheoretischen Sinn entspricht der Ungewissheit, welcher die Spieler (und ggf. Zuschauer) eines Gesellschaftsspiels im Hinblick auf den Verlauf und das Resultat einer Partie ausgesetzt sind. Die Begriffe Unberechenbarkeit und Ungewissheit werden – wie auch der Begriff Spiel – in der Fachliteratur je nach Kontext (mathematische Spieltheorie, Soziologie, Politologie) mit uneinheitlicher Bedeutung verwendet.
Ursachen
Die Unberechenbarkeit des Spielverlaufs resultiert bei fast allen Spielen aus nur drei verschiedenen Ursachen, deren Differenzierung eine Klassifikation von Spielen ermöglicht:[1][2][3]
- Zufall wie bei Würfelspielen,
- eine hohe Zahl von Kombinationen, zu der sich die Zugmöglichkeiten der Spieler wie beim Schach kombinieren,
- verdeckte Information, etwa dadurch bedingt, dass jeder Spieler nur seine eigenen Karten kennt.
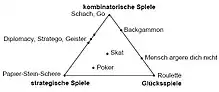
Innerhalb dieses Klassifikationsschemas können die Anteile, mit denen die drei Ursachen für ein konkretes Spiel das Spielergebnis bestimmen, in der Regel nur qualitativ bewertet werden. Zur Visualisierung eines Vergleichs verschiedener Spiele wird oft ein Dreieck[4][5] (auch bezeichnet als Bewersdorff-Dreieck,[6][7] Spannungsdreieck[8] oder Glück-Logik-und-Bluff-Dreieck[9]), gelegentlich auch eine Punkteskala[10] verwendet.
1. Zufall
Dieses Merkmal wird in Gesellschaftsspielen hauptsächlich durch Würfeln oder das Mischen von Spielkarten und -steinen verursacht. Die jeweilige Partie wird dann im Rahmen der Spielregeln sowohl durch die Entscheidungen der Spieler als auch durch zufällige Ereignisse bestimmt. Dominiert der Einfluss des Zufalls, handelt es sich um ein Glücksspiel. Bei reinen Glücksspielen ist die Entscheidung des Spielers über die Teilnahme sowie über die Höhe des Einsatzes bereits die wichtigste. Glücksspiele, die um Vermögenswerte gespielt werden, sind traditionell gesetzlichen Reglementierungen unterworfen, in Deutschland in Form eines Glücksspielmonopols.
- Beispiele für reine Glücksspiele: Roulette, Lotto, Spielautomaten.
2. Vielfältige Kombinationen der möglichen Züge
Die Spielregel räumt den Spielern die Möglichkeit ein, innerhalb eines genau vorgegebenen Rahmens zu agieren. Die Sequenz der Spieleraktionen, von denen eine einzelne als Zug bezeichnet wird, kombinieren sich zu einer meist großen Zahl von Zugfolgen, wodurch das Ergebnis einer Partie de facto unvorhersehbar wird. Spiele, bei denen die Ungewissheit ausschließlich auf diesem Phänomen beruht, werden als kombinatorische Spiele bezeichnet (solche Spiele für zwei Mitspieler werden z. T. in der Kombinatorischen Spieltheorie untersucht).
- Beispiele für kombinatorische Spiele: Schach, Go, Mühle, Dame und Halma.
- Beispiele für Spiele mit kombinatorischen und zufälligen Elementen: Backgammon und Mensch ärgere Dich nicht.
3. Unterschiedlicher Informationsstand der einzelnen Spieler
Eine weitere Ursache der Unberechenbarkeit beruht auf unterschiedlichen Informationsständen der agierenden Spieler, wie sie durch verdeckte Karten, verdeckt bleibende oder simultane Züge zustande kommen. Spiele, deren Ungewissheit vorwiegend von unterschiedlichen Informationsständen herrühren, werden strategische Spiele genannt.
- Beispiel für ein rein strategisches Spiel: Schere-Stein-Papier
- Spiele, in denen die Spieler unterschiedliche Informationsstände besitzen: Poker, Bridge, Spekulation an der Börse, Sport-Toto.
Mathematische Ansätze
Mit Mitteln der Mathematik wird versucht, die Unberechenbarkeit in Spielen im gewissen Rahmen zu überwinden. Gesucht sind optimale Verhaltensweisen für die Spieler. Je nach Ursache der Unberechenbarkeit sind die betreffenden Methoden unterschiedlichen Disziplinen der Mathematik und Informatik zuzuordnen:
- Wahrscheinlichkeitsrechnung,
- Kombinatorische Spieltheorie sowie Künstliche Intelligenz (z. B. betreffend Computerschach),
- Spieltheorie.
Grundlage der spieltheoretischen Untersuchungen ist ein formales Modell für Spiele, in dessen Rahmen Strategien untersucht werden.
Beispiel: Kopf oder Zahl (Matching Pennies)
Zwei Spieler wählen voneinander unabhängig die Seite einer zu werfenden Münze, das heißt entweder Kopf (K) oder Zahl (Z). Der erste Spieler gewinnt einen Euro, wenn Übereinstimmung erzielt wird. Falls unterschiedliche Ergebnisse erzielt werden, gewinnt der zweite Spieler einen Euro. Um das strategische Verhalten nicht vorhersehbar (berechenbar) zu machen, sollte ein Spieler zwischen den gegebenen Alternativen zufällig auswählen und damit eine so genannte gemischte Strategie verwenden.[11]
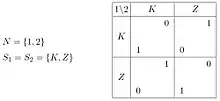
Erläuterungen:
- N = {Spieler 1, Spieler 2}
- Mögliche Strategie S1: Kopf
- Strategieräume S1 = S2 = {Kopf, Zahl}
- Mögliches Profil: s = (Zahl, Zahl)
- Menge aller Strategieprofile: S = {(Kopf,Zahl);(Kopf,Kopf);(Zahl,Kopf);(Zahl,Zahl)}
Mathematische Spieltheorie
In ihrem Spieltheorie-Buch erläutern Dixit und Nalebuff in einem mit Unberechbarkeit betitelten Kapitel gemischte Strategien in Spielen.[12] Eine gemischte Strategie ist eine Zufallsauswahl mit einer zu Beginn des Spiels festgelegten Wahrscheinlichkeitsverteilung, mit der ein vollständiger Handlungsplan des Spielers „ausgewürfelt“ wird, der für jede im Spiel möglicherweise anstehende Entscheidungssituation eine Entscheidung beinhaltet. Die Unberechenbarkeit resultiert also in diesem Fall nicht direkt auf dem Spiel, sondern auf den gegebenenfalls durch das Spiel motivierten Verhaltensweisen der entsprechend agierenden Spieler.
Bei einem Zwei-Personen-Nullsummenspiel, das sich dadurch auszeichnet, dass der Gewinn des einen Spielers stets gleich dem Verlust seines Kontrahenten ist, existiert auf Basis gemischter Strategien stets ein Gleichgewicht mit einem eindeutig bestimmten Spielresultat (Min-Max-Theorem). Solche Minimax-Strategien sind im Prinzip mit Verfahren der linearen Optimierung berechenbar. Für Spiele mit mehr als zwei Personen oder Zwei-Personen-Spiele ohne Nullsummencharakter kann es mehrere Gleichgewichte mit unterschiedlichen Spielresultaten geben (sog. Nash-Gleichgewichte).[13]
Ökonomische Anwendungen der Spieltheorie
Eigentlicher Fokus spieltheoretischer Untersuchungen ist nicht die Verhaltensoptimierung in Gesellschaftsspielen. So formulierte bereits 1928 der Begründer der Spieltheorie John v. Neumann: „... es gibt wohl kaum eine Frage des täglichen Lebens, in die dieses Problem nicht hineinspielte.“[14]
Allerdings wird die praktische Relevanz der Spieltheorie von Politologen wie Joachim Raschke und Ralf Tils aufgrund ihres „realistätsfernen Reduktionismus“ bestritten: „Die Spieltheorie bleibt – außer in Randbereichen – folgenlos für die Praxis.“[15]. Zur Unberechenbarkeit bemerken die Autoren auf ihrer nicht spieltheoretischen Betrachtungsebene: „Falsch ist die Annahme prinzipieller Unberechenbarkeit – dann wäre auch Strategie nicht möglich. Es existieren Grade der Berechenbarkeit. Strategie wird unberechenbarer, je größere Spielräume eine Institution ermöglicht... Strategie nimmt Bezug auf die berechenbaren Dimensionen externer Akteuere. Man kann ... mögliches Gegnerverhalten antizipieren und Reaktions-Reserven dafür aufbauen“.[16]
Generell ist es vorteilhaft, die Unberechenbarkeit des Kontrahenten richtig vorauszusagen und entsprechend handeln zu können. Die Unberechenbarkeit wird zu einem entscheidenden Teil der Strategie, wenn einer der Mitspieler ein simultanes Vorgehen wünscht und der andere Mitspieler dieses lieber verhindern möchte.[17][18]
Damit ist die Unberechenbarkeit ein unerlässlicher Bestandteil der Realität und bildet dadurch einen Ausgangspunkt des unternehmerischen Handelns, es ist kein nachteiliger Bestandteil, welcher durch den planenden und handelnden Menschen eliminiert werden muss, er muss mit ihm umgehen können und für sich den entsprechenden Mehrwert ziehen.[19]
- Beispiel 1: Unberechenbarkeit beim Streik
Innerhalb eines Streiks von Mitarbeitern der Müllabfuhr musste eine neue Streikstrategie entwickelt werden, da der bis dahin sechswöchige Streik zu keinem Ergebnis führte und die Beteiligten erste Ermüdungserscheinungen vorwiesen. Die Streikstrategie musste so geändert werden, dass diese für die Gegenseite nicht vorhersehbar war, das heißt unberechenbar. Die Mitarbeiter einigten sich auf den Streikversammlungen, die Streikaktivitäten geändert fortzusetzen. Sie entwickelten eine Strategie, die es dem Arbeitgeber erschweren sollte, private Müllabfuhrunternehmer einzusetzen. Die Streiktaktik sah vor, mittels abgestimmter Absprache die Arbeitgeber im Unklaren zu lassen, wann und wie lange gestreikt wird. Die Arbeitgeber wurden davon überrumpelt und konnten auf die ständig wechselnde Situation nicht rechtzeitig reagieren. Die veränderte unberechenbare Streikstrategie war erfolgreich.[20]
- Beispiel 2: Finanzamt
Überprüfung von Steuerzahlern durch das Finanzamt, ob genügend Steuern gezahlt wurden, während der zu Überprüfende dieser lieber entgehen würde.[21]
Soziologische Aspekte
Für Roger Caillois ist die Ungewissheit neben Freiwilligkeit, Unproduktivität, Begrenztheit in Raum und Zeit, Regelbestimmtheit und Fiktivität eines der sechs Merkmale eines Spiels. In seiner darauf aufbauenden Spiel-Typisierung in Wettkampf, Zufall, Rausch und Maskierung wird insbesondere dem Zufall die Unberechenbarkeit zugeordnet: „Unberechenbarkeit meint das strukturelle Merkmal Zufall oder Glück (alea), was besonders die Spannung auszumachen scheint bzw. selbst solch eine permanent erzeugen kann: Ob etwas Neues gelingt oder wer diesmal gewinnt, sich taktisch klug verhält... – Damit scheinen Spiele unendlich wiederholbar zu sein, da sie nicht vorausberechnet werden können und immer "anders" sind“[22].
Ausgewählte Zitate zur Unberechenbarkeit
„Man muss dem Zufall seinen Spielraum lassen, weil man ihn nie ganz beherrschen kann, sondern, indem man ihn zu beschränken sucht, sein Gebiet vielmehr erweitert…“ Gerhard von Scharnhorst[23]
„Das Glück hilft dem nicht, der sich nicht anstrengt“ Leonardo da Vinci[23]
Weblinks
- Zukunftswerkstätten – Was macht Spaß am Spiel? Zukunftswerkstätten Jahrestreffen 2005
- Plädoyer für Unberechenbarkeit im Streik (Memento vom 27. Dezember 2010 im Internet Archive)
- stern.de – Die Kunst des Verblüffens
- Webseite von Jörg Bewersdorff – Die Mathematik von Gesellschaftsspielen
- QUAAK! – Online-Spiel zur Minimax-Strategie
Literatur
- Avinash K. Dixit, Barry J. Nalebuff: Spieltheorie für Einsteiger – Strategisches Know-how für Gewinner, Schäffer-Poeschel Verlag Stuttgart, 1995, ISBN 3-7910-0913-3
- Jörg Bewersdorff: Glück, Logik und Bluff: Mathematik im Spiel – Methoden, Ergebnisse und Grenzen, Wiesbaden 1998; 6. Auflage 2012, ISBN 978-3-8348-1923-9, doi:10.1007/978-3-8348-2319-9.
- Hans H. Hinterhuber: Wettbewerbsstrategie, Berlin 1990, ISBN 3-11-0099-43-8, doi:10.1515/9783110854640
- Christian Rieck: Spieltheorie: Eine Einführung, Christian Rieck Verlag, Eschborn, 2006, ISBN 3-924043-91-4
- Joachim Raschke, Ralf Tils: Politische Strategie: Eine Grundlegung, Wiesbaden 2007, ISBN 3-53-1149-56-3, doi:10.1007/978-3-531-90410-8
- Peter-Jürgen Jost: Die Spieltheorie in der Betriebswirtschaftslehre, Stuttgart, 2001, ISBN 3-7910-1778-0
Belege
- Jörg Bewersdorff: Glück, Logik und Bluff: Mathematik im Spiel - Methoden, Ergebnisse und Grenzen, Wiesbaden 1998, ISBN 978-3-528-06997-1, S. V-VIII (Springer-Link)
- Hartmut Menzer, Ingo Althöfer: Zahlentheorie und Zahlenspiele: Sieben ausgewählte Themenstellungen, München 2014, ISBN 978-348672030-3, S. 321 in der Google-Buchsuche, doi:10.1524/9783486720310.321
- Tom Verhoeff, The Mathematical Analysis of Games, Focusing on Variance, : MaCHazine, 13(3), März 2009. Eine ausführliche Version erschien in Niederländisch: Spelen met variantie, Pythagoras, 49(3), Januar 2010, S. 20–24.
- Jörg Bewersdorff: Glück, Logik und Bluff: Mathematik im Spiel - Methoden, Ergebnisse und Grenzen, Wiesbaden 1998, ISBN 978-3-528-06997-1, S. VII (Springer-Link)
- Dagmar de Cassan: Das Buch der Spiele 2005 (online)
- Hartmut Menzer, Ingo Althöfer: Zahlentheorie und Zahlenspiele: Sieben ausgewählte Themenstellungen, München 2014, ISBN 978-348672030-3, S. 322 in der Google-Buchsuche, doi:10.1524/9783486720310.321
- Petter Øgland: Implementing Lean ISO 9001 in Public Administration. Lulu Press, ISBN 978-1-71680-514-1, Using Lean Development strategies for getting good at Pac-Man: Results from six years of daily training, S. 123, 125, 138 (researchgate.net).
- Hugo Kastner: Mit Spielen lernen: Ratgeber für Eltern, Erzieher und Lehrer, Hannover 2010, ISBN 978-3-86910-609-0, S. 239 in der Google-Buchsuche
- Nils Hesse: Spielend gewinnen: Gewinnstrategien für die 50 bekanntesten Karten-, Würfel-, Brett- und Gewinnspiele, Wiesbaden 2015, ISBN 978-3-658-04440-4, S. X in der Google-Buchsuche, doi:10.1007/978-3-658-04441-1
- WIN, das Spielejournal, Jänner 2014, ISSN 0257-361X, S. 36 f. (online)
- Peter-Jürgen Jost: Die Spieltheorie in der Betriebswirtschaftslehre, Stuttgart, 2001, S. 51 f.
- Avinash Dixit, Barry J. Nalebuff: Spieltheorie für Einsteiger. Strategisches Know-how für Gewinner, Ulm 1997, S. 165 ff.
- Christian Rieck: Spieltheorie - eine Einführung, Eschborn 2006, S. 95, S. 282
- J. v. Neumann: Zur Theorie der Gesellschaftsspiele, Mathematische Annalen, 100 (1928), S. 295–320 (Digi-Zeitschriften).
- Joachim Raschke, Ralf Tils: Politische Strategie: Eine Grundlegung, Wiesbaden 2007, S. 77, doi:10.1007/978-3-531-90410-8
- Joachim Raschke, Ralf Tils: Politische Strategie: Eine Grundlegung, Wiesbaden 2007, S. 153, doi:10.1007/978-3-531-90410-8
- Avinash Dixit: Spieltheorie für Einsteiger. Strategisches Know-how für Gewinner, Ulm 1997, S. 165
- Hans H. Hinterhuber: Wettbewerbsstrategie, Berlin 1990, S. 82, doi:10.1515/9783110854640
- Hans H. Hinterhuber: Wettbewerbsstrategie, Berlin 1990, S. 81, doi:10.1515/9783110854640
- Plädoyer für Unberechenbarkeit im Streik (Memento vom 27. Dezember 2010 im Internet Archive)
- Avinash Dixit: Spieltheorie für Einsteiger. Strategisches Know-how für Gewinner, Ulm 1997. S. 165
- Was macht Spaß am Spiel? Zukunftswerkstätten Jahrestreffen 2005 (Protokoll)
- Hans H. Hinterhuber: Wettbewerbsstrategie, Berlin 1990, S. 66, doi:10.1515/9783110854640