Spiel mit perfekter Information

Spiel mit perfekter Information, manchmal auch Spiel mit vollkommener Information genannt,[1] ist ein Begriff der mathematischen Spieltheorie. Demnach besitzt ein Spiel perfekte Information, wenn jedem Spieler zum Zeitpunkt einer Entscheidung stets das vorangegangene Spielgeschehen, d. h. die zuvor getroffenen Entscheidungen seiner Mitspieler sowie die zuvor getroffenen Zufallsentscheidungen, bekannt sind.[2]

Unter den Gesellschaftsspielen besitzen die meisten klassischen Brettspiele perfekte Information. Beispiele sind Go, Schach, Dame, Mühle, Halma, Nim und Mancala als Zweipersonenspiele oder auch Solitär und SameGame als Solitairespiel. Auch Spiele mit Zufallseinfluss wie Backgammon und Mensch ärgere Dich nicht, letzteres unabhängig von der Anzahl der Spieler, besitzen perfekte Information.

Ein Spiel ohne perfekte Information wird auch als Spiel mit imperfekter Information bezeichnet. Beispiele sind Kartenspiele wie Skat und Poker, weil dort jeder Spieler nur seine eigenen Karten kennt. Auch ein Spiel mit gleichzeitigen Zügen wie Schere, Stein, Papier ist kein Spiel mit perfekter Information, da dem sich entscheidenden Spieler die simultan erfolgende Entscheidung des Kontrahenten nicht bekannt ist. Insofern sind Informationsstände, die bezogen auf die Spieler asymmetrisch sind, kennzeichnend für Spiele mit imperfekter Information.

Eigenschaften

1912 bewies Ernst Zermelo, dass ein endliches Zwei-Personen-Nullsummenspiel mit perfekter Information und ohne Zufallseinfluss ein eindeutig bestimmtes Spielergebnis besitzt, und zwar in dem Sinn, dass der eine Spieler mindestens dieses Ergebnis unabhängig von der Spielweise des Kontrahenten erzwingen kann, während es dem Kontrahenten möglich ist, ein noch höheres Ergebnis zu verhindern.[3] Für das von Zermelo beispielhaft betrachtete Schachspiel bedeutet dies konkret, dass Schach entweder

wie bei einer Problemstellung Weiß eine Gewinnstrategie erlaubt, oder aber
Schwarz eine solche Gewinnstrategie besitzt, oder aber
beide Spieler für sich jeweils mindestens ein Remis erzwingen können.

Man nennt solche Spiele auch determiniert.

Angewendet auf eine Hin- und Rückpartie mit vertauschten Farben hat Zermelos Satz zur Konsequenz, dass ein Spieler mit fehlerfreiem Spiel mindestens ein ausgeglichenes Gesamtergebnis erzwingen kann – aber auch nicht mehr, wenn der Kontrahent ebenfalls fehlerfrei spielt.

Das bei beidseitig fehlerfreiem Spiel entstehende Spielergebnis wird als Wert des Spiels bezeichnet. Seine praktische Bestimmung kann für ein gegebenes Spiel sehr schwierig sein, auch wenn mit dem Minimax-Algorithmus theoretisch immer eine Berechnungsmöglichkeit besteht. Zahlreiche Spiele, darunter Dame, Mühle und Vier gewinnt, sind mittlerweile vollständig gelöst und die entsprechenden Strategien sind bekannt. Für einige Spiele wie zum Beispiel Hex sind nur die Werte der Anfangsposition aufgrund von Symmetrieüberlegungen bestimmbar, ohne dass man zugehörige Strategien kennt.

Spiele einer speziellen Unterklasse werden innerhalb der sogenannten Kombinatorischen Spieltheorie untersucht.

Für ein endliches Zwei-Personen-Nullsummenspiel mit perfekter Information und Zufallseinfluss gilt Zermelos Satz analog in Bezug auf den Erwartungswert des Gewinns. Das heißt, ein Spieler besitzt eine Strategie, so dass der Erwartungswert seines Gewinns mindestens diesen Wert erreicht, während für seinen Kontrahenten eine Strategie existiert, welche die Gewinnerwartung des ersten Spielers auf maximal diesen Wert begrenzt. Folglich besitzt beispielsweise jede Position des Backgammon, das streng genommen auf eine endliche Länge begrenzt werden muss, einen eindeutig definierten Wert.

Für endliche Spiele mit perfekter Information, die mit mehr als zwei Personen gespielt werden oder die keinen Nullsummen-Charakter aufweisen, gilt Zermelos Satz nicht. Das heißt, für solche Spiele lassen sich im Allgemeinen keine objektiv besten Strategien finden. Allerdings existieren nach einem Satz von Harold Kuhn aus dem Jahr 1950 Gleichgewichte in reinen Strategien.[4]

Die Eigenschaft der perfekten Information kann im Allgemeinen nicht aus der Normalform eines Spiels ersehen werden. Innerhalb der Extensivform, die ein Spiel auf Basis eines gerichteten Graphen darstellt, wird die perfekte Information durch einelementige Informationsmengen charakterisiert.

Zufallsfreie endliche Spiele mit 2 Spielern ohne Unentschieden

Zermelos Satz gilt umso mehr für diejenigen unter den genannten Spielen, bei denen ein Unentschieden nicht vorkommen kann. Bei diesen endlichen Zwei-Personen-Nullsummenspielen mit perfekter Information ohne Zufallseinfluss und Unentschieden folgt aus seinem Satz die Aussage:

Eine Spielstellung gehört zu einer von genau zwei Kategorien:

Z-Stellung (von „Zwang“): Aus einer Z-Stellung muss immer eine C-Stellung gemacht werden.
C-Stellung (von „Chance“): Aus einer C-Stellung kann immer eine Z-Stellung gemacht werden.

Zermelos Argument ist allerdings ein mengentheoretisches Existenzargument und enthält keinen Algorithmus zur Kategorisierung der Stellungen eines bestimmten Spiels.

Wie oben erwähnt, liefert der Minimax-Algorithmus, der zu den graphentheoretischen Vorgehensweisen zu rechnen ist, zu jeder Stellung einen sie kategorisierenden Wert. Im Folgenden sollen jedoch weniger aufwändige Algorithmen und Kriterien vorgestellt werden.

Die Kategorisierung der Stellungen lässt sich bei kleinen Tableaus mit Bleistift und Papier erarbeiten, was der graphentheoretischen Kategorisierung entspricht. Hat man sich so einen ersten Eindruck verschafft, kann es gelingen, hieraus eine numerische Kategorisierung zu entwickeln.

Das Nim-Spiel (s. u.) wurde 1935 von Roland Sprague[5] und unabhängig davon 1939 von Patrick Michael Grundy[6] detailliert untersucht und zum Paradebeispiel dieser Art von Spielen gemacht (siehe auch Satz von Sprague-Grundy). Insofern markiert es einen Ausgangspunkt der mathematischen Spieltheorie.

Im genannten Papier von Grundy heißt die Z-Stellung «W» (für winning) und die C-Stellung «L» (für losing); bei Berlekamp « ${\mathcal {N}}$ -Position» (für negativ) bzw. « ${\mathcal {P}}$ -Position» (für positiv); bei Wythoff «kalt» bzw. «heiß». Es geht um die Kennzeichnung einer Stellung und nicht eines Zuges, was die Z- und C-Sprechweise am ehesten zum Ausdruck bringt.

Eins oder zwei

Dieses Streichholzspiel ist eines der einfachsten:

Zwischen zwei Spielern liegt ein Haufen Streichhölzer. Beide Spieler nehmen abwechselnd ein oder zwei Hölzchen. Wer das letzte Hölzchen nimmt, gewinnt (siehe Eins oder zwei und Bachet’sches Spiel).

Man kann die Regel auch abändern, indem derjenige verliert, der das letzte Hölzchen nehmen muss.

Wythoffs Spiel

Beim „Spiel von Wythoff“ (auch: „Wythoffs Nim“) entnehmen 2 Spieler abwechselnd von 2 Stapeln Gegenstände, und zwar von einem der beiden Stapel oder von beiden, dann aber gleich viele von jedem Stapel. Das Spiel endet, wenn ein Spieler den letzten Gegenstand entnimmt – womit er das Spiel gewinnt.

Das Spiel wurde von diesem niederländischen Mathematiker im Jahr 1907 mathematisch analysiert,[7] soll aber laut Martin Gardner in China unter dem Namen 捡石子 jiǎn shízǐ („Steine nehmen“) gespielt worden sein.[8]

Beim Spiel von Rufus Isaacs (zitiert aus Berge[9]) markieren die Spieler im I. Quadranten der Ebene mit ganzzahligem Gitter (in Formeln $\mathbb {N} _{0}\times \mathbb {N} _{0}$ ) abwechselnd einen Knoten, wobei sich der Nachfolgeknoten vom Vorgängerknoten aus gesehen auf einer gleichen Koordinate (waagerecht oder senkrecht) oder der Winkelhalbierenden jeweils in Richtung Ursprung befinden muss. Der Spieler, der als Erster den Ursprung erreicht, hat gewonnen. Die Anfangsstellung wird ausgelost.

Die beiden Spielregeln sind äquivalent. Allerdings eignet sich die graphische Auffassung besonders gut zur Darstellung des graphentheoretischen Algorithmus.

Nim

Beim Nim-Spiel sind mehrere Reihen mit Streichhölzern vorhanden. Zwei Spieler nehmen abwechselnd Streichhölzer aus einer der Reihen weg. Wie viele sie nehmen, spielt keine Rolle; es muss mindestens ein Streichholz sein und es dürfen bei einem Zug nur Streichhölzer einer einzigen Reihe genommen werden. Derjenige Spieler, der den letzten Zug macht – also die letzten Streichhölzer wegnimmt – gewinnt.

Misère-Nim

Der Spieler, der den letzten Zug macht (das letzte Streichholz nimmt), hat nicht gewonnen, sondern verloren. Diese Regel heißt Misère-Regel.

Das Nim-Spiel Marienbad, das durch den Film Letztes Jahr in Marienbad von Alain Resnais bekannt wurde, ist eine Misère-Variante.

Hex

Das strategische Brettspiel Hex ist ein nicht „neutrales“ (engl. impartial) Spiel, da die 2 Spieler, genannt „Rot“ und „Blau“, nur Züge mit Steinen ihrer Farbe machen können. Als Spiel dieses Typs kann es nicht mit dem Satz von Sprague-Grundy analysiert werden.

Für Spielregel etc. sei auf den

verwiesen. In diesem Artikel soll nur dargelegt werden, dass sich die Stellungen graphentheoretisch genauso kategorisieren lassen wie bei den anderen determinierten Spielen.

Graphentheoretische Kategorisierung

Die Stellungen lassen sich für jedes (endliche) Tableau in einem gerichteten Graphen darstellen mit Knoten für die Stellungen und Bögen (gerichteten Kanten) für die möglichen Züge. D. h. ein einzelner möglicher Zug wird durch einen Bogen repräsentiert, der von einer direkten Vorgänger-Stellung $u$ zu einer direkten Nachfolger-Stellung $v$ führt, in Zeichen $u\to v.$ Dieser Graph spiegelt die Spielregel eingeschränkt auf das Tableau genau wider.

Die eingangs aufgestellte Forderung nach Endlichkeit ist nur durch die Zyklenfreiheit des Graphen erfüllbar, der darum ein gerichteter azyklischer Graph (engl. DAG für directed acyclic graph) ist. In der so definierten Form werde er darum Stellungs-DAG genannt. Aus der Endlichkeit des Graphen selbst folgt, dass es Endknoten geben muss, also Knoten zu denen es keine Nachfolgeknoten gibt.

Ferner nehmen wir an:

Das Spiel soll zu Ende sein, wenn ein Spieler nicht mehr ziehen kann. Dieser soll dann auch der Verlierer sein.

Falls es einen Endknoten mit Misère-Gewinnregel gibt, fügen wir an ihn einen Bogen zu einem zusätzlichen Knoten hinzu, nach welch letztem Zug der nächste Spieler nicht mehr ziehen kann, somit der korrekte Verlierer ist.

Die Darlegung des nachfolgenden Algorithmus vereinfacht sich durch eine strenge Totalordnung $\succ$ der Stellungen, die mit der Zugfolge kompatibel ist. Sie kann bspw. wie folgt konstruiert werden:

Bei den genannten Spielen nimmt die Anzahl der Gegenstände im Tableau in jedem Zug entweder ab oder zu. Also nimmt man diese Anzahl als höchstrangiges Kriterium in einer lexikographischen Ordnung

\succ

. Nachrangige Kriterien müssen dafür sorgen, dass verschiedene Stellungen als größer resp. kleiner herauskommen, was immer möglich ist. Eine solche Totalordnung stellt sicher, dass aus

u\to v

immer

u\succ v

folgt.

Algorithmus[10]:

Wir beginnen beim Minimum der gewählten Totalordnung – es muss eine Senke und Endstellung sein. Wir arbeiten den Stellungsraum die Totalordnung aufsteigend (gegen die Richtung des Pfeils quasi „kausal rückwärts“) und schrittweise in Richtung ihres Maximums ab.

Kommen wir zu einem unmarkierten Knoten

v

, dann markieren wir ihn als Z-Knoten (=: Z-Aktion(

v

)). Danach markieren wir alle seine direkten Vorgänger

u

(also die

u\to v

) als C-Knoten (=: C-Aktion

(v,u)

).

Durch das schrittweise Vorgehen die Totalordnung „aufwärts“ ist sichergestellt, dass wir den ganzen Stellungsraum absuchen. Schon markierte Knoten bleiben ungeändert; es ist auch sonst keine Aktion bei ihnen erforderlich.

Beweis des Algorithmus und damit erneuter Beweis der Aussage:

Ist der Knoten

v

ein Z-Knoten, dann sind alle seine direkten Nachfolger

w

(also die mit

v\to w

) C-Knoten. Wäre nämlich ein Z-Knoten

w

dabei, hätte

v

als direkter Vorgänger von

w

von

w

aus in einer C-Aktion(

w,v

) als C-Knoten markiert werden müssen. Und unmarkiert kann ein Nachfolger

w

auch nicht sein, denn dann hätte eine Z-Aktion(

w

) wegen der „Zeitumkehr“ eigentlich vor der Z-Aktion(

v

) kommen müssen.

Seine direkten Vorgänger

u

(also die

u\to v

) können vor der C-Aktion(

v,u

) nur unmarkiert oder C-Knoten gewesen sein. Denn

u

kann nicht Z-Knoten sein, da wegen

u\succ v

die Z-Aktion(

v

) allemal vor einer Z-Aktion(

u

) geschähe.

In der graphentheoretischen Sprechweise haben wir zu einem gerichteten azyklischen Graphen einen Kern (engl. kernel, frz. noyau) konstruiert, d. i. eine stabile Untermenge von Knoten, die gleichzeitig dominierend ist. Der Kern ist die Menge der Z-Knoten. Er existiert immer[11] und ist eindeutig[12]. Die Stabilität steht für den Zwang, von einem Z-Knoten zu einem C-Knoten gehen zu müssen, und die Dominanz für die Chance, von einem C-Knoten zu einem Z-Knoten gehen zu können.

Der angeführte Algorithmus kann – zumindest theoretisch – von jeder Stellung klären, ob sie eine Gewinn- oder Verlustposition ist. Allerdings kann die Größe des Stellungs-DAG, der ja noch größer ist als der Stellungsraum, eine „praktische“ Implementierung unmöglich machen.

Die untenstehenden Graphiken stellen die Ergebnisse dar, die mit dem geschilderten Algorithmus gewonnen werden können. Dabei sind die von den (grünen) Z-Knoten ausgehenden C-Aktionen durch rote „Strahlen“ dargestellt, die die von ihnen getroffenen Knoten zu (roten) C-Knoten machen.

„Kern“ des Spiels von Wythoff

Eins oder zwei

Auch das triviale Spiel Eins oder zwei, dessen optimale Strategie ohne viel Mathematik sofort zu verstehen ist, lässt sich mit dem obigen Algorithmus behandeln: Der Stellungsraum ist ein Intervall $\left[0,n\right]$ von nicht-negativen ganzen Zahlen, die die augenblickliche Anzahl der Streichhölzer darstellen.

Wythoffs Spiel

Bei Wythoffs Spiel kommen die Eigenschaften des Kerns gut heraus. Die schwarze Skizze der Spielregel in der unteren rechten Ecke symbolisiert eine Art „Zukunftslichtkegel“, dem die „Vergangenheitslichtkegel“ entsprechen, die von den Z-Knoten (grün) ausgehen. Wird ein C-Knoten (rot) als Anfangsstellung ausgelost, kann der anziehende Spieler den Sieg erzwingen. Bei einem Z-Knoten (grün) als Anfangsstellung kann der Anziehende nur einen C-Knoten erreichen, wonach sein Gegenspieler den Sieg erzwingen kann.

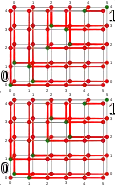
2 kolorierte Stellungsräume des Nim-Spiels mit 3 Reihen

Nim

Den Stellungs-DAG bettet man bei Nim in naheliegender Weise in das $n$ -dimensionale Intervall $\left[0,r_{1}\right]\times \left[0,r_{2}\right]\times \ldots \times \left[0,r_{n}\right]$ der Stellungen ein, wo $n$ die Anzahl der Reihen ist und $r_{i}$ die Anzahl der Streichhölzer in der $i$ -ten Reihe. Eine Spielstellung entspricht dann einem Knoten mit den momentanen Anzahlen von Streichhölzern als seinen Koordinaten. Die möglichen Züge (Bögen) sind parallel zu genau 1 Koordinate mit Richtung auf den Ursprung zu.

Eine jede der lexikographischen Ordnungen ist eine mit der Zugfolge kompatible Totalordnung. Es gibt nur eine Endstellung, welche mit dem Ursprung zusammenfällt.

Die Graphik rechts zeigt in 2 Diagrammen die Z-Stellungen (grüne Knoten) und die C-Stellungen (rote Knoten) für die Standard- (oben) und die Misère-Regel (unten) des Nim-Spiels – jeweils der Einfachheit halber in einem Tableau von 3 Reihen (Achsen) zu 5, 4 und 1 Hölzchen. In beiden Diagrammen ist die Reihe mit 1 Streichholz durch 2 übereinanderliegende Ebenen, die 0- und die 1-Ebene dargestellt, so dass die 0-Ebene effektiv dem Fehlen der dritten Reihe und die 1-Ebene dem Vorhandensein 1 Hölzchens in dieser Reihe entspricht.

Der Ursprung $(0,0,0)$ befindet sich jeweils links unten vorn.

Gültige Züge sind im Graphen Bewegungen auf genau einer der Koordinatenachsen, d. h. entweder waagerecht oder senkrecht oder auch in der dritten Richtung von der 1-Ebene auf die 0-Ebene, jeweils näher zum Ursprung hin.

Der Algorithmus beginnt am Ursprung, der bei der Standard-Regel grün, bei der Misère-Regel rot eingefärbt wird.

Es fällt auf, dass zwischen den 2 Nim-Varianten sich die Farben nur bei den Knoten ganz nahe am Ursprung unterscheiden.

Die Gewinnstrategie bei 2 Reihen für die Standard-Regel lautet: Wenn du kannst, ziehe mit deinem Gegenspieler gleich.

Bei 3 und mehr Reihen wird es komplizierter, wie schon die 1-Ebenen im Diagramm andeutungsweise zeigen. Die allgemeineren Fälle, insbesondere die mit mehr als 3 Reihen, sind noch schwieriger darzustellen.

Hex-Brett mit 11 mal 11 Feldern

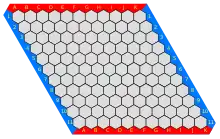
Hex

Besteht das rhombenförmige Brett aus $n$ mal $n$ sechseckigen Feldern, dann gibt es ${\binom {n^{2}}{{\big \lfloor }{\tfrac {n^{2}}{2}}{\big \rfloor }}}$ Endstellungen und gegen $3^{n^{2}}$ Stellungen insgesamt. Der geschilderte Algorithmus ist somit nur für sehr kleine $n$ praktikabel.

Als eine mit der Zugreihenfolge kompatible Totalordnung kann die lexikographische Ordnung von $(f,a_{1},\ldots ,a_{n^{2}})$ dienen mit $f\in \left[0,n^{2}\right]$ als Zahl der freien Felder in der höchsten lexikographischen Priorität, $i\in \left[1,n^{2}\right]$ als Index eines Feldes $F_{i}$ und

$a_{i}:={\begin{cases}\\\\\\\end{cases}}$	$0$ , falls $F_{i}$ frei,
	$1$ , falls $F_{i}$ rot,
	$2$ , falls $F_{i}$ blau,

bei der bspw. der Stellung (11² = 121, frei, frei, frei, …) die Stellung (120, rot, frei, frei, frei, …) und dieser die Stellung (119, rot, frei, blau, frei, frei, frei, …) folgen kann.

Im Stellungs-DAG alternieren die Züge an den roten Steinen mit denen an den blauen. Der Kern des Stellungs-DAG enthält Stellungen mit sowohl Rot wie Blau am Zug. Gut für Rot ist immer der erste Zug in die Mitte – aber er ist nicht der einzige gute. Schlecht ist der erste Zug in eine spitze Ecke, dann kann Blau mit seinem ersten Zug in die Mitte eine Z-Stellung erzeugen.

Minimax-Algorithmus

Minimax am Spiel Eins oder zwei
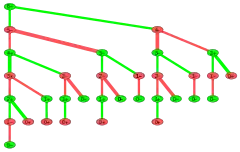
(Die dickeren Kanten sind die strategischen.)

Im Unterschied zum Stellungs-DAG des obigen Algorithmus benötigt der Minimax-Algorithmus einen Spielbaum, d. h. eine auf Wurzelbaum expandierte Version des Stellungs-DAG.

Eins oder zwei

Anhand des sehr einfachen Spiels Eins oder zwei sei der Minimax-Algorithmus erläutert.

In der nebensbleau des Spiels mit 6 Streichhölzern expandiert. Aus weiter unten angeführten Gründen seien die beiden Spieler „Maximierer“ und „Minimierer“ genannt. Die Ktehenden Abbildung ist der Spielbaum für ein Tanoten (Stellungen) und Kanten (Züge) sind grün für den Maximierer und rot für den Minimierer. Die Knoten enthalten eine Zahl und ein Vorzeichen: die Zahl ist die Anzahl der Streichhölzer und das Vorzeichen der Wert der Stellung mit der Bedeutung:

`+`	der Maximierer kann den Sieg erzwingen
`−`	der Minimierer kann den Sieg erzwingen

Der Algorithmus beginnt bei den Blättern des Baums, die alle für eine Endstellung von 0 Streichhölzern stehen. Da der Spieler, der am Zug wäre, verloren hat, erhält ein Blatt mit Maximierer am Zug die Markierung grün 0−, ein anderes rot 0+. Ein grüner Knoten erhält als Spielwert das Maximum der Spielwerte der Nachfolgeknoten bzw. ein roter Knoten deren Minimum; daher der Name Minimax und auch die Namen der Spieler. Sind die Werte der Nachfolgeknoten unterschiedlich, ist der strategisch optimale Zug verstärkt gezeichnet. Bei den Stellungen mit grün − und rot + ist es der den Zug abgebende Spieler, der den Sieg errungen hat oder erzwingen kann. (Es handelt sich um Z-Stellungen. Da der Minimax-Algorithmus immer zu einem Ergebnis kommt, ist schon durch seine Anwendbarkeit die Existenz und Eindeutigkeit eines Kerns des Stellungs-DAG bewiesen.)

Verglichen mit dem obigen Algorithmus ist der Minimax-Algorithmus etwas aufwändiger:

Er lässt beliebige reelle Spielwerte zu, auch wenn bei den zufallsfreien endlichen Spielen mit 2 Spielern ohne Unentschieden nur die 2 Werte + (:= +1) und − (:= −1) gebraucht werden.
Im Beispiel enthält der Spielbaum Wiederholungen, z. B. 8-mal die Stellung mit 1, 5-mal die mit 2, 3-mal die mit 3 und 2-mal die mit 4 Streichhölzern.
Die Knoten des Stellungs-DAG sind die Knoten in der Spalte ganz links. Sein Kern wird gebildet von den Knoten mit grün − und rot +.

Beide Algorithmen beginnen bei den Blättern und arbeiten sich zur Wurzel hoch, also entgegen der Richtung des Spiels.

Die anderen Spiele

Bei den anderen in diesem Artikel beschriebenen Spielen ergeben sich Einsparungen von Spielbaum zu Stellungs-DAG schon dadurch, dass es eine beliebig große Anzahl von Zügen gibt, die zur gleichen Stellung führen. Diese muss im Baum wiederholt werden, wogegen sie im DAG nur einmal vorkommt.
Darüber hinaus vereinfacht sich bei den Spielen Nim und Wythoffs Spiel der Stellungs-DAG dadurch, dass die Züge mit gemeinsamem Ziel in einer einfachen linearen Ordnung zueinander stehen.

Numerische Kategorisierung

Unter numerischer Kategorisierung soll verstanden werden, dass es eine Formel gibt, die für jede Stellung anhand ihrer numerisierten Parameter klärt, ob sie eine Gewinn- oder Verlustposition ist. Gibt es die Formel, dann darf in der Sprechweise des Artikels Gelöste Spiele das Spiel als „stark gelöst“ bezeichnet werden.

Eins oder zwei

Die Z-Knoten beim Spiel Eins oder zwei sind genau die Stellungen, bei denen die Anzahl der Streichhölzer durch 3 teilbar ist; bei der zugehörigen Misère-Regel ≡ 1 mod 3.

Wythoffs Spiel

Bei Wythoffs Spiel liegen die Z-Knoten auf den Koordinaten ${\big (}\lfloor n\Phi ^{2}\rfloor ,\lfloor n\Phi \rfloor {\big )}$ mit $n\geq 0$ und ${\displaystyle \Phi$ (Zahl des goldenen Schnitts) und dasselbe noch einmal an der Winkelhalbierenden gespiegelt.

Durch die Irrationalität von $\Phi \,$ ergibt sich eine aperiodische unregelmäßige Verteilung.

Nim

Bezgl. der Formeln für die Nim-Summen des Nim-Spiels und des Beweises ihrer Optimalität sei auf den Hauptartikel Nim-Spiel verwiesen. Die Z-Knoten des Graphen entsprechen Stellungen mit geraden Nim-Summen. Letztere kommen erst bei einer Anzahl ≥ 3 von Reihen, d. h. der Komposition mehrerer „Spiele“, richtig zum Tragen. In einer 2-dimensionalen Graphik ist das jedoch nur schwer deutlich zu machen.

Hex

Eine Strategie für Hex mit beliebig großem n×n-Tableau ist nicht bekannt. Es gibt aber Untersuchungen bis n≤10 zu gewissen Eröffnungszügen. Bei m×n-Tableaus mit m<n gibt es für den Spieler, der den kürzeren Weg hat, eine Gewinnstrategie (s. Hex).

Fazit

Der graphentheoretische Algorithmus bestimmt den „Spielwert“ einer Stellung. Im Sinne des Artikels Gelöste Spiele stellt er eine „schwache Lösung“ eines Spieles dar. Die Graphen sind naturgemäß stets endlich und damit zwar für den „Eigenbedarf“ des Spielers ggf. ausreichend. Die Expansion des Stellungsgraphen ist häufig von exponentieller Komplexität. Sie liefern auch Anhaltspunkte für die numerischen Formeln, die aber sehr unterschiedlich sein können. Von der mathematischen Warte aus sind die Formeln auf höheren Rängen anzusiedeln und bedürfen auch eines speziell auf sie zugeschnittenen Beweises. Sie sind – bei geeigneten Möglichkeiten der Auswertung – als „starke Lösungen“ anzusehen.

Offensichtlich ist es nicht interessant, eines dieser Spiele zu spielen, wenn beide Spieler die optimale Strategie kennen, da dann Sieger und Verlierer von vornherein feststehen. Beim Hex-Spiel ist diese allerdings nur für kleine n effektiv bekannt. Tatsächlich steht der Gewinner genau dann von vornherein fest, wenn einer der beiden Spieler die optimale Strategie spielt und an eine C-Stellung gerät.

Da bei einer vorliegenden C-Stellung die Z-Stellungen unter den Nachfolgestellungen eine verschwindende Minderheit darstellen, hat ein perfekter Spieler, der bei einer Z-Stellung beginnen – also seinem Gegenspieler eine C-Stellung überlassen – muss, umso größere Gewinnchancen je größer das Ausgangstableau ist und je mehr Fehlermöglichkeiten damit für den Gegenspieler bestehen. Und nach dem ersten Fehlgriff von dessen Seite ist er von der Straße des Sieges nicht mehr abzubringen.

Literatur

Claude Berge: Graphs et hypergraphes. Dunod, Paris 1970, Chapitre 14 Noyaux et fonctions de Grundy, S. 291–313 (französisch).
Jörg Bewersdorff: Glück, Logik und Bluff: Mathematik im Spiel – Methoden, Ergebnisse und Grenzen. Springer Spektrum, 6. Auflage, Wiesbaden 2012, ISBN 978-3-8348-1923-9, doi:10.1007/978-3-8348-2319-9_2, S. 95–245.
Elwyn Berlekamp, John Horton Conway, Richard K. Guy: Gewinnen, Braunschweig, 1985/86, 4 Bände, ISBN 3528085312, ISBN 3528085320, ISBN 3528085339, ISBN 3528085347 (engl. Original: Winning Ways for your Mathematical Plays., 2 Bände, ISBN 0120911019, ISBN 0120911027, aktualisierte Neuauflagen 2001 bis 2004).
G.H. Hardy, E. M. Wright: An introduction to the theory of numbers. Fifth edition. The Clarendon Press, Oxford University Press, New York, 1979, S. 117–120.

Einzelnachweise

Christian Rieck: Spieltheorie, Gabler, Wiesbaden 1993, ISBN 3-409-16801-X, S. 95.
Walter Schlee, Einführung in die Spieltheorie: mit Beispielen und Aufgaben, ISBN 3-528-03214-6, S. 95
E. Zermelo: Über eine Anwendung der Mengenlehre auf die Theorie des Schachspiels, Proceedings of the Fifth Congress of Mathematics, Vol. II, Cambridge 1913, S. 501–504 (Memento vom 24. März 2016 im Internet Archive)
H. W. Kuhn: Extensive games, Proceedings of the National Academy of Sciences of the USA, Band 36, 1950, S. 570–576 (online; PDF; 713 kB).
Roland P. Sprague: Über mathematische Kampfspiele, Tôhoku Mathematical Journal, 41 (1935), S. 438–444 (online).
Patrick M. Grundy: Mathematics and games, Eureka. 27 (1940), S. 9–11 (online (Memento des Originals vom 27. September 2007 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2).
W. A. Wythoff: A modification of the game of Nim, Nieuw Archief voor Wiskunde. Tweede reeks 7, 1907, S. 199–202
Wythoffs Spiel auf Cut-the-knot (zitiert das Buch von Martin Gardner Penrose Tiles to Trapdoor Ciphers)
Claude Berge, a. a. O., S. 308.
Claude Berge, a. a. O., S. 296.
Richardson (1953), s. Claude Berge, a. a. O., S. 299.
Claude Berge, a. a. O., S. 298.

Siehe auch

Nimm-ein-Quadrat-Spiel

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Christian Rieck: Spieltheorie, Gabler, Wiesbaden 1993, ISBN 3-409-16801-X, S. 95.

[2] Walter Schlee, Einführung in die Spieltheorie: mit Beispielen und Aufgaben, ISBN 3-528-03214-6, S. 95

[3] E. Zermelo: Über eine Anwendung der Mengenlehre auf die Theorie des Schachspiels, Proceedings of the Fifth Congress of Mathematics, Vol. II, Cambridge 1913, S. 501–504 (Memento vom 24. März 2016 im Internet Archive)

[4] H. W. Kuhn: Extensive games, Proceedings of the National Academy of Sciences of the USA, Band 36, 1950, S. 570–576 (online; PDF; 713 kB).

[Sprague-5] Roland P. Sprague: Über mathematische Kampfspiele, Tôhoku Mathematical Journal, 41 (1935), S. 438–444 (online).

[Grundy-6] Patrick M. Grundy: Mathematics and games, Eureka. 27 (1940), S. 9–11 (online (Memento des Originals vom 27. September 2007 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2).

[7] W. A. Wythoff: A modification of the game of Nim, Nieuw Archief voor Wiskunde. Tweede reeks 7, 1907, S. 199–202

[8] Wythoffs Spiel auf Cut-the-knot (zitiert das Buch von Martin Gardner Penrose Tiles to Trapdoor Ciphers)

[9] Claude Berge, a. a. O., S. 308.

[10] Claude Berge, a. a. O., S. 296.

[11] Richardson (1953), s. Claude Berge, a. a. O., S. 299.

[12] Claude Berge, a. a. O., S. 298.