Antoine-Augustin Cournot
Antoine-Augustin Cournot (* 28. August 1801 in Gray; † 31. März 1877 in Paris) war ein französischer Mathematiker und Wirtschaftstheoretiker. Er kann zur klassischen Ökonomie gezählt werden und gilt als Mitbegründer der mathematischen Wirtschaftstheorie.

Leben
Augustin Cournots mathematische Ausbildung erfolgte am Lycée de Besançon, seine Studien setzte er 1821 am École Normale zu Paris fort. Im Jahr 1834 wurde er Professor für Mathematik in Lyon. Seine Recherches sur les principes mathématiques de la théorie des richesses erschienen 1838, blieben zu dieser Zeit jedoch weitgehend unbeachtet. Er vereinfachte sie daher in den folgenden Jahren und veröffentlichte sie 1863 und 1876 erneut.
Einfluss auf die mathematische Wirtschaftstheorie
Der Name Cournot wird zumeist als erstes mit der Duopol-Theorie in Verbindung gebracht. Sein Name begegnet den meisten Studierenden der Ökonomie durch das Nash-Cournot-Gleichgewicht. Gelegentlich wird auch das Gewinnmaximum eines Monopols als Cournotscher Punkt bezeichnet. Er hatte aber an der Einführung der Anwendung der Mathematik auf die Wirtschaftswissenschaften maßgeblich Anteil. Viele seiner Ideen sind auch heute noch nahezu unverändert Teil der Mikroökonomie.
Aufbau
Die ersten drei Kapitel seiner Recherches nutzt Cournot, um „Reichtum“ zu definieren, absolute mit relativen Preisen zu vergleichen und festzulegen, dass für homogene Güter in einem gemeinsamen Markt nur ein einziger Preis gelten kann. Er definiert außerdem, dass alle handelnden Individuen einer Volkswirtschaft gewinnmaximierend handeln.
Kapitel 4 dient dazu, die von ihm im weiteren Verlauf verwendete Nachfragefunktion zu erklären. Beginnend mit der Analyse des Monopols in Kapitel 5 nähert sich Cournot seiner bekanntesten Untersuchung: Er betrachtet zunächst ein Gut, das nur von einem einzigen Produzenten hergestellt wird, erweitert das Modell in Kapitel 7 um einen beziehungsweise mehrere Wettbewerber und erreicht so seine berühmte Oligopol-Theorie, wobei der Spezialfall mit zwei Wettbewerbern, also das Duopol, graphisch wie analytisch eingehend beschrieben wird. Kapitel 8 schließt diese grundlegende Betrachtung durch die Einführung des vollständigen Wettbewerbs mit einer unendlich großen Anzahl von Wettbewerbern ab. Kapitel 6 behandelt die Einflüsse der Besteuerung eines Monopolisten.
Die übrigen vier Kapitel behandeln die „Kommunikation“ von Märkten, also den Handel zwischen verschiedenen Regionen, und die Auswirkungen auf das gesamte Volkseinkommen.
Untersuchung der Wettbewerbsformen
Zu beachten ist, dass die „Untersuchung der Wettbewerbsformen“ eigentlich eine Untersuchung des Preises von Gütern unter bestimmten Bedingungen ist. Cournot definiert einleitend Reichtum als Produkt aus Menge und Preis eines Gutes, wobei er eingesteht, dass dieser „Reichtum“ nicht unbedingt wohlfahrtsmaximierend ist. Als Beispiel führt er die Vernichtung von Gewürzen durch die holländische Ost-Indien-Gesellschaft an, die eine „tatsächliche Schaffung von Reichtum im kommerziellen Sinne des Wortes“ sei. Mit der später entwickelten Haushaltstheorie und damit besonders der Konsumentenrente ist es möglich, die negativen Folgen einer künstlichen Verknappung von Gütern eines Marktmacht besitzenden Anbieters für die allgemeine Wohlfahrt zu zeigen. Cournot jedoch blieb nichts anderes übrig, als eine intuitiv erfassbare Erklärung anhand von Beispielen zu wählen.
Das Gesetz der Nachfrage
Es ist davon auszugehen, dass Cournot Adam Smiths Wealth of Nations durchaus gründlich studiert hat. Smith zeigt im siebten Kapitel ein intuitives Verständnis der Eigenschaften einer Nachfragefunktion, ohne sie jedoch als solche zu bezeichnen oder gar genau zu definieren. Es war Cournot, der als Erster das Konzept einer vom Preis eines Gutes abhängigen Nachfrage in die Mathematik übertrug und sie als Funktion beschrieb.
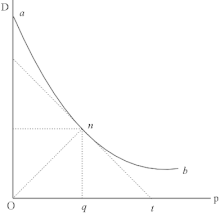
Cournout definiert die Nachfrage D als stetige und monoton fallende Funktion F(p), also als abhängig vom Preis p des jeweiligen Gutes.
An dieser Stelle sei darauf hingewiesen, dass sich Cournots Nachfragefunktion von der in der heutigen Mikroökonomie gebräuchlichen unterscheidet, da Cournot sie nicht aus einer Nutzenfunktion der Nachfrager herleitete. Zwar war er sich bewusst, dass das Gesetz der Nachfrage von dem Nutzen des Gutes abhängt, vertrat jedoch die Auffassung, dass die Gründe für die Nachfrage zu subjektiv und damit nicht in algebraischen Formeln auszudrücken seien. Er begründet die Eigenschaften der Nachfragefunktion daher ausschließlich durch empirische Beobachtungen, die einen negativen Zusammenhang zwischen Preis und Menge nahelegen. Die Erklärung des stetigen Verlaufes entspricht dagegen der heutigen: er gesteht ein, dass in einem kleinen Markt mit wenigen Nachfragern durchaus sprunghafte Veränderungen der Nachfrage auftreten können; sobald der Markt jedoch groß genug wird, sei die Annahme der Stetigkeit jedoch gerechtfertigt.
Welche Bedeutung diese Definition der Nachfrage hat, wird im weiteren Verlauf der Recherches deutlich. Durch die Darstellung der Nachfrage als Funktion gelingt es Cournot, seine Untersuchung der verschiedenen Marktformen in rigoroser, konsequenter Form aufzubauen.
Reaktionen und Einflüsse
Zu seinen Lebzeiten war Cournot zwar ein durchaus respektierter und anerkannter Wissenschaftler, seine Recherches jedoch wurden fast völlig ignoriert. Erst nach seinem Tod begannen sich seine Einflüsse auf die Entwicklung der Wirtschaftstheorie abzuzeichnen.
Was sich feststellen lässt, ist, dass die mathematische Behandlung des einfachen Monopol-Falles bis heute unverändert geblieben ist. Kaum ein Standard-Lehrbuch der Mikroökonomie verzichtet auf eine Wiederholung dieser Untersuchung, jedoch ohne dabei auf Cournot zu verweisen.
Des Weiteren scheint Cournot auf viele spätere Ökonomen, die mathematische Methoden anwendeten, einen großen Einfluss gehabt zu haben. So schreibt beispielsweise Walras 1874:
“I am indebted to my father, Auguste Walras, for the fundamental principles of my economic doctrine; and to Augustin Cournot for the idea of using the calculus of functions in the elaboration of this doctrine.”
und Marshall 1890:
“Cournot’s genius must give a new mental activity to everyone who passes through his hands.”
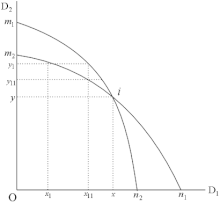
Eine der bekanntesten Untersuchungen der Cournotschen Duopoltheorie ist die 1883 erschienene Kritik des französischen Mathematikers Joseph Bertrand. Cournot ging bei seiner Herleitung des Gleichgewichts von der Menge der angebotenen Güter als entscheidender Variable aus, während Bertrand den Preis wählte. Im Falle zweier Anbieter mit gleicher Kostenstruktur, die um den Verkauf eines homogenen Gutes konkurrieren, kann einer der Wettbewerber seinen Preis minimal unter dem des anderen festlegen, woraufhin er die gesamte Nachfrage erhalten und somit seinen Gewinn erhöhen würde. Dies würde aber den anderen Anbieter dazu veranlassen, seinerseits den neuen Preis zu unterbieten – es wäre also ein Prozess in Gang gesetzt worden, der erst mit dem Erreichen der Grenzkosten enden würde.
Das Resultat dieses Wettbewerbs ist als Bertrand-Paradox bekannt: Obwohl es nur zwei Anbieter gibt, wird das Gut zu einem Preis verkauft, der dem des unbegrenzten Wettbewerbes entspricht. Heute bezeichnet man einen Wettbewerb nach Cournots Schema als Mengenwettbewerb, während der Bertrandsche Wettbewerb auch als Preiswettbewerb bekannt ist.
Das beschriebene Gleichgewicht im Duopol-Fall ist heute als Nash-Cournot-Gleichgewicht bekannt. Friedman vergleicht Cournots Leistung bei der Betrachtung des Duopols mit der von Adam Smith in Bezug auf die Nachfragefunktion: obgleich Smith eine vage Vorstellung über die Beschaffenheit einer Nachfragefunktion hatte, konnte er sie nicht exakt beschreiben, genauso wie Cournot eine vage Vorstellung über das spätere Nash-Gleichgewicht hatte, dieses aber nicht exakt beschreiben konnte.
Cournot behandelte seine Analyse der Situation so, als wäre sie eine dynamische, was allerdings falsch ist. Die große Beachtung, die diesem Aspekt seiner Untersuchung heute zuteilwird, beruht darauf, dass man diese Berechnung des Gleichgewichts auf statische Betrachtungen anwendet, wobei das offensichtliche nicht-kooperative Ergebnis dem von Cournot entspricht.
Literatur
- Joseph Bertrand: Théorie Mathématique de la Richesse Sociale. In: Journal des Savants, 1883
- Augustin Cournot: Untersuchungen über die mathematischen Grundlagen der Theorie des Reichtums, Jena 1924 (franz. Original: Recherches sur les principes mathématiques de la théorie des richesses, 1838)
- Augustin Cournot: Souvenirs 1760–1860 (Lebenserinnerungen von Cournot). 1859
- Irving Fisher: Cournot and Mathematical Economics. In: Quarterly Journal of Economics, 1898, S. 119–138
- James W. Friedman: An Experimental Study of Cooperative Duopoly. In: Econometrica, Vol. 35, 1967, No. 3/4, S. 379–397
- James W. Friedman: The Legacy of Augustin Cournot. University of North Carolina, Department of Economics, Working Paper, 1999, S. 99–05
- G. Granger: Cournot, Antoine-Augustin. In: Charles Coulston Gillispie (Hrsg.): Dictionary of Scientific Biography. Band 3: Pierre Cabanis – Heinrich von Dechen. Charles Scribner’s Sons, New York 1971, S. 450–454.
- Marco LiCalzi, Achille Basile: Economists and Mathematics from 1494 to 1969: Beyond the Art of Accounting. In: M. Emmer (Hrsg.): Matematica e Cultura 2000. Springer, Milano 2000, S. 95–107
- Thierry Martin: Bibliographie Cournotienne. In: ISIS, 90(3), 1999, S. 1045–1046
- Thierry Martin: La philosophie de l’histoire de Cournot. In: Revue d’Histoire des Sciences Humaines, Nr. 12, 2005/1, S. 141–162
- Robert Remak: Kann die Volkswirtschaftslehre eine exakte Wissenschaft werden? (1929) In: Martin J. Beckmann, Ryuzo Sato (Hrsg.): Mathematische Wirtschaftstheorie. Kiepenheuer & Witsch, Köln 1975, S. 16–27
- Léon Walras: Principe d’une théorie mathématique de l’échange. In: Journal des économistes, 1874
- Die kleine Encyklopädie. Encyclios-Verlag, Zürich, 1950, Band 1, S. 318
Weblinks
- Literatur von und über Antoine-Augustin Cournot im Katalog der Deutschen Nationalbibliothek
- Dirk Wigant: Antoine Augustin Cournot zum 200. Geburtstag: Leben und Werk. In: Ecochron.