Minimax-Algorithmus
Der Minimax-Algorithmus ist ein Algorithmus zur Ermittlung der optimalen Spielstrategie für endliche Zwei-Personen-Nullsummenspiele mit perfekter Information. Zu diesen Spielen gehören insbesondere Brettspiele wie Schach, Go, Othello / Reversi, Dame, Mühle und Vier gewinnt, bei denen beide Spieler stets die gesamte Historie der Partie kennen. Auch für Spiele mit Zufallseinfluss wie Backgammon lässt sich der Minimax-Algorithmus auf Grundlage von Erwartungswerten erweitern. In der Regel, aber nicht ausschließlich, wird der Minimax-Algorithmus auf Spiele mit abwechselndem Zugrecht angewandt.
Eine mit dem Minimax-Algorithmus berechnete Strategie wird Minimax-Strategie genannt. Sie sichert dem betreffenden Spieler den höchstmöglichen Gewinn, der unabhängig von der Spielweise des Gegners zu erzielen ist. Das aus den Minimax-Strategien beider Spieler gebildete Strategie-Paar bildet ein Nash-Gleichgewicht.
Bei Nicht-Nullsummenspielen, bei denen die Niederlage des Gegners nicht zwangsläufig mit dem eigenen Gewinn zusammenfällt, liefert der Minimax-Algorithmus nicht unbedingt eine optimale Strategie.
Varianten des Minimax-Algorithmus bilden das Kernelement von spielenden Programmen wie einem Schachprogramm. Die steigende Rechenleistung von Computern hat mittlerweile dazu geführt, dass selbst bei so komplexen Spielen wie Schach inzwischen alle Menschen ohne Mühe vom Computer geschlagen werden können.
Für einige Spiele wie das so genannte Nim-Spiel lässt sich eine optimale Strategie auch durch effizientere Algorithmen der Kombinatorischen Spieltheorie berechnen.
Bewertungsfunktion
Eine ideale Bewertungsfunktion ordnet einer Stellung den Wert +1 zu, wenn Spieler A gewinnt, und den Wert −1, wenn Spieler B gewinnt, und 0 bei Unentschieden. Kann man von sämtlichen Spielpositionen den Suchbaum bis zur maximalen Tiefe aufbauen (bis zur Endstellung, wo man sieht, wer gewinnt), so spielt der Algorithmus ein perfektes Spiel. Allerdings ist in der Praxis der vollständige Aufbau eines Suchbaums nur bei sehr einfachen Spielen wie Tic-Tac-Toe möglich.
Bei fast allen anderen Spielen ist dies zu rechenaufwendig. Deshalb begnügt man sich damit, den Suchbaum nur bis zu einer vorgegebenen Suchtiefe (Horizont) aufzubauen. Die Bewertungsfunktion wird modifiziert, sehr gute Spielpositionen für A erhalten sehr hohe Werte, sehr gute Spielpositionen für B erhalten sehr niedrige Werte. Zur Ermittlung der Werte bedient man sich Heuristiken zur Schätzung.
Suchbaum-Beispiel
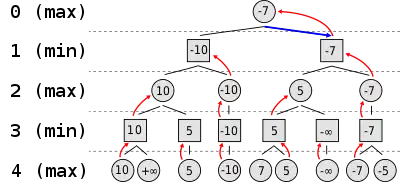
Das Bild rechts zeigt einen einfachen Baum mit Suchtiefe 4. Spieler A ist am Zug.
Die Knoten der Ebenen 0 und 2 entsprechen Spielsituationen, in denen Spieler A am Zug ist. Hier wird jeweils die Bewertungsfunktion der untergeordneten Knoten maximiert, d. h. der für Spieler A günstige Zug ausgewählt und dessen Wert dem Elternknoten zugewiesen.
Die Knoten der Ebenen 1 und 3 entsprechen Spielsituationen, in denen Spieler B am Zug ist. Hier wird jeweils die Bewertungsfunktion der untergeordneten Knoten minimiert, d. h. der für Spieler B günstigste Zug ausgewählt und dessen Wert dem Elternknoten zugewiesen.
Der Algorithmus beginnt unten bei den Blättern und geht dann nach oben bis zur Wurzel. In Ebene 3 wählt der Algorithmus den kleinsten Wert der Kindknoten und weist diesen dem Elternknoten zu (es wird minimiert). In Ebene 2 wird dann der jeweils größte Kindknoten dem Elternknoten zugewiesen (es wird maximiert). Dies wird abwechselnd so lange durchgeführt, bis die Wurzel erreicht ist. Der Wurzel wird der Wert des größten Kindknotens zugewiesen. Dabei handelt es sich dann um den Zug, der gespielt werden soll.
Anmerkungen
- Das Minimax-Verfahren ist im Kern vom speziellen Spiel unabhängig, das heißt zum Beispiel Schach und Reversi benutzen denselben Algorithmus.
- Schnittstellen zum speziellen Spiel sind lediglich die beiden folgenden Programmteile:
- Welche Züge sind in einer konkreten Spielsituation möglich?
- Wie wird eine Spielsituation numerisch bewertet?
- Neben dem Minimax-Verfahren kann ein Spiel weitere spielspezifische Verfahren anwenden, beispielsweise vorberechnete Bibliotheken für Eröffnungszüge.
Der Minimax-Algorithmus ist linear bezüglich der Anzahl der zu überprüfenden möglichen Züge. In der Regel benötigt man also mit steigender Suchtiefe exponentiell längere Zeit. (Man beachte, dass in der Theorie bei einem Spiel mit endlich vielen Zuständen die Laufzeit konstant ist, da ab einer gewissen Tiefe sich die Rechenzeit nicht mehr erhöht. Da bei den meisten Spielen diese Tiefe aber niemals realistisch erreicht werden kann, ist es durchaus berechtigt von einem exponentiellen Wachstum zu sprechen.) Andererseits steigt in der Regel (abhängig von der numerischen Bewertung) bei höherer Suchtiefe auch die Qualität des Suchergebnisses.
Es existieren daher verschiedene optimierte Varianten, zum Beispiel
- Variable Suchtiefe: Wenn nur noch wenige Zugmöglichkeiten pro Spielsituation existieren, etwa weil sich nur noch wenige Spielsteine auf dem Spielfeld befinden, kann die Suchtiefe erhöht werden (und umgekehrt).
- Dynamische Suchtiefe: Wenn sich die Zahlenwerte an einer Stelle des Suchbaums von Ebene zu Ebene stark ändern, kann die Suchtiefe lokal erhöht werden (und umgekehrt).
- Die Alpha-Beta-Suche kann verwendet werden.
Eine wesentliche Zeitersparnis ergibt sich durch Speicherung der bisher untersuchten Stellungen und deren Bewertungen. Wird eine Stellung durch verschiedene Zugfolgen von der Ausgangsstellung erreicht, braucht nicht jedes Mal wieder der gesamte darunter liegende Suchbaum durchsucht zu werden. In der Praxis verwendet man für diese Speicherung häufig effiziente Hashtabellen.
Iterative Tiefensuche
Speziell bei eingeschränkter Zeit für die Suche (z. B. im Turnierschach) wird iterative Tiefensuche (iterative deepening) verwendet. Dabei wird die Suche, ausgehend von der zu untersuchenden Stellung, wiederholt gestartet und dabei die gewünschte Suchtiefe schrittweise erhöht. Werden die bereits untersuchten Stellungen, wie oben beschrieben, gespeichert, müssen nur die gegenüber der vorhergehenden Suche neu erreichten Stellungen mit der Bewertungsfunktion bewertet werden. Dieses Verfahren wird so lange fortgesetzt, bis die verfügbare Suchzeit überschritten oder ein „hinreichend gutes“ Ergebnis erzielt wurde.
Ohne iterative Tiefensuche wäre beim Überschreiten des Zeitlimits im schlimmsten Fall nur ein einziger Zug untersucht worden, dieser aber bis in sehr große Tiefe. Der nächste Zug, der vielleicht schon nach nur einem einzigen Gegenzug den Gewinn gesichert hätte, wäre gar nicht erst ausprobiert worden.
Implementierung
Hauptprogramm (Auszug):
gespeicherterZug = NULL;
int gewuenschteTiefe = 4;
int bewertung = max(+1, gewuenschteTiefe);
if (gespeicherterZug == NULL)
es gab keine weiteren Zuege mehr;
else
gespeicherterZug ausführen;
Die normale Variante lautet:
int max(int spieler, int tiefe) {
if (tiefe == 0 or keineZuegeMehr(spieler))
return bewerten();
int maxWert = -unendlich;
generiereMoeglicheZuege(spieler);
while (noch Zug da) {
fuehreNaechstenZugAus();
int wert = min(-spieler, tiefe-1);
macheZugRueckgaengig();
if (wert > maxWert) {
maxWert = wert;
if (tiefe == gewuenschteTiefe)
gespeicherterZug = Zug;
}
}
return maxWert;
}
int min(int spieler, int tiefe) {
if (tiefe == 0 or keineZuegeMehr(spieler))
return bewerten();
int minWert = unendlich;
generiereMoeglicheZuege(spieler);
while (noch Zug da) {
fuehreNaechstenZugAus();
int wert = max(-spieler, tiefe-1);
macheZugRueckgaengig();
if (wert < minWert) {
minWert = wert;
}
}
return minWert;
}
Die NegaMax-Variante lautet:
int miniMax(int spieler, int tiefe) {
if (tiefe == 0 or keineZuegeMehr(spieler))
return bewerten(spieler);
int maxWert = -unendlich;
generiereMoeglicheZuege(spieler);
while (noch Zug da) {
fuehreNaechstenZugAus();
int wert = -miniMax(-spieler, tiefe-1);
macheZugRueckgaengig();
if (wert > maxWert) {
maxWert = wert;
if (tiefe == gewuenschteTiefe)
gespeicherterZug = Zug;
}
}
return maxWert;
}
Anmerkung: Während die Standard-Implementierung für einen Spieler maximiert und für den anderen Spieler minimiert, maximiert die Negamax-Variante für beide Spieler. Daraus folgt, dass sich die Bewertungsfunktion in beiden Implementierungen unterschiedlich verhalten muss.
- Standard-Implementierung: Je besser die Brettstellung für den maximierenden Spieler ist, desto größer ist der Rückgabewert der Bewertungsfunktion (Funktion bewerten()). Je besser sie für den minimierenden Spieler ist, desto kleiner ist der Rückgabewert.
- Negamax-Implementierung: Da beide Spieler maximieren, muss die Bewertungsfunktion umso größere Werte liefern, je besser die Brettposition des gerade Ziehenden ist (Funktion bewerten(spieler)). Der Wert wird immer aus dessen Sicht angegeben.
Variante: Der Negamax-Algorithmus
Um den Code zu vereinfachen und jeden Knoten des Suchbaumes gleich behandeln zu können, definiert man, dass jeder Spieler versucht, ein für sich selbst maximales Ergebnis, das heißt maximalen Wert der Bewertungsfunktion, zu erzielen. Dazu muss die Bewertung der Folgestellungen mit multipliziert werden (Negation, daher der Name). Damit muss nicht mehr unterschieden werden, ob A oder B am Zug ist und daher das Maximum oder das Minimum berechnet werden soll, sondern es wird in jeder Stellung immer nur das Maximum der negierten Bewertungen der Folgestellungen berechnet.
Siehe auch
- Minimax-Gleichgewicht als Spezialfall des Nash-Gleichgewichts
- Minimax-Regel
- Min-Max-Theorem
- Alpha-Beta-Suche – eine wesentliche Optimierung des Minimax-Algorithmus