Mechanismus-Design-Theorie

Die Mechanismus-Design-Theorie oder Mechanismen-Entwurf ist ein Teilgebiet der Spieltheorie, das Regeln – und damit die Anreize – für Spiele festlegt, um ein gewünschtes Gesamtergebnis zu erzielen, auch wenn die Spieler ausschließlich ihre eigenen Interessen verfolgen. Ein Mechanismus ist ein Satz von Regeln, um Interaktionen zwischen Spielern zu steuern.[1]

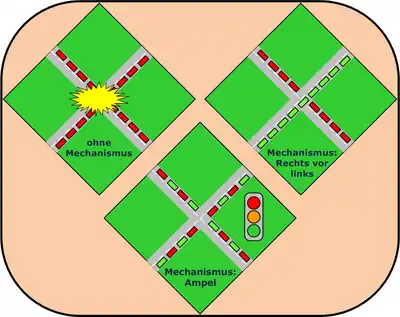
Die Darstellung zeigt schematisch ein Anwendungsbeispiel der Mechanismus-Design-Theorie auf die Verkehrsführung. Fehlen sämtliche Mechanismen, so führt das Streben nach Optimum der einzelnen Verkehrsteilnehmer zum Chaos. Der Mechanismus rechts vor links kann ebenfalls nur die Hälfte des maximal möglichen Gesamtergebnisses erzielen. Erst durch den Ampel-Mechanismus wird das in diesem Beispiel größt mögliche Gesamtergebnis erreicht.

Dies wird durch die Implementierung einer übergeordneten Struktur (Design) erreicht, in welcher die Spieler einen Anreiz dafür erhalten, dass sie sich diesen Regeln entsprechend verhalten. Das Resultat dieses Mechanismus wird als Implementierung des gewünschten Gesamtergebnisses bezeichnet. Die Stärke dieses Ergebnisses hängt von dem Lösungskonzept, also von den etablierten Regeln, ab. Es basiert auf der Metaspielanalyse, welche die Methode der Spieltheorie nutzt, um neue Regeln für ein Spiel zu entwickeln.

In der Mechanismus-Design-Theorie findet eine rekursive Anwendung der spieltheoretischen Analyse statt: Es wird nicht gefragt, wie die Spieler ein definiertes Spiel spielen werden, sondern wie ein Spiel gestaltet (designed, Design) werden muss, um ein bestimmtes Ergebnis zu erhalten.[2] Die im Spiel gestalteten Regeln werden als Mechanismus bezeichnet. Ein klassisches Anwendungsgebiet der Mechanismus-Design-Theorie ist die Gestaltung von Regeln in einem Markt.[3]

Theorie

Die Theorie geht davon aus, dass ein Markt nicht durch eine unsichtbare Hand für eine optimale Allokation der Ressourcen sorgt, sondern ein unvollkommener Markt vorherrscht. Mit Hilfe von Mechanismen soll ein nichtoptimaler Markt optimiert werden.

Die ökonomische Theorie weist auch nach, dass unter bestimmten Bedingungen wie vollständiger Wettbewerb, keine externen Effekte, keine einzelnen Spieler besitzen Marktmacht usw. die Regel ohne staatliche Eingriffe durch den Marktmechanismus implementiert werden kann. Der Marktmechanismus lässt sich in diesem Sinn als eine Form der Implementierung der Regel auffassen. Implementierung deckt sich in diesem Fall mit dem Wirken der unsichtbaren Hand.[4]

Das Prinzip des Mechanismusdesigns wirkt auch in anderen Lebensbereichen. So werden die Ergebnisse und Methoden des Mechanismen-Entwurfs auch im Bereich der Wirtschafts- und Sozialwissenschaften angewandt. Hierbei wird dann untersucht, wie die (meist) gesetzlichen Rahmenbedingungen so verändert werden können, dass ein bestimmtes, gewolltes Verhalten gefördert oder ein ungewolltes unterbunden wird.

Eine praktische Anwendung der Mechanismus-Design-Theorie ist die Frage, wie Beziehungen zu Geschäftspartnern gestaltet werden sollen, um die gewünschten Ergebnisse zu erzielen (die vereinbarten Regeln sind dann der „Mechanismus“, der entworfen werden soll). In der angewandten Spieltheorie wird diese Regelgestaltung populär als Coopetition bezeichnet.

Für ihre Forschung auf dem Gebiet wurden die Wissenschaftler Leonid Hurwicz, Eric S. Maskin und Roger B. Myerson im Jahr 2007 mit dem Nobelpreis für Wirtschaftswissenschaften ausgezeichnet.

Definition

$N$ stellt die Anzahl an Spielern dar. Jeder Spieler besitzt einen Wert $t_{i}\in T_{i}$ , der Typ des Spielers genannt wird. In einer Auktion beispielsweise würde dieser Wert den Reservationspreis dieses Spielers für die angebotene Ware(n) repräsentieren. Abhängig von seinem Typ wird der Spieler die Aktion $s_{i}(t_{i})\in A_{i}$ wählen, wobei $s_{i}(t_{i})\in A_{i}$ die vom Mechanismus ermöglichten Handlungsalternativen für den Spieler $i$ darstellt. Ein Beispiel für eine Aktion in einer geschlossenen Auktion wäre ein Gebot mit einem bestimmten Betrag. Jeder Spieler hat den Nutzen $u_{i}\colon T_{i}\times O\rightarrow {\mathbb {R} }$ , wobei $O$ die Menge der möglichen Ergebnisse des Mechanismus darstellt. In einer Auktion wäre das Ergebnis die abgeschlossene Allokation der Waren und die Zahlungen, die jeder Spieler tätigen muss. Der Nutzen für jeden Spieler wäre entsprechend der Reservationspreis der an ihn allozierten Waren, abzüglich des zu zahlenden Preises.

Demzufolge ist ein Mechanismus $M$ als Paar $(A,g)$ definiert, wobei $A=A_{1}\times \ldots \times A_{N}$ die Handlungsmöglichkeiten für die Spieler und $g\colon A\rightarrow O$ die Funktion darstellt, die die Handlungen des Spielers zum Ergebnis $o$ führen.

Direkte Mechanismen

Ein Mechanismus sei direkt, wenn die Handlungsmöglichkeiten gleich der Anzahl der Werte jedes Spielers sind, zum Beispiel $A_{i}=T_{i}$ für alle $i$ . Dies ist der Fall bei Auktionen, wo jedes Gebot der Spieler ihren Präferenzwert für das Produkt ankündigt. Allerdings besteht keine Notwendigkeit für eine tatsächliche Bewertung, wenn eine unterschiedliche Strategie einen besseren Nutzen erbringt. Dies führt zu dem Gedanken der direkten wahrheitsgemäßen Mechanismen.

Unter einem direkten Mechanismus wird also jedes beteiligte Individuum nach seiner privaten Information gefragt. Den Ankündigungen wird hierüber dann das Ergebnis einer sozialen Auswahlfunktion zugeordnet. Ein zentrales Ergebnis der Theorie des Mechanismus-Design ist, dass jede soziale Auswahlfunktion, die implementierbar ist, immer auch durch einen direkten Mechanismus erreicht werden kann. Dieses Ergebnis wird als Revelationsprinzip bezeichnet. Der direkte Mechanismus übernimmt sozusagen das Spielen der zum Typ des Spielers gehörenden gleichgewichtigen Strategie. Ist es unter dem indirekten Mechanismus optimal für einen Typ eine bestimmte Strategie zu spielen, so ist es unter dem direkten Mechanismus optimal den Typ wahrheitsgemäß zu annoncieren.[5] Ein konkretes Beispiel ist die Messung von Zahlungsbereitschaften. Zur Messung der Zahlungsbereitschaften kann man direkte Befragung durchführen, dieser direkte Mechanismus hat jedoch seine Grenzen, weil die direkte Befragung mit Validitäts- und Reliabilitätmängeln behaftet ist. In der Realität vergleicht der Käufer immer seinen Nutzen mit dem Preis, hier jedoch wird der Preis isoliert betrachtet.

Direkte wahrheitsgemäße Mechanismen

Ebenfalls bekannt als anreizkompatible Mechanismen. Ein Mechanismus sei direkt wahrheitsgemäß bezüglich eines gegebenen spieltheoretischen Lösungskonzepts, wenn für die Strategie $\!\ s_{i}(t_{i})=t_{i}$ , also die wahrheitsgemäße Enthüllung des eigenen Typs, gilt, dass sie Gleichgewichtsstrategie im gewählten Lösungskonzept ist. Der Vickrey-Clarke-Groves-Mechanismus beispielsweise ist direkt wahrheitsgemäß in dominanten Strategien.[6]

Dominante Strategien existieren nur für wenige Mechanismen. Häufig werden Mechanismus-Design-Probleme als Bayessche Spiele modelliert, in denen die Spielertypen durch zufällige Größen repräsentiert werden und das Ergebnis der Mechanismen im Bayesschen Nash-Gleichgewicht interessiert.

Anreizkompatible Mechanismen untersuchen, welche Regeln gesetzt werden müssen, damit beide Seiten in einer bestimmten Situation ein bestimmtes Verhalten zeigen. Im Kern steht der Zusammenhang zwischen dem Verhandlungsergebnis und den Angaben der Akteure über ihre jeweilige private Information.[7] Ein Beispiel für eine anreizkompatible Lösung zur Messung der Zahlungsbereitschaften wäre folgendes Szenario: Der Kaufinteressent gibt für ein Produkt zunächst seinen Preis an, den er bereit wäre zu zahlen. Anschließend wird ein zufälliger Preis gezogen. Liegt der Preis unterhalb der angegebenen Zahlungsbereitschaft, so muss der Interessent das Produkt zu dem gezogenen Preis kaufen, liegt der gezogene Preis darüber, besteht keine Kaufpflicht. In diesem Fall ist der Mechanismus anreizkompatibel, weil es im eigenen Interesse des Kaufinteressenten liegt, seine wahre Zahlungsbereitschaft preiszugeben.

Soziale Wahl

Eine Funktion $f\colon T_{1}\times \ldots \times T_{N}\rightarrow O$ wird soziale Auswahlfunktion genannt. Ein Mechanismus $M$ implementiert eine soziale Auswahlfunktion $f$ (bezüglich eines Lösungskonzeptes), wenn es ein Tupel $(s_{1},s_{2},\ldots ,s_{n})$ von Strategien mit folgenden Eigenschaften gibt:

das Tupel $(s_{1},s_{2},\ldots ,s_{n})$ stellt ein Gleichgewicht im gewählten Lösungskonzept dar, und
es gilt $g(s_{1}(t_{1}),\ldots ,s_{N}(t_{N}))=f(t_{1},\ldots ,t_{N})$ , das heißt, im Gleichgewicht gilt die Auswahlfunktion $f$ .

Offenbarungsprinzip

Wenn es einen Mechanismus gibt, der eine soziale Auswahlfunktion implementiert, dann gibt es ebenfalls einen direkt wahrheitsgemäßen (oder anreizkompatiblen) Mechanismus, welcher die gleiche Funktion implementiert.[6]

Beispiele

Basketball

Ein Beispiel für das Mechanismus-Design ist die Festlegung der Spielregeln für eine Sportart. Bei dem Basketballspiel muss die ballführende Mannschaft innerhalb von 24 Sekunden ihren Angriff abgeschlossen haben, ansonsten wechselt der Ballbesitz. Ein Unentschieden gibt es beim Basketball nicht. Ist der Punktestand nach Ablauf der regulären Spielzeit ausgeglichen, schließt sich eine Verlängerung von jeweils fünf Minuten an, bis ein Team mit mindestens einem Punkt Vorsprung gewonnen hat. Dieser Mechanismus führt die beiden Mannschaften beim Basketballspiel zu einem schnelleren und offensiveren Wettbewerb.

Aufteilung des Kuchens

Es gibt ein Stück Kuchen für zwei Kinder. Wie kann dieser Kuchen für die zwei Kinder aufgeteilt werden, damit die beiden Kinder zufrieden sind? Die Zufriedenheit der beiden Kinder gilt hier als das beabsichtigte Ergebnis, und der Verteilungsregel entspricht der Mechanismus, der in diesem Aufteilungsspiel durchgeführt werden soll. Ein guter Mechanismus lautet hier: Kind A soll das Kuchenstück in zwei Teile aufteilen, dann wird Kind B zunächst ein Teil davon auswählen, den andere Teil erhält Kind A. Somit kann man die Ungleichgewichte Verteilung des Kuchens von Kind A vermeiden.[8]

Vickreyauktion

Die Vickreyauktion ist ein Beispiel eines Mechanismus für Auktionen. Alle Bieter geben gleichzeitig verdeckte Gebote ab und der Bieter mit dem höchsten Gebot erhält das zu versteigernde Gut. Er muss jedoch nur den Preis des zweithöchsten Gebots zahlen. Die Regeln sind hier so gestaltet, dass es für jeden Bieter die beste Strategie ist, genauso viel zu bieten, wie ihm das Gut wert ist.

Literatur

Hans Peter Grüner; Wirtschaftspolitik Allokationstheoretische Grundlagen und politisch-ökonomische Analyse; S. 24–30; 3. Auflagen; 2007; Springer.
Manfred J. Holler; Gerhard Illing; Einführung in die Spieltheorie; S. 340–356; 5. Auflagen; 2003; Springer.
Bezalel Peleg; Peter Sudhöller; Introduction to the Theory of cooperative games; 2. Edition; 2007; Springer.
Steven J. Brams; Alan D. Taylor; The WIN/WIN Solution: Guaranteeing Fair Shares to Everybody; 1. Edition; 1999; New York.
Ingo Pies: Normative Institutionenökonomik. Zur Rationalisierung des politischen Liberalismus. J.C.B. Mohr (Paul Siebeck), Tübingen 1993.
Sebastian Pickerodt; Informationsgüterhandel mit Hilfe autonomer Agenten Gewinnmaximierung durch Preisdifferenzierung; S. 156–159; 1. Auflagen; 2006; Wiesbaden.

Weblinks

Einzelnachweise

vgl. Milgrom, Paul Robert: Putting Auction Theory to Work p. 21 (2004) Google Books
vgl. Dutta, Prajit K.: Strategies and Games p. 349 (1999) Google Books
vgl. Rieck, Christian: Professor Rieck's Spieltheorie-Seite@1@2Vorlage:Toter Link/www.spieltheorie.de (Seite nicht mehr abrufbar, Suche in Webarchiven) Info: Der Link wurde automatisch als defekt markiert. Bitte prüfe den Link gemäß Anleitung und entferne dann diesen Hinweis.
vgl. Manfred J. Holler & Gerhard Illing: Einführung in die Spieltheorie; S. 340–343; 5. Auflage; 2003; Springer
Vgl. Hans Peter Grüner, Grüner Wirtschaftspolitik Allokationstheoretische Grundlagen und politisch-ökonomische Analyse 3. Auflage S. 24 2007
See Archivierte Kopie (Memento des Originals vom 26. Dezember 2008 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2 for a proof.
Vgl. Archivierte Kopie (Memento vom 7. Februar 2009 im Internet Archive)
Vgl.S.T.Brams, A.D.Taylor; The Win-Win Solution; Guaranteeing Fair Shares To Everybody; Norton 1999

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] vgl. Milgrom, Paul Robert: Putting Auction Theory to Work p. 21 (2004) Google Books

[2] vgl. Dutta, Prajit K.: Strategies and Games p. 349 (1999) Google Books

[3] vgl. Rieck, Christian: Professor Rieck's Spieltheorie-Seite@1@2Vorlage:Toter Link/www.spieltheorie.de (Seite nicht mehr abrufbar, Suche in Webarchiven) Info: Der Link wurde automatisch als defekt markiert. Bitte prüfe den Link gemäß Anleitung und entferne dann diesen Hinweis.

[4] vgl. Manfred J. Holler & Gerhard Illing: Einführung in die Spieltheorie; S. 340–343; 5. Auflage; 2003; Springer

[5] Vgl. Hans Peter Grüner, Grüner Wirtschaftspolitik Allokationstheoretische Grundlagen und politisch-ökonomische Analyse 3. Auflage S. 24 2007

[proof-6] See Archivierte Kopie (Memento des Originals vom 26. Dezember 2008 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2 for a proof.

[7] Vgl. Archivierte Kopie (Memento vom 7. Februar 2009 im Internet Archive)

[8] Vgl.S.T.Brams, A.D.Taylor; The Win-Win Solution; Guaranteeing Fair Shares To Everybody; Norton 1999