Braess-Paradoxon

Das Braess-Paradoxon ist eine Veranschaulichung der Tatsache, dass eine zusätzliche Handlungsoption unter der Annahme rationaler Einzelentscheidungen zu einer Verschlechterung der Situation für alle führen kann. Das Paradoxon wurde 1968 von dem deutschen Mathematiker Dietrich Braess veröffentlicht.

Braess’ ursprüngliche Arbeit zeigt eine paradoxe Situation, in der der Bau einer zusätzlichen Straße (also eine Kapazitätserhöhung) dazu führt, dass sich bei gleichbleibendem Verkehrsaufkommen die Fahrtdauer für alle Autofahrer erhöht (d. h. die Kapazität des Netzes reduziert wird). Dabei wird von der Annahme ausgegangen, dass jeder Verkehrsteilnehmer seine Route so wählt, dass es für ihn keine andere Möglichkeit mit kürzerer Fahrtzeit gibt. Die Situation, die nach dem Bau der neuen Straße entsteht, kann in der Spieltheorie als Mehr-Personen-Gefangenendilemma interpretiert werden und so dieses Paradoxon erklären.

Gelegentlich wird das Paradox auch bei Selfish-Routern diskutiert. Darüber hinaus ist das Braess-Paradoxon ein Beispiel dafür, dass die rationale Optimierung von Einzelinteressen im Zusammenhang mit einem öffentlich bereitgestellten Gut zu einem für jeden Einzelnen verschlechterten Zustand führen kann.

Beispiel

Als Beispiel für das Auftreten des Braess-Paradoxons wird hier ein Straßennetz gewählt. Erweitert man dieses Straßennetz um eine weitere Straße, so verlängert sich für jeden Fahrer die Fahrzeit. Das Beispiel ist Braess’ Originalarbeit Über ein Paradoxon aus der Verkehrsplanung aus dem Jahr 1968 entnommen.

Ausgangssituation

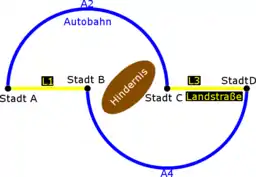
Bild 1: Skizze der Ausgangssituation

Bild 2: Verkehrsdichten bei 6000 Fahrern in der Stunde

Die vier Städte A, B, C und D sind durch vier Straßen verbunden. Sowohl von A nach C als auch von B nach D verläuft jeweils eine Autobahn. Die Autobahnen sind gut ausgebaut, so dass die Fahrtzeit nur wenig von der Verkehrsdichte abhängt. Allerdings müssen die Autobahnen ein Hindernis umwinden und sind deshalb recht lang. Bei einem Verkehrsaufkommen $x$ (in Tausend Autos pro Stunde) beträgt die entsprechende Fahrtzeit pro Fahrer

t_{\mathrm {AC} }(x)=t_{\mathrm {BD} }(x)=(50+x)\,\mathrm {min}

Die Städte A und B sind genauso wie die Städte C und D durch eine Landstraße verbunden. Diese Straßen sind zwar kürzer als die Autobahnen, aber dafür viel schlechter ausgebaut. Die Fahrtzeit pro Fahrer hängt deshalb im Wesentlichen nur vom Verkehrsaufkommen ab:

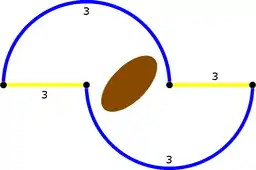
t_{\mathrm {AB} }(x)=t_{\mathrm {CD} }(x)=(0+10\cdot x)\,\mathrm {min}

Alle Autofahrer wollen von A nach D fahren, wobei jeder Fahrer den für ihn schnellsten Weg wählt. Es stellt sich ein sogenanntes Nash-Gleichgewicht ein, bei dem die Hälfte der Fahrer die Strecke über Stadt B benutzt und die andere Hälfte über Stadt C fährt. Bei stündlich 6000 Autofahrern fahren somit auf jeder Strecke 3000 Autos und alle Autofahrer haben eine Fahrtzeit von 83 Minuten.

Szenario nach dem Bau der zusätzlichen Straße

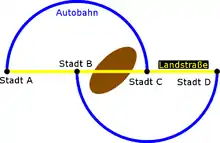
Bild 3: Skizze des Szenarios nach dem Bau der zusätzlichen Straße

Bild 4: Gleichgewichtssituation mit Neubaustrecke. Die Ströme (in 1000 Autos pro Stunde) sind an den Strecken angegeben

Die verantwortlichen Politiker entschließen sich nach einiger Zeit, wie in Bild 3 gezeigt einen Tunnel durch den Berg zwischen den Städten B und C zu bauen. Diese Neubaustrecke kann nur in der Richtung B → C befahren werden – das vereinfacht die Betrachtung, ist für das Auftreten des Paradoxons aber nicht relevant.

Auf dieser zusätzlichen Strecke gilt für die Fahrtdauer

t_{\mathrm {BC} }(x)=(10+x)\,\mathrm {min}

.

Diese Strecke ist also kurz und hat eine hohe Kapazität.

Auch hier gibt es ein Gleichgewicht (Bild 4), bei dem die Fahrtdauern auf allen Strecken gleich sind:

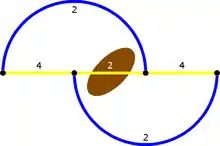
2000 Fahrer wählen die Strecke ABD
2000 Fahrer wählen die Strecke ACD
2000 Fahrer wählen die Strecke ABCD
Somit befindet sich auf den Landstraßen ein Strom von 4000 Fahrzeugen pro Stunde, auf den Autobahnen und der Neubaustrecke ein Strom von 2000 Fahrzeugen pro Stunde.

Die Fahrtdauer ist in diesem Fall für alle Fahrer gleich 92 Minuten und somit 9 Minuten länger als ohne die Neubaustrecke.

Veranschaulichung

Anschaulich betrachtet stellt sich jeweils für die Fahrer, welche eine der Autobahnen benutzen, ein zwangsläufig zu benutzender Landstraßenabschnitt als Nadelöhr dar. Dort hängt die Geschwindigkeit des Verkehrsflusses stark von der Anzahl der Straßennutzer ab bzw. wird durch diese verringert. Der Straßenneubau bewirkt nun aber, dass einige Fahrer die Landstraße auf voller Länge nutzen und diese somit zusätzlich verstopfen – sie benutzen zusätzlich zur Neubaustrecke nun beide Landstraßenabschnitte und nicht nur einen wie die Autobahnbenutzer. Nunmehr ist die Nadelöhrsituation deutlicher geworden, da auch die Autobahnbenutzer für ihren zwangsläufig genutzten Landstraßenabschnitt deutlich länger brauchen. In dem Beispiel kann die damit korrespondierende Verkehrsentlastung auf den kapazitätsstarken Autobahnen keinen ausgleichenden Zeitvorteil bewirken.

Diskussion

Man könnte nun vermuten, dass durch andere Routenwahlen einiger Fahrer eine bessere Situation entstünde. Dies ist jedoch nicht so. Ein Fahrer, der sich – sofern das geschilderte Gleichgewicht besteht – am nächsten Tag anders entscheidet, bewirkt durch seine Entscheidung, dass sich die Fahrtdauer auf der Strecke, für die er sich entscheidet – und damit für ihn selbst – verlängert. Dieser Zustand entspricht einem Nash-Gleichgewicht. Auf seiner Vortagesstrecke hingegen verringert sich die Fahrtdauer für alle anderen. Dies ist freilich kein Kriterium, das einen Fahrer zur Änderung seiner Route bewegt. Der Einfachheit halber ändern im folgenden Zahlenbeispiel jeweils 1000 Fahrer ihre Route gegenüber dem Gleichgewicht. Bei Änderung des Verhaltens eines einzelnen Fahrers wären die Änderungen kleiner, gingen jedoch – wegen der monotonen (linearen) Abhängigkeit der Fahrtdauer vom Fluss – immer in dieselbe Richtung.

Bild 5: Durchschnittliche Fahrtzeit, wenn von N=6000 Fahrern p über BD und k über BC fahren. D. h., N−p−k befahren AC, N−p CD, p+k AB, k BC, p BD. Das Minimum liegt bei p=3000, k=0 (roter Bereich).

3000 Fahrer wählen die Strecke ABD und benötigen 93 Minuten. 2000 Fahrer wählen die Strecke ACD und benötigen 82 Minuten. 1000 Fahrer wählen die Strecke ABCD und benötigen 81 Minuten.
3000 Fahrer wählen die Strecke ABD und benötigen 103 Minuten. 1000 Fahrer wählen die Strecke ACD und benötigen 81 Minuten. 2000 Fahrer wählen die Strecke ABCD und benötigen 92 Minuten.
2000 Fahrer wählen die Strecke ABD und benötigen 82 Minuten. 3000 Fahrer wählen die Strecke ACD und benötigen 93 Minuten. 1000 Fahrer wählen die Strecke ABCD und benötigen 81 Minuten.
1000 Fahrer wählen die Strecke ABD und benötigen 81 Minuten. 3000 Fahrer wählen die Strecke ACD und benötigen 103 Minuten. 2000 Fahrer wählen die Strecke ABCD und benötigen 92 Minuten.
1000 Fahrer wählen die Strecke ABD und benötigen 91 Minuten. 2000 Fahrer wählen die Strecke ACD und benötigen 102 Minuten. 3000 Fahrer wählen die Strecke ABCD und benötigen 103 Minuten.
2000 Fahrer wählen die Strecke ABD und benötigen 102 Minuten. 1000 Fahrer wählen die Strecke ACD und benötigen 91 Minuten. 3000 Fahrer wählen die Strecke ABCD und benötigen 103 Minuten.

Man beachte, dass auf allen Strecken mit 3000 Fahrern pro Stunde die Fahrtdauer länger als 92 Minuten ist.

Würden sich alle Fahrer verabreden, die Neubaustrecke zu ignorieren und sich so zu verhalten, wie sie es taten, als es diese noch nicht gab, wäre die Fahrtdauer für alle Verkehrsteilnehmer wieder 83 Minuten. Jedoch wäre die Versuchung groß, die dann freie Neubaustrecke als einziger doch zu nutzen und so die eigene Fahrtdauer von 83 Minuten auf 70 Minuten zu reduzieren. Die übliche menschliche Verhaltensweise ist dann, es den Vertragsbrüchigen gleichzutun. Das System tendiert somit wieder zum oben beschriebenen Gleichgewicht. Als Lösung dieses Dilemmas bleibt keine andere Möglichkeit, als die Neubaustrecke zentral geplant wieder abzureißen oder die Strecken AB und CD in ihrer Kapazität zu verdoppeln.

In seiner ursprünglichen Publikation klassifizierte Braess die Situation nicht als Gefangenendilemma, es ist aber eine Variante eines Mehr-Personen-Gefangenendilemmas mit drei Entscheidungsalternativen.[1]

Auftreten von Braess-Paradoxa in der realen Welt

Es gibt Beispiele, dass das Braess-Paradoxon nicht nur ein theoretisches Konstrukt ist. 1969 führte in Stuttgart die Eröffnung einer neuen Straße dazu, dass sich in der Umgebung des Schlossplatzes der Verkehrsfluss verschlechterte.[2] In New York konnte 1990 das umgekehrte Phänomen beobachtet werden. Eine Sperrung der 42. Straße sorgte für weniger Staus in der Umgebung.[3] Gleichermaßen verbesserten sich 2005 Verkehrsfluss und Fahrzeiten in der südkoreanischen Hauptstadt Seoul, nachdem eine vierspurige querungsfreie Stadtautobahn abgerissen worden war.[4][5] Weitere empirische Berichte über das Auftreten des Paradoxons gibt es von den Straßen Winnipegs.[6] In Neckarsulm verbesserte sich der Verkehrsfluss, nachdem ein oft geschlossener Bahnübergang ganz stillgelegt wurde. Die Wirkung zeigte sich, als er wegen einer Baustelle vorübergehend gesperrt werden musste. In Belgien führte die Stilllegung der Autobahn 601 zu einer verkehrlichen Verbesserung, weil es trotz des Umwegs über Kreuz Vottem durch den Wegfall von gefährlichen Ver- und Entflechtungsbereichen zu einem schnelleren Verkehrsfluss und deutlich weniger Unfällen kommt. Theoretische Überlegungen lassen darüber hinaus erwarten, dass das Braess-Paradoxon in Zufallsnetzen häufig auftritt.[7] Viele Netze der realen Welt sind Zufallsnetze.

Mechanisches Analogon

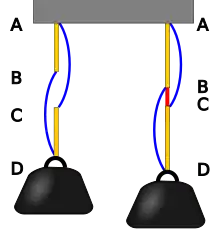
Mechanisches Analogon: Ein Gewicht hängt an zwei weichen Federn (gelb) und drei harten Federn (blau und rot)

Es gibt ein Analogon – wenn auch nicht im engen Sinne einer mathematischen Abbildbarkeit – zum Braess-Paradoxon in der Mechanik:[8]

Ein Gewicht (Gewichtskraft 6 N) ist an zwei Federsträngen aufgehängt. Der erste besteht oben aus einer schwachen gelben Feder (zwischen den Punkten A und B) und unten aus einer starken blauen Feder (zwischen B und D), der zweite Strang oben aus einer starken blauen Feder (zwischen A und C) und unten aus einer schwachen gelben Feder (zwischen C und D). Die gelben Federn haben in Abhängigkeit von der auf sie wirkenden Kraft $F$ die Länge $l_{\mathrm {g} }(F)=10\,\mathrm {\tfrac {cm}{N}} \cdot F$ , die blauen Federn die Länge $l_{\mathrm {b} }(F)=50\,\mathrm {cm} +1\,\mathrm {\tfrac {cm}{N}} \cdot F$ . Das Gewicht teilt sich gleichmäßig auf die Aufhängungen ABD und ACD auf, so dass auf beide Aufhängungen eine Kraft von 3 N wirkt. Die Länge der Federn beträgt dann

{\begin{matrix}l_{\mathrm {AB} }(3\,\mathrm {N} )=30\,\mathrm {cm} \\l_{\mathrm {BD} }(3\,\mathrm {N} )=53\,\mathrm {cm} \\l_{\mathrm {AC} }(3\,\mathrm {N} )=53\,\mathrm {cm} \\l_{\mathrm {CD} }(3\,\mathrm {N} )=30\,\mathrm {cm} \end{matrix}}

Die gesamte Aufhängung ist 83 cm lang.

Werden nun die Punkte B und C mit einer weiteren Feder (in der Skizze rot) verbunden, deren Länge $l_{\mathrm {r} }(F)=10\,\mathrm {cm} +1\,\mathrm {\tfrac {cm}{N}} \cdot F$ beträgt, könnte man vermuten, dass diese Feder einen Teil der Kraft aufnimmt und dadurch die anderen Federn entlastet, so dass sich das Gewicht hebt. Tatsächlich werden jedoch nur die blauen Federn entlastet und dafür die gelben Federn stärker belastet. Da die gelben Federn schwächer sind, werden sie stärker ausgedehnt als die blauen sich verkürzen. Dies führt dazu, dass sich das Gewicht senkt. Im Gleichgewichtszustand wirken auf die blauen Federn und die rote Feder Kräfte von je 2 N, auf die gelben Federn Kräfte von je 4 N, so dass sich folgende Längen ergeben:

{\begin{matrix}l_{\mathrm {AB} }(4\,\mathrm {N} )=40\,\mathrm {cm} \\l_{\mathrm {BD} }(2\,\mathrm {N} )=52\,\mathrm {cm} \\l_{\mathrm {AC} }(2\,\mathrm {N} )=52\,\mathrm {cm} \\l_{\mathrm {CD} }(4\,\mathrm {N} )=40\,\mathrm {cm} \\l_{\mathrm {BC} }(2\,\mathrm {N} )=12\,\mathrm {cm} \end{matrix}}

Die Länge der gesamten Aufhängung vergrößert sich damit auf 92 cm.

Anmerkung: Um das Gleichgewicht zu finden, muss folgendes Gleichungssystem für die Kräfte gelöst werden:

{\begin{matrix}F_{\mathrm {AB} }=F_{\mathrm {BD} }+F_{\mathrm {BC} }\\F_{\mathrm {CD} }=F_{\mathrm {BC} }+F_{\mathrm {AC} }\\F_{\mathrm {AB} }+F_{\mathrm {AC} }=6\,\mathrm {N} \\F_{\mathrm {AB} }=F_{\mathrm {CD} }\\l_{\mathrm {AB} }(F_{\mathrm {AB} })+l_{\mathrm {BC} }(F_{\mathrm {BC} })=l_{\mathrm {AC} }(F_{\mathrm {AC} })\end{matrix}}

Verwandtschaft mit anderen Problemen

Mit Hilfe des Braess-Paradoxons lässt sich eine Variante von Newcombs Problem lösen.[9]
Das Braess-Paradoxon ist eine Variante des Minderheiten-Spiels, wenn Minderheit so verstanden wird, dass ein Fahrer „gut fährt“, wenn er eine Straße wählt, die weniger befahren ist, als es die Gleichgewichts-Lösung vorsieht. Verallgemeinert man auf Kostenfunktionen, die nicht mehr monoton sind, trifft diese Aussage nicht mehr zu.
Das Braess-Paradoxon hat eine gewisse Ähnlichkeit mit dem Eisverkäufer-am-Strand-Problem. Dort wird ebenfalls eine Situation beschrieben, wie es theoretisch möglich ist, dass ein Systemoptimum verfehlt werden kann, wenn sich Handelnde weder absprechen noch zentral organisieren.

Siehe auch

Downs-Thomson-Paradoxon

Literatur

Dietrich Braess: Über ein Paradoxon aus der Verkehrsplanung. (PDF; 841 kB) In: Unternehmensforschung. 12, S. 258–268.
Katharina Belaga-Werbitzky: Das Paradoxon von Braess in erweiterten Wheatstone-Netzen mit M/M/1-Bedienern. ISBN 3-89959-123-2 (Dissertation).
Jörg Esser: Simulation von Stadtverkehr auf der Basis zellularer Automaten. Duisburg 1997, DNB 953736350, Kapitel 8 (Dissertation, Universität Duisburg).

Weblinks

Dietrich Braess’ Arbeitsseite mit Literaturverzeichnis zum Thema
Jane Hagstrom: Braess’s Paradox Examples – Single Origin-Destination Pair
Jane Hagstrom: Braess’s Paradox Examples – Multiple Origin-Destination Pairs

Einzelnachweise

Andreas Diekmann: Spieltheorie. Rowohlt Taschenbuch Verlag, Reinbek bei Hamburg 2009, ISBN 978-3-499-55701-9, S. 113–122.
Wolfgang Blum: Ewig lockt die Schnellstraße. In: Süddeutsche Zeitung. 24. Januar 2006.
G. Kolata: What if they closed 42nd Street and nobody noticed? In: New York Times. 25. Dezember 1990, S. 38.
J. Vidal: Heart and soul of the city In: The Guardian. 1. November 2006.
K. Schön: Stau? Reißt die Stadtautobahn ab! In: urbanist magazin. 7. Februar 2014.
C. Fisk, S. Pallotion: Empirical Evidence for Equilibrium Paradoxes With Implications for Optimal Planning Strategies. In: Transportation Research. Vol. 15A, 1981, no. 3, S. 245–248.
Greg Valiant, Tim Roughgarden: Braess’s paradox in large random graphs. In: Proceedings of the 7th ACM conference on Electronic commerce. Ann Arbor MI 2006.
Joel E. Cohen, Paul Horowitz: Paradoxical behaviour of mechanical and electrical networks. In: Nature. 352, 22. August 1991, S. 699–701, doi:10.1038/352699a0.
A. D. Irvine: How Braess’ Paradox Solves Newcomb’s Problem. In: International Studies in Philosophy of Science. Vol. 7, 1993, no. 2, S. 145–164.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Diekmann2009-1] Andreas Diekmann: Spieltheorie. Rowohlt Taschenbuch Verlag, Reinbek bei Hamburg 2009, ISBN 978-3-499-55701-9, S. 113–122.

[BLUM-2] Wolfgang Blum: Ewig lockt die Schnellstraße. In: Süddeutsche Zeitung. 24. Januar 2006.

[NYT-3] G. Kolata: What if they closed 42nd Street and nobody noticed? In: New York Times. 25. Dezember 1990, S. 38.

[Guardian-4] J. Vidal: Heart and soul of the city In: The Guardian. 1. November 2006.

[urbanist-5] K. Schön: Stau? Reißt die Stadtautobahn ab! In: urbanist magazin. 7. Februar 2014.

[Fisk-6] C. Fisk, S. Pallotion: Empirical Evidence for Equilibrium Paradoxes With Implications for Optimal Planning Strategies. In: Transportation Research. Vol. 15A, 1981, no. 3, S. 245–248.

[Valiant-7] Greg Valiant, Tim Roughgarden: Braess’s paradox in large random graphs. In: Proceedings of the 7th ACM conference on Electronic commerce. Ann Arbor MI 2006.

[8] Joel E. Cohen, Paul Horowitz: Paradoxical behaviour of mechanical and electrical networks. In: Nature. 352, 22. August 1991, S. 699–701, doi:10.1038/352699a0.

[Irvine-9] A. D. Irvine: How Braess’ Paradox Solves Newcomb’s Problem. In: International Studies in Philosophy of Science. Vol. 7, 1993, no. 2, S. 145–164.