Kombinatorische Spieltheorie

Kombinatorische Spieltheorie ist ein von John Horton Conway ca. 1970 begründeter Zweig der Mathematik, der sich mit einer speziellen Klasse von Zwei-Personen-Spielen befasst.

Die Eigenschaften dieser Spiele, die auch als kombinatorische Spiele bezeichnet werden, sind:

Kein Zufallseinfluss.
Es gibt keine für einen einzelnen Spieler verborgene Information (wie bei Spielkarten). d. h. es liegt perfekte Information vor.
Gezogen wird abwechselnd.
Es gewinnt derjenige Spieler, dem es gelingt, den letzten Zug zu machen (eine Ausnahme sind Misère-Versionen, bei denen der zuletzt ziehende Spieler verliert).
Jede Partie endet nach einer endlichen Zahl von Zügen.

Solche Spiele, zu denen Nim und (nach geringfügigen Regeltransformationen) Go und Schach gehören, eröffnen besonders dann interessante Möglichkeiten der mathematischen Analyse, wenn sie in Komponenten zerfallen, bei denen es keine gegenseitige Beeinflussung der Zugmöglichkeiten gibt. Beispiele sind Nim-Haufen und einige späte Endspielpositionen im Go; auch im Schach lassen sich einige Zugzwang-Positionen bei Bauernendspielen so deuten. Das Zusammensetzen von Positionen wird auch als Addition bezeichnet.

Die mathematische Bedeutung der kombinatorischen Spieltheorie resultiert daraus, dass die Spiele einer Unterklasse als Zahlen gedeutet werden können. Dabei lassen sich sowohl ganze als auch reelle und sogar transfinite (d. h. unendlich große und unendlich kleine) Zahlen konstruieren, deren Gesamtheit man auch surreale Zahlen nennt. Umgekehrt erscheinen die Spiele der kombinatorischen Spieltheorie als Verallgemeinerung der surrealen Zahlen.

Beispiel: Domineering

Das Spiel Domineering ist eines der Spiele, welche im Rahmen der kombinatorischen Spieltheorie behandelt werden können. Es soll zur Veranschaulichung dienen und konkrete Beispiele liefern.

Spielregeln

Beim Domineering legen zwei Spieler abwechselnd Dominosteine auf ein schachbrettartiges Spielfeld, wobei ein Stein genau zwei Felder abdeckt, die beim Setzen beide noch frei sein müssen. Wie in der kombinatorischen Spieltheorie allgemein üblich, werden die beiden Spieler als Links und Rechts bezeichnet. Der linke Spieler legt die in den folgenden Abbildungen blau dargestellten Dominosteine immer vertikal und der rechte Spieler seine rot dargestellten Steine immer horizontal auf das Brett. Wie bei allen Spielen der kombinatorischen Spieltheorie verliert derjenige Spieler das Spiel, der nicht mehr ziehen kann.

Will man eine Position analysieren, kommt es offensichtlich nur auf die Menge der noch freien Felder an, aber nicht, in welcher Weise die bereits belegten Felder bedeckt wurden.

Beispielpartie

Eine Partie auf einem 3×3-Brett könnte z. B. so verlaufen, wie es die nachfolgenden Abbildung zeigt: Links eröffnet durch Setzen des mit „1“ gekennzeichneten Steins. Rechts legt darauf den mit „2“ gekennzeichneten Stein, worauf Links durch Setzen des mit „3“ markierten Steins die Partie für sich entscheidet, weil Rechts dann keinen Platz mehr hat für einen horizontal zu setzenden, roten Stein.

A	B	C
D	E	F
G	H	I

→

2		3
D	1
G		I

Zur beispielhaft angeführten Partie bleibt noch anzumerken, dass Links in der mit dem dritten Zug erreichten Endposition sogar noch eine Zugmöglichkeit gehabt hätte. Außerdem kann die Menge der freien Felder, die alle weiteren Zugmöglichkeiten bestimmt, in Komponenten zerlegt werden, sofern diese Komponenten nicht über Seitenrändern von Feldern zusammenhängen. Zum Beispiel könnte bei der Endposition die Zerlegung

D

G

I

vorgenommen werden. Diese Möglichkeit der Zerlegung einer Position bzw. der umgekehrte Vorgang eines Nebeneinanderlegens von Positionen ist eine ganz wesentliche Eigenschaft kombinatorischer Spiele (siehe Summe von Spielen).

Mathematische Formalisierung

Für eine mathematische Modellierung wird jede innerhalb der kombinatorischen Spieltheorie mögliche Spielregel durch mathematische Objekte, nämlich insbesondere durch Mengen, beschrieben. Dazu sind für jede Position die Zugmöglichkeiten der beiden Spieler mathematisch formal zu charakterisieren.

Diese Charakterisierung der Zugmöglichkeiten konnte speziell beim Spiel Domineering für jede Positionen durch die Menge der noch freien Felder repräsentiert werden. Allgemein, d. h. für jedes beliebige kombinatorische Spiel, lassen sich die Zugmöglichkeiten einer Position durch zwei Mengen ${\mathcal {L}}$ und ${\mathcal {R}}$ charakterisieren, von denen jede jeweils die Positionen enthält, die der betreffende Spieler durch einen Zug erreichen kann. Im Sinne des mathematischen Modells wird dadurch jede Position zu einem kombinatorischen Spiel, das rekursiv durch diejenigen Spiele, die mit den durch einen Zug erreichbaren Positionen starten, definiert wird.

Allgemeine Schreibweise

Bei der Schreibweise hat sich die Notation von z. B. $\{L_{1},L_{2}\,|R_{1}\}$ für das Paar $(\{L_{1},L_{2}\},\{R_{1}\})$ eingebürgert, wenn der Spieler Links die beiden Zugmöglichkeiten nach $L_{1},L_{2}$ und Rechts nur die Zugmöglichkeit nach $R_{1}$ besitzt:

A
B
C	D

={\Bigg \{}



C	D

,

A

	D

{\Bigg |}

A
B

{\Bigg \}}

Ausgehend von dieser Schreibweise und der jeweiligen Identifikation einer Positionen mit dem Spiel, das von dieser Position startet, gelangt man zur folgenden Definition

Definition eines Spiels

Ein Spiel (im Sinne von Spielposition, engl. game) ist über folgende selbstreferentielle Konstruktion definiert:

Konstruktionsregel: Sind ${\mathcal {L}}$ und ${\mathcal {R}}$ zwei Mengen von Spielen, dann ist $\{{\mathcal {L}}|{\mathcal {R}}\}$ ein Spiel.

Die Mengen ${\mathcal {L}}=\{L_{1},L_{2},...\}$ und ${\mathcal {R}}=\{R_{1},R_{2},...\}$ werden auch die linken bzw. rechten Optionen des Spiels genannt und repräsentieren die Spielpositionen, die der linke bzw. rechte Spieler mit einem Zug aus der aktuellen Spielposition heraus erreichen kann.

Wie bereits für das Eingangsbeispiel erläutert, werden zur Verkürzung der Notation in der Regel die Optionen direkt aufgelistet und die Mengenklammern weggelassen:

\{{\mathcal {L}}|{\mathcal {R}}\}=\{L_{1},L_{2},...|R_{1},R_{2},...\}

Elementare Spiele

Das Fundament dieser rekursiven Definition bildet das Spiel 0, bei dem keiner der beiden Spieler mehr ziehen kann (die Menge der linken und rechten Optionen ist leer). Die entsprechende Position im Domineering ist das 1x1-„Brett“.

A

$0:=\{|\}$

In einem nächsten Schritt lassen sich nun weitere Spiele finden:

A

B

A

B

A	B
C

1:=\{0|\}

-1:=\{|0\}

*:=\{0|0\}

Gewinnklassen

In Bezug auf die mit guten Strategien sicher erzielbaren Gewinnaussichten gehört jede Position zu genau einer der folgenden vier Klassen:

Links kann bei optimaler Spielweise gewinnen, unabhängig davon, wer beginnt (Positiv)
Rechts kann das Spiel gewinnen, unabhängig davon, wer beginnt (Negativ)
Der den ersten Zug ausführende Spieler besitzt eine Gewinnstrategie (Fuzzy)
Der nachziehende Spieler besitzt eine Gewinnstrategie (Null)

		Links beginnt
		Links gewinnt	Rechts gewinnt
Rechts beginnt	Links gewinnt	Positiv (Links gewinnt immer)	Null (der Nachziehende gewinnt)
Rechts beginnt	Rechts gewinnt	Fuzzy (der Anziehende gewinnt)	Negativ (Rechts gewinnt immer)

Die bereits definierten elementaren Spiele können wie folgt klassifiziert werden: 1 ist positiv, −1 ist negativ, 0 ein Null-Spiel und * ist fuzzy.

Viele der untersuchten Spiele zerfallen im Laufe der Partie in unabhängige Einzelkomponenten (Endspiele im Go, Reihen beim Nim). Diese Teil-Spiele sind oft einfach genug, um vollständig analysiert zu werden. Daher ist eine zentrale Fragestellung der kombinatorischen Spieltheorie, wie sich die Gewinnaussichten des Gesamtspiels aus den Informationen zu den Teil-Spielen ableiten lassen. Die Temperaturtheorie liefert einen Algorithmus, mit dem man annähernd optimal spielen kann. Die maximale Abweichung von der theoretisch besten Strategie lässt sich dabei eingrenzen.

In einigen Fällen kann man bereits aus den Gewinnklassen Schlüsse ziehen:

Sind die beiden Komponenten eines Spiels positiv, so ist das gesamte Spiel positiv. Gleiches gilt für negative Spiele.
Null-Spiele haben die Eigenschaft, dass sie als Komponente keinen Einfluss auf den Ausgang des Spiels haben und die Gewinnklasse unverändert lassen. Zwei Spiele, die sich nur um ein Null-Spiel unterscheiden, werden daher als gleichwertig betrachtet.[Anmerkung 1]

Summe von Spielen

Die Summe zweier Spiele ist ein zentrales Konzept der kombinatorischen Spieltheorie, mit dem das vom Nim bekannte Nebeneinanderlegen von Positionen formalisiert und verallgemeinert wird: Eine Nim-Position besteht aus mehreren Haufen von Spielsteinen, und bei jedem Zug wird genau ein Haufen ausgewählt, wo der aktuelle Zug durchgeführt wird. Dabei hängen die Zugmöglichkeiten nur vom ausgewählten Haufen ab. Außerdem lässt jeder Zug die nicht ausgewählten Haufen unverändert.

Analog kann man zwei Spiele dadurch miteinander addieren, dass man sie nebeneinanderlegt und die Zugmöglichkeiten derart definiert, dass der ziehende Spieler einen der beiden Summanden auswählen muss, um dann dort einen zulässigen Zug auszuführen. Insbesondere besitzt ein Spieler, der in keinem der Summanden ziehen kann, keine Zugmöglichkeit mehr, so dass er verloren hat.

Formal ist die Summe der Spiele $G=\{L_{1},L_{2},...|R_{1},R_{2},...\}$ und ${\widehat {G}}=\{{\widehat {L}}_{1},{\widehat {L}}_{2},...|{\widehat {R}}_{1},{\widehat {R}}_{2},...\}$ rekursiv definiert als

G+{\widehat {G}}:=\{L_{1}+{\widehat {G}},L_{2}+{\widehat {G}},...,G+{\widehat {L}}_{1},G+{\widehat {L}}_{2},...|R_{1}+{\widehat {G}},R_{2}+{\widehat {G}},...,G+{\widehat {R}}_{1},G+{\widehat {R}}_{2},...\}

Vergleich zweier Spiele

Um zwei Spiele G und H miteinander vergleichen zu können, bestimmt man die Gewinnklasse des Differenzspiels $G-H=G+(-H)$ . Das Inverse $-H$ entspricht dabei einer Vertauschung der Rollen von Links und Rechts. Im Domineering kann dies durch ein Drehen des Brettes um 90 Grad erreicht werden. Formal ist

-\{L_{1},L_{2},...|R_{1},R_{2},...\}:=\{-R_{1},-R_{2},...|-L_{1},-L_{2},...\}

Auch diese Definition ist rekursiv.

Ist das Differenzspiel $G_{1}-G_{2}$ zweier Spiele $G_{1}$ und $G_{2}$ ein Null-Spiel, so hat für jedes Spiel $H$ die Summe $G_{1}+H$ dieselbe Gewinnklasse wie die Summe $G_{2}+H$ . Daher werden $G_{1}$ und $G_{2}$ als äquivalent angesehen. Unter Identifikation von Äquivalenzklasse und Vertreter schreibt man:

G_{1}=G_{2}

, falls

G_{1}-G_{2}

ein Null-Spiel ist.

Weiterhin wird definiert:

G>H

, falls

G-H

positiv ist.

G<H

, falls

G-H

negativ ist.

G\parallel H

, falls

G-H

fuzzy ist.

sowie

G\geq H

, falls

G>H

oder

G=H

G\leq H

, falls

G<H

oder

G=H

Entsprechend dieser Symbolik ist ein „größeres“ Spiel immer vorteilhaft für den linken Spieler.

Alternativ lassen sich die Ordnungsrelationen auch etwas formeller einführen, ohne Bezugnahme auf das nicht im Detail ausgeführte Konzept der optimalen Spielweise[Anmerkung 2].

Mit diesen Operatoren und Relationen erfüllen die Spiele (modulo Äquivalenz) die Eigenschaften einer kommutative Gruppe mit partieller Ordnung. Die Gesamtheit aller Spiele kann als echte Klasse jedoch genau genommen keine Gruppe sein, da die Definition einer Gruppe sich nur auf Mengen erstreckt. Wesentliche Beziehungen, welche sich im Fall von Mengen aus der Gruppeneigenschaft ableiten lassen, sind allerdings auch auf Klassen übertragbar.

Vereinfachung von Spielen und Normalform

Ein Spiel kann mit den folgenden zwei Regeln vereinfacht werden, ohne dass sich dabei der Wert des Spiels ändert (d. h. ohne die Äquivalenzklasse zu verlassen).

Dominierte Optionen

Sind in dem Spiel

\{L_{1},L_{2},L_{3},...|R_{1},R_{2},R_{3},...\}

zwei linke Optionen vergleichbar, z. B.

L_{1}\leq L_{2}

, so ist

L_{1}

eine durch

L_{2}

dominierte Option. Entsprechend ist eine rechte Option

R_{1}

durch

R_{2}

dominiert, falls

R_{1}\geq R_{2}

.

Dominierte Optionen können weggelassen werden, ohne den Wert eines Spiels zu verändern:

L_{1}\leq L_{2}\Rightarrow \{L_{1},L_{2},L_{3},...|R_{1},R_{2},R_{3},...\}=\{L_{2},L_{3},...|R_{1},R_{2},R_{3},...\}

R_{1}\geq R_{2}\Rightarrow \{L_{1},L_{2},L_{3},...|R_{1},R_{2},R_{3},...\}=\{L_{1},L_{2},L_{3},...|R_{2},R_{3},...\}

Anschaulich gesehen entspricht dies einer Spielsituation, in der ein Spieler eine Zugmöglichkeit hat, die eindeutig schlechter als ein alternativer Zug ist. Der Spieler wird unter keinen Umständen den schlechteren Zug wählen – somit spielt es für den Ausgang der Partie keine Rolle, ob der schlechte Zug überhaupt existiert oder nicht.

Umkehrbare Züge

In einem Spiel

G=\{L_{1},L_{2},L_{3},...|R_{1},R_{2},R_{3},...\}

wird der Zug des rechten Spielers nach

R_{1}

umkehrbar genannt, falls eine linke Option

R_{1}^{L}

von

R_{1}

existiert mit

R_{1}^{L}\geq G

. D.h.

R_{1}^{L}

ist für Links mindestens so gut wie die ursprüngliche Position. (Entsprechend ist ein Zug des linken Spielers nach

L_{1}

umkehrbar, falls eine rechte Option

L_{1}^{R}

von

L_{1}

existiert mit

L_{1}^{R}\leq G

.)

Für einen umkehrbaren Zug ändert sich der Wert des Spieles

G

nicht, wenn man annimmt, dass der Zug stets unmittelbar vom Gegenspieler beantwortet wird:

Ist in dem Spiel

\{L_{1},L_{2},L_{3},...|R_{1},R_{2},R_{3},...\}

die rechte Option

R_{1}

über

R_{1}^{L}=\{...|K_{1},K_{2},...\}

umkehrbar, so gilt

\{L_{1},L_{2},L_{3},...|R_{1},R_{2},R_{3},...\}=\{L_{1},L_{2},L_{3},...|K_{1},K_{2},...,R_{2},R_{3},...\}

.

Ist die linke Option

L_{1}

über

L_{1}^{R}=\{K_{1},K_{2},...|...\}

umkehrbar, so gilt

\{L_{1},L_{2},L_{3},...|R_{1},R_{2},R_{3},...\}=\{K_{1},K_{2},...,L_{2},L_{3},...|R_{1},R_{2},R_{3},...\}

.

Umkehrbare Spielzüge können durchaus sinnvoll sein. Der Spieler sollte nach der Umkehrung allerdings in dieser Teilposition weiterspielen, andernfalls wäre der Abtausch ein reiner Verlust.

Für endliche Spiele (solche, die insgesamt endlich viele Positionen enthalten) führt eine wiederholte Anwendung dieser zwei Regeln zur Normalform des Spiels, welche für jede Äquivalenzklasse eindeutig ist.

Im allgemeinen Fall lässt sich zumindest folgende Aussage machen: Haben zwei Spiele $G$ und $H$ weder dominierte Optionen, noch umkehrbare Züge, so folgt aus $G=H$ , dass $G$ und $H$ gleiche linke und rechte Optionen haben. D.h. für jede linke / rechte Option $A$ von $G$ gibt es eine linke / rechte Option $B$ von $H$ mit $A=B$ .

Beispiele für Spiele höherer Stufe

Mit vier Feldern lassen sich im Domineering Spiele der nächsten Stufe bilden:

A

B

C

D

={\Bigg \{}

A

D

,

C

D

{\Bigg |}\;{\Bigg \}}={\Bigg \{}

A

+

D

,

C

D

{\Bigg |}\;{\Bigg \}}=\{0+0,1|\}=\{0,1|\}=\{1|\}

(Die letzte Vereinfachung kann erfolgen, da $0\leq 1$ und $0$ damit eine dominierte Option ist.)

Andererseits ist auch

1+1=\{0|\}+\{0|\}=\{0+1,1+0|\}=\{1|\}

Man definiert

2:=\{1|\}

3:=\{2|\}

4:=\{3|\}

, usw.

d. h.

-2=\{|{-1}\}

-3=\{|{-2}\}

, usw.

Die Spiele $...,-2,-1,0,1,2,...$ lassen sich als eine Art Punktestand deuten: Der linke bzw. rechte Spieler hat nicht nur gewonnen, sondern könnte sogar noch eine gewisse Zahl weiterer Züge machen. Neben den ganzzahligen Spielen, gibt es auch solche, die als Punktestand ${\textstyle {\frac {1}{2}}}$ interpretiert werden können:

A
B
C	D

={\Bigg \{}



C	D

,

A

	D

{\Bigg |}

A
B

{\Bigg \}}={\Bigg \{}

C

D

,

A

+

D

{\Bigg |}

A

B

{\Bigg \}}=\{-1,0|1\}=\{0|1\}

Man definiert

\textstyle {\frac {1}{2}}:=\{0|1\}

.

Diese Zuordnung ist durch die folgenden Eigenschaften motiviert:

0<\textstyle {\frac {1}{2}}<1

\textstyle {\frac {1}{2}}+\textstyle {\frac {1}{2}}=1

,

wobei sich die zweite Beziehung wie folgt nachrechnen lässt:

\textstyle {\frac {1}{2}}-1=\{0|1\}+\{|0\}=\{-1|1-1,\textstyle {\frac {1}{2}}\}=\{-1|0,\textstyle {\frac {1}{2}}\}=\{-1|0\}=-\textstyle {\frac {1}{2}}

.

Des Weiteren gibt es aber auch Spiele, die sich nicht wie ein ausgespielter Punktestand verhalten. Sie sind „heiß“, in dem Sinne, dass jeder Spieler seine Situation verbessern kann, indem er in der entsprechenden Stellung zieht:

A
B	C
	D

={\Bigg \{}


	C
	D

{\Bigg |}

A

	D

{\Bigg \}}={\Bigg \{}

C

D

{\Bigg |}

A

+

D

{\Bigg \}}=\{1|0\}

Im Mittel hat $\{1|0\}$ denselben Wert wie $\textstyle {\frac {1}{2}}$ :

\{1|0\}+\{1|0\}=1

Im Unterschied zu $\textstyle {\frac {1}{2}}$ lässt sich $\{1|0\}$ jedoch nicht präzise einordnen, sondern ist fuzzy gegenüber Werten im abgesteckten Intervall:

\{1|0\}>-1,\quad \{1|0\}\parallel 0,\quad \{1|0\}\parallel \textstyle {\frac {1}{2}},\quad \quad \{1|0\}\parallel 1,\quad \{1|0\}<2

Auf dem Zahlenstrahl lässt sich $\{1|0\}$ daher nur unbestimmt in dem Bereich von 0 bis 1 verorten.

Surreale Zahlen

Unter den Spielen gibt es solche, welche mit reellen Zahlen identifiziert werden können, da sie derselben Arithmetik folgen. Genauer lassen sie sich die als surreale Zahlen bezeichneten Spiele wie folgt charakterisieren:

Eine surreale Zahl

n=\{l_{1},l_{2},...|r_{1},r_{2},...\}

ist ein Spiel, bei dem

alle linken und rechten Optionen surreale Zahlen sind
$l_{i}<r_{j}$ gilt, für jede linke Option $l_{i}$ und rechte Option $r_{j}$ .

Im Kontext der kombinatorischen Spieltheorie werden surreale Zahlen auch kurz als Zahl (engl. number) bezeichnet. Von den bereits definierten Spielen sind $...,-2,-1,0,1,2,...$ und $\textstyle {\frac {1}{2}}$ Zahlen, nicht jedoch $*$ und $\{1|0\}$ .

Zahlen zeichnen sich dadurch aus, dass sie total geordnet sind, d. h. für zwei Zahlen $x$ und $y$ gilt entweder $x<y$ , $x>y$ oder $x=y$ . Surreale Zahlen sind eine reichhaltige Klasse mit den Eigenschaften eines geordneten Körpers, welche nicht nur die ganzen, rationalen und reellen Zahlen enthält, sondern auch infinitesimale und infinite Vertreter hat. Genaueres dazu im Hauptartikel zu surrealen Zahlen.

Als Komponente in einer Spiel-Summe lassen sich Zahlen nach folgendem Satz sehr einfach Spiel-strategisch einordnen:

Zahl-Vermeidungs-Satz: Ist $n$ eine surreale Zahl und $G$ ein Spiel, aber keine surreale Zahl, so ist es im Summenspiel $n+G$ immer von Vorteil, im Spiel $G$ zu ziehen, sofern dies möglich ist.

D.h. in einem Spiel aus mehreren Komponenten ziehen die Spieler nur so lange in einer Komponente, bis eine Zahl (praktisch ein endgültiger Punktestand) erreicht ist. Am Ende wird abgerechnet, indem die verbleibenden Zahlen summiert werden: Ist die Summe positiv, so gewinnt Links, ist sie negativ gewinnt Rechts, ist sie 0, so gewinnt der nachziehende Spieler.

Eine unmittelbare Konsequenz des Satzes ist folgende Rechenregel:

Translationsprinzip: Ist $n$ eine Zahl und $G=\{L_{1},L_{2},...|R_{1},R_{2},...\}$ keine Zahl, so gilt; $\{L_{1},L_{2},...|R_{1},R_{2},...\}+n=\{L_{1}+n,L_{2}+n,...|R_{1}+n,R_{2}+n,...\}$ .

Hier wird vorausgesetzt, dass $G$ mindestens eine linke bzw. rechte Option besitzt. Dann folgt die Identität, da die restlichen Optionen der Summe nach dem Zahl-Vermeidungs-Satz dominiert sind.

Sonderfall: Neutrale Spiele

Kombinatorische Spiele, bei denen außer den dafür maßgeblichen Eigenschaften die Zugmöglichkeiten für beide Spieler stets identisch sind, heißen neutrale[1] Spiele (der englische Originalbegriff impartial wird z. T. auch mit objektiv[2] übersetzt). In Bezug auf die Gewinnaussichten gehört jede Position eines neutralen Spiels innerhalb der oben angeführten Gewinnklassen-Tabelle zu einer der beiden Klassen Fuzzy (der Anziehende hat eine Gewinnstrategie) oder Null (der nachziehende Spieler besitzt eine Gewinnstrategie).

Nim

Position des Nim-Spiels mit vier Haufen, die 1, 3, 5 und 7 Streichhölzer enthalten

Das bekannteste neutrale Spiel ist Nim. Gespielt wird es mit mehreren Haufen von Spielsteinen. In einem Zug müssen von genau einem Haufen beliebig viele Steine, mindestens aber ein Stein, entfernt werden.

Im Sinne der Kombinatorischen Spieltheorie entspricht jeder Nim-Position eine Summe von Spielen, die jeweils mit einem Haufen beginnen: Bezeichnet man, wie in der Kombinatorischen Spieltheorie üblich, mit $*n$ das Spiel, das mit einem aus $n$ Steinen bestehenden Haufen beginnt, dann entspricht die Nim-Position, die aus den Haufen der Größen $n_{1},\dots ,n_{k}$ besteht, dem Spiel $*n_{1}+\dots +*n_{k}$ .

Bereits 1901 veröffentlichte Charles Leonard Bouton[3] eine Gewinnstrategie für Nim, die auf einer expliziten Formel beruht, bei der die binär dargestellten Haufengrößen zu addieren sind. Dabei sollte man, sofern möglich, so ziehen, dass nach dem Zug die XOR-„Summe“ der binär dargestellten Haufengrößen gleich 0 ist. Zum Beispiel ist ein Zug zur Position, die aus den drei Haufen $5,4,1$ besteht, ein Gewinnzug, weil die XOR-Summe dieser drei Haufengrößen gleich 0 ist: $5+_{2}4+_{2}1=0$ , wobei das Symbol $+_{2}$ die XOR-Operation bezeichnet, die man auch als übertragslose Binäraddition auffassen kann.

Im Sinne der Äquivalenz von kombinatorischen Spielen entspricht Boutons Gewinnformel der Eigenschaft $*n+*m=*(n+_{2}m)$ . In Worten: Legt man zwei Haufen der Größen $n$ und $m$ zu einer neuen Position nebeneinander, dann ist die so entstehende Position äquivalent zu einer Position mit einem Haufen, der aus $n+_{2}m$ Steinen besteht. Das bedeutet: In jeder Position des Nim-Spiels und sogar in jeder Position eines kombinatorischen Spiels, in der die beiden Nim-Haufen mit $n$ und $m$ Steinen vorkommen, können die beiden Haufen durch einen einzigen Haufen mit $n+_{2}m$ Steinen ersetzt werden, ohne dass sich dadurch die Gewinnklasse, d. h. Null oder Fuzzy, ändert. Mit dieser Ersetzung wird die Komplexität einer Minimax-Analyse zum Finden eines optimalen Zuges entscheidend reduziert, da eine aus mehreren Haufen bestehende Nim-Position schrittweise auf einen einzigen Haufen reduziert werden kann:

*n_{1}+\dots +*n_{k}=*(n_{1}+_{2}\dots +_{2}n_{k})

Völlig formal, d. h. ohne jeden Bezug auf die verbal beschriebenen Nim-Spielregeln, lassen sich die Spiele der Form $*n$ innerhalb der Kombinatorischen Spieltheorie wie folgt definieren, wobei man die für beide Spieler identischen Optionen zur Vereinfachung nur einmal notiert:

*n=\{*(n-1),\dots ,*1,*0|*(n-1),\dots ,*1,*0\}=:\{*(n-1),\dots ,*1,*0\}

*0=\{|\}=0

Im Englischen wird für diese Spiele das aus den Begriffen numbers und nim gebildete Wortspiel nimbers als Bezeichnung verwendet, zum Teil als Nim-Zahlen ins Deutsche übersetzt.[4]

Nim-Varianten

Seit Bouton wurden viele Varianten des Nim vorgeschlagen, die wie Nim meist mit mehreren Haufen von Spielsteinen gespielt werden, für die aber die erlaubten Züge durch abweichende Spielregeln definiert werden. Die wohl älteste solche Variante wurde vom Schachweltmeister und Mathematiker Emanuel Lasker ersonnen und untersucht. Sie wird daher heute als Lasker-Nim bezeichnet. Bei diesem Spiel besteht ein Zug darin, entweder wie beim Standard-Nim beliebig viele Steinen von einem Haufen zu nehmen oder einen Haufen in zwei Haufen zu teilen, ohne dabei einen Stein zu entfernen.

Eine vollständige Analyse eines neutralen Spieles ist immer dadurch möglich, dass jeder Position eine äquivalente, aus nur einem Haufen bestehende Position des Standard-Nim zugeordnet wird. Diese Möglichkeit der Reduktion wurde unabhängig voneinander von 1935 von Roland Sprague[5] und 1940 von Patrick Michael Grundy[6] gefunden und wird daher auch als Satz von Sprague-Grundy bezeichnet. Ansätze der Reduktion hatte zuvor bereits der Schachweltmeister und Mathematiker Emanuel Lasker erörtert.[7][8]

Die Größe des Nim-Haufens, die einer Position $H$ eines neutralen Spiels zugeordnet ist, wird auch als dessen Grundy-Zahl $g(H)$ bezeichnet. Es gilt dann im Sinne einer Äquivalenz kombinatorischer Spiele:

H=*g(H)

Die Grundy-Zahl $g(H)$ eines neutralen Spiels $H=\{H_{1},\dots ,H_{k}\}$ kann relativ einfach rekursiv, d. h. aus den Grundy-Zahlen der in einem Zug erreichbaren Positionen $H_{1},\dots ,H_{k}$ , berechnet werden: Sie ist gleich der kleinsten natürlichen Zahl, die nicht Grundy-Zahl einer Nachfolgeposition ist, weswegen man auch von mex für minimum excluded spricht:

g(H)=min(\mathrm {N} -\{g(H_{1}),\dots ,g(H_{k})\})

Grundy-Zahlen besitzen die folgenden beiden Eigenschaften, die unmittelbar aus den entsprechenden Eigenschaften für das Standard-Nim hervorgehen:

Der anziehende Spieler verfügt genau dann über eine Gewinnstrategie, wenn die Grundy-Zahl ungleich 0 ist.
Die Grundy-Zahl einer Summe von Positionen ist gleich der XOR-Summe der Grundy-Zahlen der Summanden. Diese Eigenschaft reduziert maßgeblich die Komplexität der Analyse von Positionen, die aus mehreren Haufen zusammengesetzt sind.

Die beiden Eigenschaften erlauben es, für Nim-Varianten wie zum Beispiel das genannte Lasker-Nim einen Gewinnzug zu finden: Sucht man zum Beispiel für die Lasker-Nim-Position mit vier Haufen der Größen $1,3,5,8$ einen Gewinnzug, dann kann man dazu die Standard-Nim-Position mit den vier Haufen der Größen $g(1)=1,g(3)=4,g(5)=5,g(8)=7$ analysieren, für die der Zug zur Standard-Nim-Position $1,3,5,7$ ein Gewinnzug ist. Demgemäß sollte auch in der ursprünglichen Lasker-Nim-Position der zweite Haufen verändert werden, und zwar derart, dass eine Grundy-Zahl 3 entsteht. Möglich ist dies mit einer Teilung des zweiten Haufens, wodurch die Lasker-Nim-Position $1,{\underline {1,2}},5,8$ erreicht wird.[9]

Misère-Version des Nim

Bereits Bouton hatte auch die sogenannte Misère-Version des Standard-Nim gelöst, bei der abweichend von der üblichen Definition eines kombinatorischen Spiels der zuletzt ziehende Spieler verliert. Bouton fand, dass beim Standard-Nim die Fuzzy-Positionen, d. h. die dem Anziehenden eine Gewinnstrategie erlaubenden Positionen, zwischen Misère-Version und normaler Version weitgehend übereinstimmen. Die einzigen Ausnahmen sind die Positionen, die ausschließlich aus Haufen der Größe 1 bestehen. Bei ihnen kehrt sich das Gewinnverhalten um.[3]

Misère-Versionen anderer Nim-Varianten

Für andere Nim-Varianten sind die Misère-Versionen zum Teil deutlich schwieriger zu lösen. Eine Möglichkeit ergibt sich dadurch, dass der der Äquivalenz-Begriff von Spielen weniger eng gefasst wird. In diesem Sinn gelten zwei Positionen $G_{1}$ und $G_{2}$ der Misère-Version einer Nim-Variante bereits dann als äquivalent, wenn für jede Position $H$ dieser Nim-Variante (aber nicht unbedingt für jedes kombinatorische Spiel $H$ ) die beiden Positionen $G_{1}+H$ und $G_{2}+H$ stets den gleichen Gewinntyp, Fuzzy oder Null, aufweisen.

Zug des Kegel-Nims von

2,4,1

nach

2,1,1,1

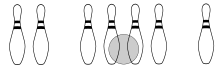
Auf Basis dieses Äquivalenzbegriffs lässt sich zum Beispiel die Misère-Version des Kegel-Nims (engl. Kayles) lösen: Beim Kegel-Nim müssen pro Zug von einem Haufen ein oder zwei Steine genommen werden, wobei der derart verkleinerte Haufen anschließend optional noch geteilt werden darf. Das Spiel verdankt seinen Namen der Sichtweise, bei der man sich eine Position als eine Reihe nebeneinander stehender, Lücken aufweisender Kegel vorstellen kann, bei denen pro Zug ein oder zwei Kegel, innerhalb oder am Rand einer Gruppe, herausgekegelt werden. Dabei entspricht der Fall, bei dem Kegel innerhalb einer Gruppe von Kegeln getroffen werden, dem Teil der Spielregel, bei dem die zuvor verkleinerte Gruppe von Kegeln geteilt wird.

Beim Kegel-Nim gibt es 40 Positionen, so dass jede Kegel-Nim-Position unter den Misère-Regeln äquivalent zu genau einer dieser Positionen ist. Daher kann die Analyse des Misère-Kegel-Nims darauf reduziert werden, für eine gegebene Position die zugehörige Äquivalenzklasse in Form einer äquivalenten Position unter diesen 40 Repräsentanten zu finden. Dies geschieht in zwei Schritten:[10][11]

Zunächst wird beschrieben, wie die Äquivalenzklassen addiert werden. Eine, wenn auch wenig elegante, Beschreibung erfolgt in Form einer 40×40-Tabelle. Diese Additionstabelle definiert für die Menge der Misère-Kegel-Nim-Äquivalenzklassen die Struktur einer abelschen Halbgruppe.
Außerdem muss für jede Position, die aus einem einzelnen Haufen besteht, die zugehörige Äquivalenzklasse bekannt sein. Beim Misère-Kegel-Nim ist für Ein-Haufen-Positionen die Zuordnung zu einer Äquivalenzklasse ab einer Haufengröße von 71 periodisch mit einer Periodenlänge von 12.

Erstmals gelöst, wenn auch auf einem anderen Weg, wurde die Misère-Version des Kegel-Nim im Jahr 1973. Eine Veröffentlichung erfolgte aber erst 1992. In Analogie zur Lösung der Misère-Version des Standard-Nims wurden die Kegel-Nim-Positionen charakterisiert, bei denen sich bei der Misère-Version ein anderer Gewinntyp ergibt als beim Kegel-Nim mit normaler Regel.[12]

Anwendung: Endspiele bei Go

Auch wenn Go eigentlich kein Spiel ist, bei dem der zuletzt ziehende Spieler gewinnt, so lassen sich doch Spiele im Sinne der kombinatorischen Spieltheorie konstruieren, welche die üblichen Go-Regeln nachbilden und effektiv zu demselben Spielresultat führen[13]. Am einfachsten lässt sich dies mit der historischen Steinbewertung realisieren, bei der beide Spieler das Brett mit Steinen vollsetzten (bis auf zwei Augen pro lebender Gruppe) und der Spieler mit den meisten Steinen auf dem Brett zum Sieger erklärt wird. Mit der Zusatzregel der Gefangenenrückgabe ist der Sieger zugleich auch die Person, welche zuletzt ziehen kann. Gefangenenrückgabe bedeutet, dass die Spieler nicht passen dürfen, aber anstelle eines regulären Zugs auch einen zuvor gefangenen Stein an den Gegner zurückgeben können (der Stein ist damit aus dem Spiel).

Die Steinbewertung unterscheidet sich von den heute weltweit üblichen Go-Regeln darin, dass auf jede Gruppe eine „Steuer“ von zwei Punkten erhoben wird. Aber auch die modernen Regel-Varianten lassen sich entsprechend abbilden.

Neben den Konventionen der klassischen kombinatorischen Spieltheorie nach John Conway gibt es allerdings auch alternative Formalismen, bei denen die Punktwertungen und deren Eigenschaften in Bezug auf die Komponenten einer (Endspiel-)Position direkt untersucht werden. Dies wird in den Arbeiten aus den 1950er Jahren von Milnor (1953)[14], Hanner (1959)[15] verfolgt, welche bereits wesentliche Ergebnisse der Temperaturtheorie enthalten, und von Berlekamp (1996)[16] weitergeführt.

In dem Buch Mathematical Go (1994) von Berlekamp und Wolfe werden die Ergebnisse der kombinatorischen Spieltheorie auf Endspiele im Go angewendet und die sich daraus ergebenen Spielstrategien herausgearbeitet. Es enthält Erkenntnisse und Leitlinien, welche zuvor nicht zum Wissenskanon von Profispielern gehörten und gilt als eine der wenigen Go-Publikationen von westlichen Autoren, welche im asiatischen Raum Beachtung fanden.

Anmerkungen

Beweis: Sei $N$ ein Nullspiel und $G$ ein Spiel, für das Spieler A eine Gewinnstrategie hat. Dieser Spieler hat dann auch für das zusammengesetzte Spiel $N+G$ eine Gewinnstrategie: Für jeden Zug, den der Gegenspieler in $N$ macht, antwortet Spieler A mit der Gewinnstrategie des Nachziehenden. Andernfalls zieht er in $G$ , entsprechend seiner Gewinnstrategie für $G$ .
Dazu wird definiert:
- $G\geq H:\Leftrightarrow$ keine rechte Option $G^{R}$ von $G$ existiert mit $H\geq G^{R}$ und keine linke Option $H^{L}$ von $H$ existiert mit $H^{L}\geq G$
sowie
- $G\leq H:\Leftrightarrow H\geq G$
- $G=H:\Leftrightarrow$ ( $G\leq H$ und $H\leq G$ )
- $G>H:\Leftrightarrow$ ( $G\geq H$ und nicht $G=H$ )
- $G<H:\Leftrightarrow H>G$
- $G\parallel H:\Leftrightarrow$ (weder $G\leq H$ noch $H\leq G$ )
Diese rekursive Definition ist mit dem Prinzip der optimalen Spielweise konsistent, denn für ein Spiel $G$ $\text{[math]}$ sind folgende Aussagen äquivalent:
- $G$ ist positiv oder null
- Wenn Rechts beginnt, so kann Links gewinnen
- Rechts hat keinen „gewinnenden Zug“
- Es gibt keine rechte Option $G^{R}$ von $G$ , für die gilt: Wenn Links beginnt, so kann Rechts gewinnen.
- Es gibt keine rechte Option $G^{R}$ von $G$ , die negativ oder null ist
D.h. symbolisch $G\geq 0\Leftrightarrow$ $\text{[math]}$ keine rechte Option $G^{R}$ $\text{[math]}$ von $G$ $\text{[math]}$ existiert mit $G^{R}\leq 0$ $\text{[math]}$ .

Siehe auch

Spieltheorie

Literatur

John Horton Conway: Über Zahlen und Spiele. Braunschweig, 1983, ISBN 3-528-08434-0, doi:10.1007/978-3-322-88997-3.
Elwyn R. Berlekamp, John H. Conway, Richard K. Guy: Gewinnen. Strategien für mathematische Spiele. Braunschweig, 1985/86, 4 Bände:
- Band 1, Von der Pike auf, ISBN 3-528-08531-2, doi:10.1007/978-3-322-83170-5;
- Band 2, Bäumchen-wechsle-dich, ISBN 3-528-08532-0, doi:10.1007/978-3-322-83171-2;
- Band 3, Fallstudien, ISBN 3-528-08533-9, doi:10.1007/978-3-322-83172-9;
- Band 4, Solitairspiele, ISBN 3-528-08534-7, doi:10.1007/978-3-322-83173-6.
Elwyn R. Berlekamp, David Wolfe: Mathematical Go, Chilling Gets the Last Point. 1994, ISBN 1-56881-032-6
Jörg Bewersdorff: Glück, Logik und Bluff: Mathematik im Spiel – Methoden, Ergebnisse und Grenzen, Springer Spektrum, 7. Auflage 2018, ISBN 978-3-658-21764-8, doi:10.1007/978-3-658-21765-5 (Kapitel 2.4 bis 2.9).
Aaron N. Siegel: Combinatorial Game Theory, Graduate Studies in Mathematics, Volume 146, American Mathematical Society 2013, ISBN 978-0-8218-5190-6, doi:10.1090/gsm/146
Richard J. Nowakowski: The History of Combinatorial Game Theory, Proceedings of the Board Game Studies Colloquium XI, Lissabon, 2008, online (Memento vom 31. Mai 2014 im Internet Archive)

Weblinks

Go und Mathematik

Einzelnachweise

Elwyn R. Berlekamp, John H. Conway, Richard K. Guy Gewinnen. Strategien für mathematische Spiele. Braunschweig, 1985, Band 1, ISBN 3-528-08531-2, S. 17, doi:10.1007/978-3-322-83170-5
John Horton Conway: Über Zahlen und Spiele. Braunschweig, 1983, ISBN 3-528-08434-0, S. 101, doi:10.1007/978-3-322-88997-3_12.
C. L. Bouton: Nim, a game with a complete mathematical theory, Annals of Mathematics, (2) 3 (1901), S. 35–39 (online bei JSTOR)
Elwyn R. Berlekamp, John H. Conway, Richard K. Guy: Gewinnen. Strategien für mathematische Spiele. Braunschweig, 1985, Band 1, ISBN 3-528-08531-2, doi:10.1007/978-3-322-83170-5. S. 43.
R. Sprague: Über mathematische Kampfspiele, Tôhoku Mathematical Journal, 41 (1935), S. 438–444 (Online-Version).
P. M. Grundy: Mathematics and games, Eureka. 27 (1940), S. 9–11 (Online-Version (Memento vom 27. September 2007 im Internet Archive)).
Emanuel Lasker: Brettspiele der Völker. Berlin 1931, S. 177 ff.
Auszugsweise zitiert in: Jörg Bewersdorff: Glück, Logik und Bluff: Mathematik im Spiel – Methoden, Ergebnisse und Grenzen, 7. Auflage, Wiesbaden 2018, S. 121–123, doi:10.1007/978-3-658-21765-5
Jörg Bewersdorff: Glück, Logik und Bluff: Mathematik im Spiel – Methoden, Ergebnisse und Grenzen, 7. Auflage, Wiesbaden 2018, S. 124–125, doi:10.1007/978-3-658-21765-5.
Jörg Bewersdorff: Glück, Logik und Bluff: Mathematik im Spiel – Methoden, Ergebnisse und Grenzen, 7. Auflage, Wiesbaden 2018, S. 175–177, doi:10.1007/978-3-658-21765-5.
Aaron N. Siegel, Combinatorial game theory, Providence, 2013, S. 251–252, doi:10.1090/gsm/146.
W. L. Sibert, J. H. Conway: Mathematical Kayles, International Journal of Game Theory, Band 20, 1992, S. 237–246, doi:10.1007/BF01253778.
Elwyn Berlekamp: Introductory overview of mathematical Go endgames, Combinatorial games, Lecture Notes AMS Short Course, Columbus/OH (USA) 1990, S. 73–100 (Abstract im Zentralblatt MATH)
John W. Milnor: Sums of positional games, Contrib. Theory of Games, II, Ann. Math. Stud., 28 (1953), S. 291–301, doi:10.1515/9781400881970-017 (Abstract im Zentralblatt MATH)
Olof Hanner: Mean play of sums of positional games, Pacific Journal of Mathematics, 9 (1959), S. 81–99 (Online-Version).
Elwyn Berlekamp: The economist's view of combinatorial games, Games of No Chance, 1996, S. 365–405 (Online-Version)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Beweis: Sei $N$ ein Nullspiel und $G$ ein Spiel, für das Spieler A eine Gewinnstrategie hat. Dieser Spieler hat dann auch für das zusammengesetzte Spiel $N+G$ eine Gewinnstrategie: Für jeden Zug, den der Gegenspieler in $N$ macht, antwortet Spieler A mit der Gewinnstrategie des Nachziehenden. Andernfalls zieht er in $G$ , entsprechend seiner Gewinnstrategie für $G$ .

[2] Dazu wird definiert:
$G\geq H:\Leftrightarrow$ keine rechte Option $G^{R}$ von $G$ existiert mit $H\geq G^{R}$ und keine linke Option $H^{L}$ von $H$ existiert mit $H^{L}\geq G$
sowie
$G\leq H:\Leftrightarrow H\geq G$

$G=H:\Leftrightarrow$ ( $G\leq H$ und $H\leq G$ )

$G>H:\Leftrightarrow$ ( $G\geq H$ und nicht $G=H$ )

$G<H:\Leftrightarrow H>G$

$G\parallel H:\Leftrightarrow$ (weder $G\leq H$ noch $H\leq G$ )
Diese rekursive Definition ist mit dem Prinzip der optimalen Spielweise konsistent, denn für ein Spiel $G$ sind folgende Aussagen äquivalent:
$G$ ist positiv oder null

Wenn Rechts beginnt, so kann Links gewinnen

Rechts hat keinen „gewinnenden Zug“

Es gibt keine rechte Option $G^{R}$ von $G$ , für die gilt: Wenn Links beginnt, so kann Rechts gewinnen.

Es gibt keine rechte Option $G^{R}$ von $G$ , die negativ oder null ist
D.h. symbolisch $G\geq 0\Leftrightarrow$ keine rechte Option $G^{R}$ von $G$ existiert mit $G^{R}\leq 0$ .

[3] $G\geq H:\Leftrightarrow$ keine rechte Option $G^{R}$ von $G$ existiert mit $H\geq G^{R}$ und keine linke Option $H^{L}$ von $H$ existiert mit $H^{L}\geq G$

[4] $G\leq H:\Leftrightarrow H\geq G$

[5] $G=H:\Leftrightarrow$ ( $G\leq H$ und $H\leq G$ )

[6] $G>H:\Leftrightarrow$ ( $G\geq H$ und nicht $G=H$ )

[7] $G<H:\Leftrightarrow H>G$

[8] $G\parallel H:\Leftrightarrow$ (weder $G\leq H$ noch $H\leq G$ )

[9] $G$ ist positiv oder null

[10] Wenn Rechts beginnt, so kann Links gewinnen

[11] Rechts hat keinen „gewinnenden Zug“

[12] Es gibt keine rechte Option $G^{R}$ von $G$ , für die gilt: Wenn Links beginnt, so kann Rechts gewinnen.

[13] Es gibt keine rechte Option $G^{R}$ von $G$ , die negativ oder null ist

[3] Elwyn R. Berlekamp, John H. Conway, Richard K. Guy Gewinnen. Strategien für mathematische Spiele. Braunschweig, 1985, Band 1, ISBN 3-528-08531-2, S. 17, doi:10.1007/978-3-322-83170-5

[4] John Horton Conway: Über Zahlen und Spiele. Braunschweig, 1983, ISBN 3-528-08434-0, S. 101, doi:10.1007/978-3-322-88997-3_12.

[bouton-5] C. L. Bouton: Nim, a game with a complete mathematical theory, Annals of Mathematics, (2) 3 (1901), S. 35–39 (online bei JSTOR)

[6] Elwyn R. Berlekamp, John H. Conway, Richard K. Guy: Gewinnen. Strategien für mathematische Spiele. Braunschweig, 1985, Band 1, ISBN 3-528-08531-2, doi:10.1007/978-3-322-83170-5. S. 43.

[7] R. Sprague: Über mathematische Kampfspiele, Tôhoku Mathematical Journal, 41 (1935), S. 438–444 (Online-Version).

[8] P. M. Grundy: Mathematics and games, Eureka. 27 (1940), S. 9–11 (Online-Version (Memento vom 27. September 2007 im Internet Archive)).

[9] Emanuel Lasker: Brettspiele der Völker. Berlin 1931, S. 177 ff.

[10] Auszugsweise zitiert in: Jörg Bewersdorff: Glück, Logik und Bluff: Mathematik im Spiel – Methoden, Ergebnisse und Grenzen, 7. Auflage, Wiesbaden 2018, S. 121–123, doi:10.1007/978-3-658-21765-5

[11] Jörg Bewersdorff: Glück, Logik und Bluff: Mathematik im Spiel – Methoden, Ergebnisse und Grenzen, 7. Auflage, Wiesbaden 2018, S. 124–125, doi:10.1007/978-3-658-21765-5.

[12] Jörg Bewersdorff: Glück, Logik und Bluff: Mathematik im Spiel – Methoden, Ergebnisse und Grenzen, 7. Auflage, Wiesbaden 2018, S. 175–177, doi:10.1007/978-3-658-21765-5.

[13] Aaron N. Siegel, Combinatorial game theory, Providence, 2013, S. 251–252, doi:10.1090/gsm/146.

[14] W. L. Sibert, J. H. Conway: Mathematical Kayles, International Journal of Game Theory, Band 20, 1992, S. 237–246, doi:10.1007/BF01253778.

[15] Elwyn Berlekamp: Introductory overview of mathematical Go endgames, Combinatorial games, Lecture Notes AMS Short Course, Columbus/OH (USA) 1990, S. 73–100 (Abstract im Zentralblatt MATH)

[16] John W. Milnor: Sums of positional games, Contrib. Theory of Games, II, Ann. Math. Stud., 28 (1953), S. 291–301, doi:10.1515/9781400881970-017 (Abstract im Zentralblatt MATH)

[17] Olof Hanner: Mean play of sums of positional games, Pacific Journal of Mathematics, 9 (1959), S. 81–99 (Online-Version).

[18] Elwyn Berlekamp: The economist's view of combinatorial games, Games of No Chance, 1996, S. 365–405 (Online-Version)