Pierpont-Primzahl
Eine Pierpont-Primzahl ist eine Primzahl der Form . Mit Hilfe der Pierpont-Primzahlen lässt sich angeben, welche regelmäßigen Polygone mit Zirkel und Lineal sowie einem Hilfsmittel zur Winkeldreiteilung konstruiert werden können. Sie sind nach dem US-amerikanischen Mathematiker James Pierpont benannt.
Definition
Eine Primzahl heißt Pierpont-Primzahl, wenn sie von der Form
ist, wobei natürliche Zahlen sind. Die Pierpont-Primzahlen sind damit diejenigen Primzahlen , für die 3-glatt ist.
Beispiele
Die ersten Pierpont-Primzahlen sind:
- 2, 3, 5, 7, 13, 17, 19, 37, 73, 97, 109, 163, 193, 257, 433, 487, 577, 769, 1153, 1297, 1459, 2593, 2917, 3457, 3889, … (Folge A005109 in OEIS)
Die derzeit größte bekannte Pierpont-Primzahl ist
mit 3.259.959 Dezimalstellen. Ihre Primalität wurde 2014 von Sai Yik Tang bewiesen.[1][2]
Eigenschaften
Spezialfälle
- Für und gibt es keine Pierpont-Primzahlen, denn ist eine gerade Zahl größer als zwei und damit zusammengesetzt.
- Für und muss eine Potenz von zwei sein und eine Pierpont-Primzahl ist damit eine fermatsche Primzahl.
- Für und hat eine Piermont-Primzahl die Form .
Verteilung
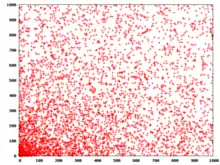
Die Anzahl der Pierpont-Primzahlen kleiner als ist
Die Anzahl der Pierpont-Primzahlen kleiner als ist
Andrew Gleason vermutete, dass es unendlich viele Pierpont-Primzahlen gibt.[3] Sie sind nicht besonders selten und haben wenige Einschränkungen bezüglich algebraischer Faktorisierungen. So gibt es beispielsweise keine Bedingungen, wie bei Mersenne-Primzahlen, dass der Exponent prim sein muss. Vermutlich gibt es
Pierpont-Primzahlen kleiner als , im Gegensatz zu Mersenne-Primzahlen im gleichen Bereich.
Faktoren von Fermat-Zahlen
Als Teil der laufenden weltweiten Suche nach Faktoren der Fermat-Zahlen, wurden bereits einige Pierpont-Primzahlen als Faktoren gefunden. Die folgende Tabelle[4] gibt Werte für , und an, sodass gilt:
- .
Die linke Seite ist eine Pierpont-Primzahl, falls eine Potenz von drei ist; die rechte Seite ist eine Fermat-Zahl.
| Jahr | Entdecker | |||
|---|---|---|---|---|
| 38 | 3 | 41 | 1903 | Cullen, Cunningham & Western |
| 63 | 9 | 67 | 1956 | Robinson |
| 207 | 3 | 209 | 1956 | Robinson |
| 452 | 27 | 455 | 1956 | Robinson |
| 9428 | 9 | 9431 | 1983 | Keller |
| 12185 | 81 | 12189 | 1993 | Dubner |
| 28281 | 81 | 28285 | 1996 | Taura |
| 157167 | 3 | 157169 | 1995 | Young |
| 213319 | 3 | 213321 | 1996 | Young |
| 303088 | 3 | 303093 | 1998 | Young |
| 382447 | 3 | 382449 | 1999 | Cosgrave & Gallot |
| 461076 | 9 | 461081 | 2003 | Nohara, Jobling, Woltman & Gallot |
| 495728 | 243 | 495732 | 2007 | Keiser, Jobling, Penné & others |
| 672005 | 27 | 672007 | 2005 | Cooper, Jobling, Woltman & Gallot |
| 2145351 | 3 | 2145353 | 2003 | Cosgrave, Jobling, Woltman & Gallot |
| 2478782 | 3 | 2478785 | 2003 | Cosgrave, Jobling, Woltman & Gallot |
| 2543548 | 9 | 2543551 | 2011 | Brown, Reynolds, Penné & Fougeron |
Anwendungen
Ein regelmäßiges Polygon mit Seiten kann genau dann mit Zirkel und Lineal sowie einem Hilfsmittel zur Winkeldreiteilung konstruiert werden, wenn von der Form
ist, wobei mit verschiedene Pierpont-Primzahlen größer als drei sind.[3][5] Die konstruierbaren Polygone, also die Polygone, die nur mit Zirkel und Lineal konstruiert werden können, sind hiervon Spezialfälle, bei denen und verschiedene Fermat-Primzahlen sind. Die kleinste Primzahl, die keine Pierpont-Primzahl ist, ist . Daher ist das Elfeck das kleinste regelmäßige Polygon, das nicht mit Zirkel, Lineal und Winkeldrittelung konstruiert werden kann. Alle anderen regelmäßigen -Ecke mit können mit Zirkel, Lineal und (gegebenenfalls) einem Hilfsmittel zur Winkeldreiteilung konstruiert werden.
In der Mathematik des Papierfaltens definieren die Huzita-Axiome sechs der sieben möglichen Faltungen. Diese Faltungen reichen ebenfalls aus, jedes regelmäßige Polygon mit Seiten zu bilden, wenn von der obigen Form ist.
Verallgemeinerung
Eine Pierpont-Primzahl der 2.Art ist eine Primzahl der Form . Die ersten Zahlen dieser Art sind:
- 2, 3, 5, 7, 11, 17, 23, 31, 47, 53, 71, 107, 127, 191, 383, 431, 647, 863, 971, 1151, 2591, 4373, 6143, 6911, 8191, 8747,… (Folge A005105 in OEIS)
Eine verallgemeinerte Pierpont-Primzahl ist eine Primzahl der Form mit k verschiedenen, immer größer werdenden geordneten Primzahlen .
Eine verallgemeinerte Pierpont-Primzahl der 2.Art ist eine Primzahl der Form mit k verschiedenen, immer größer werdenden geordneten Primzahlen .
In beiden Fällen muss sein. Alle weiteren sind ungerade Primzahlen.
Diese vorherige Aussage resultiert aus der folgenden Überlegung: Wäre p1 nicht 2, so wäre das Produkt aus ungeraden Primzahlpotenzen wieder ungerade. Wenn man dann noch 1 addiert oder subtrahiert, wäre die so erhaltene Zahl auf jeden Fall gerade und somit nicht prim.
Es folgen ein paar verallgemeinerte Pierpont-Primzahlen:
| {p1, p2, p3, …, pk} | +1 | OEIS-Folge | -1 | OEIS-Folge |
|---|---|---|---|---|
| {2} | 2, 3, 5, 17, 257, 65537 | (Folge A092506 in OEIS) | 3, 7, 31, 127, 8191, 131071, … | (Folge A000668 in OEIS) |
| {2, 3} | 2, 3, 5, 7, 13, 17, 19, 37, 73, 97, … | (Folge A005109 in OEIS) | 2, 3, 5, 7, 11, 17, 23, 31, 47, 53, … | (Folge A005105 in OEIS) |
| {2, 5} | 2, 3, 5, 11, 17, 41, 101, … | (Folge A077497 in OEIS) | 3, 7, 19, 31, 79, 127, 199, … | (Folge A077313 in OEIS) |
| {2, 3, 5} | 2, 3, 5, 7, 11, 13, 17, 19, 31, 37, 41, … | (Folge A002200 in OEIS) | ||
| {2, 7} | 2, 3, 5, 17, 29, 113, 197, … | (Folge A077498 in OEIS) | 3, 7, 13, 31, 97, 127, 223, … | (Folge A077314 in OEIS) |
| {2, 3, 5, 7} | 2, 3, 5, 7, 11, 13, 17, 19, 29, 31, 37, … | (Folge A174144 in OEIS) | ||
| {2, 11} | 2, 3, 5, 17, 23, 89, 257, 353, … | (Folge A077499 in OEIS) | 3, 7, 31, 43, 127, 241, 967, … | (Folge A077315 in OEIS) |
| {2, 13} | 2, 3, 5, 17, 53, 257, 677, … | (Folge A173236 in OEIS) | 3, 7, 31, 103, 127, 337, … | (Folge A173062 in OEIS) |
Weblinks
- Eric W. Weisstein: Pierpont Prime. In: MathWorld (englisch).
- Chris Caldwell: Pierpont prime. In: The Prime Pages. Abgerufen am 16. Mai 2013 (englisch).
Einzelnachweise
- Chris Caldwell: The largest known primes. In: The Prime Pages. 16. August 2016, abgerufen am 17. August 2016.
- Chris Caldwell: 3·210829346 + 1. In: The Prime Pages. 17. Januar 2014, abgerufen am 17. August 2016.
- Andrew Gleason: Angle Trisection, the Heptagon, and the Triskaidecagon. In: The American Mathematical Monthly. Band 95, Nr. 3, 1988, S. 185–194 (math.nthu.edu.tw [PDF]). math.nthu.edu.tw (Memento des Originals vom 2. Februar 2016 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.
- Wilfrid Keller: Prime factors of Fermat numbers and complete factoring status. (Nicht mehr online verfügbar.) 30. April 2015, archiviert vom Original am 10. Februar 2016; abgerufen am 17. August 2016. Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.
- Folge A048135 in OEIS