On-Line Encyclopedia of Integer Sequences
Die On-Line Encyclopedia of Integer Sequences (OEIS; deutsch Online-Enzyklopädie der Zahlenfolgen) ist eine englischsprachige Datenbank von Folgen ganzer Zahlen (integer sequences), die über das Internet durchsucht werden kann. Sie ist ein oft verwendetes Hilfsmittel und eine wichtige Quelle in der mathematischen Forschung.
Die Datenbank
Inhalt
Die Enzyklopädie ist eine Datenbank, in der Informationen über Folgen ganzer Zahlen gesammelt werden, die in der Mathematik von Interesse sind. Die Datenbank enthielt Mitte Februar 2022 über 351.000 Zahlenfolgen. Jeder Eintrag enthält eine Nummer, den Namen, die ersten Folgenglieder, Schlüsselworte, den Offset und den Autor, sowie optional Kommentare, Literaturangaben, Hyperlinks, eine Formel für die Zahlenfolge, Programme zur Erzeugung der Folge für Mathematica, Maple, PARI oder einer anderen Programmiersprache und Verweise auf verwandte Folgen, Erweiterungen der Folge und ihren Status.[1]
Die Datenbank enthält auch Ziffernfolgen der Darstellung von reellen Konstanten als Entwicklung nach Brüchen verschiedenen Basen, beispielsweise zur Basis 10 als A000796 und im Binärsystem als A004601.
Die Datenbank kann sowohl nach Schlüsselworten als auch nach Teilfolgen durchsucht werden. Es existierten Möglichkeiten zur akustischen und graphischen Darstellung von Zahlenfolgen.
Schlüsselworte
Es existieren u. a. folgende Schlüsselworte[2]:
- base: Die Folge hängt von einer Zahlenbasis ab, beispielsweise Quersummen oder Palindrome.
- cons: Dezimale Darstellung einer Zahl, z. B. für .
- core: Eine wichtige Zahlenfolge wie die Primzahlen oder die Fibonacci-Folge.
- hard: Die Ermittlung der Zahlenfolge ist schwierig.
- more: Die Erweiterung der Zahlenfolge ist wünschenswert (meist kombiniert mit hard)
- hear: Die eine hörenswerte Zahlenfolge. Hierzu bietet OEIS die Ausgabe als MIDI-Datei mit Beispielen an.
- look: Die Darstellung dieser Zahlenfolge ist ästhetisch ansprechend. Zwei Beispiele aus mehreren Tausend sind A331124 und A347347.
Quellen
Prinzipiell kann jeder zu der Datenbank beitragen. Zur Qualitätssicherung existiert ein mehrstufiges Prüfungsverfahren.[3]
Internes Format
Die Folgen werden in der Datenbank in einem reinen ASCII-Zeilenformat beschrieben. Jede Zeile beginnt mit einem Prozentzeichen, einem Buchstabencode für den Typ der Teilinformation, der Nummer der Folge und der jeweiligen Teilinformation. Folge A004002 ist zum Beispiel so gespeichert:
%I M3010
%S 1,3,15,3814279
%N Benford numbers: a(n)=e^e^...^e (n times) rounded to nearest integer.
%C The next term, a(4) ~ 2.3315*10^1656520, has 1656521 decimal digits and is therefore too large to be included. [Rephrased by _M. F. Hasler_, May 01 2013]
%D N. J. A. Sloane and Simon Plouffe, The Encyclopedia of Integer Sequences, Academic Press, 1995 (includes this sequence).
%D P. R. Turner, Will the "real" real arithmetic please stand up?, Notices Amer. Math. Soc., 38 (1991), 298–304.
%F a(n) = round(e^e^...^e), where e occurs n times, a(0) = 1 (= e^0). - _Melissa O'Neill_, Jul 04 2015
%t Round[NestList[Power[E, #] &, 1, 3]] (* _Melissa O'Neill_, Jul 04 2015 *)
%Y Cf. A056072, A225053.
%Y Cf. A073236. - _Melissa O’Neill_, Jul 04 2015
%K nonn
%O 0,2
%A _N. J. A. Sloane_
Bedeutung
Die On-Line Encyclopedia of Integer Sequences gilt vielen als wichtigste Referenz auf dem Gebiet der Folgen ganzer Zahlen. Die meisten Arbeiten, in denen solche Zahlenfolgen auftreten, enthalten Verweise auf die Datenbank.
Die Datenbank ist weltweit die größte ihrer Art und hat täglich mehrere tausend Anfragen. Ihr Erfolg ist teilweise dadurch begründet, dass die Daten kostenlos abgerufen werden können.
Aufgrund der OEIS entstanden einige mathematische Entdeckungen. So entdeckte jemand (R. D. North aus Colorado Springs), dass die bei Abschneiden der Leibniz-Reihe für Pi gebildete Zahl (Partialsumme der Leibniz-Reihe) kürzere und längere Abschnitte von Dezimalstellen aufwies, die mit denen von Pi übereinstimmten. Jonathan Borwein untersuchte die Dezimalstellen der Differenz und fand, dass sie bei Teilung durch 2 mit der Folge der Eulerschen Zahlen aus OEIS übereinstimmte. Mit Kollegen konnte er daraus eine exakte Formel für den Fehlerterm der Näherung von Pi durch die abgeschnittene Leibniz-Reihe geben.[4]
Geschichte
Neil Sloane begann 1964 damit, Folgen ganzer Zahlen zu sammeln, um seine Arbeit in der Kombinatorik zu erleichtern (was vermutlich auf ähnliche Folgen aus seiner Dissertation über neuronale Netzwerke zurückgeht). Er veröffentlichte zweimal Teile der Datenbank in Buchform:
- A Handbook of Integer Sequences (1973, ISBN 0-12-648550-X), mit 2372 Folgen.
- The Encyclopedia of Integer Sequences (1995, mit dem Mathematiker Simon Plouffe), ISBN 0-12-558630-2), mit 5488 Folgen.
Diese Bücher wurden begeistert aufgenommen, und nach der zweiten Veröffentlichung wurde die Sammlung zu groß (Verdoppelung des Umfangs ein Jahr nach der zweiten Publikation), um sie noch einmal als Buch zu veröffentlichen, und als die Datenbank 16.000 Einträge enthielt, entschied Sloane sich, die Daten online zugänglich zu machen, zuerst als E-Mail-Service (1995) und bald danach als Webservice (1996). Die Datenbank wächst seitdem um etwa 10.000 Einträge pro Jahr. Sloane selbst generierte die Einträge für über 170.000 Folgen (2015).[5] 2015 waren rund 4000 Nutzer bei OEIS registriert.
Nachdem Neil Sloane seine Datenbank fast 40 Jahre lang verwaltet hatte, übernahm 2002 eine Gruppe von Redakteuren einen Großteil der Wartungsarbeit. Seit 2009 hat sie die Form eines Wikis mit rund 100 freiwilligen Redakteuren. Oberste Instanz für Annahme oder Ablehnung eines Eintrags bleibt Neil Sloane nach wie vor, und seit Anfang 2006 wandelte sich die häufige Akzeptanz neuer Folgen in eine relativ restriktive Politik.
Als Ableger seiner Datenbank-Arbeit gründete Sloane 1998 das Journal of Integer Sequences. Im Oktober 2009 gingen das geistige Eigentum und der Betrieb der Server an die dazu gegründete OEIS Foundation.[6]
Sloane’s Gap
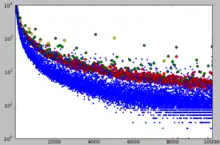
Stellt man in einem Diagramm dar, in wie vielen verschiedenen aller in der Datenbank gelisteten Folgen eine natürliche Zahl n jeweils auftaucht, folgt die Punktwolke für diese Häufigkeit Nn näherungsweise der Kurve Nn = 253.000.000 / n1,33. Ein Kuriosum in dieser Wolke/Kurve stellt ein Spalt (engl. gap) in dieser dar, der insbesondere für die Zahlen zwischen 300 und 10.000 zu beobachten ist. Dieser Spalt teilt scheinbar die mathematisch interessanten, in sehr vielen Folgen vorhandenen Zahlen von den uninteressanten. So befinden sich beispielsweise fast alle (99,7 %) der zwischen 300 und 10.000 auftauchenden Primzahlen im oberen Teil der Kurve. Auch ca. 95 % aller Quadratzahlen zwischen 300 und 10.000 sind dort zu finden. Während die Kurve selbst dem Erwartungswert entspricht, ist die Lücke allerdings auf rein mathematischem Weg bisher nicht zu erklären. Sie ist daher möglicherweise auch auf die Popularität bestimmter Zahlenfolgen in der mathematischen Forschung und somit auf soziale Faktoren zurückzuführen.[7]
Weblinks
- Die Online-Enzyklopädie der Zahlenfolgen (Suchformular der Datenbank, größtenteils englisch)
- Journal of Integer Sequences (englisch)
- Neil J. A. Sloane: The On-Line Encyclopedia of Integer Sequences. (PDF; 92 kB) In: Notices of the AMS, Vol. 50, Nr. 8, 2003, S. 912 (englisch)
- Neil J. A. Sloane: The On-Line Encyclopedia of Integer Sequences. In: Notices AMS, Oktober 2018
- Erica Klarreich, The Connoisseur of Number Sequences. In: Quanta Magazine, 6. August 2015
Einzelnachweise
- Style sheet for contributors
- OEIS: Explanation of Terms Used in Reply From
- Overview of the contribution process
- Jonathan Borwein, Peter Borwein, K. Dilcher: Pi, Euler Numbers and Asymptotic Expansions, American Mathematical Monthly, Band 96, 1989, S. 681–687
- Interview mit Quanta Magazine, 2015
- Transfer of IP in OEIS to The OEIS Foundation Inc. (Memento des Originals vom 6. Dezember 2013 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.
- Nicolas Gauvrit, Jean-Paul Delahaye, Hector Zenil: Sloane’s Gap: Do Mathematical and Social Factors Explain the Distribution of Numbers in the OEIS? arxiv:1101.4470