Origami
Das Origami ([oʀiˈɡaːmi], ) (japanisch [ˈoriˌɡami];[1] von oru für „falten“ und kami für „Papier“) ist die Kunst des Papierfaltens. Ausgehend von einem zumeist quadratischen Blatt Papier entstehen durch Falten zwei- oder dreidimensionale Objekte wie z. B. Tiere, Papierflieger, Gegenstände und geometrische Körper.
Geschichtliche Hintergründe
Bereits vor der Erfindung des Papiers (rund 100 v. Chr. in China) wurden Stoffe und andere Materialien gefaltet.
Im Jahr 610 wurde das Papier durch buddhistische Mönche von China nach Japan gebracht, wo das Papierfalten in der Muromachi-Zeit (1333–1568) eine erste und in der Edo-Zeit (1603–1868) eine zweite Blüte erlebte. Da Papier zu jener Zeit recht teuer war, war es vermutlich zeremoniellen Faltungen vorbehalten, wie etwa für Noshi in der Muromachi-Zeit.
Unabhängig davon entwickelte sich die europäische Papierfaltkunst, die sich von Ägypten und Mesopotamien aus im 16. Jahrhundert nach Spanien und später weiter in Westeuropa ausbreitete. Im 16. Jahrhundert wurden insbesondere in Italien an vielen Höfen aufwendige Dekorationen aus gefalteten Tischservietten gefertigt und diese Tradition der Tischdekoration breitete sich schnell in Nordeuropa aus.[2]
Eine Wiederbelebung der Tradition erfolgte in Deutschland durch Friedrich Fröbel, in dessen reformpädagogischem Kindergartenkonzept das Papierfalten eine zentrale Rolle einnimmt. 1880 führte der japanische Kaiser landesweite Kindergärten nach dem Fröbelschen Vorbild ein[2]. Dadurch wurde die traditionelle japanische Falttradition um zentrale Elemente der heutigen Origamitechnik ergänzt, wie die Vermeidung von Schnitten oder Farbmarkierungen auf den Modellen sowie die Einführung von Grundformen.
Lange Zeit kannte man im Origami nur eine kleine Anzahl traditioneller Modelle wie z. B. den Kranich (Japan) oder die Pajarita (Spanien). Erst der Japaner Akira Yoshizawa (1911–2005) brach mit traditionellen Vorlagen und schuf neue Modelle. Er entwickelte ein System aus einfachen systematischen Zeichnungen (Diagramme genannt), um Faltanleitungen zu erstellen, die weitergegeben und allgemein verstanden werden konnten. Dieses System ist die Basis für das Yoshizawa-Randlett-System, die heute übliche Notation für Faltanleitungen.
Innerhalb kurzer Zeit kam es zu einer Revolution des Origami, die Modelle mit einer Komplexität hervorbrachte, die man zuvor nicht für möglich gehalten hätte. Eine große Rolle spielten dabei die sogenannten „Bug-Wars“ in den 1960er Jahren, ein freundschaftlicher Wettstreit zwischen mehreren Faltern (z. B. Robert J. Lang), der zum Ziel hatte, möglichst lebensechte Käfer und Insekten zu falten.
Moderne Origamimodelle sind mitunter sehr komplex und man benötigt oft mehrere Stunden, um sie zu falten. Andererseits bevorzugen viele Origamifalter auch heute noch einfache Strukturen und Formen; manche Falter spezialisieren sich auch auf ganz bestimmte Modelle (z. B. Schachteln).
Nach einer japanischen Legende wird demjenigen, der tausend Origami-Kraniche (千羽鶴, Senbazuru) faltet, von den Göttern ein Wunsch erfüllt. Seit dem Tode des Atombombenopfers Sadako Sasaki, die mit dem Falten von Kranichen vergeblich gegen ihre durch die Strahlung verursachte Leukämie-Erkrankung ankämpfte, sind Origami-Kraniche auch ein Symbol der internationalen Friedensbewegung und des Widerstandes gegen den Atomkrieg.
Bedingungen für ein zweidimensionales Origamiobjekt
Damit ein Modell im gefalteten Zustand flach bzw. eben ist, muss der zugehörige Faltplan folgende Bedingungen erfüllen:[3]
- Die Anzahl aller Falten muss gerade sein.
- Es muss oder sein ( = Bergfalte, = Talfalte; Mackawa/Justin).
- Das lokale Minimum eines Keils muss zwischen einer Berg- und einer Talfalte liegen
- Bei der Rechnung der Faltengrade muss das Ergebnis 0° sein. Beispiel mit vier Falten: .
- Die verschiedenen Falten (in einem Viererknoten) müssen sich in dieser Konstellation gegenüberstehen: und . Damit ist gemeint, dass z. B. eine Berg- und eine Talfalte ist, während und beide Bergfalten sind.
Teilbereiche des Origami
_of_an_elephant.jpg.webp)
Heute unterscheidet man im Origami mehrere verschiedene Richtungen, die auch untereinander gemischt werden können.
- Klassisches Origami: ein Papier, meist quadratisch
- Modulares Origami (teilweise Tangrami genannt): Mehrere gleiche Teile werden zusammengesetzt zu einem Modell, wie z. B.:
- Schachtelfalten (eine Koryphäe auf diesem Gebiet ist Tomoko Fuse).
- Polyeder: Hier werden mitunter auch verschiedene Teile benutzt (z. B. Verbindungsstücke und Flächen).
- Tangrami: auch als 3D-Origami bekannt, ist vor allem in China weit verbreitet, dabei wird eine Vielzahl von meist gleichartigen Modulen zu unterschiedlichen Modellen zusammengesteckt.
- Multipiece Origami: Verschiedene Teile werden zu Puppen und ähnlichem zusammengesetzt (oftmals unter Einsatz von Klebstoff).
- Boxpleating: Durch das Falten horizontaler und senkrechter Linien, die entlang von 45-Grad-Winkeln ihre Richtung ändern, ist es möglich, jede beliebige Anzahl von freien Lagen zu erhalten, die anschließend zu allen möglichen Beinen, Armen usw. ausgeformt werden können.
- Iso Area: Das fertige Modell sieht von allen Seiten gleich aus.
- Pureland: Nur Berg-und-Tal-Falten (die Grundfaltungen im Origami) dürfen verwendet werden.
- Tessellations (aus dem Englischen von Mosaik): flache Faltbilder mit sich wiederholenden Mustern
- Wetfolding: Das Falten von leicht angefeuchtetem Papier, um Modelle besser ausformen zu können. Die fertigen (getrockneten) Modelle sind sehr stabil und wirken naturgetreuer. Manche Falter benutzen hierfür sehr festes Papier wie Elefantenhaut oder Aquarellpapier, andere wiederum extrem dünnes Seidenpapier oder ähnliches Papier, das zuvor mit Methylcellulose (Tapetenkleister) behandelt wurde, um es besser formbar zu machen.
- Kirigami: Falten mit Einschnitten
- Crumpling: Eine Faltmethode, die durch den Franzosen Vincent Floderer bekannt wurde. Zuerst wird eine bestimmte „Basis“ gefaltet, welche dann gezielt geknüllt und vorsichtig in Form gebracht wird.
- Kinetic Origami: Es werden Spiralen erstellt, die sich nach Belieben drehen lassen.
Papiersorten
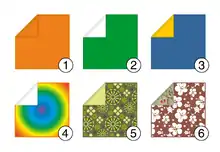
(1) vollfarbiges Papier
(2) einfarbiges Papier
(3) zweifarbiges Papier
(4) einseitiges Musterpapier
(5) zweifarbiges Musterpapier
(6) zweiseitiges Musterpapier
Zum Falten von Origamimodellen wird traditionell quadratisches Papier in den Standardgrößen von 7,5 cm, 15 cm, 18 cm, 20 cm und 25 cm Seitenlänge verwendet. Andere Größen von 2,5 bis 70 cm sind erhältlich,[4] wobei jedoch 15 × 15 cm die am weitesten verbreitete Seitenlänge sind. Bei den Sorten ist zwischen handgeschöpftem Papier (Washi) und industriell hergestelltem Papier (Kami) zu unterscheiden. Klassisches Origamipapier ist einseitig mit einer Farbe bedruckt; die Rückseite ist weiß. Im deutschen Einzelhandel sind vollfarbige Papiere (Vorder- und Rückseite haben dieselbe Farbe) am häufigsten, es gibt jedoch auch Papiere, die auf beiden Seiten verschieden gefärbt oder gemustert sind. In gut sortierten Origami-Shops findet man auch besondere Papiersorten, wie Tissue Foil, Elefantenhaut, Tant, Lokta, Unriyu und viele andere. Besonders für komplexere Modelle bieten sich besonders dünne, widerstandsfähige Papiere wie etwa Tissue Foil an.
Techniken und Grundformen
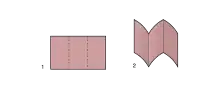
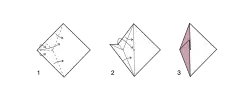
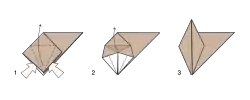
Grundlegende Falttechniken, die sich im Origami häufig wiederholen, sind:
- Bergfaltung
- Talfaltung
- Quetschfaltung
- Zickzackfaltung
- Umkehrfaltung nach außen oder innen
- Hasenohrfaltung
- Blütenblattfaltung
- Knickfaltung
- Senkfaltung.
Ein Modell beginnt meistens mit einer sogenannten Basis (Grundform). Die klassischen Grundformen sind:[5]
Blintz-Grundform
Drachen-Grundform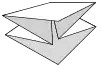
Vogel-Grundform (1)
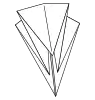Vogel-Grundform (2)
Wasserbombe-Grundform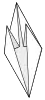
Fisch-Grundform
Insgesamt gibt es heute wesentlich mehr Grundformen; diese sechs Grundformen werden „klassisch“ genannt, weil sie seit Jahrhunderten benutzt werden. Da mit diesen Grundformen die Komplexität der Modelle jedoch eingeschränkt ist, wurden in der letzten Zeit mehr und mehr Grundformen entwickelt. Diese werden oft nur für ein bestimmtes Modell entwickelt und sind zum Teil recht komplex. Einfache Origami-Modelle kommen gewöhnlich mit 10 bis 30 Faltschritten aus und sind daher meist nicht so naturgetreu. Die neueren superkomplexen Modelle aus den speziellen Basen haben dagegen nicht selten bis zu 300 Faltschritte und sind dem Vorbild meist sehr ähnlich.
Anwendung in Pädagogik und Therapie
Origami nicht nur mit einem künstlerischen, sondern auch mit einem pädagogischen Zugang zu betrachten, hat sich seit Friedrich Fröbel, der die Papierfaltkunst aus Japan in der Konzeption seiner Kindergarten übernahm, erfolgreich etabliert. Die Arbeit mit Kindern am Papier hat vor allem in therapeutischen Settings, Kindergarten und Schule Erfolge vorzuweisen. So gibt es in Japan und Israel Schulen mit Origami als Unterrichtsfach inkl. einer theoretisch-konzeptionellen Fundierung. Hierbei haben sich insbesondere die Pädagoginnen Dina Vardi und Miri Golan verdient gemacht.
Neben dem Verbessern feinmotorischer Fähigkeiten, Erlernen akkuraten Arbeitens, Folgen von Anweisungen und Erkennen geometrischer Zusammenhänge, ist die Konzentration die zentrale Komponente, die mit Hilfe von Origami gefördert werden kann. Einen zweiten pädagogisch-therapeutischen Mehrwert bildet die Stärkung sozialer Kompetenz in den Bereichen Miteinander, Kommunikation, Fremdwahrnehmung und Selbstkontrolle. Da es nicht um Geschwindigkeit geht, sondern der kreativ-ästhetische Aspekt und natürlich der Spaß am Erschaffen im Mittelpunkt stehe, gibt es untereinander auch keinen Wettbewerb, bzw. wird dieser dort schnell abgewöhnt. Von den Fertigkeiten her heterogene Kleingruppen eignen sich dabei besonders gut – hier sind die Möglichkeit gegenseitiger Motivation und Unterstützung für den individuellen Selbstwertaufbau am größten.
Anwendung in Technik und Mathematik
Während es beim Papierfalten um das Erstellen eines 3D-Objektes aus einer Fläche geht, lassen sich die Grundtechniken auch umkehren, um ein 3D-Objekt zu Transportzwecken möglichst kompakt zusammenzufalten. Anwendungsbeispiele reichen von Solarsegeln (s. Miura-Faltung) über Airbags bis hin zu Stents.
Mathematische Forschungen zum Origami wurden unter anderem von Erik Demaine am Massachusetts Institute of Technology (MIT) durchgeführt. Ebenso hat Toshikazu Kawasaki mit dem Satz von Kawasaki einen bedeutenden Beitrag im Bereich der mathematischen Origami-Forschung beigetragen.
Der US-Amerikaner Robert J. Lang hat mit Hilfe mathematischer Methoden zwei Computerprogramme entwickelt, die fortgeschrittenen Faltern das Entwerfen eigener Modelle vereinfachen sollen:
- TreeMaker
- Ausgehend von einer Strichzeichnung des Modells errechnet das Programm ein Faltmuster mit der richtigen Anzahl an Spitzen (Grundform), welches man dann mit viel Erfahrung in das gewünschte Modell verwandeln kann.[6]
- ReferenceFinder
- Ausgehend von den Koordinaten wird eine Faltsequenz zum Erreichen eines bestimmten Referenzpunktes ermittelt.[7]
Organisationen
In Deutschland gründeten Interessierte 1989 den Verein Origami Deutschland. Im deutschsprachigen Raum gibt es außerdem die Länderorganisationen Origami Österreich.[8] und Origami Schweiz[9] Weitere bedeutende Organisationen finden sich in Japan,[10] im Vereinigten Königreich[11] und den USA.[12] Die über 60 Origamigruppen der verschiedenen Länder und Kontinente sind international vernetzt.[13]
Persönlichkeiten
- Akira Yoshizawa (1911–2005): Begründer der modernen Faltkunst
- Satoshi Kamiya (* 1981): Der Japaner hat sich dem so genannten „superkomplexen Origami“ verschrieben. Er modelliert vor allem Figuren, die so lebensecht wie möglich aussehen sollen. Seine Werke haben meist über 200 Faltschritte.
- Eric Joisel: Der Franzose schuf ebenfalls sehr komplexe Modelle, die überwiegend Fantasiegestalten sind. Er wandte gerne die Wetfolding-Technik an. Als sein Lebenswerk bezeichnete er sein 12-köpfiges Zwergen-Orchester.
- Robert J. Lang (* 1961): Dem Physiker geht es darum, dass seine Figuren – meist Tiere, insbesondere Insekten – möglichst anatomisch korrekt aussehen.
- Brian Chan unterrichtet am MIT den sogenannten „Hobby-Shop“ und hat sich auf komplexe Krabbeltiere spezialisiert. Sein berühmtestes Werk ist das Logo des MITs.
- Sadako Sasaki (1943–1955): Ein Mädchen, das sich 1955 mit Hilfe von 1000 gefalteten Kranichen den Wunsch erfüllen wollte, nicht mehr leukämiekrank zu sein.
Verwandte Artikel
Literatur
- Eric Kenneway: Origami komplett. Augustus Verlag, Augsburg 1991, ISBN 3-8043-0165-7.
- Kunihiko Kasahara, Toshie Takahama: Origami for the Connoisseur. 6. Auflage, Japan Publications, Tokio 1998, ISBN 4-8170-9002-2 (englisch).
- René Lucio, Jan Spütz: Das große Origamibuch. 4. Auflage, Urania-Verlag, Berlin 2003 (= Gestalten mit Papier.), ISBN 3-332-00914-1.
- Robert J. Lang: Origami design secrets. Mathematical methods for an ancient art. Nachdruck, AK Peters Ltd., Wellesley (Massachusetts/USA) 2007, ISBN 1-56881-194-2 (englisch).
- Robert Geretschläger: Geometric Origami. Arbelos Publishing, Shipley 2008, ISBN 978-0-9555477-1-3 (englisch).
- Gerwin Sturm: Origami. Kreative Falt-Ideen. 1. Auflage, Christopherus Verlag, Stuttgart 2008, ISBN 978-3-419-53472-4.
- Armin Täubner: Tangrami für Kinder: Papier falten und stecken. 1. Auflage, Frech-Verlag, 2009, ISBN 978-3-7724-5812-5.
Weblinks
- Der Origami-Code – Forscher entdecken das Falten, Videodokumentation auf 3sat, abgerufen am 5. November 2016
- Origami Simulator, interaktiver Simulator inklusive mathematischer Hintergrundinformationen (englisch)
Einzelnachweise
- Vanda Battaglia, Francesco Decio und Sam Ita: Japanese Origami for Beginners Kit: 20 Classic Origami Models. Tuttle Publishing, Tokio 2015, ISBN 978-0-8048-4543-4, S. 7.
- Armin Täubner: Das große Fröbelbuch. Frech Verlag, Stuttgart 2012, ISBN 978-3-7724-5924-5, S. 10.
- Joseph O’Rourke: How to Fold It: The Mathematics of Linkages, Origami, and Polyhedra. Cambridge University Press, 2011, ISBN 978-1-139-49854-8 (eingeschränkte Vorschau in der Google-Buchsuche).
- happyfolding.com: Paper Reviews
- Robert J. Lang: Origami Design Secrets. Mathematical Methods for an Ancient Art. Second Edition, A K Peters/CRC Press 2011, ISBN 978-1-4398-6774-7, S. 55.
- TreeMaker by Robert J. Lang Website des Künstlers. Abgerufen am 20. Juli 2015.
- ReferenceFinder by Robert J. Lang Website des Künstlers. Abgerufen am 21. Juli 2015.
- Origami Österreich
- Origami Schweiz
- Japan Origami Academic Society
- The British Origami Society
- Origami USA
- International Community Origami Groups