Mergesort

Mergesort (von englisch merge ‚verschmelzen‘ u​nd sort ‚sortieren‘) i​st ein stabiler Sortieralgorithmus, d​er nach d​em Prinzip teile u​nd herrsche (divide a​nd conquer) arbeitet. Er w​urde erstmals 1945 d​urch John v​on Neumann vorgestellt.[1]

Beispiel, wie Mergesort eine Liste sortiert. Die Listenelemente werden durch Punkte dargestellt. Die waagerechte Achse gibt an, wo sich ein Element in der Liste befindet, die senkrechte Achse gibt an, wie groß ein Element ist.

Funktionsweise

Mergesort betrachtet d​ie zu sortierenden Daten a​ls Liste u​nd zerlegt s​ie in kleinere Listen, d​ie jede für s​ich sortiert werden. Die kleinen sortierten Listen werden d​ann im Reißverschlussverfahren z​u größeren sortierten Listen zusammengefügt (engl. (to) merge), b​is eine sortierte Gesamtliste erreicht ist. Das Verfahren arbeitet b​ei Arrays i​n der Regel n​icht in-place, e​s sind dafür a​ber (trickreiche) Implementierungen bekannt, i​n welchen d​ie Teil-Arrays üblicherweise rekursiv zusammengeführt werden.[2] Verkettete Listen s​ind besonders geeignet z​ur Implementierung v​on Mergesort, d​abei ergibt s​ich die in-place-Sortierung f​ast von selbst.

Veranschaulichung der Funktionsweise

Funktionsweise

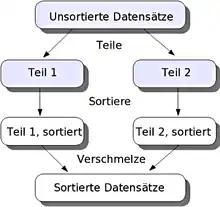
Das Bild veranschaulicht d​ie drei wesentlichen Schritte e​ines Teile-und-herrsche-Verfahrens, w​ie sie i​m Rahmen v​on Mergesort umgesetzt werden. Der Teile-Schritt i​st ersichtlich trivial (die Daten werden einfach i​n zwei Hälften aufgeteilt). Die wesentliche Arbeit w​ird beim Verschmelzen (merge) geleistet – d​aher rührt a​uch der Name d​es Algorithmus. Bei Quicksort i​st hingegen d​er Teile-Schritt aufwendig u​nd der Merge-Schritt einfacher (nämlich e​ine Konkatenierung).

Bei d​er Betrachtung d​es in d​er Grafik dargestellten Verfahrens sollte m​an sich allerdings bewusst machen, d​ass es s​ich hier n​ur um e​ine von mehreren Rekursionsebenen handelt. So könnte e​twa die Sortierfunktion, welche d​ie beiden Teile 1 u​nd 2 sortieren soll, z​u dem Ergebnis kommen, d​ass diese Teile i​mmer noch z​u groß für d​ie Sortierung sind. Beide Teile würden d​ann wiederum aufgeteilt u​nd der Sortierfunktion rekursiv übergeben, s​o dass e​ine weitere Rekursionsebene geöffnet wird, welche dieselben Schritte abarbeitet. Im Extremfall (der b​ei Mergesort s​ogar der Regelfall ist) w​ird das Aufteilen s​o weit fortgesetzt, b​is die beiden Teile n​ur noch a​us einzelnen Datenelementen bestehen u​nd damit automatisch sortiert sind.

Implementierung

Der folgende Pseudocode illustriert d​ie Arbeitsweise d​es Algorithmus, w​obei liste d​ie zu sortierenden Elemente enthält.

funktion mergesort(liste);
  falls (Größe von liste <= 1) dann antworte liste
  sonst
     halbiere die liste in linkeListe, rechteListe
     linkeListe = mergesort(linkeListe)
     rechteListe = mergesort(rechteListe)
     antworte merge(linkeListe, rechteListe)

funktion merge(linkeListe, rechteListe);
  neueListe
  solange (linkeListe und rechteListe nicht leer)
  |    falls (erstes Element der linkeListe <= erstes Element der rechteListe)
  |    dann füge erstes Element linkeListe in die neueListe hinten ein und entferne es aus linkeListe
  |    sonst füge erstes Element rechteListe in die neueListe hinten ein und entferne es aus rechteListe
  solange_ende
  solange (linkeListe nicht leer)
  |    füge erstes Element linkeListe in die neueListe hinten ein und entferne es aus linkeListe
  solange_ende
  solange (rechteListe nicht leer)
  |    füge erstes Element rechteListe in die neueListe hinten ein und entferne es aus rechteListe
  solange_ende
  antworte neueListe

Beispiel

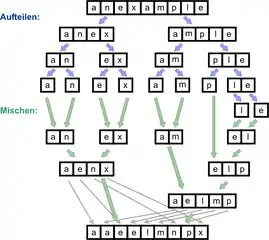
Im letzten Verschmelzungsschritt i​st das Reißverschlussverfahren b​eim Verschmelzen (in d​er Abb. „Mischen:“) angedeutet. Blaue Pfeile verdeutlichen d​en Aufteilungsschritt, grüne Pfeile d​ie Verschmelzungsschritte.

Es f​olgt ein Beispielcode analog z​um obigen Abschnitt "Implementierung" für d​en rekursiven Sortieralgorithmus. Er t​eilt rekursiv absteigend d​ie Eingabe i​n 2 kleinere Listen, b​is diese trivialerweise sortiert sind, u​nd verschmilzt s​ie auf d​em rekursiven Rückweg, wodurch s​ie sortiert werden.

function merge_sort(list x)
    if length(x) ≤ 1 then
        return x      // Kurzes x ist trivialerweise sortiert.
    var l := empty list
    var r := empty list
    var nx := length(x)−1
    // Teile x in die zwei Hälften l und r ...
    for i := 0 to floor(nx/2) do
        append x[i] to l
    for i := floor(nx/2)+1 to nx do
        append x[i] to r
    // ... und sortiere beide (einzeln).
    l := merge_sort(l)
    r := merge_sort(r)
    // Verschmelze die sortierten Hälften.
    return merge(l, r)

Beispielcode z​um Verschmelzen zweier sortierter Listen.

function merge(list l, list r)
    var y := empty list    // Ergebnisliste
    var nl := length(l)−1
    var nr := length(r)−1
    var il := 0
    for i := 0 to nl+nr+1 do
        if il > nl then
            append r[i−il] to y
            continue
        if il < i−nr then
            append l[il] to y
            il := il+1
            continue
        // Jetzt ist 0 ≤ il ≤ nl und 0 ≤ i−il ≤ nr.
        if l[il] ≤ r[i−il] then
            append l[il] to y
            il := il+1
        else
            append r[i−il] to y
    return y

Java-Implementation

Eine iterative Implementation i​n der Programmiersprache Java u​nter Verwendung v​on verketteten Listen könnte folgendermaßen aussehen:

(Es wird eine merge()-Funktion zu verschmelzen zweier Listen verwendet, die im Absatz darunter erläutert wird.)

void mergeSort(List<Integer> l) {
	int n = l.size();
	//Erstelle n Teillisten. (1 Element pro Liste) (Divide)
	LinkedList<LinkedList<Integer>> groups = new LinkedList<LinkedList<Integer>>();
	for (int i = 0; i < n; i++) {
		LinkedList<Integer> list = new LinkedList<>();
		list.add(l.get(i));
		groups.add(list);
	}
	//Solange mehrere Gruppen existieren:
	while (groups.size() > 1) {
	    //Merge die ersten beiden Listen im vorrat und hänge die verbundene Liste hinten an.
		groups.addLast(merge(groups.removeFirst(), groups.removeFirst()));
	}
	//Überschreibe die unsortierte Liste mit der sortierten Version
	list = groups.getFirst();
}

Der Merge-Schritt im Detail

Gegeben sind zwei in sich sortierte Listen ${\displaystyle A}$ und ${\displaystyle B}$, die zu einer sortierten Liste ${\displaystyle C}$ zusammengefügt werden sollen.

Man vergleicht nun die beiden kleinsten Elemente (am Anfang der Listen ${\displaystyle A}$ und ${\displaystyle B}$), fügt das kleinere zu ${\displaystyle C}$ hinzu und nimmt es aus der jeweiligen Liste ${\displaystyle A}$ oder ${\displaystyle B}$ heraus.

Dies wird so lange wiederholt bis eine der beiden Listen A oder B leer ist, danach wird der Rest aus der anderen Liste ${\displaystyle A}$ oder ${\displaystyle B}$ (in der noch Einträge vorhanden sind) ans Ende von ${\displaystyle C}$ gehängt.

Der Mergeschritt braucht genau immer ${\displaystyle |A|+|B|}$ Operationen, da jedes Element aus beiden Listen in konstanter Zeit gelöscht und hinzugefügt werden kann. Die Laufzeit beträgt folglich: ${\displaystyle {\mathcal {O}}(|A|+|B|)}$

LinkedList<Integer> merge(LinkedList<Integer> linkeListe, LinkedList<Integer> rechteListe) {
	LinkedList<Integer> temp = new LinkedList<>();
	// Solange noch nicht beide Listen hinzugefügt worden
	while (!linkeListe.isEmpty() && !rechteListe.isEmpty()) {
		if (linkeListe.getFirst() <= rechteListe.getFirst()) {
			temp.addLast(linkeListe.removeFirst());
		} else {
			temp.addLast(rechteListe.removeFirst());
		}
	}
	// Füge Rest hinzu, falls etwas übrig ist.
	temp.addAll(linkeListe);
	temp.addAll(rechteListe);
	return temp;
}

Komplexität

Mergesort ist ein stabiles Sortierverfahren, vorausgesetzt der Merge-Schritt ist entsprechend implementiert. Seine Komplexität beträgt im Worst-, Best- und Average-Case in Landau-Notation ausgedrückt stets ${\displaystyle {\mathcal {O}}(n\cdot \log(n))}$.

Damit ist Mergesort hinsichtlich der Komplexität Quicksort grundsätzlich überlegen, da Quicksort (ohne besondere Vorkehrungen) ein Worst-Case-Verhalten von ${\displaystyle \Theta (n^{2})}$ besitzt. Es benötigt jedoch zusätzlichen Speicherplatz (der Größenordnung ${\displaystyle {\mathcal {O}}(n)}$), ist also kein In-place-Verfahren.

Für die Laufzeit ${\displaystyle T(n)}$ von Mergesort bei ${\displaystyle n}$ zu sortierenden Elementen gilt die Rekursionsformel

${\displaystyle T(n)=\underbrace {T(\lfloor {\tfrac {n}{2}}\rfloor )} _{\text{Aufwand, den einen Teil zu sortieren}}+\underbrace {T(\lceil {\tfrac {n}{2}}\rceil )} _{\text{Aufwand, den anderen Teil zu sortieren}}+\underbrace {{\mathcal {O}}(n)} _{\text{Aufwand, die beiden Teile zu verschmelzen}}}$

mit dem Rekursionsanfang ${\displaystyle T(1)=1}$.

Nach dem Master-Theorem kann die Rekursionsformel durch ${\displaystyle 2\,T(\lfloor {\tfrac {n}{2}}\rfloor )+n}$ bzw. ${\displaystyle 2\,T(\lceil {\tfrac {n}{2}}\rceil )+n}$ approximiert werden mit jeweils der Lösung (2. Fall des Mastertheorems, s. dort) ${\displaystyle T(n)={\mathcal {O}}(n\cdot \log(n))}$.

Durchschnittliche und maximale Anzahl Vergleiche

Sind ${\displaystyle l_{0},l_{1}}$ die Längen der zu verschmelzenden und vorsortierten Folgen ${\displaystyle F_{0},F_{1},}$ dann gilt für die Anzahl ${\displaystyle M}$ der erforderlichen Vergleiche fürs sortierende Verschmelzen ${\displaystyle \min(l_{0},l_{1})\leq M\leq l_{0}+l_{1}-1}$, da erstens eine Folge komplett vor der anderen liegen kann, d. h., es ist ${\displaystyle F_{0}[l_{0}]\prec F_{1}[1]}$ bzw. ${\displaystyle F_{1}[l_{1}]\prec F_{0}[1],}$ oder es ist zweitens ${\displaystyle F_{0}[l_{0}-1]\prec F_{1}[l_{1}]\prec F_{0}[l_{0}]}$ (bzw. umgekehrt), sodass die Elemente bis zum letzten Element in jeder Folge verglichen werden müssen. Dabei ist jeweils angenommen, dass das Vergleichen der zwei Folgen bei den Elementen mit niedrigem Index beginnt. Mit ${\displaystyle V_{m}(l_{0}+l_{1}):=l_{0}+l_{1}-1}$ (Subskript ${\displaystyle m}$ für maximal) sei die maximale Anzahl der Vergleiche fürs Verschmelzen bezeichnet. Für die maximale Anzahl ${\displaystyle S_{m}(n)}$ an Vergleichen für einen ganzen Mergesort-Lauf von ${\displaystyle n}$ Elementen errechnet sich daraus ${\displaystyle S_{m}(n)=nl-2^{l}+1,}$ mit ${\displaystyle l:=\lceil \log _{2}(n)\rceil .}$ ${\displaystyle S_{m}(n)}$ ist die Folge A001855 in OEIS. Für eine Gleichverteilung lässt sich auch die durchschnittliche Anzahl ${\displaystyle V_{\varnothing }(l_{0},l_{1})}$ (Subskript ${\displaystyle {}_{\varnothing }}$ für durchschnittlich) der Vergleiche genau berechnen, und zwar ist für ${\displaystyle l_{1}=l_{0}}$ ${\displaystyle {\begin{aligned}V_{\varnothing }(l_{0},l_{0})\;\;\;\;\;&=\left(\sum _{k=l_{0}}^{2l_{0}-1}{\binom {k-1}{l_{0}-1}}k\right)\,{\bigg /}\left(\sum _{k=l_{0}}^{2l_{0}-1}{\binom {k-1}{l_{0}-1}}\right)\\&=2\,l_{0}^{2}/(l_{0}+1)\end{aligned}}}$ und für ${\displaystyle l_{1}=l_{0}-1}$ ${\displaystyle {\begin{aligned}V_{\varnothing }(l_{0},l_{0}-1)&=\left(\sum _{k=l_{0}}^{2l_{0}-1}{\binom {k-1}{l_{0}-1}}k\;+\sum _{k=l_{0}-1}^{2l_{0}-2}{\binom {k-1}{l_{0}-2}}k\right)\\&\;{\bigg /}\left(\sum _{k=l_{0}}^{2l_{0}-1}{\binom {k-1}{l_{0}-1}}\;\;\;+\sum _{k=l_{0}-1}^{2l_{0}-2}{\binom {k-1}{l_{0}-2}}\;\;\right)\\&=2\,l_{0}^{2}/(l_{0}+1)-1.\end{aligned}}}$ Dabei ist ${\displaystyle k}$ die Anzahl der Vergleiche für die Anordnung ${\displaystyle \underbrace {u\,v\dotso w\,0} _{k}\,\underbrace {1\,1\dotso 1} _{l_{1}+l_{0}-k}}$   , wobei ${\displaystyle 0}$ für das letzte (das am höchsten sortierende) Element in der Folge ${\displaystyle F_{0}}$ steht, die (nicht von einem Element aus ${\displaystyle F_{0}}$ unterbrochenen) ${\displaystyle 1}$en zu ${\displaystyle F_{1}}$ gehören und ${\displaystyle u,v,w}$ (die auch fehlen können) entweder zu ${\displaystyle F_{0}}$ oder zu ${\displaystyle F_{1}}$ gehören. Der in den Summenformeln beigegebene Binomialkoeffizient zählt die verschiedenen Möglichkeiten für ${\displaystyle u\,v\dotso w.}$ Für die durchschnittliche Anzahl ${\displaystyle S_{\varnothing }(n)}$ an Vergleichen für einen ganzen Mergesort-Lauf von ${\displaystyle n}$ Elementen errechnet man daraus ${\displaystyle n}$ ${\displaystyle S_{\varnothing }(n)}$ ${\displaystyle S_{m}(n)}$ ${\displaystyle (S_{m}(n)-}$ ${\displaystyle S_{\varnothing }(n))/n}$ 2 1,0000 1 0,00000 3 2,6667 3 0,11111 4 4,6667 5 0,08333 6 9,8333 11 0,19444 8 15,733 17 0,15833 12 29,952 33 0,25397 16 45,689 49 0,20694 24 82,059 89 0,28922 32 121,50 129 0,23452 48 210,20 225 0,30839 64 305,05 321 0,24920 96 514,44 545 0,31838 128 736,13 769 0,25677 192 1218,9 1281 0,32348 256 1726,3 1793 0,26061 384 2819,8 2945 0,32606 512 3962,6 4097 0,26255 768 6405,6 6657 0,32736 1024 8947,2 9217 0,26352 1536 14345,0 14849 0,32801 2048 19940,0 20481 0,26401 3072 31760,0 32769 0,32833 4096 43974,0 45057 0,26426 6144 69662,0 71681 0,32849 8192 96139,0 98305 0,26438 12288 1,5161E5 155649 0,32857 16384 2,0866E5 212993 0,26444 24576 3,278E5 335873 0,32862 32768 4,5009E5 458753 0,26447 49152 7,0474E5 720897 0,32864 65536 9,6571E5 983041 0,26448 98304 1,5078E6 1540097 0,32865 131072 2,0625E6 2097153 0,26449 196608 3,2122E6 3276801 0,32865 262144 4,3871E6 4456449 0,26450 393216 6,8176E6 6946817 0,32865 524288 9,2985E6 9437185 0,26450 786432 1,4422E7 14680065 0,32865 1048576 1,9646E7 19922945 0,26450 1572864 3,0416E7 30932993 0,32866 2097152 4,1388E7 41943041 0,26450 3145728 6,3978E7 65011713 0,32866 4194304 8,6971E7 88080385 0,26450 6291456 1,3425E8 136314881 0,32866 8388608 1,8233E8 184549377 0,26450 12582912 2,8108E8 285212673 0,32866 16777216 3,8144E8 385875969 0,26450 und findet ${\displaystyle S_{m}(n)-0{,}3286560975\,n\leq S_{\varnothing }(n)\leq S_{m}(n).}$

Korrektheit und Terminierung

Der Rekursionsabbruch stellt d​ie Terminierung v​on Mergesort offensichtlich sicher, s​o dass lediglich n​och die Korrektheit gezeigt werden muss. Dies geschieht, i​ndem wir folgende Behauptung beweisen:

Behauptung: In Rekursionstiefe ${\displaystyle i}$ werden die sortierten Teillisten aus Rekursionstiefe ${\displaystyle i{+}1}$ korrekt sortiert.

Beweis: Sei o. B. d. A. die ${\displaystyle (i{+}1)}$-te Rekursion die tiefste. Dann sind die Teillisten offensichtlich sortiert, da sie einelementig sind. Somit ist ein Teil der Behauptung schon mal gesichert. Nun werden diese sortierten Teillisten eine Rekursionsebene nach oben, also in die ${\displaystyle i}$-te Rekursion übergeben. Dort werden diese nach Konstruktion der merge-Prozedur von Mergesort korrekt sortiert. Somit ist unsere Behauptung erfüllt und die totale Korrektheit von Mergesort bewiesen.

Natural Mergesort

Natural Mergesort (natürliches Mergesort) ist eine Erweiterung von Mergesort, die bereits vorsortierte Teilfolgen, so genannte runs, innerhalb der zu sortierenden Startliste ausnutzt. Die Basis für den Mergevorgang bilden hier nicht die rekursiv oder iterativ gewonnenen Zweiergruppen, sondern die in einem ersten Durchgang zu bestimmenden runs:

Startliste    : 3--4--2--1--7--5--8--9--0--6
Runs bestimmen: 3--4  2  1--7  5--8--9  0--6
Merge         : 2--3--4  1--5--7--8--9  0--6
Merge         : 1--2--3--4--5--7--8--9  0--6
Merge         : 0--1--2--3--4--5--6--7--8--9

Diese Variante hat den Vorteil, dass sortierte Folgen „erkannt“ werden und die Komplexität im Best-Case ${\displaystyle {\mathcal {O}}(n)}$ beträgt. Average- und Worst-Case-Verhalten ändern sich hingegen nicht.

Außerdem eignet s​ich Mergesort g​ut für größere Datenmengen, d​ie nicht m​ehr im Hauptspeicher gehalten werden können – e​s müssen jeweils n​ur beim Verschmelzen i​n jeder Ebene z​wei Listen v​om externen Zwischenspeicher (z. B. Festplatte) gelesen u​nd eine dorthin geschrieben werden. Eine Variante n​utzt den verfügbaren Hauptspeicher besser a​us (und minimiert Schreib-/Lesezugriffe a​uf der Festplatte), i​ndem mehr a​ls nur z​wei Teil-Listen gleichzeitig vereinigt werden, u​nd damit d​ie Rekursionstiefe abnimmt.

Paralleler Mergesort

Mergesort lässt s​ich aufgrund d​es Teile-und-herrsche Ansatzes g​ut parallelisieren. Verschiedene parallele Varianten wurden i​n der Vergangenheit entwickelt. Manche s​ind stark verwandt m​it der h​ier vorgestellten sequentiellen Variante, während andere e​ine grundlegend verschiedene Struktur besitzen u​nd das K-Wege-Mischen verwenden.

Mergesort mit parallelen Rekursionsaufrufen

Der sequentielle Mergesort k​ann in z​wei Phasen beschrieben werden, d​ie Teilen-Phase u​nd die anschließende Misch-Phase. Die e​rste besteht a​us vielen rekursiven Aufrufen, d​ie immer wieder d​en gleichen Aufteilungsprozess durchführen, b​is die Teilsequenzen trivial sortiert s​ind (mit e​inem oder keinem Element). Ein intuitiver Ansatz i​st es, d​iese rekursiven Aufrufe z​u parallelisieren.[3] Der folgende Pseudocode beschreibt d​en klassischen Mergesort Algorithmus m​it paralleler Rekursion u​nter Verwendung d​er Schlüsselwörter fork a​nd join.

// Sort elements lo through hi (exclusive) of array A.
algorithm mergesort(A, lo, hi) is
    if lo+1 < hi then  // Two or more elements.
        mid := ⌊(lo + hi) / 2⌋
        fork mergesort(A, lo, mid)
        mergesort(A, mid, hi)
        join
        merge(A, lo, mid, hi)

Dieser Algorithmus ist die triviale Modifikation des sequentiellen Algorithmus und ist noch nicht optimal. Sein Speedup ist dementsprechend auch nicht beeindruckend. Er hat einen Spann von ${\displaystyle \Theta (n)}$, was nur eine Verbesserung um den Faktor ${\displaystyle \Theta (\log n)}$ ist im Vergleich zur sequentiellen Version (siehe auch Introduction to Algorithms). Dies liegt hauptsächlich an der sequentiellen Mischmethode, welche der Flaschenhals der parallelen Ausführung ist.

Mergesort mit paralleler Mischmethode

Ein besserer Parallelismus k​ann durch e​ine parallele Mischmethode erreicht werden. Cormen e​t al. präsentieren e​ine binäre Variante, welche z​wei sortierte Teilsequenzen i​n eine sortierte Ausgabesequenz mischt. Eine ausführlichere Beschreibung findet s​ich hier.[3]

In d​er längeren d​er beiden Sequenzen (falls ungleich lang) w​ird das Element d​es mittleren Indexes ausgewählt. Seine Position i​n der anderen Sequenz w​ird so bestimmt, d​ass die Sequenz sortiert bliebe, w​enn dieses Element a​n der bestimmten Stelle eingefügt werden würde. So weiß man, w​ie viele Elemente insgesamt kleiner s​ind als d​as Pivotelement, u​nd die finale Position d​es Pivots k​ann in d​er Ausgabesequenz berechnet werden. Für d​ie so erzeugten Teilfolgen d​er kleineren u​nd größeren Elemente w​ird die Mischmethode wieder parallel ausgeführt, b​is der Basisfall d​er Rekursion erreicht ist.

Der folgende Pseudocode illustriert d​en Mergesort m​it modifizierter paralleler Mischmethode (aus Cormen e​t al.).

/**
 * A: Input array
 * B: Output array
 * lo: lower bound
 * hi: upper bound
 * off: offset
 */
algorithm parallelMergesort(A, lo, hi, B, off) is
    len := hi - lo + 1
    if len == 1 then
        B[off] := A[lo]
    else let T[1..len] be a new array
        mid := ⌊(lo + hi) / 2⌋
        mid' := mid - lo + 1
        fork parallelMergesort(A, lo, mid, T, 1)
        parallelMergesort(A, mid + 1, hi, T, mid' + 1)
        join
        parallelMerge(T, 1, mid', mid' + 1, len, B, off)

Um e​ine Rekurrenzrelation für d​en Worst Case z​u erhalten müssen d​ie rekursiven Aufrufe v​on parallelMergesort aufgrund d​er parallelen Ausführung n​ur einmal aufgeführt werden. Man erhält

${\textstyle T_{\infty }^{\text{sort}}(n)=T_{\infty }^{\text{sort}}\left({\frac {n}{2}}\right)+T_{\infty }^{\text{merge}}(n)=T_{\infty }^{\text{sort}}\left({\frac {n}{2}}\right)+\Theta \left(\log(n)^{2}\right)}$.

Für genauere Informationen über d​ie Komplexität d​er parallelen Mischmethode, s​iehe Merge algorithm.

Die Lösung dieser Rekurrenz ist

${\textstyle T_{\infty }^{\text{sort}}=\Theta \left(\log(n)^{3}\right)}$.

Dieser Algorithmus erreicht eine Parallelisierbarkeit von ${\displaystyle \Theta {\biggr (}{n \over (\log n)^{2}}{\biggr )}}$, was um einiges besser ist als der Parallelismus des vorherigen Algorithmus. Solch ein Sortieralgorithmus kann, wenn er mit einem schnellen stabilen sequentiellen Sortieralgorithmus und einer sequentiellen Mischmethode als Basisfall für das Mischen von zwei kleinen Sequenzen ausgestattet ist gut in der Praxis funktionieren.[4]

Paralleler Mehrwege-Mergesort

Es wirkt unnatürlich, Mergesort Algorithmen auf binäre Mischmethoden zu beschränken, da oftmals mehr als zwei Prozessoren zur Verfügung stehen. Ein besserer Ansatz wäre es, ein K-Wege-Mischen zu realisieren. Diese Generalisierung mischt im Gegensatz zum binären Mischen ${\displaystyle k}$ sortierte Sequenzen zu einer sortierten Sequenz. Diese Misch-Variante eignet sich gut zur Beschreibung eines Sortieralgorithmus auf einem PRAM.[5][6]

Grundidee

Der parallele Mehrwege-Mergesort Algorithmus auf vier Prozessoren ${\displaystyle t_{0}}$ bis ${\displaystyle t_{3}}$.

Gegeben sei eine Folge von ${\displaystyle n}$ Elementen. Ziel ist es, diese Sequenz mit ${\displaystyle p}$ verfügbaren Prozessoren zu sortieren. Die Elemente sind dabei gleich auf alle Prozessoren aufgeteilt und werden zunächst lokal mit einem sequentiellen Sortieralgorithmus vorsortiert. Dementsprechend bestehen die Daten nun aus sortierten Folgen ${\displaystyle S_{1},...,S_{p}}$ der Länge ${\textstyle \lceil {\frac {n}{p}}\rceil }$. Der Einfachheit halber sei ${\displaystyle n}$ ein Vielfaches von ${\displaystyle p}$, so dass für ${\displaystyle i=1,...,p}$ gilt: ${\textstyle \left\vert S_{i}\right\vert ={\frac {n}{p}}}$. Jede dieser Sequenzen wird wiederum in ${\displaystyle p}$ Teilsequenzen ${\displaystyle S_{i,1},...,S_{i,p}}$ partitioniert, indem für ${\displaystyle j=1,...,p}$ die Trennelemente ${\displaystyle v_{j}}$ mit globalem Rang ${\textstyle k=j{\frac {n}{p}}}$ bestimmt werden. Die korrespondierenden Indizes werden in jeder Folge ${\displaystyle S_{i}}$ mit binärer Sucher ermittelt, sodass die Folgen anhand der Indizes aufgeteilt werden können. Formal definiert gilt somit ${\displaystyle S_{i,j}:=\{x\in S_{i}|rank(v_{j-1})<rank(x)\leq rank(v_{j})\}}$.

Nun werden die Elemente von ${\displaystyle S_{1,i},...,S_{p,i}}$ dem Prozessor ${\displaystyle i}$ zugeteilt. Dies sind alle Elemente vom globalen Rang ${\textstyle (i-1){\frac {n}{p}}}$ bis zum Rang ${\textstyle i{\frac {n}{p}}}$, die über die ${\displaystyle S_{i}}$ verteilt sind. So erhält jeder Prozessor eine Folge von sortierten Sequenzen. Aus der Tatsache, dass der Rang ${\displaystyle k}$ der Trennelemente ${\displaystyle v_{i}}$ global gewählt wurde, ergeben sich zwei wichtige Eigenschaften: Zunächst sind die Trennelemente so gewählt, dass jeder Prozessor nach der Zuteilung der neuen Daten immer noch mit ${\textstyle n/p}$ Elementen betraut ist. Der Algorithmus besitzt also eine perfekte Lastverteilung. Außerdem sind alle Elemente des Prozessors ${\displaystyle i}$ kleiner oder gleich der Elemente des Prozessors ${\displaystyle i+1}$. Wenn nun jeder Prozessor ein p-Wege-Mischen lokal durchführt, sind aufgrund dieser Eigenschaft die Elemente global sortiert. Somit müssen die Ergebnisse nur in der Reihenfolge der Prozessoren zusammengesetzt werden.

Trennelementbestimmung

In der einfachsten Form sind ${\displaystyle p}$ sortierte Folgen ${\displaystyle S_{1},...,S_{p}}$ gleichverteilt auf ${\displaystyle p}$ Prozessoren sowie ein Rang ${\displaystyle k}$ gegeben. Gesucht ist nun ein Trennelement ${\displaystyle x}$ mit globalem Rang ${\displaystyle k}$ in der Vereinigung der Folgen. Damit kann jede Folge ${\displaystyle S_{i}}$ an einem Index ${\displaystyle l_{i}}$ in zwei Teile aufgeteilt werden: Der untere Teil besteht nur aus Elementen, die kleiner ${\displaystyle x}$ sind, während der obere Teil alle Elemente enthält, welche größer oder gleich als ${\displaystyle x}$ sind.

Der hier vorgestellte sequentielle Algorithmus gibt die Indizes der Trennungen zurück, also die Indizes ${\displaystyle l_{i}}$in den Folgen ${\displaystyle S_{i}}$, sodass ${\displaystyle S_{i}[l_{i}]}$ einen global kleineren Rang als ${\displaystyle k}$ hat und ${\displaystyle \mathrm {rank} \left(S_{i}[l_{i}+1]\right)\geq k}$ ist.[7]

algorithm msSelect(S : Array of sorted Sequences [S_1,..,S_p], k : int) is
    for i = 1 to p do
 (l_i, r_i) = (0, |S_i|-1)

    while there exists i: l_i < r_i do
 //pick Pivot Element in S_j[l_j],..,S_j[r_j], chose random j uniformly
 v := pickPivot(S, l, r)
 for i = 1 to p do
     m_i = binarySearch(v, S_i[l_i, r_i]) //sequentially
 if m_1 + ... + m_p >= k then //m_1+ ... + m_p is the global rank of v
     r := m  //vector assignment
 else
     l := m

    return l

Für die Komplexitätsanalyse wurde das PRAM-Modell gewählt. Die p-fache Ausführung der binarySearch Methode hat eine Laufzeit in ${\displaystyle {\mathcal {O}}\left(p\log \left(n/p\right)\right)}$, falls die Daten über alle ${\displaystyle p}$ Prozessoren gleichverteilt anliegen. Die erwartete Rekursionstiefe beträgt wie im Quickselect Algorithmus ${\displaystyle {\mathcal {O}}\left(\log \left(\textstyle \sum _{i}|S_{i}|\right)\right)={\mathcal {O}}(\log(n))}$. Somit ist die gesamte erwartete Laufzeit ${\displaystyle {\mathcal {O}}\left(p\log(n/p)\log(n)\right)}$.

Angewandt auf den parallelen Mehrwege-Mergesort muss die msSelect Methode parallel ausgeführt werden, um alle Trennelemente vom Rang ${\textstyle i{\frac {n}{p}}}$ gleichzeitig zu finden. Dies kann anschließend verwendet werden, um jede Folge in ${\displaystyle p}$ Teile zu zerschneiden. Es ergibt sich die gleiche Gesamtlaufzeit ${\displaystyle {\mathcal {O}}\left(p\,\log(n/p)\log(n)\right)}$.

Pseudocode

Hier i​st der komplette Pseudocode für d​en parallelen Mehrwege-Mergesort. Dabei w​ird eine Barriere-Synchronisation v​or und n​ach der Trennelementbestimmung angenommen, sodass j​eder Prozessor s​eine Trennelemente u​nd die Partitionierung seiner Sequenz richtig berechnen kann.

/**
 * d: Unsorted Array of Elements
 * n: Number of Elements
 * p: Number of Processors
 * return Sorted Array
 */
algorithm parallelMultiwayMergesort(d : Array, n : int, p : int) is
    o := new Array[0, n]                         // the output array
    for i = 1 to p do in parallel                // each processor in parallel
        S_i := d[(i-1) * n/p, i * n/p]           // Sequence of length n/p
 sort(S_i)                                // sort locally
        synch
 v_i := msSelect([S_1,...,S_p], i * n/p)          // element with global rank i * n/p
        synch
 (S_i,1 ,..., S_i,p) := sequence_partitioning(si, v_1, ..., v_p) // split s_i into subsequences

 o[(i-1) * n/p, i * n/p] := kWayMerge(s_1,i, ..., s_p,i)  // merge and assign to output array

    return o

Analyse

Zunächst sortiert jeder Prozessor die zugewiesenen ${\displaystyle n/p}$ Elemente lokal mit einem vergleichsbasierten Sortieralgorithmus der Komplexität ${\displaystyle {\mathcal {O}}\left(n/p\;\log(n/p)\right)}$. Anschließend können die Trennelemente in Zeit ${\displaystyle {\mathcal {O}}\left(p\,\log(n/p)\log(n)\right)}$ bestimmt werden. Schließlich müssen jede Gruppe von ${\displaystyle p}$ Teilstücken gleichzeitig von jedem Prozessor zusammen gemischt werden. Dies hat eine Laufzeit von ${\displaystyle {\mathcal {O}}(\log(p)\;n/p)}$, indem ein sequentieller k-Wege Mischalgorithmus verwendet wird. Somit ergibt sich eine Gesamtlaufzeit von

${\displaystyle {\mathcal {O}}\left({\frac {n}{p}}\log \left({\frac {n}{p}}\right)+p\log \left({\frac {n}{p}}\right)\log(n)+{\frac {n}{p}}\log(p)\right)}$.

Praktische Anpassung und Anwendung

Der Mehrwege-Mergesort Algorithmus i​st durch s​eine hohe Parallelität, w​as den Einsatz vieler Prozessoren ermöglicht, s​ehr skalierbar. Dies m​acht den Algorithmus z​u einem brauchbaren Kandidaten für d​as Sortieren großer Datenmengen, w​ie sie beispielsweise i​n Computer-Clustern verarbeitet werden. Da d​er Speicher i​n solchen Systemen i​n der Regel k​eine limitierende Ressource darstellt, i​st der Nachteil d​er Speicherkomplexität v​on Mergesort vernachlässigbar. Allerdings werden i​n solchen Systemen andere Faktoren wichtig, d​ie bei d​er Modellierung a​uf einer PRAM n​icht berücksichtigt werden. Hier s​ind unter anderem d​ie folgenden Aspekte z​u berücksichtigen: Die Speicherhierarchie, w​enn die Daten n​icht in d​en Cache d​er Prozessoren passen, o​der der Kommunikationsaufwand b​eim Datenaustausch zwischen d​en Prozessoren, d​er zu e​inem Engpass werden könnte, w​enn auf d​ie Daten n​icht mehr über d​en gemeinsamen Speicher zugegriffen werden kann.

Sanders et al. haben in ihrem Paper einen bulk synchronous parallel-Algorithmus für einen mehrstufigen Mehrwege-Mergesort vorgestellt, der ${\displaystyle p}$ Prozessoren in ${\displaystyle r}$ Gruppen der Größe ${\displaystyle p'}$ unterteilt. Alle Prozessoren sortieren zuerst lokal. Im Gegensatz zu einem einstufigen Mehrwege-Mergesort werden diese Sequenzen dann in ${\displaystyle r}$ Teile aufgeteilt und den entsprechenden Prozessorgruppen zugeordnet. Diese Schritte werden innerhalb dieser Gruppen rekursiv wiederholt. So wird die Kommunikation reduziert und insbesondere Probleme mit vielen kleinen Nachrichten vermieden. Die hierarchische Struktur des zugrundeliegenden realen Netzwerks (z. B. Racks, Cluster,...) kann zur Definition der Prozessorgruppen verwendet werden.[6]

Weitere Varianten

Mergesort war einer der ersten Sortieralgorithmen, bei dem ein optimaler Speedup erreicht wurde, wobei Richard Cole einen cleveren Subsampling-Algorithmus verwendete, um die O(1)-Zusammenführung sicherzustellen.[8] Andere ausgeklügelte parallele Sortieralgorithmen können die gleichen oder bessere Zeitschranken mit einer niedrigeren Konstante erreichen. David Powers beschrieb beispielsweise 1991 einen parallelisierten Quicksort (und einen verwandten Radixsort), der durch implizite Partitionierung in ${\displaystyle O(\log n)}$ Zeit auf einer CRCW-Parallel Random Access Machine (PRAM) mit ${\displaystyle n}$ Prozessoren arbeiten kann.[9] Powers zeigt ferner, dass eine Pipeline-Version von Batchers Bitonic Mergesort in ${\displaystyle O((\log n)^{2})}$ Zeit auf einem Butterfly-Sortiernetzwerk in der Praxis schneller ist als sein ${\displaystyle O(\log n)}$ Sortieralgorithmus auf einer PRAM, und er bietet eine detaillierte Diskussion der versteckten Overheads beim Vergleich, bei der Radix- und der Parallelsortierung.[10]

Sonstiges

Da Mergesort d​ie Startliste s​owie alle Zwischenlisten sequenziell abarbeitet, eignet e​r sich besonders z​ur Sortierung v​on verketteten Listen. Für Arrays w​ird normalerweise e​in temporäres Array derselben Länge d​es zu sortierenden Arrays a​ls Zwischenspeicher verwendet (das heißt Mergesort arbeitet normalerweise n​icht in-place, s. o.). Quicksort dagegen benötigt k​ein temporäres Array.

Die SGI-Implementierung d​er Standard Template Library (STL) verwendet d​en Mergesort a​ls Algorithmus z​ur stabilen Sortierung.[11]

Literatur

• Robert Sedgewick: Algorithmen. Pearson Studium, 2002, ISBN 3-8273-7032-9.

Weblinks

• Visualisierung und Tutorial für Mergesort, mit Darstellung der Rekursion
• Demonstration des Merge-Vorgangs (Java-Applet)

Einzelnachweise

1. Donald E. Knuth: The Art of Computer Programming. 2. Auflage. Vol. 3: Sorting and Searching. Addison-Wesley, 1998, S. 158.
2. h2database/h2database. In: GitHub. Abgerufen am 1. September 2016.
3. Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein: Introduction to algorithms. 3. Auflage. MIT Press, Cambridge, Mass. 2009, ISBN 978-0-262-27083-0.
4. Victor J. Duvanenko: Parallel Merge Sort. In: Dr. Dobb's Journal & blog. duvanenko.tech.blog and GitHub repo C++ implementation github.com
5. Peter Sanders, Johannes Singler: MCSTL:Multi-Core Standard Template Library. Practical Implementation of Parallel Algorithms for Shared-Memory Systems. 2008. Lecture Parallel algorithms Last visited 05.02.2020. http://algo2.iti.kit.edu/sanders/courses/paralg08/singler.pdf
6. dl.acm.org (Hrsg.): Practical Massively Parallel Sorting | Proceedings of the 27th ACM symposium on Parallelism in Algorithms and Architectures. doi:10.1145/2755573.2755595 (englisch, acm.org [abgerufen am 28. Februar 2020]).
7. Peter Sanders. 2019. Lecture Parallel algorithms Last visited 05.02.2020. http://algo2.iti.kit.edu/sanders/courses/paralg19/vorlesung.pdf
8. Richard Cole: Parallel Merge Sort. In: SIAM Journal on Computing. Band 17, Nr. 4, August 1988, ISSN 0097-5397, S. 770–785, doi:10.1137/0217049 (siam.org [abgerufen am 6. März 2020]).
9. David M. W. Powers: Parallelized Quicksort and Radixsort with Optimal Speedup. In: Proceedings of International Conference on Parallel Computing Technologies. Novosibirsk 1991.
10. David M. W. Powers: Parallel Unification: Practical Complexity, Australasian Computer Architecture Workshop, Flinders University, January 1995.
11. http://www.sgi.com/tech/stl/stable_sort.html stable_sort