Mittlere freie Weglänge

Die mittlere freie Weglänge $\lambda$ ist die Weglänge, die ein Teilchen (z. B. Atom, Molekül, Ion oder Elektron) in einem gegebenen Material im Durchschnitt zurücklegt, bevor es zum Stoß (irgendeiner Art) mit einem anderen Teilchen kommt. Hat ein Teilchenstrom in einem Material die mittlere freie Weglänge durchlaufen, so haben knapp 2/3 der Teilchen bereits einen Stoß ausgeführt, das übrige Drittel (genau ein Bruchteil 1/e) noch keinen.

Berechnung aus Wirkungsquerschnitt und Teilchendichte

Die mittlere freie Weglänge hängt mit der Teilchendichte $n$ (Anzahl der Teilchen pro Volumen) und dem totalen Wirkungsquerschnitt $\sigma$ zusammen:

\lambda ={\frac {1}{n\cdot \sigma }}

Anschaulich ist $\sigma$ die Größe der Zielscheibe, die ein Teilchen den anderen Teilchen für einen Stoß bietet. Nachdem es eine freie Weglänge $\lambda$ geflogen ist, hat es mit dieser Fläche das Volumen $\lambda \sigma =1/n$ überstrichen, das ist das Volumen, in dem sich durchschnittlich ein Teilchen befindet. Das Teilchen ist also im Durchschnitt einmal mit einem anderen Teilchen zusammengestoßen.

Abschätzung bei Gasen

Beim Stoß zweier kugelförmiger Teilchen mit gleichem Durchmesser $d$ ist $d$ auch der Abstand der Mittelpunkte, also der Radius des kreisförmigen geometrischen Wirkungsquerschnitts. Dieser ergibt sich zu

\sigma _{\text{geom}}=\pi \,d^{2}

Daraus folgt die geometrische mittlere freie Weglänge zu

\Rightarrow \lambda _{\text{geom}}={\frac {1}{\pi \,n\,d^{2}}}

Die oben gegebene Deutung gilt, wenn die Stoßpartner des fliegenden Teilchens in Ruhe sind.

Wenn sich aber alle Teilchen ungeordnet bewegen (d. h. auch die Stoßpartner des fliegenden Teilchens), führen Gleichgewichtsbetrachtungen unter Annahme einer Maxwellschen Geschwindigkeitsverteilung zu einer freien Weglänge, die um den Faktor ${\tfrac {1}{\sqrt {2}}}$ kürzer ist:[1]

\lambda ={\frac {1}{{\sqrt {2}}\,\pi \,n\,d^{2}}}

Definition für zwei Arten von Teilchen

In einem Raumbereich, der zwei Arten von Teilchen enthält, sind drei Arten von Stößen möglich:

zwei Teilchen vom Typ 1 stoßen aneinander
zwei Teilchen vom Typ 2 stoßen aneinander
am Stoß sind ein Teilchen vom Typ 1 und ein Teilchen vom Typ 2 beteiligt.

Die Teilchendichten der Teilchenarten seien $n_{1}$ bzw. $n_{2}$ und die Wirkungsquerschnitte $\sigma _{1}$ , $\sigma _{2}$ und $\sigma _{12}$ .

Die mittleren freien Weglängen für Stöße von Teilchen jeweils an ihresgleichen sind schon mit obiger Formel definiert:

\lambda _{1}={\frac {1}{n_{1}\cdot \sigma _{1}}}

bzw.

\lambda _{2}={\frac {1}{n_{2}\cdot \sigma _{2}}}

Entsprechend definiert man die mittlere freie Weglänge[2] eines Teilchens vom Typ 2 im Medium vom Typ 1:

\lambda _{21}={\frac {1}{n_{1}\cdot \sigma _{12}}}

bzw. analog $\lambda _{12}$ beim Stoß eines Teilchens vom Typ 1 im Medium vom Typ 2:

\lambda _{12}={\frac {1}{n_{2}\cdot \sigma _{12}}}

wobei in beiden Fällen der Wirkungsquerschnitt $\sigma _{12}$ gleich ist.

Der Wirkungsquerschnitt und die mittlere freie Weglänge zweier unterschiedlicher Teilchen werden meist ohne Index oder andere Auszeichnungszeichen geschrieben, also $\sigma =\sigma _{12}$ und $\lambda =\lambda _{21}$ :

\lambda ={\frac {1}{n_{1}\cdot \sigma }}

Der Index der Anzahldichte $n_{1}$ wird in der Regel ebenfalls weggelassen, wenn es nur um die mittlere freie Weglänge von Teilchen in irgendeinem Medium mit Teilchen vom Typ 1 geht. Dann scheinen die eingangs dieses Artikels gegebene Definition der mittleren freien Weglänge und die zuletzt gegebene Gleichung formelmäßig gleich zu sein (und werden deshalb auch manchmal verwechselt). Die Anzahldichten der Teilchen $n$ und $n_{1}$ sind in Wirklichkeit aber unterschiedliche Größen: bei $n$ handelt es sich um die Anzahldichte der Teilchen von nur einem Typ, bei $n_{1}$ aber um die Anzahldichte der Teilchen des Mediums.

Ähnlich wie beim Billardspiel bewirkt der elastische Stoß zweier Teilchen Richtungsänderungen beider Teilchen, allerdings, im Unterschied zum Billardspiel, im dreidimensionalen physikalischen Raum und mit Teilchen unterschiedlicher Größe. Häufig bedeutet ein Stoß zweier unterschiedlicher Teilchenarten auch, dass sie eine Reaktion miteinander eingehen. Sind die Stoßpartner zum Beispiel zwei Atome, kann ein Molekül gebildet werden, sind die Stoßpartner ein Neutron und ein Atomkern, kann ein anderes Nuklid entstehen oder ein Atomkern gespalten werden.

Implizit gehen wir davon aus, dass beide Stoßpartner Teilchen eines Gases sind, denn nur dort können sich beide Stoßpartner frei bewegen, was überhaupt erst nahelegt, von einer freien Weglänge zu sprechen. Es gibt aber auch Stöße und mittlere freie Weglängen, wenn ein Stoßpartner ein Teilchen eines Festkörpers oder einer Flüssigkeit ist (Teilchen vom Typ 1), und sich nur der zweite Stoßpartner wie ein Teilchen eines Gases verhält (Teilchen vom Typ 2). Dabei sind in der Regel Stöße von Teilchen vom Typ 1 mit Teilchen vom Typ 2 von Interesse (und nicht Stöße der beiden jeweiligen Teilchen-Typen mit ihresgleichen).

Abschätzung für den Stoß von zwei Arten von Teilchen

Der geometrische Wirkungsquerschnitt beim elastischen Stoß zweier starrer Kugeln mit den Radien $r_{1}$ bzw. $r_{2}$ ist

\sigma _{\text{geom}}=\pi \,(r_{1}+r_{2})^{2}

Damit wird die geometrische mittlere freie Weglänge:

\Rightarrow \lambda _{\text{geom}}={\frac {1}{\pi \,n_{1}\,(r_{1}+r_{2})^{2}}}

Der geometrische Wirkungsquerschnitt und damit die geometrische mittlere freie Weglänge der elastischen Streuung hängen also nicht von den kinetischen Energien der Kugeln ab. Reale Wirkungsquerschnitte und damit die mittleren freien Weglängen können dagegen stark von der kinetischen Energie der Stoßpartner abhängen und sind folglich nicht unbedingt durch das o. g. einfache geometrische Modell zu berechnen. Auch im Fall realer Wirkungsquerschnitte kann es jedoch hilfreich sein, den geometrischen Wirkungsquerschnitt als Bezugsgröße zu verwenden, in der Art: der reale Wirkungsquerschnitt ist 10-mal größer als der geometrische, dann ist die reale mittlere freie Weglänge nur ein Zehntel der geometrischen.

Stöße von Neutronen und Atomkernen

Stöße von Neutronen und Atomkernen sind (gegenwärtig) der wichtigste Fall in der Physik für Stöße von zwei Arten von Teilchen, sie prägen die Reaktorphysik.

Wenn in der Reaktorphysik von mittlerer freier Weglänge die Rede ist, ist stets die zweite Definition dieser Größe gemeint, also die mittlere freie Weglänge von Neutronen in Materie. Dabei bewegen sich freie Neutronen (Teilchen vom Typ 2 mit einer Teilchendichte $n_{2}$ ) in einem Festkörper oder einer Flüssigkeit („Wirtsmedium“) i. allg. so chaotisch wie Moleküle in einem Gas. Wir nehmen an, das Wirtsmedium bestehe aus nur einer Teilchen- bzw. einer Atomart (Teilchen von Typ 1), man denke etwa an Graphitatome. Da jedes Atom nur einen Atomkern besitzt, ist die Teilchendichte $n_{1}$ der Atome gleich der ihrer Atomkerne.

Der Kehrwert der mittleren freien Weglänge diese Typs ist unter dem Namen Makroskopischer Wirkungsquerschnitt eine der wichtigsten Größen der Reaktorphysik:

\Sigma ={\frac {1}{\lambda }}=n_{1}\cdot \sigma

Wirkungsquerschnitte von Kernreaktionen hängen extrem stark von der Energie ab und sind somit auch nicht mehr geometrisch zu erklären. Nur im Fall der elastischen Streuung von Neutronen an den Atomkernen gebräuchlicher Moderatoren führt das oben angegebene geometrische Modell auf mittlere freie Weglängen, die in der Größenordnung der gemessenen Werte liegen; dies zumindest für Neutronen mit kinetischen Energien in einem gewissen mittleren Intervall.

Neutronen untereinander stoßen sich auch. Dies ist ein Fall für die erste Definition der mittleren freien Weglänge. Die Anzahldichte der Neutronen ist selbst im Hochflussreaktor vergleichsweise gering. Klein ist auch der Wirkungsquerschnitt für den Stoß zweier Neutronen. Deshalb wird vermutlich in keinem Lehrbuch der Reaktor- oder Neutronenphysik die mittlere freie Weglänge für diesen Typ von Stoß auch nur erwähnt.

Atomkerne untereinander können sich nicht stoßen. Selbst im Fall, dass die Neutronen sich in Helium-Gas bewegen, wie im Hochtemperaturreaktor, stoßen allenfalls Helium-Atome aufeinander. Allerdings lässt sich, falls erforderlich, die mittlere freie Weglänge für solche Atomstöße mit der o. g. ersten Definitionsformel und dem geometrischen Wirkungsquerschnitt berechnen, der denjenigen der Atomkerne um Größenordnungen übertrifft.

Beispiele

Gasmoleküle

Die mittlere freie Weglänge eines Gasmoleküls beträgt in Luft unter Standardbedingungen etwa 68 Nanometer.

Nachfolgende Tabelle listet ungefähre Zahlen für freie Weglängen für Gasmoleküle bei verschiedenen Drücken auf:

Druckbereich	Druck in hPa	Teilchendichte $n$ in Moleküle pro cm³	mittlere freie Weglänge $\lambda$
Umgebungsdruck	1013	2,7·10¹⁹	68 nm
Grobvakuum	300 … 1	10¹⁹ … 10¹⁶	0,1 … 100 μm
Feinvakuum	1 … 10⁻³	10¹⁶ … 10¹³	0,1 … 100 mm
Hochvakuum (HV)	10⁻³ … 10⁻⁷	10¹³ … 10⁹	10 cm … 1 km
Ultrahochvakuum (UHV)	10⁻⁷ … 10⁻¹²	10⁹ … 10⁴	1 km … 10⁵ km
extr. Ultrahochv. (XHV)	<10⁻¹²	<10⁴	>10⁵ km

Elektronen

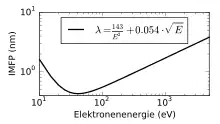
Universelle Kurve für die inelastische mittlere freie Weglänge von Elektronen in Elementen basierend auf Gleichung (5) in [3]

Die mittlere freie Weglänge freier Elektronen ist wichtig bei Anwendungen von Elektronenstrahlen im Vakuum (z. B. bei bestimmten oberflächensensitiven analytischen Methoden oder in Braunschen Röhren). Sie hängt ab von der kinetischen Energie des Elektrons.

Die inelastische freie Weglänge im Festkörper kann für die meisten Metalle mit einer „Universellen Kurve“ abgeschätzt werden (s. Abb.):[3] bei Energien um 100 eV ist sie für die meisten Metalle am geringsten, da hier Prozesse im Festkörper angeregt werden können, z. B. Plasmonen; bei höheren und niedrigeren Energien sind die mittleren freien Weglängen im Festkörper größer. Der Wirkungsquerschnitt für elastische Stöße ist meist kleiner als der für inelastische Stöße,[4] damit ist bei gleicher Teilchendichte die elastische freie Weglänge größer als die inelastische.

In gasförmigen Isolierstoffen (z. B. Schwefelhexafluorid) beeinflusst die mittlere freie Weglänge die elektrische Durchschlagfestigkeit.

Für Elektronen im Impulsraum (siehe Fermi-Kugel) betrachtet man statt der Weglänge die mittlere freie Flugzeit.

Einzelnachweise

William C. Hinds: Aerosol Technology: Properties, Behavior, and Measurement of Airborne Particles. Wiley-Interscience, New York 1999, ISBN 0-471-19410-7
Paul Reuss: Neutron physics. EDP Sciences, Les Ulis, France 2008, ISBN 978-2-7598-0041-4, S. xxvi, 669., S. 50
M. P. Seah, W. A. Dench: Quantitative electron spectroscopy of surfaces: A standard data base for electron inelastic mean free paths in solids. In: Surface and Interface Analysis. 1, 1979, S. 2, doi:10.1002/sia.740010103.
Wolfgang S. M. Werner: Electron transport in solids for quantitative surface analysis. In: Surface and Interface Analysis. 31, 2001, S. 141, doi:10.1002/sia.973.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] William C. Hinds: Aerosol Technology: Properties, Behavior, and Measurement of Airborne Particles. Wiley-Interscience, New York 1999, ISBN 0-471-19410-7

[2] Paul Reuss: Neutron physics. EDP Sciences, Les Ulis, France 2008, ISBN 978-2-7598-0041-4, S. xxvi, 669., S. 50

[Seah-3] M. P. Seah, W. A. Dench: Quantitative electron spectroscopy of surfaces: A standard data base for electron inelastic mean free paths in solids. In: Surface and Interface Analysis. 1, 1979, S. 2, doi:10.1002/sia.740010103.

[Werner-4] Wolfgang S. M. Werner: Electron transport in solids for quantitative surface analysis. In: Surface and Interface Analysis. 31, 2001, S. 141, doi:10.1002/sia.973.