Außenballistik

Die Außenballistik untersucht die Bahn antriebsloser, ungelenkter ballistischer Geschosse. Die Aussagen der Außenballistik gelten

für Geschosse aus Rohrwaffen,
für ballistische Raketengeschosse (Kurz- bis Mittelstreckenraketen) nach dem Brennschluss
und für die Flugbahn von Bomben.

Die Bahn angetriebener oder gelenkter Geschosse, Raketen und Bomben wird in der Raketenballistik behandelt.

Die vier Hauptaufgaben der Außenballistik sind:

Ermittlung der Geschossbahn nach dem klassischen Bahnmodell unter meteorologischen und ballistischen Normalbedingungen
Untersuchungen der Starrkörperbewegungen des Geschosses und deren Einflüsse
Berücksichtigung der Abweichungen von den Normalbedingungen, also die Störrechnung
Ermittlung von Schusstafeln und Bombenwurftafeln

Grundlagen

Das einfachste Modell der Außenballistik beschreibt die Bewegung eines Massepunktes im Schwerefeld der Erde unter Vernachlässigung der Erdkrümmung und des Luftwiderstandes auf der Wurfparabel. Dieses Modell wird als parabolisches Bahnmodell bezeichnet. Seine Aussagen werden häufig als Ausgangswerte für Näherungsverfahren schwierigerer Modelle verwendet. Außerdem beschreibt dieses Modell recht gut die Bahnen langsamer Geschosse und Bomben.

Eine Verbesserung des Modells berücksichtigt den Luftwiderstand und die Abhängigkeit der Fallbeschleunigung von der geodätischen Höhe, jedoch nicht die Starrkörperbewegungen des Geschosses. Das so erhaltene Modell heißt Klassisches Bahnmodell. Es ist für viele Zwecke, etwa für die Feuerleitung im Allgemeinen ausreichend.

Die beiden Modelle zählen zu den Modellen mit drei Freiheitsgraden.

die Flugzeit (t₁ und t₂) beim horizontalen Schuss ist gleich der Fallzeit t₃ aus der Höhe der Mündung s

Abgefeuerte Geschosse unterliegen auf ihrer Bahn der Fallbeschleunigung, wodurch sich ihre Bewegung aus der Vorwärtsbewegung und der Fallbewegung zusammensetzt. Die Wirkung der beiden Komponenten ist beim waagerechten Schuss ohne Berücksichtigung des Luftwiderstandes anschaulich darstellbar. Die Bewegungen entlang der Horizontalen und der Vertikalen können hierbei entsprechend dem Superpositionsprinzip getrennt beobachtet werden.

Schuss mit Geländewinkel

Änderung der Schussweite bei Schießen mit Geländewinkel

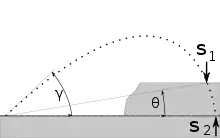
Liegt das Ziel auf einer anderen Höhe als der Abschusspunkt, muss bei gleicher horizontaler Distanz der Abschusswinkel angepasst werden. Bei höher liegenden Zielen muss der Aufsatzwinkel bzw. die Anfangsgeschwindigkeit vergrößert werden, bei tiefer liegenden Zielen verringert.
In der Illustration ist $\gamma$ der Abschusswinkel ausgehend von der Horizontalen, $\theta$ der Winkel zum Ziel. Die Schussweite $s_{1}$ im luftleeren Raum ergibt sich aus[1]:
$s_{1}={\frac {2\cdot {v_{0}}^{2}}{g}}\cdot {\frac {\cos \theta \cdot \sin \left(\theta -\gamma \right)}{\cos \left(\gamma \right)^{2}}}$

Streuung

Hauptartikel: Streuung (Ballistik)

Auch bei scheinbar gleichen Ausgangsbedingungen ist es sehr unwahrscheinlich, dass eine Waffe mit aufeinander folgenden Schüssen den exakt gleichen Punkt trifft. Durch geringe, nicht vermeidbare Variationen der Ausgangsparameter von Waffe und Munition sowie der Luft bewegen sich die Geschosse bei jedem Schuss auf einer etwas abweichenden Bahn. Das Maß dieser Abweichung ist die Streuung.

Geschossbahnen in der Atmosphäre

Modellatmosphäre und Standardatmosphäre

Für die Berechnung der Bahnelemente eines Geschosses sind Kenntnisse über die Physik der Atmosphäre notwendig. Grundlage aller aerodynamischen Berechnungen in der Ballistik ist eine Modellatmosphäre, für die die Höhenabhängigkeit ihrer Eigenschaften mathematisch formuliert wird. Die mathematische Beschreibung der Modellatmosphäre basiert auf den Daten der wissenschaftlichen Erforschung der Erdatmosphäre, wie sie seit langem mit Luft- und Raumfahrzeugen durchgeführt wird. Ziel ist es, für jede Höhe die Beziehungen und Abhängigkeiten der atmosphärischen Parameter durch mathematische Formeln darstellbar zu machen. Für die Ballistik sind Parameter von Interesse, die den Luftwiderstand eines Geschosses mitbestimmen. Das sind Luftdichte und Luftdruck sowie die Schallgeschwindigkeit und der Einfluss der Luftfeuchte auf diese Größen. Bei hohen Bahnen ist auch die Abnahme der Fallbeschleunigung mit zunehmender Höhe zu berücksichtigen.

Aufbauend auf den Gesetzmäßigkeiten der Modellatmosphäre wird eine Standardatmosphäre festgelegt, für die diese Gesetzmäßigkeiten auf konkrete Zahlenwerte angewendet werden. Für die Standardatmosphäre werden in der Regel die Zahlenwerte der atmosphärischen Parameter in Bodennähe festgelegt und deren Höhenabhängigkeit gemäß den Vorgaben der Modellatmosphäre ermittelt. Die Parameter umfassen:

Lufttemperatur am Boden
Luftdruck am Boden
Luftdichte am Boden (die sich aus ihnen und der Luftzusammensetzung ergibt)
Schallgeschwindigkeit am Boden
Fallbeschleunigung am Boden
Adiabatenexponent am Boden
Molare Masse der Luft am Boden
dynamische Zähigkeit der Luft am Boden
mittlere freie Weglänge der Luftmoleküle am Boden
Erdradius

Zur Berechnung der Luftdichte werden die 1952 von der ICAO eingeführten Modelle für die Normalatmosphäre benutzt,[1] die es erlauben, sowohl den aktuellen Luftdruck sowie die Höhe über mittlerem Meeresniveau entsprechend in den Berechnungen zu berücksichtigen.

Es werden international verschiedene Standardatmosphären für ballistische Berechnungen genutzt, wobei auch an bestimmte Einsatzfelder und klimatische Bedingungen angepasste artilleristische Normalatmosphären verwendet werden, die zum Teil einige der Parameter aus praktischen Gründen vernachlässigen.

Maximale Schussweite

Für schnelle, weitreichende Geschosse ergeben sich vor allem durch den Luftwiderstand erhebliche Abweichungen von der Wurfparabel. Ohne Luftwiderstand würde ein unter einem Winkel von 45° mit einer Mündungsgeschwindigkeit von 700 m/s abgefeuertes Geschoss etwa 50 km weit fliegen. Leichte Geschosse, wie etwa aus Büchsen, erreichen durch die Einwirkung des Luftwiderstands jedoch nur eine maximale Flugweite von 3 bis 4 km. Durch die starke Abbremsung erreichen Büchsengeschosse ihre maximale Schussweite nicht beim theoretisch optimalen Abschusswinkel von 45°, sondern bei etwa 30 bis 35°,[2] und die noch leichteren Schrotkugeln von Flinten erreichen ihre maximale Flugweite bei Abschusswinkeln von 20 bis 30°.[3]

Die Geschosse weitreichender Geschütze durchqueren auf ihrer Bahn hohe Atmosphärenschichten, in denen der Luftwiderstand durch die geringere Luftdichte deutlich niedriger ist als in Bodennähe. Der Aufsatzwinkel des Geschützes muss in diesem Fall über 45° liegen, um zu erreichen, dass die Geschosse beim Erreichen der Höhenbereiche niedrigeren Luftwiderstands einen Winkel von 45° aufweisen, was nach dem parabolischen Modell optimal für das Erzielen einer maximalen Schussweite ist. Für reichweitenoptimierte Geschosse mit einer Mündungsgeschwindigkeit von 1000 bis 1500 m/s liegt der Abschusswinkel bei 50 bis 55°. Zwischen Anfangsgeschwindigkeit und optimalem Abschusswinkel besteht dabei ein komplizierter nichtlinearer Zusammenhang, so würde bei einer weiteren Steigerung der Anfangsgeschwindigkeit der Winkel für eine maximale Reichweite wieder sinken, da die dichten Luftschichten schneller durchflogen werden.[2]

Aerodynamischer Einfluss auf Geschosse

Ein abgefeuertes Geschoss wird in der Atmosphäre von Luft umströmt, was zur Wirkung verschiedener Kräfte führt, die die Bahn des Geschosses beeinflussen. In erster Linie ist das der Luftwiderstand, der das Geschoss abbremst und zu einer Abweichung der Bahn von der Wurfparabel führt.

Geschosse wie Raketen, Pfeilgeschosse oder Flintenlaufgeschosse werden aerodynamisch stabilisiert. Bei diesen Geschossen liegt der aerodynamische Druckpunkt hinter dem Masseschwerpunkt. Kippen diese Geschosse in der Längsachse, werden sie durch den hinter dem Schwerpunkt liegenden Druckpunkt wieder ausgerichtet. Diese Geschosse besitzen Leitwerke oder ein leichtes Heck, wodurch der Druckpunkt nach hinten verschoben wird.

Bei den meisten Geschossen mit Drallstabilisierung liegt der Druckpunkt vor dem Masseschwerpunkt. Durch diese aerodynamische Instabilität entsteht ein Kippmoment nach hinten, so dass sie sich ohne Drall nach dem Verlassen des Laufes überschlagen würden. Durch den Drall werden sie ähnlich einem auf der Spitze stehenden Kreisel durch Kreiselkräfte stabilisiert.

Diese Geschosse verlassen den Lauf nicht exakt in Flugrichtung ausgerichtet, sondern mit einem geringen Anstellwinkel. Folge des Anstellwinkels sind Kräfte, die quer zur Luftwiderstandskraft wirken. Zum einen ist das eine Auftriebskraft, die in der Ebene des Anstellwinkels wirkt, zum anderen erzeugt der Drall durch den Magnus-Effekt eine Querkraft, die senkrecht zu dieser Ebene wirkt. Die Auftriebskraft wirkt immer in Richtung des Anstellwinkels, kann also bei entsprechender Ausrichtung des Anstellwinkels auch nach unten gerichtet sein. Die Querkräfte bewirken eine seitliche Ablenkung des Geschosses in Drallrichtung, also nach rechts bei Rechtsdrall. Bei Artilleriegeschossen können die Querkräfte zu einer seitlichen Beschleunigung von 0,15 bis 0,25 m/s² führen, wobei dieser Wert mit wachsender Flugdauer abnimmt.[4]

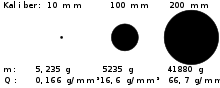
überproportionaler Anstieg von Masse m und Querschnittsbelastung Q bei Erhöhung des Kalibers

Obwohl aus Geschützen abgefeuerte schwere Geschosse den gleichen aerodynamischen Einflüssen unterliegen und in der Regel mit Handfeuerwaffen vergleichbare Mündungsgeschwindigkeiten aufweisen, erreichen sie deutlich größere maximale Schussweiten von etwa 20 bis 40 km. Die Ursache hierfür liegt in der Querschnittsbelastung der Geschosse. Steigt das Kaliber eines Geschosses, steigt die Querschnittsfläche quadratisch zum Durchmesser. Gleichzeitig steigt jedoch das Volumen des Geschosses proportional zur dritten Potenz des Durchmessers, und damit steigt seine Masse ebenfalls proportional zur dritten Potenz. Bei gleicher Geschossform und -dichte bewirkt eine Verzehnfachung des Kalibers eine Vertausendfachung der Masse und eine Verhundertfachung der Querschnittsbelastung. Dadurch, dass die auf die Querschnittsfläche wirkende Gewichtskraft stärker steigt als der durch die Kalibererhöhung steigende Luftwiderstand, wird das Geschoss langsamer abgebremst.

Neben der Querschnittsbelastung ist der Luftwiderstandsbeiwert ( $c_{W}$ -Wert) entscheidend für die Reichweite eines Geschosses. Geschosse moderner Waffen erreichen Geschwindigkeiten vom hohen Unterschall- bis in den hohen Überschallbereich. Vor allem im Bereich der Schallgeschwindigkeit (um Mach 1) steigt der $c_{W}$ -Wert durch die Entstehung einer Bugwelle aus komprimierter Luft steil an (Wellenwiderstand). Dieser Bereich komprimierter Luft erzeugt einen Überschallknall. Bei höheren Geschwindigkeiten nimmt der $c_{W}$ -Wert wieder ab, wobei der Anteil des Wellenwiderstands am Gesamtwiderstand bis über 70 % liegt. Für die Berechnung des Luftwiderstandes eines Überschallgeschosses werden die $c_{W}$ -Werte der Geschossspitze, des Geschosskörpers, des Heckkonus’ und des Hecksoges getrennt betrachtet und addiert.[5]

Die Abhängigkeit des $c_{W}$ -Wertes von der Geschwindigkeit ( $c_{W}$ als Funktion von $v$ ) muss bei der Berechnung der Bahnelemente eines Geschosses berücksichtigt werden. In der Regel wird diese Funktion nicht für jeden Geschosstyp neu ermittelt, sondern ein Standard-Luftwiderstandsgesetz verwendet, das dann mittels eines Formkoeffizienten für den jeweiligen Geschosstyp korrigiert wird.

Für den Überschallbereich ausgelegte Geschosse wie moderne Langgeschosse bzw. Artilleriegranaten besitzen oft ogival geformte Spitzen. Die ogivale Spitze ist für Überschallflugkörper am strömungsgünstigsten. Ein ogivales Heck ist bei Rohrwaffen konstruktiv nicht umsetzbar, so dass das Heck meist nur als Kegelstumpf (Heckkonus) ausgeformt ist, um die Abbremsung durch den Hecksog zu vermindern.

Für die Berechnung der Reichweite wird aus Luftwiderstandsbeiwert und Gewicht eines Geschosses auch ein Ballistischer Koeffizient ermittelt. In der Ballistik gibt es mehrere Definitionen des Ballistischen Koeffizienten, was bei Berechnungen, die auf diesem Wert aufbauen, berücksichtigt werden muss.[6]

Einfluss auf Geschossbahnen

Eine Geschossbahn in der Atmosphäre besitzt bei Abschusswinkeln zwischen 0 und 90° ebenfalls eine vertikale und eine horizontale Komponente.

horizontale Komponente u und vertikale Komponente w der Geschossbewegung (Weg s und Höhe h)

Die Geschwindigkeitskomponenten $u$ und $w$ errechnen sich aus dem Abschusswinkel ϑ und der Geschwindigkeit v:
$u=v\cdot \cos \vartheta$
$w=v\cdot \sin \vartheta$
Während beim Schuss im Vakuum die horizontale Komponente der Geschwindigkeit konstant bleibt (gleichförmige Bewegung), sinkt sie beim Schuss unter Einfluss des Luftwiderstandes monoton ab, auch wenn die vertikale Geschwindigkeitskomponente nach dem Geschwindigkeitsminimum wieder zunimmt. Der fallende Abschnitt der Geschossbahn ist daher grundsätzlich steiler als der steigende. Der horizontale Geschwindigkeitsanteil folgt dabei der Geschwindigkeit eines waagerecht fliegenden Geschosses, dessen Geschwindigkeit durch den Luftwiderstand ständig abnimmt. Analog folgt der Verlauf der vertikalen Geschwindigkeitskomponente dem eines Projektils, das mit dem anteiligen Geschwindigkeitswert der vertikalen Komponente senkrecht nach oben geschossen wurde.

Nach Überschreiten des Bahngipfels können Geschosse eine Grenzgeschwindigkeit erreichen, wobei sich ein Gleichgewicht zwischen der Gewichtskraft und der Luftwiderstandskraft einstellt.

Bei Flugbahnen im Vakuum tritt das Minimum der Geschossgeschwindigkeit im Bahngipfel auf, bei Flugbahnen in Luft erst nach dem Bahngipfel, da die Abbremsung durch den Luftwiderstand zunächst die Geschwindigkeitszunahme durch die Fallbeschleunigung überwiegt. Bei flachen Bahnen kann das Geschoss darum das Ziel vor Eintreten dieses Minimums erreichen, so dass die Geschossgeschwindigkeit bis zum Ziel ohne erneuten Anstieg nach dem Bahngipfel permanent sinkt.[7]

Für genauere Berechnungen werden in der Ballistik weitere Werte genutzt und verschiedene Störfaktoren genauer betrachtet.[8]

Diese Störfaktoren sind vor allem Änderungen der atmosphärischen Bodenwerte, Abweichungen der höhenabhängigen Verläufe (Gradienten) der atmosphärischen Parameter von der Normalatmosphäre, Windeinflüsse und auch Wettereinflüsse wie Regen oder Schneefall. Bei weitreichenden Bahnen muss der Einfluss der Erdkrümmung und der Erddrehung in die Berechnung einbezogen werden.

Für die Berechnung der Bahnabweichungen durch die atmosphärischen Störfaktoren existieren keine exakten mathematischen Modelle, so dass nur Näherungslösungen möglich sind. Bevor leistungsfähige computergestützte Feuerleitrechner zur Verfügung standen, wurden die Richtdaten der Geschütze über Schusstafeln ermittelt und korrigiert. Ausgehend von den festen Parametern Anfangsgeschwindigkeit, Abschusswinkel und einem Geschossparameter wie dem ballistischen Koeffizienten werden dabei abhängig von den auftretenden Abweichungen die Richtdaten aus den Schusstafeln entnommen.

Je größer die Schussweite ist, desto größeren Einfluss bekommt die Höhenabhängigkeit der atmosphärischen Parameter. Luftdruck, Luftdichte und Lufttemperatur und damit auch die Schallgeschwindigkeit verändern sich mit zunehmender Höhe. All diese Eigenschaften sind bestimmend für den Luftwiderstand eines Geschosses, und die Kenntnis ihres höhenabhängigen Verlaufes wesentlich für die Vorhersage der Flugbahnelemente. Daneben hat auch die Luftfeuchte Einfluss auf den Druckverlauf und die Schallgeschwindigkeit.

Oberhalb von etwa 90 km verändern sich die Eigenschaften der Atmosphäre durch die zunehmende mittlere freie Weglänge dahingehend, dass die Atmosphäre nicht mehr als ideales Gas wirkt und grundlegende Gesetze der Strömungslehre nicht mehr angewandt werden können. Betrachtungen zu Geschossbahnen in solchen Höhen sind vor allem Gegenstand der Raketenballistik.

Direktes Feuer und bestrichener Bereich

Der Bereich des direkten Feuers etwa von Flachfeuergeschützen liegt innerhalb der Entfernung, in der der Scheitelpunkt der Geschossbahn unter dem höchsten Punkt des Ziels liegt. In diesem Bereich haben äußere Störungen den geringsten Einfluss, so dass in der Praxis die Flugbahn des Geschosses mit ausreichender Näherung mit der Wurfparabel im Vakuum übereinstimmt.

Liegt der Scheitelpunkt höher als das Ziel, sind die Abschnitte der Geschossbahn, die mit dem Ziel auf gleicher Höhe liegen, der bestrichene Bereich.

Die Größe des Bereiches des direkten Feuers hängt von der Rasanz der Geschossbahn ab.

Bombenwurf

Horizontaler Abwurf

Beim Abwurf freifallender, ungelenkter Bomben aus Flugzeugen ist für ein Treffen des Ziels vor allem der Zeitpunkt des Ausklinkens der Bombe für die Treffsicherheit entscheidend. Dieser Zeitpunkt ist abhängig von der Höhe $h$ und der Fluggeschwindigkeit $v_{0}$ des Flugzeuges. Je schneller und höher das Flugzeug fliegt, in desto größerer Distanz vor dem Ziel muss die Bombe ausgeklinkt werden. Beim Abwurf aus dem Horizontalflug folgt die Falldauer $t_{F}$ unter Vernachlässigung des Luftwiderstandes aus dem Fallgesetz, $g$ ist die Fallbeschleunigung, die als konstant angenommen wird:

$t_{F}={\sqrt {\frac {2\cdot h}{g}}}$

Die Distanz $s_{D}$ , die die Bombe bis zum Auftreffen über dem Boden zurücklegt, ergibt sich in diesem Fall aus:

$s_{D}=v_{0}\cdot {\sqrt {\frac {2\cdot h}{g}}}$

Die Bombe muss in dieser Distanz vor dem Ziel abgeworfen werden.

Die Berechnung der Bahnelemente von Bomben kann vereinfacht werden, wenn als zusätzlicher Parameter $par$ das Verhältnis aus der potentiellen Energie $W_{p}$ und der kinetischen Energie $W_{k}$ der Bombe im Moment des Abwurfes ermittelt wird. Die Bombe mit der Masse $m$ befindet sich im Flugzeug in der Höhe $h$ über dem Boden. Die potentielle Energie ergibt sich aus:

$W_{p}=m\cdot g\cdot h$

Durch die Geschwindigkeit $v$ des Flugzeuges erhält die Bombe eine kinetische Energie:

$W_{k}={\frac {m\cdot v^{2}}{2}}$

Der Parameter $par$ ist der Quotient aus beiden Werten:

$par={\frac {W_{p}}{W_{k}}}$

Der Tangens des Auftreffwinkels $\vartheta _{Z}$ der Bombe bei Abwurf aus horizontalem Flug kann mit Hilfe dieses Parameters einfach ermittelt werden:

$\tan \vartheta _{Z}={\sqrt {par}}$

Bombenauslösung bei Vorhaltewinkel φ

Im Fall einer rein optischen Zielerfassung ermittelt der Bombenschütze nicht die Entfernung zum Ziel, in der er die Bombe auslösen muss, sondern misst den Winkel zwischen Flugzeug und dem Ziel, bis dieser Winkel dem der Höhe und Geschwindigkeit angemessenen Vorhaltewinkel $\phi$ entspricht. Der Tangens des Vorhaltewinkels ergibt sich aus:

$\tan {\varphi }={\frac {h}{s_{D}}}={\frac {h}{v_{0}}}\cdot {\sqrt {\frac {g}{2h}}}={\frac {1}{2}}{\sqrt {par}}$

Abwurf aus dem Steigflug

Bei einem Abwurf aus dem Steigflug mit dem Winkel $\vartheta _{0}$ ergeben sich umfangreichere Formeln.
Die Zeit $t_{G}$ vom Abwurf der Bombe bis zum Erreichen des Bahngipfels ergibt sich aus:
$t_{G}={\frac {v_{0}\cdot \sin {\vartheta _{0}}}{g}}$

Die Flugzeit $t_{F}$ ergibt sich aus:
$t_{F}=t_{g}\cdot \left(1+{\sqrt {1+{\frac {par}{\sin ^{2}\vartheta _{0}}}}}\right)$

Der Weg $s_{G}$ bis zum Bahngipfel ergibt sich aus:
$s_{G}={\frac {{v_{0}}^{2}}{2g}}\cdot \sin 2\vartheta _{0}$

Die horizontale Wurfdistanz $s_{D}$ ergibt sich aus:
$s_{D}=s_{G}\left(1+{\sqrt {1+{\frac {par}{\sin ^{2}\vartheta _{0}}}}}\right)$

Literatur

Hellmuth Molitz, Reinhold Strobel: Äußere Ballistik. Springer 1984, ISBN 3-540-02943-5.
Felix Poklukar: Modelle für Außenballistik – Zielballistik, HTLB Ferlach, 2005 (PDF, 303 kB) (Memento vom 20. März 2018 im Internet Archive)
Bernd Brinkmann, Burkhard Madea: Handbuch gerichtliche Medizin, Band 1. (Kapitel 9.6 Außenballistik) ISBN 978-3-540-00259-8.
Carl Cranz, Ballistik, Kapitel 18 (1903) in der Encyklopädie der mathematischen Wissenschaften mit Einschluss ihrer Anwendungen Uni-Göttingen, online einsehbar

Siehe auch

Weblinks

Commons: Artillerieballistik – Sammlung von Bildern

Commons: Außenballistik verschiedener Patronen – Sammlung von Bildern

Einzelnachweise

Felix Poklukar:Modelle für Außenballistik – Zielballistik, HTLB Ferlach, 2005 (PDF, 303 kB) (Memento vom 20. März 2018 im Internet Archive), eingesehen am 11. Dezember 2009
Günter Hauck: Äußere Ballistik. 1. Auflage. Militärverlag der DDR, 1972.
Willi Barthold: Jagdwaffenkunde. VEB Verlag Technik, Berlin 1969, bearbeitete Auflage 1979, S. 182.
G. Hauck: Äußere Ballistik. 1. Auflage. Militärverlag der DDR, 1972, S. 513.
G. Hauck: Äußere Ballistik. 1. Auflage. Militärverlag der DDR, 1972, S. 133.
G. Hauck: Äußere Ballistik. 1. Auflage. Militärverlag der DDR, 1972, S. 140.
G. Hauck: Äußere Ballistik. 1. Auflage. Militärverlag der DDR, 1972, S. 195 ff.
Bernd Brinkmann, Burkhard Madea: Handbuch gerichtliche Medizin, Band 1. Kapitel 9.6 Außenballistik, Seite 611, (eingesehen am 22. November 2009)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Nr.1-1] Felix Poklukar:Modelle für Außenballistik – Zielballistik, HTLB Ferlach, 2005 (PDF, 303 kB) (Memento vom 20. März 2018 im Internet Archive), eingesehen am 11. Dezember 2009

[Hauck,_Äußere_Ballistik-2] Günter Hauck: Äußere Ballistik. 1. Auflage. Militärverlag der DDR, 1972.

[3] Willi Barthold: Jagdwaffenkunde. VEB Verlag Technik, Berlin 1969, bearbeitete Auflage 1979, S. 182.

[4] G. Hauck: Äußere Ballistik. 1. Auflage. Militärverlag der DDR, 1972, S. 513.

[5] G. Hauck: Äußere Ballistik. 1. Auflage. Militärverlag der DDR, 1972, S. 133.

[6] G. Hauck: Äußere Ballistik. 1. Auflage. Militärverlag der DDR, 1972, S. 140.

[7] G. Hauck: Äußere Ballistik. 1. Auflage. Militärverlag der DDR, 1972, S. 195 ff.

[8] Bernd Brinkmann, Burkhard Madea: Handbuch gerichtliche Medizin, Band 1. Kapitel 9.6 Außenballistik, Seite 611, (eingesehen am 22. November 2009)