Achilles und die Schildkröte

Das Paradoxon von Achilles und der Schildkröte ist einer von mehreren bekannten Trugschlüssen, die dem griechischen Philosophen Zenon von Elea (5. Jh. v. Chr.) zugeschrieben werden, und eines von vier Paradoxa, die Aristoteles in seiner Abhandlung Physik beschreibt.

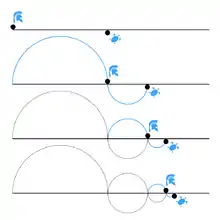
Grafische Veranschaulichung des Paradoxon

Paradoxon

Das Paradoxon handelt von einem Wettlauf zwischen dem für seine Schnelligkeit bekannten Achilles und einer sich langsam bewegenden Schildkröte. Beide starten zum selben Zeitpunkt, aber die Schildkröte erhält anfangs einen Vorsprung. Obwohl Achilles schneller ist, kann er sie niemals einholen.

Zenons Argument beruht auf der Annahme, dass Achilles zunächst den Punkt erreichen muss, an dem die Schildkröte gestartet ist. Bis zu diesem Zeitpunkt wird sich die Schildkröte, wenn auch nur um eine kleine Strecke, zu einem anderen Punkt vorwärts bewegt haben. Bis Achilles die Strecke zu diesem Punkt zurückgelegt hat, wird die Schildkröte zu einem anderen Punkt vorgerückt sein usw.

Lösung von Aristoteles

Das Achilles-Paradoxon verdeutlicht das Problem des Kontinuums. Aristoteles’ Lösung für dieses Problem bestand darin, die Segmente der Achillesbewegung als nur potentiell und nicht wirklich zu behandeln, da er sie nie durch Anhalten verwirklicht. In einer Vorwegnahme der modernen Maßtheorie argumentierte Aristoteles, dass eine Unendlichkeit von Unterteilungen einer Strecke, die endlich ist, nicht die Möglichkeit ausschließt, diese Strecke durchzulaufen, da die Unterteilungen nicht wirklich existieren, es sei denn, man tut etwas mit ihnen, in diesem Fall das Anhalten an ihnen.

Mathematische Lösung

Tatsächlich wird ein Schnellerer einen Langsameren aber immer einholen, sofern er dafür nur genügend Zeit hat. Die zum Einholen benötigte Zeit ist proportional zum Vorsprung und umgekehrt proportional zur Differenz der Geschwindigkeiten der beiden Läufer[Anm. 1] und bei gleichbleibendem Verhältnis dieser beiden Geschwindigkeiten umgekehrt proportional zu jeder derselben.[Anm. 2]

Ein geometrischer Beweis mittels des Strahlensatzes, der auch den Griechen möglich war. (Optimalerweise wählt man am Ursprung für Achilles einen 45°-Winkel.)

Schildkröte

Achilles

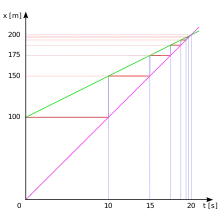
Zenons Trugschluss beruht auf zwei Fehlern:[1]

Er berücksichtigt nicht, dass eine unendliche Reihe eine endliche Summe haben kann.[Anm. 3][Anm. 4]
Der Weg, den Achilles von seinem Ausgangspunkt bis zum Zusammentreffen mit der Schildkröte zurücklegt, kann beliebig oft – formal unendlich oft – in Vorsprünge der Schildkröte unterteilt werden. Aus der Tatsache, dass diese Teilungshandlung beliebig oft vorgenommen werden kann, folgt aber nicht, dass die zu durchlaufende Strecke unendlich wäre[Anm. 5] oder dass unendlich viel Zeit erforderlich wäre, sie zurückzulegen.

Zenons Paradoxien

Es gibt unterschiedliche Ansichten darüber, was Zenon mit seinen „Paradoxien“ zeigen wollte. Häufig wird vermutet, dass sie die Eleatische These (siehe Parmenides von Elea) stützen sollten, der zufolge es in der Wirklichkeit keine Vielheit, sondern nur ein einziges unveränderliches und unzerstörbares Ganzes gebe, und dass die Alltagswahrnehmung von Vielfalt und Bewegung bloßer Schein sei. Sicher ist jedoch, dass diese antike Überlegung zur Begriffsbildung der Unendlichkeit beigetragen hat und auch heute noch als Lehrbeispiel verwendet wird.

Das Paradoxon ist nicht direkt überliefert, sondern findet sich in Aristoteles’ Physik[2][3] und Simplikios’ Kommentar[4] dazu.

Verwandte Paradoxa, die Zenon zugeschrieben werden, sind das Teilungsparadoxon und das Pfeil-Paradoxon. Inhaltlich nicht verwandt mit dem Zenonischen Paradox ist ein von Lewis Carroll in seinem kurzen Dialog What the Tortoise Said to Achilles[5] (Was die Schildkröte zu Achilles sagte) vorgestelltes Argument, mit dem er den Unterschied zwischen objekt- und metasprachlicher Implikation thematisiert und das gelegentlich als Carroll-Paradox bezeichnet wird.[6]

Siehe auch

Infinitesimalrechnung

Anmerkungen

Sei $t$ die Zeit, die vom Beginn des Rennens bis zu dem Zeitpunkt verstreicht, zu dem Achilles die Schildkröte einholt, $s$ der Weg, den Achilles während der Zeit $t$ zurücklegt, $s'$ der Weg, den die Schildkröte während der Zeit $t$ zurücklegt, $s_{0}$ der Vorsprung der Schildkröte zu Beginn des Rennens, $v_{a}$ die Geschwindigkeit Achilles’, $v_{s}$ die Geschwindigkeit der Schildkröte. Dann lässt sich t wie folgt berechnen:
$v_{a}\cdot t=s=s_{0}+s'=s_{0}+v_{s}\cdot t$ , also $s_{0}=v_{a}\cdot t-v_{s}\cdot t=(v_{a}-v_{s})\cdot t$ ; mit $v_{a}-v_{s}\neq 0$ folgt nach Division: $t={\frac {s_{0}}{v_{a}-v_{s}}}$ .
Letzteres zeigt die im Text behauptete Proportionalität der Zeit $t$ zum Vorsprung $s_{0}$ der Schildkröte und die umgekehrte Proportionalität von $t$ zur Geschwindigkeitsdifferenz $v_{a}-v_{s}$ .
(Mit $v_{a}\neq 0$ ) sei weiter $q={\frac {v_{s}}{v_{a}}}$ das Verhältnis der Geschwindigkeiten, sodass $v_{s}=q\cdot v_{a}$ , (mit $v_{s}\neq 0$ ) auch ${\frac {1}{v_{a}}}={\frac {q}{v_{s}}}$ . Wegen $v_{a}-v_{s}\neq 0$ ist $q\neq 1$ , und der Ausdruck für $t$ lässt sich weiter umformen: $t={\frac {s_{0}}{v_{a}-v_{s}}}={\frac {s_{0}}{v_{a}-q\cdot v_{a}}}={\frac {s_{0}}{v_{a}\cdot (1-q)}}={\frac {q\cdot s_{0}}{v_{s}\cdot (1-q)}}$ ; für konstantes Verhältnis $q$ der beiden Geschwindigkeiten zeigen die letzten beiden Brüche die im Text behauptete umgekehrte Proprotionalität der Zeit $t$ zu $v_{a}$ bzw. $v_{s}$ . Die umgekehrte Proportionalität von $t$ zu $v_{s}$ bedeutet, dass Achilles die Schildkröte eher trifft, wenn jene schneller läuft. Das könnte zunächst verwundern; vorausgesetzt ist hier aber, dass in diesem Fall auch Achilles um den gleichen Faktor schneller läuft wie die Schildkröte (da $q$ als konstant vorausgesetzt wird).
Es ist – heute – möglich, auch mit Zenons Ansatz die Zeit $t$ auszurechnen, nach der Achilles die Schildkröte einholt. - Sei $s_{0}$ wie oben der Vorsprung der Schildkröte zu Beginn des Rennens, $t_{0}$ die Zeit, die Achilles benötigt, um $s_{0}$ zurückzulegen. Ferner sei die Schildkröte $q$ -mal langsamer als Achilles. Dann holt Achilles die Schildkröte nach der Zeit $t_{0}\cdot q$ ein weiteres Mal ein, nach der Zeit $(t_{0}\cdot q)\cdot q=t_{0}\cdot q^{2}$ ein drittes Mal usw. Mit $q^{0}=1$ ist die Summe aller von Zenon betrachteten Zeiten, die Achilles zurücklegt:
$t=t_{0}\cdot \sum _{n=0}^{\infty }q^{n}=t_{0}\cdot \lim _{n\to \infty }\sum _{k=0}^{n}q^{k}=t_{0}\cdot \lim _{n\to \infty }{\frac {1-q^{n+1}}{1-q}}={\frac {t_{0}}{1-q}}$ .
Es ist möglich, aber nicht zwingend erforderlich, $q$ wie oben als Quotienten ${\frac {v_{s}}{v_{a}}}$ zweier Geschwindigkeiten aufzufassen. Dann ist mit $t_{0}={\frac {s_{0}}{v_{a}}}$ weiter:
$t={\frac {t_{0}}{1-q}}={\frac {s_{0}}{v_{a}-q\cdot v_{a}}}={\frac {s_{0}}{v_{a}-v_{s}}};$
die konvergente geometrischen Reihe $t_{0}\cdot \sum _{n=0}^{\infty }q^{n}$ ergibt also das gleiche Ergebnis für $t$ wie die Rechnung in Anmerkung 1 ohne Zerlegung von $t$ nach Zenons Ansatz. Die Reihe erfüllt wegen $0<q<1$ ein Konvergenzkriterium, sodass Grenzwertrechnung ihr genau eine (exakte, als „Grenzwert“ bezeichnete) Zahl zuordnet, die sie im Unendlichen erreicht. Eine solche Mathematik war Zenon augenscheinlich nicht bekannt.
Sainsbury zeigt in Paradoxien die Unbestimmtheit des Problems anhand der Zweiteilung: Die Länge zwei wird halbiert, in zwei Längen eins, dann weiter eine Länge eins in zwei halbe, davon wieder eine halbe in zwei viertel und so weiter. Es ist offensichtlich, dass dabei die Zwei nicht überschritten wird, noch sich die Zeit dehnt. Es ist vielmehr der verbleibende Rest stets klar: Identisch mit dem letzten Teilungsglied (oben ein Viertel). (Es scheint somit kein Ziel Zenons zu sein, zu zeigen, dass das Rennen ewig währt noch unbestimmt lang ist. Als Argument bleibt, ähnlich wie beim Pfeilparadoxon, die Unmöglichkeit (in Einklang mit den fehlenden Aussagen der Mathematik über Unendlich bzw. ggf. Null) das Ziel zu erreichen.)
Mit Zenons Ansatz lässt sich auch der Weg $s$ ausrechnen, den Achilles im Zeitraum $t$ (von seinem Startpunkt bis zum Einholen der Schildkröte) zurücklegt. - In der Rechnung in Anmerkung 3 ist nur $t$ bzw. $t_{0}$ durch $s$ bzw. $s_{0}$ zu ersetzen:
$s=s_{0}\cdot \sum _{n=0}^{\infty }q^{n}={\frac {s_{0}}{1-q}}$ .
Werden Geschwindigkeiten eingeführt, so ist ohne Zerlegung in Teilwege unter Benutzung obiger Darstellung von $t$ :
$s=v_{a}\cdot t={\frac {v_{a}\cdot s_{0}}{v_{a}-v_{s}}}$ ;
Ausklammern von $v_{a}$ im Nenner und Kürzen liefert das gleiche Ergebnis wie die konvergente Reihe.

Literatur

Max Black: Achilles and the Tortoise. In: Analysis. Nr. 11, 1950, S. 91–101.
Simon Blackburn: Practical Tortoise Raising. In: Mind. Nr. 104, 1995, S. 696–711.
S. Brown: What the Tortoise taught us. In: Mind. Nr. 63, 1954, S. 170–179.
Florian Cajori: The Purpose of Zeno’s Arguments on Motion. In: Isis. Nr. 3/1, 1920, S. 7–20.
L. Carroll (C. L. Dogson): What the Tortoise said to Achilles. In: Mind. Nr. 104, 1995, S. 278–280.
M. Clark: Paradoxes, from A to Z. Routledge, London 2000.
Pascal Engel: Dummett, Achilles and the tortoise. In: L. Hahn, R. Auxier (Hrsg.): The philosophy of Michael Dummett (Library of Living philosophers). Open Court, La Salle, Ill. 2005.
Adolf Grünbaum: Modern Science and Zeno’s Paradoxes. Wesleyan University Press, Middletown 1967.
Andrew Harrison: Zeno’s Paper Chase. In: Mind. Nr. 76/304, 1967, S. 568–575.
J. M. Hinton, C. B. Martin: Achilles and the Tortoise. In: Analysis. Nr. 14/3, 1954, S. 56–68.
C. V. Jones: Zeno’s paradoxes and the first foundations of mathematics. (Spanish) In: Mathesis. Nr. 3/1, 1987.
S. Makin: Art. Zeno of Elea. In: Routledge Encyclopedia of Philosophy. Bd. 9, London 1998, S. 843–853.
R. Morris: Achilles in the Quantum Universe. Redwood Books, Trowbridge, Wiltshire 1997.
Jorge Luis Borges: Zwei Essays in Kabbala und Tango. S. Fischer Verlag, 1991.
Aloys Müller: Das Problem des Wettlaufs zwischen Achill und der Schildkröte. In: Archiv für Philosophie. Nr. 2, 1948, S. 106–111.
Stanislaus Quan: The Solution of Zeno’s First Paradox. In: Mind. Nr. 77/306, 1968, S. 206–221.
W. D. Ross: Aristotle’s Physics. Clarendon, Oxford 1936, xi–xii Bibliographie älterer Literatur zu den Paradoxien der Bewegung, S. 70–85 u. ö. Kommentar zu den Abschnitten bei Aristoteles.
Bertrand Russell: Our Knowledge of the External World. Kap. 5 und 6. Open Court, London/Chicago 1914.
Richard Mark Sainsbury: Paradoxien. (=Reclams Universal-Bibliothek 18135) Reclam, Stuttgart 2001, ISBN 3-15-018135-6.
Wesley C. Salmon (Hrsg.): Zeno’s paradoxes. Hacket, Indianapolis 1970, Nachdruck 2001, ISBN 0-87220-560-6.
Wesley C. Salmon: Space, Time and Motion. Kap. 2. Dickenson Publishing Co., Enrico, California and Belmont, California 1975.
T. Smiley: A Tale of Two Tortoises. In: Mind. Nr. 104, 1995, S. 725–736.
Roy Sorensen: A Brief History of the Paradox. Oxford University Press, 2003.
L. E. Thomas: Achilles and the Tortoise. In: Analysis. Nr. 12/4, 1952, S. 92–94.
J. F. Thomson: What Achilles should have said to the Tortoise. In: Ratio. Nr. 3, 1960, S. 95–105.

Weblinks

Wikiquote: Arnfrid Astel – Zitate

Christoph Bock: Elemente der Analysis (PDF; 2,2 MB) S. 59 f.
Nick Huggett: Zeno’s Paradoxes. In: Edward N. Zalta (Hrsg.): Stanford Encyclopedia of Philosophy.
Eintrag in Wolfram’s Math World (Englisch, mit weiterer Literatur)
Peter Lynds: Zeno’s Paradoxes: A Timely Solution. (Englisch mit weiterer Literatur; PDF-Datei; 166 kB)
Artikel in: Matroids Matheplanet.
Ulrich Eckhardt: Zenon (PDF; 320 kB)
Zenon und die Zeitlupe. In: Wolfram Heinrich: Zenon, Achilles und die Schildkröte. Der vergessene Denker Costabile Matarazzo. http://derfranzehatgsagt.blogspot.com/2011/08/zenon-achilles-und-die-schildkrote.html

Einzelnachweise

Nach Peter Janich: Achilles und die Schildkröte. in: Jürgen Mittelstraß (Hrsg.): Enzyklopädie Philosophie und Wissenschaftstheorie. Band 1. Metzler, Stuttgart 1995, Nachdruck 2004, S. 41, ISBN 3-476-02012-6.
Aristoteles, Physik VI,9,239b14–240a18 in der Formulierung, dass „auch das langsamste Tier im Laufe nicht eingeholt werden könne vom schnellsten, da der Verfolger immer erst dahin kommen müsse, von wo das fliehende Tier fortgelaufen ist, so daß das langsamere immer einen Vorsprung behalte“.
Aristoteles: Physik. Abgerufen am 16. Oktober 2013 (Altgriechischer Originaltext, siehe im Bildschirmausschnitt §4).
Simplicius, On Aristotle’s Physics 1014,10, vgl.: S. M. Chohen, P. Curd, C. D. C. Reeve (Hrsg.): Readings in Ancient Greek Philosophy From Thales to Aristotle. Hackett, Indianapolis/Cambridge 1995, S. 58 f.
Mind. Nr. 1, 1895, S. 278–280.
Hierzu siehe zum Beispiel Pascal Engel: Dummett: Achilles and the tortoise.. In: L. Hahn, R. Auxier (Hrsg.): The philosophy of Michael Dummett (Library of Living philosophers). Open Court, La Salle, Ill. 2005.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[anm1-1] Sei $t$ die Zeit, die vom Beginn des Rennens bis zu dem Zeitpunkt verstreicht, zu dem Achilles die Schildkröte einholt, $s$ der Weg, den Achilles während der Zeit $t$ zurücklegt, $s'$ der Weg, den die Schildkröte während der Zeit $t$ zurücklegt, $s_{0}$ der Vorsprung der Schildkröte zu Beginn des Rennens, $v_{a}$ die Geschwindigkeit Achilles’, $v_{s}$ die Geschwindigkeit der Schildkröte. Dann lässt sich t wie folgt berechnen:
$v_{a}\cdot t=s=s_{0}+s'=s_{0}+v_{s}\cdot t$ , also $s_{0}=v_{a}\cdot t-v_{s}\cdot t=(v_{a}-v_{s})\cdot t$ ; mit $v_{a}-v_{s}\neq 0$ folgt nach Division: $t={\frac {s_{0}}{v_{a}-v_{s}}}$ .
Letzteres zeigt die im Text behauptete Proportionalität der Zeit $t$ zum Vorsprung $s_{0}$ der Schildkröte und die umgekehrte Proportionalität von $t$ zur Geschwindigkeitsdifferenz $v_{a}-v_{s}$ .

[anm2-2] (Mit $v_{a}\neq 0$ ) sei weiter $q={\frac {v_{s}}{v_{a}}}$ das Verhältnis der Geschwindigkeiten, sodass $v_{s}=q\cdot v_{a}$ , (mit $v_{s}\neq 0$ ) auch ${\frac {1}{v_{a}}}={\frac {q}{v_{s}}}$ . Wegen $v_{a}-v_{s}\neq 0$ ist $q\neq 1$ , und der Ausdruck für $t$ lässt sich weiter umformen: $t={\frac {s_{0}}{v_{a}-v_{s}}}={\frac {s_{0}}{v_{a}-q\cdot v_{a}}}={\frac {s_{0}}{v_{a}\cdot (1-q)}}={\frac {q\cdot s_{0}}{v_{s}\cdot (1-q)}}$ ; für konstantes Verhältnis $q$ der beiden Geschwindigkeiten zeigen die letzten beiden Brüche die im Text behauptete umgekehrte Proprotionalität der Zeit $t$ zu $v_{a}$ bzw. $v_{s}$ . Die umgekehrte Proportionalität von $t$ zu $v_{s}$ bedeutet, dass Achilles die Schildkröte eher trifft, wenn jene schneller läuft. Das könnte zunächst verwundern; vorausgesetzt ist hier aber, dass in diesem Fall auch Achilles um den gleichen Faktor schneller läuft wie die Schildkröte (da $q$ als konstant vorausgesetzt wird).

[anm3-4] Es ist – heute – möglich, auch mit Zenons Ansatz die Zeit $t$ auszurechnen, nach der Achilles die Schildkröte einholt. - Sei $s_{0}$ wie oben der Vorsprung der Schildkröte zu Beginn des Rennens, $t_{0}$ die Zeit, die Achilles benötigt, um $s_{0}$ zurückzulegen. Ferner sei die Schildkröte $q$ -mal langsamer als Achilles. Dann holt Achilles die Schildkröte nach der Zeit $t_{0}\cdot q$ ein weiteres Mal ein, nach der Zeit $(t_{0}\cdot q)\cdot q=t_{0}\cdot q^{2}$ ein drittes Mal usw. Mit $q^{0}=1$ ist die Summe aller von Zenon betrachteten Zeiten, die Achilles zurücklegt:
$t=t_{0}\cdot \sum _{n=0}^{\infty }q^{n}=t_{0}\cdot \lim _{n\to \infty }\sum _{k=0}^{n}q^{k}=t_{0}\cdot \lim _{n\to \infty }{\frac {1-q^{n+1}}{1-q}}={\frac {t_{0}}{1-q}}$ .
Es ist möglich, aber nicht zwingend erforderlich, $q$ wie oben als Quotienten ${\frac {v_{s}}{v_{a}}}$ zweier Geschwindigkeiten aufzufassen. Dann ist mit $t_{0}={\frac {s_{0}}{v_{a}}}$ weiter:
$t={\frac {t_{0}}{1-q}}={\frac {s_{0}}{v_{a}-q\cdot v_{a}}}={\frac {s_{0}}{v_{a}-v_{s}}};$
die konvergente geometrischen Reihe $t_{0}\cdot \sum _{n=0}^{\infty }q^{n}$ ergibt also das gleiche Ergebnis für $t$ wie die Rechnung in Anmerkung 1 ohne Zerlegung von $t$ nach Zenons Ansatz. Die Reihe erfüllt wegen $0<q<1$ ein Konvergenzkriterium, sodass Grenzwertrechnung ihr genau eine (exakte, als „Grenzwert“ bezeichnete) Zahl zuordnet, die sie im Unendlichen erreicht. Eine solche Mathematik war Zenon augenscheinlich nicht bekannt.

[anm3.2-5] Sainsbury zeigt in Paradoxien die Unbestimmtheit des Problems anhand der Zweiteilung: Die Länge zwei wird halbiert, in zwei Längen eins, dann weiter eine Länge eins in zwei halbe, davon wieder eine halbe in zwei viertel und so weiter. Es ist offensichtlich, dass dabei die Zwei nicht überschritten wird, noch sich die Zeit dehnt. Es ist vielmehr der verbleibende Rest stets klar: Identisch mit dem letzten Teilungsglied (oben ein Viertel). (Es scheint somit kein Ziel Zenons zu sein, zu zeigen, dass das Rennen ewig währt noch unbestimmt lang ist. Als Argument bleibt, ähnlich wie beim Pfeilparadoxon, die Unmöglichkeit (in Einklang mit den fehlenden Aussagen der Mathematik über Unendlich bzw. ggf. Null) das Ziel zu erreichen.)

[anm4-6] Mit Zenons Ansatz lässt sich auch der Weg $s$ ausrechnen, den Achilles im Zeitraum $t$ (von seinem Startpunkt bis zum Einholen der Schildkröte) zurücklegt. - In der Rechnung in Anmerkung 3 ist nur $t$ bzw. $t_{0}$ durch $s$ bzw. $s_{0}$ zu ersetzen:
$s=s_{0}\cdot \sum _{n=0}^{\infty }q^{n}={\frac {s_{0}}{1-q}}$ .
Werden Geschwindigkeiten eingeführt, so ist ohne Zerlegung in Teilwege unter Benutzung obiger Darstellung von $t$ :
$s=v_{a}\cdot t={\frac {v_{a}\cdot s_{0}}{v_{a}-v_{s}}}$ ;
Ausklammern von $v_{a}$ im Nenner und Kürzen liefert das gleiche Ergebnis wie die konvergente Reihe.

[3] Nach Peter Janich: Achilles und die Schildkröte. in: Jürgen Mittelstraß (Hrsg.): Enzyklopädie Philosophie und Wissenschaftstheorie. Band 1. Metzler, Stuttgart 1995, Nachdruck 2004, S. 41, ISBN 3-476-02012-6.

[7] Aristoteles, Physik VI,9,239b14–240a18 in der Formulierung, dass „auch das langsamste Tier im Laufe nicht eingeholt werden könne vom schnellsten, da der Verfolger immer erst dahin kommen müsse, von wo das fliehende Tier fortgelaufen ist, so daß das langsamere immer einen Vorsprung behalte“.

[8] Aristoteles: Physik. Abgerufen am 16. Oktober 2013 (Altgriechischer Originaltext, siehe im Bildschirmausschnitt §4).

[9] Simplicius, On Aristotle’s Physics 1014,10, vgl.: S. M. Chohen, P. Curd, C. D. C. Reeve (Hrsg.): Readings in Ancient Greek Philosophy From Thales to Aristotle. Hackett, Indianapolis/Cambridge 1995, S. 58 f.

[10] Mind. Nr. 1, 1895, S. 278–280.

[11] Hierzu siehe zum Beispiel Pascal Engel: Dummett: Achilles and the tortoise.. In: L. Hahn, R. Auxier (Hrsg.): The philosophy of Michael Dummett (Library of Living philosophers). Open Court, La Salle, Ill. 2005.