Sterngebiet

In der Mathematik versteht man unter einer sternförmigen Menge eine Teilmenge ${\displaystyle M}$ des ${\displaystyle \mathbb {R} ^{n}}$, zu der es einen Punkt ${\displaystyle x_{0}}$ gibt (ein Sternzentrum bzw. einen Sternmittelpunkt), von dem aus alle Punkte der Menge „sichtbar“ sind, das heißt, jede gerade Verbindungsstrecke von ${\displaystyle x_{0}}$ zu einem beliebigen Punkt ${\displaystyle x\in M}$ liegt vollständig in ${\displaystyle M}$.

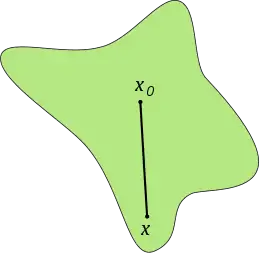
sternförmige Menge mit Sternzentrum ${\displaystyle x_{0},}$ ihr Inneres (grün) ist ein Sterngebiet

Ist e​ine sternförmige Menge zusätzlich offen, s​o spricht m​an von e​inem Sterngebiet.

Formale Definition

Eine Menge ${\displaystyle M\subseteq \mathbb {R} ^{n}}$ heißt sternförmig, wenn es ein ${\displaystyle x_{0}\in M}$ gibt, so dass für alle ${\displaystyle x\in M}$ die Strecke

${\displaystyle [x_{0}\,x]=\left\{x_{0}+t(x-x_{0})\;\colon \;t\in [0,1]\right\}}$

eine Teilmenge von ${\displaystyle M}$ ist.

Bemerkungen

• Jede nichtleere konvexe Menge ist sternförmig.
• Die Menge der möglichen Sternzentren heißt auch Zentrum der Menge. Man kann zeigen, dass es stets konvex ist. Eine Menge stimmt genau dann mit ihrem Zentrum überein, wenn sie konvex ist.
• Sternförmige Mengen sind kontrahierbar. Daraus folgt:
• Sternförmige Mengen sind einfach zusammenhängend, also insbesondere wegzusammenhängend.
• Ein Sterngebiet ist ein Gebiet.

Siehe auch

• Problem der Museumswächter

Literatur

• Konrad Königsberger: Analysis 2. 1. Auflage. Springer, 1993, ISBN 3-540-54723-1, S. 345

Weblinks

• sternförmiges Gebiet in Kurvenintegrale und konservative Vektorfelder auf Mathematik Online (Uni Stuttgart)
• Eric W. Weisstein: star convex. In: MathWorld (englisch).
• star shaped auf PlanetMath (englisch)