Transformator

Ein Transformator (von lateinisch transformare ‚umformen, umwandeln‘; auch Umspanner, kurz Trafo) ist ein Bauelement der Elektrotechnik. Er besteht meist aus zwei oder mehr Spulen (Wicklungen), die in der Regel aus isoliertem Kupferdraht gewickelt sind und sich auf einem gemeinsamen Magnetkern befinden. Ein Transformator wandelt eine Eingangswechselspannung, die an einer der Spulen angelegt ist, in eine Ausgangswechselspannung um, die an der anderen Spule abgegriffen werden kann. Dabei entspricht das Verhältnis von Eingangs- und Ausgangsspannung dem Verhältnis der Windungsanzahlen der beiden Spulen. So wird zum Beispiel bei einem Windungsverhältnis von 20 zu 1 eine Eingangsspannung von 240 Volt in eine Ausgangsspannung von 12 Volt transformiert. Je nach Auslegung des Transformators kann die Ausgangsspannung somit kleiner, größer oder gleich der Eingangsspannung sein.

Aus Komponenten zusammensetzbarer Transformator zu Anschauungszwecken. Oben der U-förmige Teil des Eisenkerns, im mittleren Bild mit aufgesteckten Spulen; im unteren Bild mit einem weiteren ferromagnetischen (Eisen-)Joch über dem „U“-Kern, mit dem der magnetische Kreis durchgehend geschlossen wird.

Transformatoren dienen vielfach zur Spannungswandlung in Energieversorgungsanlagen und in technischen Geräten, dabei insbesondere in Netzteilen zur Bereitstellung von Kleinspannungen in vielen Arten von elektrischen und elektronischen Geräten. Weiterhin werden sie bei der Signalübertragung und der Schutztrennung benötigt.

Geschichte

1885: Transformator von Zipernowsky, Déri und Bláthy

Patentzeichnung von William Stanley 1886

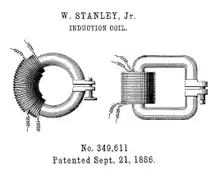
Obwohl das Induktionsprinzip seit den Entdeckungen Michael Faradays von 1831 bekannt war, wurde der Transformator erst 44 Jahre später entwickelt. Pawel Nikolajewitsch Jablotschkow entwickelte 1875 eine verbesserte Form der Kohlebogenlampe und verwendete für deren Betrieb Induktionsspulen, die prinzipiell einen Transformator darstellten.[1] Er beschäftigte sich jedoch nicht weiter mit diesen Geräten. Lucien Gaulard und John Dixon Gibbs stellten 1881 einen Transformator in London aus und 1882 wurde ihnen dafür das englische Patent Nr. 4362 zuerkannt.[2] Der Begriff Transformator war zur damaligen Zeit noch nicht üblich; die Geräte wurden als Sekundär-Generator bezeichnet. Davon leitet sich die bis heute übliche Zuordnung der Transformatoren zum Bereich der elektrischen Maschinen ab.[3] Károly Zipernowsky, Miksa Déri und Ottó Titusz Bláthy (alle drei Ungarn) erhielten 1885 ein Patent auf den Transformator. Dieser war mechanisch nach dem umgekehrten Prinzip der heutigen Transformatoren aufgebaut; die Leiterspulen waren um einen festen Kern aus unmagnetischem Material gewunden, darüber wurden dicke Eisendraht-Lagen gelegt, die eine ferromagnetische Schale bildeten. Dieser Transformator wurde vom Unternehmen Ganz & Cie aus Budapest weltweit vertrieben.

Wesentlichen Anteil an der Verbreitung des Wechselstromsystems und mit ihm des Transformators hatte der Amerikaner George Westinghouse. Er erkannte die Nachteile der damals von Thomas A. Edison betriebenen und favorisierten Energieverteilung mittels Gleichstrom und setzte stattdessen auf Wechselstrom (vgl. Stromkrieg). 1885 erwarb Westinghouse die Patentrechte von Gaulard und Gibbs[2] und importierte eine Anzahl von deren Sekundär-Generatoren sowie einen Generator von Siemens. Damit baute er in Pittsburgh ein Stromnetz mit Wechselspannung für die elektrische Beleuchtung. William Stanley führte im gleichen Jahr als Chefingenieur von Westinghouse in Pittsburgh wesentliche Verbesserungen an Lucien Gaulards und John Gibbs’ Gerät durch. Westinghouse installierte 1886 in Great Barrington, Massachusetts, einen Wechselspannungsgenerator, dessen 500 V Wechselspannung zur Verteilung auf 3.000 V hochtransformiert und zum Betrieb der elektrischen Beleuchtung an den Anschlussstellen wieder auf 100 V heruntertransformiert wurde. Der wachsende Einsatz von Transformatoren führte in Verbindung mit der Schaffung von Wechselstromnetzen zum weltweiten Fortschreiten der Elektrifizierung.

Michail Dolivo-Dobrowolski entwickelte Anfang der 1890er-Jahre bei der AEG in Berlin den ersten Transformator für dreiphasigen Wechselstrom und führte den Begriff Drehstrom ein.[4][5][6] Sein Drehstromtransformator wurde 1891, auf Anregung von Oskar von Miller, für die erste Fernübertragung elektrischer Energie mit Dreiphasenwechselstrom eingesetzt. Die Leitung ging am 24. August 1891 zwischen Lauffen am Neckar und der Internationalen Elektrotechnischen Ausstellung im 175 km entfernten Frankfurt am Main in Betrieb. Die in einem Wasserkraftwerk erzeugte Spannung von 50 V wurde zur Übertragung auf 15 kV hochtransformiert.

Bereits 1888 veröffentlichte der Münchner Elektroingenieur Friedrich Uppenborn ein Buch zur Geschichte des Transformators.[7] Gisbert Kapp erarbeitete bis 1907 die Grundlagen für die Berechnung und den Bau von Transformatoren.[8]

Grundprinzip

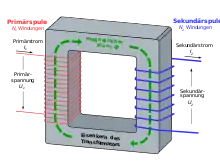
Prinzipskizze eines Transformators

Idealtypisch besteht ein Transformator aus einem magnetischen Kreis, welcher als Transformatorkern bezeichnet wird und mindestens zwei stromdurchflossene Wicklungen hat. Die der elektrischen Energiequelle zugewandte Wicklung wird als Primärseite bezeichnet. Diejenige, an welcher sich die elektrische Last befindet, wird als Sekundärseite bezeichnet.

Die Wirkungsweise lässt sich durch die folgenden Mechanismen beschreiben:[9]

Eine Wechselspannung auf der Primärseite des Transformators bewirkt entsprechend dem Induktionsgesetz einen wechselnden magnetischen Fluss im Kern. Der wechselnde magnetische Fluss wiederum induziert auf der Sekundärseite des Transformators eine Spannung (Spannungstransformation).
Ein Wechselstrom in der Sekundärwicklung bewirkt dem Ampèreschen Gesetz entsprechend einen Wechselstrom in der Primärwicklung (Stromtransformation).

Bei niedriger Wechselstromfrequenz wird typischerweise ein Eisenkern aus einem ferromagnetischen Material hoher Permeabilität verwendet. Damit können gegenüber Transformatoren ohne Eisenkern hohe magnetische Wechselflussdichten und damit eine wesentlich höhere Windungsspannung erzielt werden, was gewährleistet, dass die übertragbare Leistung groß ist im Vergleich zur Verlustleistung, die durch den ohmschen Widerstand in den Wicklungen entsteht. Einfach ausgedrückt, benötigt ein Transformator mit Eisenkern wesentlich weniger Windungen auf den Wicklungen als ein Trafo ohne Eisenkern.

Zum magnetischen Fluss im Unterpunkt 1 gehört ein Magnetfeld, welches ähnlich wie in einem Elektromagneten einen Stromfluss in der Primärspule bedingt. Der zum Aufbau des magnetischen Feldes benötigte Strom heißt Magnetisierungsstrom. Der Primärstrom, der entsprechend Unterpunkt 2 von der Stromtransformation herrührt, heißt primärer Zusatzstrom. Er fließt zusätzlich zum Magnetisierungsstrom und ist in der Regel als Wirkstrom wesentlich größer als dieser.

Funktionsweise

Idealer Transformator

Unter einem idealen Transformator versteht man einen in der Praxis nicht realisierbaren, verlustfreien Transformator. Dabei werden die Widerstände R₁ und R₂ der Primär- beziehungsweise Sekundärwicklung mit R₁ = R₂ = 0 Ω angenommen. Ebenso wird angenommen, dass keine Streuung des magnetischen Flusses $\Phi$ stattfindet. Diese Modellvorstellung ist hilfreich bei der Funktionsbeschreibung. In der Praxis treten mehr oder weniger große Abweichungen auf, die Gesetzmäßigkeiten gelten nur näherungsweise.

3D-Zeichnung eines typischen Netztransformators. Die innere Wicklung ist für Netzspannung (die Speisespannung) ausgelegt – erkennbar an der großen Windungszahl aus dünnem Draht. An der äußeren Wicklung wird die Ausgangsspannung entnommen. Sie ist meist wesentlich geringer und erfordert daher eine kleinere Windungszahl – der Strom ist jedoch höher, daher ist die Drahtdicke größer. Der Trafokern besteht aus dünnen Eisenblechen, die, um Wirbelströme zu vermeiden, gegeneinander isoliert sind.

Beim idealen Transformator sind die Spannungen an den Wicklungen aufgrund der elektromagnetischen Induktion proportional zur Änderungsgeschwindigkeit des magnetischen Flusses und zur Windungszahl der Wicklung. Daraus folgt, dass sich die Spannungen so zueinander verhalten wie die Windungszahlen. Sind N₁, N₂, U₁ und U₂ die Windungszahlen beziehungsweise die Effektivwerte der primär- und sekundärseitigen Spannungen, so gilt beim idealen Transformator

{\frac {U_{2}}{U_{1}}}={\frac {N_{2}}{N_{1}}}

bzw.

U_{2}={\frac {N_{2}}{N_{1}}}\cdot U_{1}

Das Verhältnis von Windungszahlen, beziehungsweise der primär- und sekundärseitigen Spannungen, wird auch als Übersetzungsverhältnis ü bezeichnet:

{\ddot {u}}={\frac {U_{1}}{U_{2}}}={\frac {N_{1}}{N_{2}}}

bzw.

U_{2}={\frac {U_{1}}{\ddot {u}}}

Durch geeignete Wahl des Übersetzungsverhältnisses ü, also der Windungszahlen N₁ und N₂, können mit einem Transformator Wechselspannungen sowohl hochtransformiert werden, indem ü kleiner 1 gewählt wird, oder heruntertransformiert, wenn ü größer 1 gewählt ist.

Aus der Annahme eines idealen Transformators ergibt sich, dass die Verlustleistung eines idealen Transformators Null ist. Er hat einen Wirkungsgrad von η = 100%. Damit muss die einem idealen Transformator zugeführte Leistung P₁ gleich der abgegebenen Leistung P₂ sein:

P_{1}=P_{2}

bzw.

U_{1}\cdot I_{1}=U_{2}\cdot I_{2}

Daraus wiederum kann man das Stromübersetzungsverhältnis des idealen Transformators bestimmen. Die Ströme verhalten sich umgekehrt proportional zum Übersetzungsverhältnisses:

{\frac {I_{1}}{I_{2}}}={\frac {1}{\ddot {u}}}

Da man nun die Strom- und Spannungsverhältnisse am idealen Transformator kennt kann man weiterhin das Übersetzungsverhältnis von Wechselstromimpedanzen durch den idealen Transformator bestimmen:

{\frac {Z_{1}}{Z_{2}}}={\frac {U_{1}}{I_{1}}}\cdot {\frac {I_{2}}{U_{2}}}={\ddot {u}}^{2}

Das heißt, ein idealer Transformator transformiert eine Wechselstromimpedanz quadratisch mit dem Übersetzungsverhältnis.

Wird an die sekundäre Wicklung ein Verbraucher angeschlossen, so entnimmt dieser der Sekundärspule elektrische Energie. Dabei kommt ein Strom auf der Sekundärseite zustande und der Primärstrom vergrößert sich. Im Gegensatz zu den Spannungen an den Wicklungen sind die Ströme in den Wicklungen jedoch entgegengesetzt gerichtet: Wenn der Primärstrom bezogen auf den Kern rechtsherum durch die Spule fließt, fließt der Sekundärstrom linksherum und umgekehrt (Lenzsche Regel). Physikalisch lässt sich der gegensinnige Stromfluss mit dem Durchflutungssatz erklären. Dabei wird davon ausgegangen, dass die von der Primärspannung U₁ erzeugte Flussdichte B im Kern nur endlich große Werte annimmt und dass die Permeabilitätszahl μ_r des Kerns sehr groß ist. Unter diesen Umständen wird die magnetische Feldstärke H im Kern so klein, dass sie nahezu vernachlässigbar ist (H → 0), und die Anwendung des Durchflutungssatzes auf einen Integrationsweg entlang des Kernes ergibt:

I_{2}={\frac {N_{1}}{N_{2}}}\cdot I_{1}

.

Die gegensinnige Flussrichtung des Stromes wird im Schaltbild durch den aus dem Transformator herausgerichteten Strompfeil I₂ gekennzeichnet.

Realer Transformator

Ideale Transformatoren sind praktisch nicht realisierbar. Ein realer Transformator unterscheidet sich u. a. folgendermaßen vom idealen Transformator:

Die Wicklungen haben Widerstände und parasitäre Kapazitäten;
im Eisenkern treten Wirbelstrom- und Ummagnetisierungs-Verluste auf
nicht der gesamte magnetische Fluss, den die Primärwicklung erzeugt, führt auch durch die Sekundärwicklung; es tritt ein Streufluss auf. Daher entspricht das Spannungsverhältnis der Wicklungen auch im Leerlauf nicht deren Windungszahlenverhältnis.
Der Kern verträgt nur eine begrenzte Flussdichte bis zur Sättigungsmagnetisierung. Bis dahin ist das Verhältnis zwischen Flussdichte und Feldstärke (Permeabilität) nicht linear. Daher weicht der Verlauf des Magnetsisierungsstromes mehr oder weniger stark von der Sinusform ab.
der Kern ändert aufgrund der Magnetostriktion in geringem Maß seine Form, wenn sich das Magnetfeld ändert, wodurch eventuell Schall abgestrahlt werden kann.

Die Widerstände der Wicklungen, die Ummagnetisierung und die Wirbelströme führen zu Energieverlusten. Die Verluste aufgrund der Widerstände der Wicklungen heißen Kupferverluste, die Verluste durch die Ummagnetisierung heißen Hystereseverluste, und die Verluste aufgrund von Wirbelströmen heißen Wirbelstromverluste. Hystereseverluste und Wirbelstromverluste werden unter dem Begriff Eisenverluste zusammengefasst.

Die Kupferverluste hängen quadratisch von der Belastung des Transformators ab, d. h., sie sind proportional zum Quadrat der Ströme in jeder Wicklung I_x. Die Eisenverluste sind fast unabhängig von der Belastung, aber in etwa proportional zum Quadrat der magnetischen Flussdichte im Kern. Die Hystereseverluste sind außerdem proportional zur Frequenz, die Wirbelstromverluste sind proportional zum Quadrat der Frequenz.[10]

Streuflüsse bewirken, dass die Sekundärspannung etwas geringer ist als beim idealen Transformator.

Die Sättigungsmagnetisierung begrenzt die mögliche Betriebsfrequenz nach unten beziehungsweise bei gegebener Frequenz und Windungszahl die mögliche Primärspannung nach oben. Wird die Grenze überschritten und die Sättigung erreicht, fließen primärseitig sehr hohe Ströme, während sekundärseitig die Spannung sehr gering wird. Durch Erhöhung der Primärwindungszahl lässt sie sich jedoch auf Kosten des Wickelraumes und der Zunahme der Kupferverluste im Praxisfall gegebenenfalls verhindern. Die Sekundärwindungszahlen erhöhen sich dann natürlich entsprechend ebenfalls. Die Sättigungsmagnetisierung spielt auch beim Einschalten des Transformators eine wichtige Rolle; der Einschaltstrom kann dabei kurzzeitig ein Vielfaches des Nennstroms betragen.

Belasteter und unbelasteter Transformator

Wenn an der Sekundärwicklung kein Verbraucher angeschlossen ist, liegt Leerlauf vor. Der Transformator ist unbelastet. Ein verlustloser Transformator im Leerlauf verhält sich wie eine ideale Spule. Wird primärseitig eine sinusförmige Wechselspannung angeschlossen, fließt ein um 90 Grad phasenverschobener Strom, der als Magnetisierungsstrom bezeichnet wird und dem Aufbau des magnetischen Feldes dient. Beim realen Transformator ist die Phasenverschiebung des Leerlaufstroms gegenüber der Primärspannung aufgrund der Eisenverluste kleiner als 90 Grad.[11][12] Im Leerlauf sind die Eisenverluste aufgrund des nur geringen Eingangsstroms viel größer als die Kupferverluste durch den Leerlaufstrom in der Primärspule.

Wegen des in der Realität meist nichtlinearen Zusammenhangs zwischen magnetischer Feldstärke $H$ und magnetischer Induktion $B$ im Kern ist der Magnetisierungsstrom, anders als beim verlustlosen Transformator, nicht sinusförmig.[12]

Wenn der Transformator sekundärseitig belastet wird, fließt ein Sekundärstrom. Dieser ändert den Fluss im Kern und damit die in der Primärwicklung induzierte Gegenspannung. Um das Spannungsgleichgewicht auf der Primärseite aufrechtzuerhalten, muss diese Flussänderung durch einen primärseitigen Zusatzstrom zusätzlich zum Magnetisierungsstrom kompensiert werden. Es muss sich ein Gleichgewicht zwischen der vom Sekundärstrom erzeugten Durchflutung und der durch den primärseitigen Zusatzstrom bedingten Durchflutung einstellen. Bei Nennlast ist der Primärstrom deswegen viel größer als im Leerlauffall.[11] Bei Belastung sinkt die magnetische Flussdichte geringfügig ab.

Wird die Sekundärseite kurzgeschlossen und der Eingangsstrom auf den Strom bei Nennlast geregelt, muss dazu die Primärspannung reduziert werden. Die so eingestellte Primärspannung wird als Kurzschlussspannung bezeichnet, welche nicht absolut, sondern als prozentuales Verhältnis zur Nennspannung angegeben wird. Bei Leistungstransformatoren beträgt sie zwischen 5 % und 20 %,[13] bei Kleintransformatoren liegt sie zwischen 15 % und 40 %, bei Schweißtransformatoren beträgt sie 100 %.

Transformatoren mit hoher Kurzschlussspannung heißen spannungsweich, solche mit niedriger Kurzschlussspannung heißen spannungssteif. Die Kurzschlussspannung hängt wesentlich von der Konstruktion des Kerns und der Lage der Spulen zueinander ab: hohe Streuflüsse führen zu hohen Kurzschlussspannungen.[14] Siehe auch Streufeldtransformator.

Als Kurzschlussstrom wird jener Strom bezeichnet, der bei sekundärseitigem Kurzschluss und Nennspannung fließt. Er ist viel höher als der Nennstrom und kann den Transformator in kurzer Zeit zerstören. Der Kurzschlussstrom ist umso höher, je niedriger die Kurzschlussspannung ist. Für Transformatoren mit niedriger Kurzschlussspannung sind Kurzschlüsse daher gefährlich. Transformatoren, die so ausgelegt sind, dass sie im Kurzschlussfall nicht zerstört werden, werden als kurzschlussfest bezeichnet. In der Regel werden nur Kleintransformatoren bis zu wenigen VA Leistung, wie zum Beispiel Klingeltrafos, kurzschlussfest ausgelegt. Aber auch große Leistungstrafos müssen zumindest einen kurzfristigen Stoßkurzschlussstrom ohne mechanische Beschädigung durch die auftretenden Lorentzkräfte überstehen können.[15]

Wirkungsgrad

Typischer Wirkungsgradverlauf eines Transformators über die Belastung am Beispiel eines 100-VA-Netztransformators

Der Wirkungsgrad eines Transformators ist das Verhältnis der elektrischen Leistung, die den Transformator sekundärseitig verlässt, zur Leistung, die primärseitig in ihn hineinfließt. Wegen der Eisen- und Kupferverluste ist er kleiner als 1. Transformatoren hoher Nennleistung haben Wirkungsgrade von mehr als 99 %, während der Wirkungsgrad von Kleintransformatoren (z. B. 100 VA) um 80 % liegt, und Kleinsttransformatoren (1 VA) kaum auf 50 % Wirkungsgrad kommen. Bei höherer Frequenz, z. B. in Schaltnetzteilen, können auch kleine Transformatoren einen hohen Wirkungsgrad erreichen.

Kurzzeitig können Transformatoren stark überlastet werden. Vom Kurzzeit-Betrieb wird zum Beispiel bei Lötpistolen, aber auch bei Elektrolokomotiven Gebrauch gemacht. Transformatoren liefern ein Maximum an Ausgangsleistung bei einem Wirkungsgrad von 50 % (Leistungsanpassung). Im nebenstehenden Diagramm ist dieser Punkt ganz rechts am Kurvenende – der dem Beispiel zugrunde liegende Transformator liefert dort etwa das 2,5fache seiner Nennleistung.

Maschinentransformatoren sind dauernd belastet, sie werden auf maximalen Wirkungsgrad dimensioniert, d. h., dass bei Nennlast Eisen- und Kupferverluste etwa gleich hoch sind.[16]

Bei einem Ortsnetztransformator, der im Stromnetz verwendet wird, liegt die mittlere Belastungsdauer nur bei ungefähr 40 % der Einschaltdauer, daher können hier höhere Kupferverluste in Kauf genommen werden, während die Eisenverluste stärker reduziert werden. Solche Transformatoren werden auf ihren Jahreswirkungsgrad optimiert. Damit wird das Verhältnis der insgesamt pro Jahr primär- und sekundärseitig umgesetzten Energiemengen bezeichnet. Der Jahreswirkungsgrad liegt umso höher, je größer das Verhältnis zwischen Belastungs- und Einschaltdauer ist.

Netzwerkmodellierung

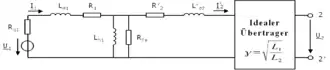
Ersatzschaltbild eines realen Transformators

Die Netzwerkmodellierung eines Transformators verfolgt das Ziel, die wesentlichen nichtidealen Eigenschaften eines Transformators mit einer geringen Zahl an Parametern zu beschreiben. Das nebenstehende Ersatzschaltbild zeigt eine häufig vorgenommene Modellierung mithilfe von linearen Bauelementen.[17] Dabei haben die einzelnen Bauelemente die folgende Bedeutung:

$U_{\mathrm {p} }$ : primärseitige Spannungsquelle
$U_{\mathrm {s} }=U_{2}$ : Ausgangsspannung
$I_{1}$ , $I_{2}'$ : Eingangsstrom und transformierter Ausgangsstrom
$R_{\mathrm {q1} }$ : Innenwiderstand der primärseitigen Spannungsquelle
$L_{\mathrm {\sigma 1} }$ , $L'_{\mathrm {\sigma 2} }$ : Streuinduktivität der Primärseite und transformierte Streuinduktivität der Sekundärseite
$R_{1}$ , $R'_{2}$ : Wicklungswiderstand der Primärseite und transformierter Wicklungswiderstand der Sekundärseite
$L_{\mathrm {h1} }$ : Hauptinduktivität, die den Magnetisierungsstrom führt
$R_{\mathrm {Fe} }$ : lineare Modellierung der meist nichtlinearen Eisenverluste im Kern (Fe: Eisen)

Auf die Modellierung der parasitären Kapazitäten der Wicklungen wurde im abgebildeten Modell verzichtet. Ebenso werden nichtlineare Eigenschaften des Transformators nicht abgebildet.

Der eingezeichnete ideale Transformator gehorcht den Transformationsgleichungen:

{\frac {{\underline {U}}_{1}}{{\underline {U}}_{2}}}=\gamma {\text{ und }}{\frac {{\underline {I}}_{1}}{{\underline {I}}_{2}}}={\frac {1}{\gamma }}.

Der Übertragungsfaktor $\gamma =N_{1}/N_{2}$ bezeichnet dabei das Verhältnis der Windungszahlen von Primär- und Sekundärseite.

Die Größen, die mit einem zusätzlichen Strich ' gekennzeichnet sind, wurden von der Sekundärseite zur Primärseite transformiert. Bei der Transformation einer Impedanz ${\underline {Z}}$ von der Sekundärseite zu einer Impedanz $Z'$ auf der Primärseite gilt die folgende Transformationsgleichung:

{\underline {Z'}}=\gamma ^{2}{\underline {Z}}

Die Impedanztransformation bedeutet, dass die Eingangsklemmen eines Transformators für einen elektrischen Schaltkreis wie ein Widerstand $\gamma ^{2}\cdot R$ wirken, wenn an die Sekundärseite ein Widerstand R angeschlossen wird. Somit können mithilfe eines Transformators Widerstände vergrößert oder verkleinert werden, indem das Windungsverhältnis $\gamma$ geändert wird.

Die Impedanztransformation wird in elektronischen Schaltungen häufig zur Anpassung eines Netzwerkes an den Wellenwiderstand einer Leitung oder zur Leistungsanpassung eingesetzt. Anders als bei gyratorischer Kopplung bleibt bei transformatorischer Kopplung die Struktur des Netzwerkes erhalten, das heißt Reihen- und Parallelschaltungen bleiben erhalten, und induktives und kapazitives Verhalten werden nicht gegeneinander ausgetauscht.

Wenn es auf die galvanische Trennung des Transformators nicht ankommt, kann der ideale Transformator im Ersatzschaltbild nach Transformation aller sekundärseitigen Bauelemente auf die Primärseite entfallen.

Signalformen und Bandbreite

Die Speisung mit einer sinusförmigen Eingangsspannung ist typisch für Leistungstransformatoren, wie sie beispielsweise im öffentlichen Stromnetz eingesetzt werden. Die Netzfrequenz in einem Stromnetz ist durch die Umdrehungsgeschwindigkeit der Generatoren vorgegeben. Typische Werte für die Netzfrequenz sind 50 Hz (öffentliches Stromnetz in Europa) und 60 Hz (Stromnetz in den USA). In der Bahnstromversorgung gibt es darüber hinaus auch Netze mit Netzfrequenzen von 16,7 Hz und 25 Hz.

In PC-Netzteilen, Frequenzumrichtern und den Wechselrichtern der Photovoltaik werden in speziellen Schaltnetzteilen Rechteckspannungen mit wesentlich höheren Frequenzen erzeugt und transformiert. Die dabei eingesetzten Transformatoren dienen vorwiegend zur galvanischen Trennung und zur Spannungsanpassung, wobei eine Sättigung des Transformatorkerns vermieden wird.[18]

In Sperrwandlern werden zwei magnetisch gekoppelte Spulen mit einem Kern mit Luftspalt als Energiespeicher verwendet.[19] Die über die Primärseite ins magnetische Feld eingebrachte Energie wird nicht sofort entnommen, sondern erst nach Abschalten der Eingangsspannung an der Sekundärseite abgegriffen. Bei rechteckförmigen Eingangsspannungen ergeben sich somit annähernd dreieckförmige Eingangsströme.[20]

Bei der Übertragung von Signalen mit einem Transformator ist es wichtig, dass die Signalanteile aller relevanten Frequenzen übertragen werden. Bei Verwendung einer ohmschen Last weist der Transformator ein sogenanntes Bandpassverhalten auf.[21] Bei ungeeigneter Dimensionierung oder falscher Beschaltung kann ein Transformator darüber hinaus ein unerwünschtes Schwingverhalten, eine sogenannte Resonanzüberhöhung, aufweisen.

Die Begrenzung der Bandbreite nach unten kommt durch die Hauptinduktivität $L_{h1}$ zustande. Sie schließt Signale niedriger Frequenzen kurz. Nach oben erfolgt die Begrenzung der Bandbreite im Netzwerkmodell allein durch die Streuinduktivitäten $L_{\sigma 1}$ und $L_{\sigma 2}$ . Ihre Impedanz steigt mit der Frequenz und verhindert auf diese Weise eine Signalübertragung. Bei hohen Frequenzen ist außerdem die kapazitive Kopplung zwischen den einzelnen Windungen relevant.

In der Praxis ist der Frequenzbereich von Transformatoren nach unten vorwiegend durch die erforderliche Größe begrenzt, die mit sinkender Frequenz stark ansteigt. Der typische Frequenzbereich von Niederfrequenztransformatoren reicht bis 16,7 Hz hinunter, der Nennfrequenz für die Bahnstromversorgung. Am oberen Ende des Frequenzbereiches stehen Transformatoren der Hochfrequenztechnik, bei denen die Wicklungen häufig nur noch aus wenigen oder sogar nur einer einzigen Windung bestehen. Die Frequenzspanne handelsüblicher Hochfrequenztransformatoren umfasst einen Bereich von wenigen MHz bis etwa 1 GHz.[22]

Weg der Energieübertragung

Entgegen einer weitverbreiteten Vorstellung findet die Energieübertragung beim Transformator nicht über den Transformatorkern selbst, sondern über das elektromagnetische Feld im umgebenden Medium statt.[23] Der Poyntingvektor, der die Richtung des Energieflusses angibt, steht dabei senkrecht auf den elektrischen Feldlinien, die ringförmig um den Transformatorkern laufen, und den magnetischen Feldlinien des Streufeldes, die durch Primär- und Sekundärströme gebildet werden. Eine Visualisierung der Zusammenhänge findet sich im Artikel von Herrmann und Schmid.[24] Die Darstellung zeigt, dass sich sowohl in elektrischen Stromkreisen als auch in magnetischen Kreisen die Energie nie in den Leitungen selbst, sondern immer entlang der Leitungen bewegt.

Da die Energieübertragung mittels des Transformator-Streufeldes geschieht, steht die Vorstellung eines idealen Transformators ohne Streufeld streng genommen im Widerspruch zu den maxwellschen Gleichungen. Im American Journal of Physics formuliert Newcomb[25] diesen Zusammenhang folgendermaßen:

“In conclusion, let us note that there is something paradoxical in the notion of a strictly ideal transformer […]. If such a thing existed, we could reverse the foregoing arguments and conclude that both E and H must vanish in the exterior region, thus making it impossible to account for the power flow. Still, it should also be emphasized that the use of ideal-transformer relations is perfectly legitimate as an asymptotic approximation in the low-frequency limit.”

„Schlussfolgernd wollen wir festhalten, dass der Gedanke eines strikt „idealen“ Transformators eine Paradoxie enthält […]. Sollte ein solcher existieren, könnten wir die vorherigen Argumente verwerfen und stattdessen schlussfolgern, dass sowohl E als auch H im Außenbereich verschwänden, was es unmöglich machen würde, den Leistungsfluss zu bewerten. Trotzdem muss betont werden, dass die Gleichungen für ideale Transformatoren als asymptotische Näherung im niederfrequenten Bereich Gültigkeit haben.“

– William A. Newcomb[25]

In der Zeitschrift Praxis der Naturwissenschaften – Physik in der Schule (PdN-PhiS) empfiehlt Herrmann im Zusammenhang mit der Energieübertragung beim Transformator, das Feld zwischen den Schenkeln eines Transformators nicht als Streufeld zu bezeichnen, da es für den Energietransport wichtig sei. Beim Transformator solle darüber hinaus nicht nur das Feld der magn. Flussdichte, sondern auch das Feld der magnetischen Feldstärke diskutiert werden und bei möglichst vielen Gelegenheiten die Frage nach dem Weg der Energieübertragung gestellt werden.[26]

Verhalten bei Netzstörungen und beim Einschalten

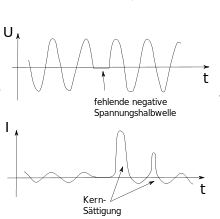
Verlauf von Strom und Spannung bei Netzstörungen am belasteten Transformator

Typisches Verhalten eines Transformators beim Einschalten. Das Maximum des Magnetisierungsstroms liegt nach der ersten Spannungshalbwelle.

Einschaltvorgänge und Netzstörungen bewirken besonders starke Abweichungen des Transformatorverhaltens vom idealen Verhalten. Beide Vorgänge können den Transformatorkern sättigen und zu beträchtlichen Überströmen führen.

Entsprechend dem Induktionsgesetz entscheidet allein der Verlauf der Eingangsspannung, ob bei einem Transformator Sättigungserscheinungen auftreten oder nicht. Der Belastungszustand spielt keine wesentliche Rolle; selbst ein Kurzschluss auf der Sekundärseite führt nicht zur Sättigung.[27]

Bei einer typischen Netzstörung im 230-V-Netz fallen vereinfacht betrachtet einzelne oder mehrere Spannungshalbwellen beziehungsweise Teile davon aus. Der Transformator reagiert auf das Ausfallen der Netzhalbwelle mit einem großen Sättigungsstrom in der darauf folgenden Halbwelle.[28] Den wesentlichen Beitrag zur Kernsättigung liefert die Vormagnetisierung des Kerns, die durch die Störung der Eingangsspannung verursacht wird.

Beim Abschalten oder Ausfall der Spannung verharrt der Magnetisierungszustand des Kerns in dem Remanenzpunkt, der der Magnetisierung im Abschaltzeitpunkt am nächsten liegt. Abhängig von Polarität und Phasenlage der wiederkehrenden Netzspannung kann das dazu führen, dass ausgehend von diesem Remanenzpunkt der verbleibende Induktionshub bis zur beginnenden Sättigung kleiner ist als die Zeitfläche der wiederkehrenden Spannungshalbwelle. Die durch die Zeitfläche der wiederkehrenden Halbwelle erzwungene Flussänderung im Kern treibt diesen in die Sättigung, wobei große Magnetisierungsströme benötigt werden.

Der ungünstigste Fall für einen Luftkern ist das Einschalten einer vollen Halbwelle, was zum 2-fachen Magnetisierungsstrom des Nennwertes führt. Der ungünstigste Fall für einen Ringkern ist das Einschalten, wenn die Remanenz bei $B=B_{\mathrm {max} }$ liegt und die Polarität der wiederkehrenden Spannung identisch ist mit der vor dem Abschalten. Diesen Verlauf zeigt die untere Prinzipskizze. Der Magnetisierungsstrom ist in diesem Fall im Wesentlichen nur noch durch die Restinduktivität und durch den ohmschen Widerstand der Primärspule und die Impedanz der Netzzuleitung begrenzt. Er kann demnach extreme Werte annehmen, weil der Transformatorkern restlos gesättigt ist und keine Magnetflussänderung mehr aufnehmen kann. Die Sättigungsmagnetisierung spielt auch beim Einschalten des Transformators eine wichtige Rolle; der Einschaltstrom kann dabei kurzzeitig ein Vielfaches des Nennstromes betragen.

Diese Einschaltvorgänge klingen in jedem Fall im Verlauf einiger Halbwellen ab, da aufgrund der Asymmetrie der Magnetisierungsströme auch die beiden gegenpoligen Spannungshalbwellen mit unsymmetrischen Spannungsabfällen behaftet sind. Das hat zur Folge, dass in der Sättigungshalbwelle stets etwas weniger Spannung zur Aufmagnetisierung zur Verfügung steht als bei der dazu gegenpoligen Spannungshalbwelle die zur Abmagnetisierung führt. Dadurch zentriert sich der Magnetisierungs-Schleifendurchlauf selbsttätig nach einigen Netzperioden, wobei die Zeitkonstante dafür aus dem Quotienten der Induktivität dividiert durch die Ohmschen Widerstände im Stromkreis errechnet werden kann. Bei sehr großen Transformatoren kann diese Zeitkonstante deshalb einige Minuten betragen.

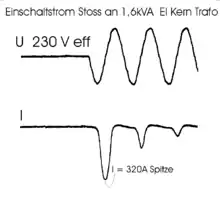
Schlienz[29] gibt als Zahlenwert für einen daraufhin optimierten 1,6-kVA-Transformator (230 V), der mit 1 kW belastet wird, einen Strom von 200 A aufgrund der Sättigung an. Im Vergleich dazu fließen im Normalbetrieb weniger als 10 A.

Anwendungen und technische Realisierung

Energietechnik

Pflanzenöl-gekühlter 380kV-Umspanner in Bruchsal

220kV/110kV-Transformator in Karlsruhe

110kV/20kV-Transformatoren am Umspannwerk Recklinghausen

5kV/20kV-Transformatoren an der Schleuse Schwabenheim

In der Energietechnik verbinden Transformatoren die verschiedenen Spannungsebenen des Stromnetzes miteinander. Maschinentransformatoren sind noch Teil der Kraftwerke und transformieren die im Generator induzierte Spannung zur Einspeisung in das Stromnetz in Hochspannung (in Westeuropa 220 kV oder 380 kV). Umspannwerke verbinden das überregionale Höchstspannungsnetz mit dem Mittelspannungsnetz der regionalen Verteilnetze. In Transformatorenstationen wird die Elektrizität des regionalen Verteilnetzes mit der Mittelspannung von 10 bis 36 kV zur Versorgung der Niederspannungsendkunden auf die im Ortsnetz verwendeten 400-V-Leiter-Leiter-Spannung transformiert. Wegen der hohen übertragenen Leistungen heißen die in der Stromversorgung verwendeten Transformatoren Leistungstransformatoren.

Leistungstransformatoren sind meist Drehstromtransformatoren, die entweder mit Transformatorenöl gefüllt oder als Trockentransformatoren ausgeführt sind. Für erstere gilt in der EU die Norm IEC (EN) 60076-1, für letztere die Norm IEC (EN) 60076-11. Parallel zu den EU-Normen existiert die IEEE-Normenreihe C57.[30]

Insbesondere in ringförmigen und mehrfach gespeisten Verteilnetzen ist es üblich, die übertragbare Leistung durch Parallelschaltung von Transformatoren zu erhöhen. Die hierzu eingesetzten Transformatoren haben gleiche Spannungsübersetzung, eine identische Schaltgruppe, nahezu gleiche Kurzschlussspannung und ähnliche Bemessungsleistungen. Das Übersetzungsverhältnis kann bei Drehstromtransformatoren, je nach Schaltgruppe, auch einen komplexen Wert annehmen, d. h., neben dem Betrag der Ausgangsspannung ändert sich auch deren Phasenlage. Zur Steuerung werden direkt in das Transformatorgehäuse Stufenschalter integriert.

Es kann zur Steuerung des Leistungsflusses notwendig sein, in räumlich ausgedehnten Verteilnetzen mit mehreren parallelen Leitungen mit unterschiedlichen Übertragungsleistungen (auch bei parallel zu Freileitungen betriebenen Kabelsystemen) spezielle Phasenschiebertransformatoren einzusetzen.

Das Transformatorprinzip findet in der Energietechnik auch in Stromwandlern Anwendung. Mit diesen werden hohe Stromstärken gemessen, indem der Strom zunächst heruntertransformiert wird. Stromwandler bestehen oft aus einem Ringkern mit Sekundärspule, der den Leiter umschließt, dessen Strom gemessen werden soll. Rogowskispulen sind wie Stromwandler aufgebaut, besitzen jedoch keinen magnetischen Kern.

Ein Tokamak, ein Kandidat für die Auslegung zukünftiger Fusionskraftwerke und Gegenstand aktueller Forschung, funktioniert ebenfalls nach dem Transformatorprinzip. In einem ringförmigen Vakuumgefäß wird eine Gasentladung herbeigeführt, indem in Leitern (Poloidalfeldspulen), die in Ringrichtung um das Gefäß angeordnet sind, der Strom langsam erhöht wird. Die Spulen bilden dabei die Primärwicklung, während das Gas im Vakuumgefäß die Sekundärwicklung darstellt.

Elektrogeräte

In Elektrogeräten, die nicht direkt mit Netzspannung arbeiten, wandeln Transformatoren die an der Steckdose anliegende Netzwechselspannung von typischerweise 230 V auf die Betriebsspannung des Elektrogeräts um.

Netzteile von Elektrogeräten enthalten entweder einen konventionellen Netztransformator, welcher mit Netzfrequenz und primärseitig (prinzipiell) direkt am Stromnetz betrieben wird, oder ein Schaltnetzteil, welches den Transformator mit einer höheren Frequenz als der Netzfrequenz betreibt. Schaltnetzteile sind heute weit verbreitet, konventionelle Netztransformatoren eher selten anzutreffen. Eine höhere Frequenz anstelle der Netzfrequenz ermöglicht bei gleicher Leistung einen wesentlich kleineren und damit leichteren Transformator und kleinere Tiefpass-Siebglieder zur Glättung der vom entsprechenden Gerät benötigten Gleichspannung.

Sicherheitstransformatoren liefern sekundärseitig eine Kleinspannung, z. B. 6 V, 12 V oder 24 V. Sie müssen kurzschlussfest sein und die Isolation der Sekundär- von der Primärwicklung muss durch eine Zwischenwand aus Isolationsmaterial sichergestellt werden. Zu den Sicherheitstransformatoren gehören Spielzeugtransformatoren wie beispielsweise Transformatoren für den Betrieb von Modelleisenbahnen und Klingeltransformatoren. Trenntransformatoren dienen primär dazu, eine galvanische Trennung zwischen Primär- und Sekundärseite zu erreichen. Sie sind daher meist symmetrisch aufgebaut, d. h., die Primärspannung entspricht der Sekundärspannung. Ist eine galvanische Trennung nicht erforderlich, können Netztransformatoren in speziellen Fällen ohne galvanische Trennung als so genannte Spartransformatoren ausgeführt sein.

Ältere Fernsehgeräte oder Computermonitore mit Kathodenstrahlröhre enthalten einen Zeilentransformator, mit dem neben der Versorgung der Zeilen-Ablenkspulen auch die für die Beschleunigung der Elektronen erforderliche Spannung (20–30 kV) erzeugt wird. Mittelfrequenztransformatoren sind für Frequenzen von einigen Hundert Hertz bis zu einigen Kilohertz ausgelegt. Sie werden beispielsweise beim Widerstandsschweißen eingesetzt.

Transformatoren mit Primärspannungen bis 1000 V unterliegen in Deutschland der ersten Verordnung zum Geräte- und Produktsicherheitsgesetz, welche die europäische Niederspannungsrichtlinie umsetzt. Sie müssen die Norm EN 61558 erfüllen, was mit der CE-Kennzeichnung dokumentiert wird. Ein Transformator mit CE-Kennzeichnung kann ohne weitere Kontrollen und Prüfungen innerhalb der EU in den Verkehr gebracht werden.

Nur selten wird ein Transformator mit der Zielsetzung verwendet, einen möglichst großen Sekundärstrom zu erzeugen (wobei dann die Sekundärspannung nachrangig ist). Dies geschieht zum Beispiel beim Elektroschweißen.

Signalübertragung

Übertrager vom Typ TG110, wie sie bei Ethernet-Schnittstellen verwendet werden

Übertrager und Pulstransformatoren sind Transformatoren, die nicht auf verlustarme Energieübertragung, sondern auf möglichst unverfälschte Transformation von Signalen optimiert sind. Jedoch gibt es auch Trafos, die z. B. zur Thyristorzündung genutzt werden, die aus Rechtecksignalen mit einigen Zusatzbauelementen, wie R-C-Dioden-Beschaltungen, kurze Zündnadelimpulse formen. Übertrager werden im Niederfrequenzbereich mit Eisenkern, bis in den Megahertzbereich mit Ferrit- oder Eisenpulverkern und ab einigen 100 kHz oft auch als Lufttransformatoren gefertigt. Sie dienen der Impedanzanpassung und/oder der galvanischen Trennung der Signalstromkreise.

In der Messtechnik werden Transformatoren zur Impedanzwandlung eingesetzt. In der Tontechnik spielen sie in jeder Stufe der Signalverarbeitung eine Rolle, so in Mikrofonen, DI-Boxen, Verstärkern und Lautsprechern. In ELA-Anlagen werden die Audiosignale meist per 100-Volt-Technik fast verlustfrei über längere Leitungen übertragen und erst direkt am Lautsprecher wieder durch einen Transformator an die Impedanz des Lautsprechers angepasst. Über die oft vorhandenen Anzapfungen der Primärwicklung lässt sich die Lautstärke (Leistung) in groben Schritten (oft 6 W, 3 W und 1,5 W) einstellen.

Bei der Signalübertragung dienen Transformatoren bis in den dreistelligen MHz-Frequenzbereich zur Gleichtaktunterdrückung. Typische Beispiele für Gleichtaktsignale, die gefiltert werden sollen, sind Spannungen, die mit gleichem Vorzeichen an beiden Übertragungsleitungen anliegen. Da Transformatoren ausschließlich die Differenz der an beiden Klemmen anliegenden Spannungen registriert, werden Gleichtaktstörungen nicht über den Transformator übertragen. In der Audiotechnik kann man auf diese Weise die sogenannten Brummschleifen verhindern. In gestörten Messumgebungen blockieren Transformatoren Störungen auf den Übertragungsleitungen, die beispielsweise durch Motoren oder Schaltnetzteile verursacht werden.

Auch in den Bandpässen der Zwischenfrequenzverstärker, z. B. für 455 kHz oder 10,7 MHz, befinden sich häufig Spulenanordnungen – oft auch noch mit Anzapfungen, die wie kleine (Spar-)Transformatoren magnetisch gekoppelt sind und die unterschiedlichen Ein- und Ausgangsimpedanzen der Transistoren anzupassen haben.

Ein ähnliches Ziel verfolgt die Symmetrische Signalübertragung, bei der ein zu übertragendes Wechselspannungssignal doppelt übertragen wird: Eine Leitung überträgt das Originalsignal, während eine zweite Leitung das mit (−1) multiplizierte Signal überträgt. Zur Generierung des Signalpaars aus einem unsymmetrischen, auf Erde bezogenen Signal wird typischerweise ein Transformator mit Mittelanzapfung verwendet. Zur Wandlung oder Rückwandlung kann auch eine auf Operationsverstärkern oder Transistoren basierende elektronische Schaltung verwendet werden.

Wirtschaftliche Aspekte

Eisenbahntransport eines Transformators mit Tragschnabelwagen

Der Weltmarkt für Transformatoren hat ein Jahresvolumen von ungefähr 10 Milliarden Euro. Er wird bisher von europäischen Gesellschaften dominiert, die jedoch zunehmend von asiatischen Unternehmen herausgefordert werden. Der größte Absatzmarkt ist China mit ungefähr 25 % des Weltmarktvolumens, gefolgt von den USA, Japan und Deutschland. In reifen Märkten wie Europa oder den USA spielen Betriebskosten und energetischer Wirkungsgrad für die Absatzchancen eines Produktes eine große Rolle, während in jüngeren Märkten wie China verstärkt über den Preis verkauft wird.[31][32]

China ist auch der größte Transformatorproduzent der Welt: 90 % der dort verkauften Transformatoren werden in diesem Land gebaut, die meisten davon von ausländischen Gesellschaften. Die weltweit führenden Hersteller von Transformatoren sind ABB und Alstom. Weitere große europäische Hersteller sind Areva, Siemens und die 2005 von Siemens übernommene VA Technologie. Die führenden Anbieter der USA sind Cooper Industries, General Electric.[31][32]

Konstruktive Details

Transformatoren gibt es von Daumennagelgröße für die Übertragung von weniger als einem Tausendstel Voltampere (VA) (zum Beispiel für Bühnenmikrophone) bis hin zu großen Einheiten mit einem Gewicht von mehreren 100 Tonnen, die für die Kopplung nationaler Stromnetze verwendet werden und für Leistungen im Bereich von mehreren Millionen Voltampere ausgelegt sind. Sie werden für zahlreiche verschiedene Zwecke eingesetzt. Entsprechend vielfältig fällt die Ausführung der Wicklungen, des Transformatorkerns und der Montage- und Befestigungselemente aus. Zur Abführung der Verlustwärme großer Leistungstransformatoren können zusätzlich bei Luftkühlung Rippenkühlkörper mit oder ohne Lüfter bzw. Kühlflüssigkeitsbehälter mit Isolieröl zum Einsatz kommen.

Transformatorenhauptgleichung

Aus dem Induktionsgesetz folgt für sinusförmige Spannungen die als Transformatorenhauptgleichung bezeichnete Beziehung:[33]

U_{\mathrm {eff} }={{\sqrt {2}}\cdot \mathrm {\pi } \cdot B_{\mathrm {max} }\cdot A\cdot f\cdot N}\!\approx 4{,}44\cdot B_{\mathrm {max} }\cdot A\cdot f\cdot N

Dabei ist $U_{\mathrm {eff} }$ der Effektivwert der Spannung, $B_{\mathrm {max} }$ die maximale magnetische Flussdichte im Kern, $A$ die Querschnittsfläche des Transformatorkerns, $f$ die Frequenz und $N$ die Windungszahl.

Bei nicht-sinusförmigen Wechselspannungen ist die Konstante ${\sqrt {2}}\cdot \mathrm {\pi }$ durch andere Werte zu ersetzen; etwa für Rechteckspannung durch $4$ und für Dreieckspannung durch $4{,}62$ .[34]

Raumbedarf und Konstruktionsparameter

Die Transformatorenhauptgleichung verbindet grundlegende Parameter eines Transformators. Die maximale magnetische Flussdichte $B_{\mathrm {max} }$ ist durch die Sättigungsmagnetisierung des Kernmaterials begrenzt. Bei gegebenen Werten der Ausgangsspannung $U_{\mathrm {eff} }$ , der Betriebsfrequenz $f$ und der maximalen magnetischen Flussdichte $B_{\mathrm {max} }$ ist das Produkt $A\cdot N$ aus Querschnittsfläche des Kerns und Windungszahl festgelegt. Diese beiden Parameter bestimmen wesentlich den Raum- und Materialbedarf eines Transformators.

Wird bei gleicher Ausgangsspannung die Betriebsfrequenz erhöht, erniedrigt sich entsprechend das Produkt $B_{\mathrm {max} }\cdot A\cdot N$ . Wird etwa ein Transformator bei 5 kHz statt bei 50 Hz betrieben, so kann das Produkt aus Windungszahl und Kernquerschnitt um einen Faktor 100 kleiner gewählt werden, was eine entsprechende Verkleinerung des Transformators bedeutet. In der Praxis wird dieses nicht ganz ausgenutzt, da sich mit höherer Frequenz auch die Hystereseverluste nach der Steinmetzformel vergrößern und deswegen bei höheren Frequenzen auch $B_{\mathrm {max} }$ etwas niedriger gewählt wird.

Höhere Betriebsfrequenzen führen also zu einem geringeren Raum- und Materialbedarf und damit auch zu einem geringeren Gewicht. Dieses ist der Grund für die geringere Baugröße von Schaltnetzteilen.

Die maximale Betriebsspannung hat auch einen kleinen Einfluss auf den Raumbedarf. Da der Kupfer-Füllfaktor aufgrund der Isolation bei steigender Speisespannung sinkt, sind Transformatoren bei gleicher Übertragungsleistung umso größer, je höher die zu verarbeitenden Spannungen sind. Die Stromdichte in den Wickeldrähten kann bei kleinen Transformatoren höher sein als bei großen, denn die Wärme kann bei jenen besser entweichen. Dementsprechend haben kleinere Transformatoren (und solche für geringere Übertragungsleistungen) üblicherweise einen kleineren Wirkungsgrad.

Material

Als Leitermaterial für die Wicklungen wird meist massiver Kupferdraht verwendet. Große Querschnitte werden in Einzelleiter aufgeteilt (Roebelstab), die gegeneinander isoliert sind und zyklisch vertauscht werden. Weiterhin kommen Folie, Band aus Weichkupfer oder Hochfrequenzlitze zum Einsatz. Bänder, Folien von Schaltnetzteiltransformatoren und Drähte von Großtransformatoren bestehen häufig aus Aluminium. Folien haben häufig nur reine Schirmfunktionen.[35]

Zur Isolierung hat der Draht eine Kunstharz-Lackierung (Kupferlackdraht) oder – früher – auch eine Umspinnung. Die dünnere Lackschicht hat ein höheres Isoliervermögen und erlaubt eine kompaktere Wicklung, als es mit umsponnenen Drähten möglich war. Relativiert wird dies bei nachfolgendem Tränken des Transformatorwickels oder beim Betrieb in Isolieröl (Transformatorenöl).

Um die Spannung zwischen benachbarten Windungen nicht allzu hoch werden zu lassen, werden Lagenisolationen eingebracht oder der Draht wird beim Wickeln in mehrere nebeneinanderliegende Kammern verlegt. Eine weitere Methode, die Spannungsfestigkeit zu erhöhen, sind Folien-Wickel. Sie werden teilweise bei Schaltnetzteil-Transformatoren, aber auch bei Großtransformatoren[36] verwendet.

Konstruktives Ziel ist eine möglichst kompakte Wicklung, um in einem durch den Kern gegebenen Wickelquerschnitt möglichst viel Kupfer oder Aluminium unterbringen zu können. Die Art der Isolierung begrenzt die mögliche Betriebstemperatur nach oben (siehe Isolierstoffklasse). Eine kompakte, möglicherweise getränkte Wicklung verbessert auch die Wärmeableitung aus dem Inneren.

Herstellung

Ein Spulenkörper (englisch coil former oder bobbin) hilft, die Wicklung in der passenden Form herzustellen und bietet zusätzliche Isolation zum Kern oder zu Nachbarwicklungen (Mehrkammer-Spulenkörper). Spulenkörper sind meist aus Kunststoffspritzguss und besitzen oft eingespritzte Kontaktstifte oder Führungen für ein- und auslaufende Wicklungsenden. Damit ist auf einer automatischen Wickelmaschine eine geordnete Wicklung möglich.

In einigen Fällen ist ein Spulenkörper zu teuer oder er schränkt den Wickelraum zu stark ein. Dann wird ein selbsttragender Wickel hergestellt und auf dem Kern mit Keilen oder anderen Zwischenlagen befestigt. Nur selten wird direkt auf die Schenkel des Transformatorkerns gewickelt, da solche Wicklungen maschinell schwer herzustellen sind und nur eine geringe Spannungsfestigkeit gegenüber dem Kern aufweisen.

Anordnung

Ein 100-VA-Trafo. Oben die Primärwicklung (230 V), unten die zwei Sekundärwicklungen (9 V).

Bei Netztransformatoren mit nur einer Wickelkammer ist die Primärwicklung meist zuunterst gewickelt – bei niedrigeren Ausgangsspannungen schützt so der meist dickere Draht der Sekundärwicklung den dünnen Draht der Primärwicklung. Bei hoher Ausgangsspannung wird durch diesen Wicklungsaufbau die Isolation zum Kern erleichtert. Das Übereinanderwickeln von Primär- und Sekundärspule wird auch Mantelwicklung genannt.

Bei Sicherheitstransformatoren sind Primär- und Sekundärwicklung in getrennten Kammern des aus Isolierstoff bestehenden Wickelkörpers untergebracht, um sie sicher voneinander zu isolieren.

Aufteilung von Primär- und Sekundärwicklung in mehrere Bereiche:

Scheibenwicklung: Anordnung der Teilwicklungen nebeneinander auf einem Schenkel des Kerns
- freitragend: Abstände zwischen den Scheiben dienen häufig als Kühlkanäle
- Mehrkammer-Wickelkörper: senkt die Lagenspannung und verringert die Eigenkapazität der Wicklung; bessere Isolation auch bei nicht getränkten Wickeln
verschachtelte Wicklungen: Audio-Transformatoren (Übertrager und Ausgangstransformatoren) haben oft unterteilte, ineinandergreifende Primär- und Sekundärwicklungen, um die Streuinduktivität zu verringern und so die Übertragung hoher Frequenzen zu verbessern.

Netz- und Signaltransformatoren besitzen eine Schirmwicklung, wenn der Ableitstrom unterbunden werden soll, der ohne Schirm von der Primärseite zur Sekundärseite durch kapazitive Kopplung der Wickel gelangt. Dieser Schirm ist an Masse angeschlossen und dient zur Verringerung der kapazitiven Kopplung zwischen Primär- und Sekundärwicklung. Der Schirm besteht aus einer einlagigen Drahtwicklung oder aus Folie, die nur an einem Ende angeschlossen ist. Die Schirmwicklung darf keine elektrisch geschlossene Schleife darstellen, weshalb die Überlappung der beiden Folienenden elektrisch isoliert sein muss. Dieser Schirm kann bei sogenannten Störschutztransformatoren auch aus hochpermeablem Material bestehen. Damit wird der Übergang von hochfrequenten Störungen zur Sekundärseite gedämpft.

Ein Transformator kann statt einer einzelnen auch mehrere getrennte Sekundärwicklungen für unterschiedliche Spannungen oder für getrennte Stromkreise haben.

Fixierung

Häufig wird die Wicklung mit Tränk- oder Gießharz fixiert. Dadurch verbessern sich die Isolation, die Wärmeableitung und die mechanische Festigkeit; das Brummen des Transformators wird reduziert und die Gefahr, dass Feuchtigkeit eindringt, wird geringer. Besonders Schaltnetzteil- und kleine Hochspannungstransformatoren werden unter Vakuum getränkt oder beim Verguss entlüftet. Dadurch werden Lufteinschlüsse beseitigt, die andernfalls zu lebensdauerverringernden Teilentladungen führen.

Anzapfungen

Dieser Transformator stammt aus einer Elektrolokomotive: Zahlreiche Anzapfungen auf der Sekundärseite, die mit Schaltern kontaktiert werden, ermöglichen den ruckfreien Anfahrbetrieb.

Die Primärwicklung kann mehrere Anzapfungen haben; damit ist ein solcher Transformator für unterschiedlich hohe Primärspannungen geeignet, wobei dennoch auf gleiche Ausgangsspannungen transformiert wird. Ein Transformator, der sowohl für den amerikanischen (120 V) als auch den europäischen Markt (230 V) einsetzbar sein soll, kann z. B. mit einer Anzapfung der Primärwicklung am Netztransformator und einem Umschalter versehen sein. Oft werden hierzu jedoch zwei Wicklungen für je 120 V aufgebracht, die wahlweise parallel oder in Reihe geschaltet werden können. Dabei kann man die geringe Spannungsabweichung zugunsten des geringeren Kupferbedarfes meistens in Kauf nehmen.

Auch die Sekundärwicklung kann Anzapfungen besitzen, um den Transformator zum Beispiel an unterschiedliche Belastungsfälle anzupassen oder mehrere Spannungen mit gleichem Bezug zu erzeugen. Die Anzapfungen können unter Last mit speziellen Lastschaltern je nach Erfordernis (Spannungs- oder Leistungsänderung) frei gewählt werden, beispielsweise bei elektrischen Lichtbogenöfen oder Bahnfahrzeugen. Eine Stromunterbrechung wird dabei durch kleine Hilfs-Stelltransformatoren vermieden.

Wird die Wicklung der Sekundärseite nach der Hälfte der Gesamtanzahl der Windungen aufgetrennt und nach außen geführt, so wird dies als Mitten- oder Mittelanzapfung bezeichnet. So stehen drei Spannungen im Verhältnis 1:1:2 zur Verfügung. Solche Transformatoren werden als Treiber- oder Ausgangsübertrager von Gegentaktendstufen sowie zur Speisung einer Zweiwege-Gleichrichtung eingesetzt. Eine solche Mittelanzapfung kann man auch schaffen, indem man zwei Wicklungen mit gleicher Anzahl von Windungen auf die Sekundärseite aufbringt und diese polrichtig in Reihe schaltet. Dadurch erhält man zwei gleiche Spannungen, die sich addieren.

Bei Stelltransformatoren kann ein beweglicher Gleitkontakt oder eine Kontaktrolle jede einzelne Windung der Ausgangswicklung kontaktieren, wodurch eine nahezu stufenlose Einstellung der Ausgangsspannung ermöglicht wird.

Material

Der Transformatorkern besteht je nach Einsatzgebiet des Transformators aus Eisen oder aus Ferriten. Einige Transformatoren haben überhaupt keinen Kern; diese bezeichnet man als Lufttransformatoren. Ferromagnetisches Material im Spulenkern hat eine wesentlich bessere magnetische Leitfähigkeit als Luft und erlaubt so einen stärkeren magnetischen Fluss, hat aber die Eigenschaft, ab bestimmten magnetischen Flussdichten zu sättigen. Bei Sättigung reduziert sich die magnetische Leitfähigkeit, was zu einem nichtlinearen Übertragungsverhalten führt.

Wirtschaftlich größte Bedeutung haben Eisenlegierungen und ferromagnetische Stähle. Für Transformatoren (Betriebsfrequenz 50 Hz oder 60 Hz) verwendet man überwiegend sogenanntes Dynamoblech nach DIN EN 10107, das aus Eisen-Silizium-Legierungen besteht. Bei Signalübertragern werden auch Nickel-Eisen-Legierungen eingesetzt. Die maximale Flussdichte liegt bei Eisen je nach Spezifikation bei 1,5 bis 2 Tesla.

Der Kern wird aus einem Stapel aus einzelnen Blechen aufgebaut, zwischen denen elektrisch isolierende Zwischenschichten liegen, wobei die Blechfläche parallel zur Richtung des magnetischen Flusses und damit senkrecht zum induzierten elektrischen Feld ist. Dadurch werden die Wirbelstromverluste reduziert. Je höher die Frequenz ist, desto dünner müssen die Bleche gewählt werden. Eine Beschädigung der Isolierung der einzelnen Blechpakete kann bei großen Transformatoren zu einer erheblichen lokalen Erwärmung des Paketes führen.

Ab Frequenzen im Kilohertzbereich würden die Wirbelstromverluste bei Eisenkernen auch bei sehr dünnen Blechen zu groß. Es werden Kerne aus amorphen oder nanokristallinen Bändern oder Ferritkerne verwendet. Ferrite haben eine hohe Permeabilität, aber nur eine geringe elektrische Leitfähigkeit. Zur Herstellung von Ferritkernen wird das meist pulverförmige Ausgangsmaterial in eine Form gegeben und unter Druck gesintert (gepresst). Hierdurch ergeben sich mehr Gestaltungsmöglichkeiten als bei den Blechpaketen, insbesondere bei der Anpassung an den Spulenkörper. Bei Ferriten liegt die maximale Flussdichte bei etwa 400 mT. Die Grenze zur Verwendung von Ferritmaterial liegt in der Herstellbarkeit im Press- und Sinterprozess. Kerne für größere Trafos werden teilweise aus Ferritblöcken zusammengesetzt. Die amorphen und nanokristallinen Kerne erlauben durch ihre natürliche Banddicke von typ. 0,02 mm die Verwendung bei höheren Frequenzen und haben sehr geringe Verluste. Typische Kernformen für diese Bänder sind Ringkerne oder seltener Schnittbandkerne.

Bauformen

Der Querschnitt des Kerns wird aus wirtschaftlichen Gründen im Bereich der Energietechnik (16…60 Hz, geblechter Eisenkern) im Verhältnis zur Windungszahl der Primärwicklung, der Betriebsspannung und der Frequenz meist so gewählt, dass die Flussdichte bei der maximal zulässigen Spannung und dabei im Leerlaufbetrieb nahe an die zulässige magnetische Sättigungsflussdichte kommt. Bei Ferritkernen und höheren Frequenzen ist das nicht möglich, weil die Verluste dann zu hoch wären. Die Aussteuerung liegt hier oft nur bei einem Zehntel der Sättigungsflussdichte.

Ringkerne

Kern aus aufgewickeltem Dynamoblech und daraus hergestellter Ringkerntrafo

Bei einem Ringkerntransformator ist ein vergleichsweise hoher Wirkungsgrad bei kleiner Baugröße möglich. Dafür ist das Wickeln der Spule aufwendiger. Ringkerne bestehen aus Blechband, Pulver oder Ferriten. Ringkerntransformatoren haben bei homogen über den Umfang verteilten Wicklungen nur ein sehr geringes Streufeld und entsprechend geringe Streuinduktivität.

Schnittbandkerne

Bei Schnittbandkernen versucht man, die Vorteile von leicht herstellbaren Drahtwickeln mit den Vorteilen eines aus Band gewickelten Kernes zu vereinen. Zur Herstellung eines Schnittbandkerns wird ein Blechband (Dicke 0,025–0,3 mm) auf einen Dorn mit rechteckigem Querschnitt aufgewickelt und verklebt. Anschließend wird der Wickel in der Mitte quer zerteilt und die Trennflächen werden poliert. Schließlich werden die Hälften in die bewickelten Spulenkörper gesteckt und verklebt. Für Schnittbandkerne werden auch texturierte Blechbänder eingesetzt.

Schnittbandkerne haben aufgrund ihrer Restluftspalte eine kleinere Remanenz als Ringkerntransformatoren und damit kleinere Einschaltströme als diese. Durch die beiden Rest-Luftspalte im Kern und dessen rechteckige Form ist die Materialausnutzung jedoch nicht so hoch wie beim Ringkerntransformator. Schnittbandkerne haben dennoch ähnlich gute Eigenschaften wie Ringkerne, die Wicklungsherstellung ist gegenüber jenen einfacher, die Schnittbandkern-Herstellung ist jedoch gegenüber anderen Kernbauformen etwas teurer.

Gestapelte Blechkerne

Transformator in Mantelbauform

Es wird zwischen Mantelbauform und Kernbauform unterschieden.[37] Bei der Einphasenausführung eines Manteltransformators befinden sich beide Windungen auf dem Mittelschenkel, entweder nebeneinander oder übereinander. Der Mittelschenkel ist in dieser Bauform durch zwei Außenschenkel ergänzt, welche je den halben Querschnitt des Mittelschenkels aufweisen, und keine Windungen tragen. Die Mantelbauform wird beispielsweise aus wechselseitig geschichteter Stapeln aus Blechen in E- und I-Form gebildet, daraus folgt die Bezeichnung EI-Kern. Eine weitere Möglichkeit sind sogenannte M-Bleche, die die gesamte Mantelform bilden und zur Montage einen Trennschnitt am Ende des Mittelschenkels haben.

Transformator in Kernbauform

Bei der Kernbauform fehlt der Mittelschenkel, der Kern bildet in Seitenansicht die Form eines Rechtecks und weist einen einheitlichen Querschnitt auf. Die Windungen befinden sich im Regelfall getrennt auf den beiden Außenschenkeln, können aber auch gemeinsam auf einem Schenkel angebracht sein. Die Kernbauform wird beispielsweise durch wechselseitig geschichtete Stapel aus Blechen in der Form eines U und I gebildet, daraus folgt die Bezeichnung UI-Kern. Eine weitere Möglichkeit sind LL-Bleche – hier wird für die Zweischenkelbauweise nur eine Blechform benötigt.

Weitere Kernbauformen

Übertrager mit Schalenkern

Insbesondere bei Ferritkernen gibt es eine Vielzahl von Bauformen, unter anderem besonders flache Ausführungen für eine bessere Wärmeableitung und solche mit zylindrischem Mittelschenkel für ein leichteres Bewickeln des Spulenkörpers. Schalen- bzw. Topfkerne weisen geringe Streufelder auf. RM-Kerne und EP-Kerne sind eine Mischform aus EE-Kern und Schalenkern.

Luftspalt

Im Regelfall ist, um die gespeicherte Energie im Kern gering zu halten, kein Luftspalt im Kern gewünscht. Man schichtet daher Bleche wechselseitig oder poliert die Grenzflächen der Kernhälften. Manche Transformatorkerne dienen jedoch der Zwischenspeicherung magnetischer Energie wie beim Sperrwandler. Dies kann durch einen Luftspalt im magnetischen Kreis erreicht werden, in dem ein wesentlicher Teil der magnetischen Feldenergie gespeichert wird. Der Feldstärkebedarf und damit der Magnetisierungsstrom steigen, die Kennlinie wird geschert beziehungsweise linearisiert. Die im Luftspalt gespeicherte magnetische Energie vergrößert die Blindleistung, wird jedoch fast verlustfrei wieder abgegeben. Die Remanenz im Kern liegt wegen der Scherung der Magnetisierungskennlinie nahe bei der Induktion Null.

Luftspalte im Kern werden auch bei Gleichstrom-Anteilen im Primärstrom wie bei Ausgangsübertragern benötigt. In sehr einfachen Schweißstromquellen erfüllen sie ebenfalls diese Funktion, denn dort wirkt der Schweißlichtbogen als Gleichrichter.[38]

Luftspalte vergrößern lokal in der Nähe des Spaltes den Streufluss, der möglicherweise dort (z. B. im Trafokessel) zu Verlusten und Störungen führt. Auch in der weiteren Umgebung besitzen solche Transformatoren oft einen erhöhten Streufluss, da ein größerer Anteil des Gesamtfeldes außerhalb des Kernes auftritt.

Luftspalte werden z. B. bei Ferritkernen und M-Blechen durch unterschiedlich lange Schenkel erreicht, bei E/I-Blechen durch gleichsinnige Stapelung und eine Zwischenlage.

Pulverkerne und Kerne aus Sintermetall besitzen einen sogenannten verteilten Luftspalt, der aus den isolierenden Schichten zwischen den Pulverkörnchen besteht. Diese Kerne vertragen daher natürlicherweise eine höhere Gleichstrom-Vormagnetisierung.

Magnetischer Nebenschluss

Streufeldtransformator 400 VA mit per Stellrad einstellbarem magnetischem Nebenschluss zur Anpassung des Ausgangsstromes (Vorschaltgerät für Leuchtröhren); unten: Primärwicklungen (220 V); oben: Sekundärwicklungen (2 × 2,5 kV, 50…80 mA); Höhe 215 mm

Durch ein zusätzliches unbewickeltes Joch mit Luftspalt wird unter anderem bei Lichtbogen-Schweißtransformatoren und Streutransformatoren (u. a. für Leuchtröhren) eine Strombegrenzung bewirkt. Das Joch dient als magnetischer Nebenschluss. Solche Transformatoren sind oft auch kurzschlussfest und besitzen im Falle von Schweißtransformatoren und manchen Leuchtröhren-Transformatoren eine mechanische Verstellmöglichkeit des Joches, sodass der abgegebene Strom eingestellt werden kann. Der magnetische Fluss in diesem Joch steigt mit dem abgegebenen Strom und kann zur Auslösung einer Überstromabschaltung herangezogen werden. Das war zum Beispiel bei Modellbahn-Transformatoren ME002 der Marke PIKO/DDR der Fall. Dort diente das Joch ausschließlich diesem Zweck und bestand lediglich aus einer Blechkonstruktion ähnlich einem Klappankerrelais. Auch Transformatoren in Mikrowellengeräten und manche Klingeltransformatoren besitzen aus diesen Gründen einen magnetischen Nebenschluss.

Masse-Leistungs-Verhältnis

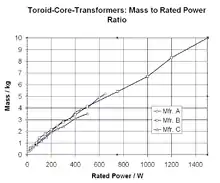
Masse-Leistungs-Verhältnis verschiedener Ringkern-Netztransformatoren dreier verschiedener Hersteller

Höhere Betriebsfrequenzen erlauben einen geringeren Materialeinsatz – siehe den Abschnitt Raumbedarf und Konstruktionsparameter. Jedoch erfordern höhere Betriebsfrequenzen oftmals aufwendigere Konstruktionen wie dünnere, teurere Bleche, Wicklungen aus Litze oder einen verschachtelten Wicklungsaufbau. Kerne aus Ferriten erlauben nur eine geringere Aussteuerung als diejenigen aus Eisen. Dennoch gelingt es mit höheren Arbeitsfrequenzen bis in den MHz-Bereich, die Baugröße und Masse von Transformatoren extrem zu verringern. So wiegt ein Ringkerntransformator für 3 kW für 50 Hz 30 kg;[39] ein Trafo gleicher Leistung für 100 kHz wiegt lediglich 0,5 kg.[40]

Netztransformatoren (50 oder 60 Hz, 115 oder 230 V) haben ein mit der Nennleistung leicht sinkendes Masse-Leistungs-Verhältnis, welches aufgrund des höheren Isolierstoffanteiles bei kleineren Transformatoren schlechter sein sollte. Andererseits können kleinere Transformatoren mit höheren Stromdichten im Wickeldraht betrieben werden (die Wärme kann besser abgegeben werden wegen geringerem Wärmeleitweg und höherer spezifischer Oberfläche), was zu einem schlechteren Wirkungsgrad führt. Daher ist das Masse-Leistungsverhältnis dennoch fast eine Gerade.

Das Masse-Leistungs-Verhältnis lässt sich durch eine hohe Induktion und damit mittels hochwertigem, bei Blechen texturiertem Kernmaterial verbessern. Ringkerntransformatoren und Schnittbandkerne sind anderen geblechten Kernen überlegen, da bei diesen die Textur immer entlang der Feldlinien gerichtet sein kann.

Geräuschentwicklung

Bei Transformatoren treten zufolge der Magnetostriktion induktionsabhängige Längenänderungen im Kernmaterial in der Größenordnung von einigen µm/m auf. Besondere Bedeutung hat dies bei Leistungstransformatoren. Die Schwingungen mit doppelter Netzfrequenz übertragen sich teilweise durch die mechanischen Verbindungen zwischen Kern und Außenumwandung und zu einem Teil durch das Öl auf die Ummantelung bzw. den Kessel des Transformators, wo sie als Schall großflächig an die Umgebung abgestrahlt werden. Zusätzlich wirken auf die Wicklungen mechanische Kräfte, die quadratisch mit dem Strom wachsen und ebenfalls Schwingungen mit doppelter Netzfrequenz erregen. Beispielsweise wird in unmittelbarer Nähe von Leistungstransformatoren mit 40 MVA, ohne die Geräuschpegel der Kühleinrichtungen, ein Geräuschpegel in der Größenordnung von 70 dB(A) erreicht.[41] Bei Umspannwerken mit Großtransformatoren in oder in der Nähe von Wohngebieten werden meist zusätzliche schalldämpfende Maßnahmen getroffen. Eine weitere Geräuschquelle des Transformators sind etwaige Pumpen und Lüfter der Kühlanlage.

Literatur

Peter Bastian, Horst Bumiller, Monika Burgmeier, Walter Eichler, Franz Huber, Jürgen Manderla, Jürgen Schwarz, Otto Spielvogel, Klaus Tkotz, Ulrich Winter, Klaus Ziegler: Fachkunde Elektrotechnik. 26., überarbeitete und erweiterte Auflage. Europa-Lehrmittel, Haan-Gruiten 2008, ISBN 978-3-8085-3160-0.
Hans Rudolf Ris: Elektrotechnik für Praktiker. 5., vollständig überarbeitete Auflage. Electrosuisse, Fehraltorf 2011, ISBN 978-3-905214-71-0 (mit CD-ROM).
Hans-Ulrich Giersch, Hans Harthus, Norbert Vogelsang: Elektrische Maschinen. 5. Auflage. Teubner, Stuttgart 2003, ISBN 3-519-46821-2.
Rudolf Janus: Transformatoren. VDE, Berlin 1993, ISBN 3-8007-1963-0.
Helmut Vosen: Kühlung und Belastbarkeit von Transformatoren. VDE, Berlin 1997, ISBN 3-8007-2225-9.
Rolf Fischer: Elektrische Maschinen. 12. Auflage. Hanser, München 2004, ISBN 3-446-22693-1.
Adolf J. Schwab: Elektroenergiesysteme – Erzeugung, Transport, Übertragung und Verteilung elektrischer Energie. Springer, 2006, ISBN 3-540-29664-6.

Weblinks

Commons: Transformatoren – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Transformator – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Wikibooks: Transformator – Lern- und Lehrmaterialien

TU-Ilmenau: Lernprogramm Transformator
National High Magnetic Field Laboratory der Florida State University: Simulation eines Transformators (Java-Applet, engl.)
Lehrgang „Grundlagen der Elektrotechnik, Transformator“ der TU Dortmund von 2003
Deutsches Kupferinstitut: Auswahl und Berechnung von Klein-Transformatoren (PDF; 682 kB)
Flash-Animation zur Funktion des Transformators (dwu-Unterrichtsmaterialien)

Einzelnachweise

NATIONAL HIGH MAGNETIC FIELD LABORATORY USA – The Stanley Transformer – 1886 (englisch)
VDE „Chronik der Elektrotechnik – Transformator“
Borns: Beleuchtung mittels sekundärer Generatoren. In: Elektrotechnische Zeitung. Nr. 5, 1884, S. 77–78
VDE-Website - Dolivo-Dobrowolsky
Gerhard Neidhöfer: Michael von Dolivo-Dobrowolsky und der Drehstrom. Anfänge der modernen Antriebstechnik und Stromversorgung. VDE-Buchreihe Geschichte der Elektrotechnik Band 9, 2. Auflage. VDE VERLAG, Berlin Offenbach, ISBN 978-3-8007-3115-2.
WEKA Media Lexikon (Memento vom 23. Juli 2012 im Webarchiv archive.today)
Friedrich Uppenborn: Geschichte der Transformatoren, München/Leipzig, 1888. Englische Übersetzung 1889 als History of The Transformer. In: Open Library ((Volltext bei Open Library))
Gisbert Kapp: Transformatoren für Wechselstrom und Drehstrom: Eine Darstellung ihrer Theorie, Konstruktion und Anwendung. Berlin, 1907 ((Volltext bei Open Library)).
Karl Küpfmüller, Wolfgang Mathis, Albrecht Reibiger: Kapitel 29.3 Der Transformator In: Theoretische Elektrotechnik, Eine Einführung. 17. Auflage, ISBN 3-540-29290-X (Auszug in der Google-Buchsuche).
H. R. Ris: Elektrotechnik für Praktiker. 1. Auflage. Buchverlag Elektrotechnik Aarau (Schweiz), 1990, ISBN 3-905214-11-3, S. 495 f.
Eckhard Spring: Elektrische Maschinen: Eine Einführung. 3. Auflage. Springer, Dordrecht/Heidelberg/London/New York 2009, ISBN 978-3-642-00884-9, 2.2 Realer Transformator, S. 115–129 (eingeschränkte Vorschau in der Google-Buchsuche).
Wolf-Ewald Büttner: Grundlagen der Elektrotechnik. 2. Auflage. Band 2. Oldenbourg, München 2009, ISBN 978-3-486-58981-8, 9.4.2 Berücksichtigung der Kernverluste, S. 294 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 8. Dezember 2012]).
Adolf J. Schwab: Elektroenergiesysteme – Erzeugung, Transport, Übertragung und Verteilung elektrischer Energie. S. 351.
H. R. Ris: Elektrotechnik für Praktiker. 1. Auflage. Buchverlag Elektrotechnik Aarau (Schweiz), 1990, ISBN 3-905214-11-3, S. 499.
DIN EN 60076-5; VDE 0532-76-5:2007-01:2007-01: Leistungstransformatoren – Teil 5: Kurzschlussfestigkeit (IEC 60076-5:2006)
H. R. Ris: Elektrotechnik für Praktiker. 1. Auflage. Buchverlag Elektrotechnik Aarau (Schweiz), 1990, ISBN 3-905214-11-3, S. 502.
Ekbert Hering: Bild 16.13. In: Grundwissen des Ingenieurs. 14. Auflage, Fachbuchverlag Leipzig, ISBN 978-3-446-22814-6, S. 780.
Joachim Specovius: Grundkurs Leistungselektronik. Vieweg, 2003, ISBN 3-528-03963-9 (Abschnitt 18.8 Durchflusswandler).
Manfred Michel: Leistungselektronik. Einführung in Schaltungen und deren Verhalten. 4. Auflage, Springer, Berlin 2009, ISBN 978-3-540-75610-1 (Abschnitt 7.2.2).
Ulrich Schlienz: Schaltnetzteile und ihre Peripherie. Dimensionierung, Einsatz, EMV. 3. Auflage, Vieweg, 2007, ISBN 3-8348-0239-5 (Kapitel 6).
E. Böhmer, D. Ehrhardt, W. Oberschelp: Elemente der angewandten Elektronik. 14. Auflage, Vieweg-Verlag, 2007, ISBN 3-528-01090-8 (Kapitel 6.2).
RF Transformers. (Nicht mehr online verfügbar.) Fa. Minicircuits, archiviert vom Original am 15. September 2011; abgerufen am 29. November 2009 (Produktübersicht).
J. Edwards, T. K. Saha: Power flow in transformers via the poynting vector. Queensland University of Technology, 2001 (Volltext (Memento vom 28. Dezember 2013 im Internet Archive; PDF; 271 kB))
F. Herrmann: The Poynting vector field and the energy flow within a transformer. In: American Journal of Physics. Band 54, Nr. 6, 1986, S. 528, doi:10.1119/1.14554 (web.archive.org [PDF; 338 kB; abgerufen am 7. September 2021]).
William A. Newcomb: Where is the Poynting vector in an ideal transformer? In: American Journal of Physics. 52, Nr. 8, 1984, S. 723–724, doi:10.1119/1.13563.
F. Herrmann: Altlasten der Physik (87) – Das Streufeld des Transformators. In: PdN-PhiS. Band 1/55, 2006 (web.archive.org [PDF; 189 kB; abgerufen am 7. September 2021]).
Adolf J. Schwab: Begriffswelt der Feldtheorie. Praxisnahe, anschauliche Einführung. Elektromagnetische Felder, Maxwellsche Gleichungen, Gradient, Rotation, Divergenz. 6. Auflage, Springer, Berlin 2002, ISBN 3-540-42018-5.
Ulrich Schlienz: Schaltnetzteile und ihre Peripherie. Dimensionierung, Einsatz, EMV. 3. Auflage. Vieweg Verlagsgesellschaft, 2001, ISBN 3-528-03935-3, Abschnitt 13.5.3 Ausfall von Netzhalbwellen.
Ulrich Schlienz: Schaltnetzteile und ihre Peripherie. Dimensionierung, Einsatz, EMV. 3. Auflage. Vieweg Verlagsgesellschaft, 2001, ISBN 3-528-03935-3, Abschnitt 13.5.4 Einschalten eines Trafos im Nulldurchgang.
IEEE-Normenreihe C57
Electronics Industry Market Research and Knowledge Network: Global Electricity Transformers Market is Expected to Exceed $36.7 Billion by 2015.3. Dezember 2008.
Goulden Reports: The world markets and manufacturers of transformers 2005–2010. (PDF; 26 kB).
H. R. Ris: Elektrotechnik für Praktiker. 1. Auflage. Buchverlag Elektrotechnik Aarau (Schweiz), 1990, ISBN 3-905214-11-3, S. 492.
Gisbert Kapp: Transformatoren für Wechselstrom und Drehstrom: Eine Darstellung ihrer Theorie, Konstruktion und Anwendung. Berlin 1907, S. 28 (Volltext bei Open Library).
Gesamtverband der Aluminiumindustrie: Aluminium in der Elektrotechnik und Elektronik, hier 3. Abschnitt (Memento vom 10. Juli 2009 im Internet Archive)
GEAFOL – Gießharz-Transformatoren Drehstrom-Verteilungstransformator. (PDF) Abgerufen am 28. Juni 2009 (Information der Siemens AG zum Einsatz von Aluminium-Folie-Wicklung bei Großtransformatoren).
Wolfgang Böge (Hrsg.): Vieweg Handbuch Elektrotechnik: Grundlagen und Anwendungen für Elektrotechniker. 4. Auflage. Vieweg+Teubner Verlag, 2007, ISBN 978-3-8348-0136-4, S. 809.
Herbert A. Fritz: Fertigungstechnik. Hrsg.: Günter Schulze. Springer, 2010, ISBN 978-3-642-12878-3., S. 162ff
http://www.tme.eu/de/Document/af2ca4e3fc2a87d5df3a187c03c9a4f7/TST10+800-4000.PDF.
2 x EILP50/64 low profile Kern.
Rolf Fischer: Elektrische Maschinen. 14. Auflage. Hanser, 2009, ISBN 978-3-446-41754-0, S. 124 bis 125.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[NHM-1] NATIONAL HIGH MAGNETIC FIELD LABORATORY USA – The Stanley Transformer – 1886 (englisch)

[VDE-2] VDE „Chronik der Elektrotechnik – Transformator“

[3] Borns: Beleuchtung mittels sekundärer Generatoren. In: Elektrotechnische Zeitung. Nr. 5, 1884, S. 77–78

[4] VDE-Website - Dolivo-Dobrowolsky

[5] Gerhard Neidhöfer: Michael von Dolivo-Dobrowolsky und der Drehstrom. Anfänge der modernen Antriebstechnik und Stromversorgung. VDE-Buchreihe Geschichte der Elektrotechnik Band 9, 2. Auflage. VDE VERLAG, Berlin Offenbach, ISBN 978-3-8007-3115-2.

[6] WEKA Media Lexikon (Memento vom 23. Juli 2012 im Webarchiv archive.today)

[7] Friedrich Uppenborn: Geschichte der Transformatoren, München/Leipzig, 1888. Englische Übersetzung 1889 als History of The Transformer. In: Open Library ((Volltext bei Open Library))

[8] Gisbert Kapp: Transformatoren für Wechselstrom und Drehstrom: Eine Darstellung ihrer Theorie, Konstruktion und Anwendung. Berlin, 1907 ((Volltext bei Open Library)).

[9] Karl Küpfmüller, Wolfgang Mathis, Albrecht Reibiger: Kapitel 29.3 Der Transformator In: Theoretische Elektrotechnik, Eine Einführung. 17. Auflage, ISBN 3-540-29290-X (Auszug in der Google-Buchsuche).

[10] H. R. Ris: Elektrotechnik für Praktiker. 1. Auflage. Buchverlag Elektrotechnik Aarau (Schweiz), 1990, ISBN 3-905214-11-3, S. 495 f.

[spring-11] Eckhard Spring: Elektrische Maschinen: Eine Einführung. 3. Auflage. Springer, Dordrecht/Heidelberg/London/New York 2009, ISBN 978-3-642-00884-9, 2.2 Realer Transformator, S. 115–129 (eingeschränkte Vorschau in der Google-Buchsuche).

[büttner-12] Wolf-Ewald Büttner: Grundlagen der Elektrotechnik. 2. Auflage. Band 2. Oldenbourg, München 2009, ISBN 978-3-486-58981-8, 9.4.2 Berücksichtigung der Kernverluste, S. 294 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 8. Dezember 2012]).

[13] Adolf J. Schwab: Elektroenergiesysteme – Erzeugung, Transport, Übertragung und Verteilung elektrischer Energie. S. 351.

[14] H. R. Ris: Elektrotechnik für Praktiker. 1. Auflage. Buchverlag Elektrotechnik Aarau (Schweiz), 1990, ISBN 3-905214-11-3, S. 499.

[15] DIN EN 60076-5; VDE 0532-76-5:2007-01:2007-01: Leistungstransformatoren – Teil 5: Kurzschlussfestigkeit (IEC 60076-5:2006)

[16] H. R. Ris: Elektrotechnik für Praktiker. 1. Auflage. Buchverlag Elektrotechnik Aarau (Schweiz), 1990, ISBN 3-905214-11-3, S. 502.

[17] Ekbert Hering: Bild 16.13. In: Grundwissen des Ingenieurs. 14. Auflage, Fachbuchverlag Leipzig, ISBN 978-3-446-22814-6, S. 780.

[18] Joachim Specovius: Grundkurs Leistungselektronik. Vieweg, 2003, ISBN 3-528-03963-9 (Abschnitt 18.8 Durchflusswandler).

[19] Manfred Michel: Leistungselektronik. Einführung in Schaltungen und deren Verhalten. 4. Auflage, Springer, Berlin 2009, ISBN 978-3-540-75610-1 (Abschnitt 7.2.2).

[20] Ulrich Schlienz: Schaltnetzteile und ihre Peripherie. Dimensionierung, Einsatz, EMV. 3. Auflage, Vieweg, 2007, ISBN 3-8348-0239-5 (Kapitel 6).

[21] E. Böhmer, D. Ehrhardt, W. Oberschelp: Elemente der angewandten Elektronik. 14. Auflage, Vieweg-Verlag, 2007, ISBN 3-528-01090-8 (Kapitel 6.2).

[22] RF Transformers. (Nicht mehr online verfügbar.) Fa. Minicircuits, archiviert vom Original am 15. September 2011; abgerufen am 29. November 2009 (Produktübersicht).

[23] J. Edwards, T. K. Saha: Power flow in transformers via the poynting vector. Queensland University of Technology, 2001 (Volltext (Memento vom 28. Dezember 2013 im Internet Archive; PDF; 271 kB))

[24] F. Herrmann: The Poynting vector field and the energy flow within a transformer. In: American Journal of Physics. Band 54, Nr. 6, 1986, S. 528, doi:10.1119/1.14554 (web.archive.org [PDF; 338 kB; abgerufen am 7. September 2021]).

[Newcomb-25] William A. Newcomb: Where is the Poynting vector in an ideal transformer? In: American Journal of Physics. 52, Nr. 8, 1984, S. 723–724, doi:10.1119/1.13563.

[26] F. Herrmann: Altlasten der Physik (87) – Das Streufeld des Transformators. In: PdN-PhiS. Band 1/55, 2006 (web.archive.org [PDF; 189 kB; abgerufen am 7. September 2021]).

[27] Adolf J. Schwab: Begriffswelt der Feldtheorie. Praxisnahe, anschauliche Einführung. Elektromagnetische Felder, Maxwellsche Gleichungen, Gradient, Rotation, Divergenz. 6. Auflage, Springer, Berlin 2002, ISBN 3-540-42018-5.

[28] Ulrich Schlienz: Schaltnetzteile und ihre Peripherie. Dimensionierung, Einsatz, EMV. 3. Auflage. Vieweg Verlagsgesellschaft, 2001, ISBN 3-528-03935-3, Abschnitt 13.5.3 Ausfall von Netzhalbwellen.

[29] Ulrich Schlienz: Schaltnetzteile und ihre Peripherie. Dimensionierung, Einsatz, EMV. 3. Auflage. Vieweg Verlagsgesellschaft, 2001, ISBN 3-528-03935-3, Abschnitt 13.5.4 Einschalten eines Trafos im Nulldurchgang.

[30] IEEE-Normenreihe C57

[electronics-31] Electronics Industry Market Research and Knowledge Network: Global Electricity Transformers Market is Expected to Exceed $36.7 Billion by 2015.3. Dezember 2008.

[gouldenreports-32] Goulden Reports: The world markets and manufacturers of transformers 2005–2010. (PDF; 26 kB).

[33] H. R. Ris: Elektrotechnik für Praktiker. 1. Auflage. Buchverlag Elektrotechnik Aarau (Schweiz), 1990, ISBN 3-905214-11-3, S. 492.

[34] Gisbert Kapp: Transformatoren für Wechselstrom und Drehstrom: Eine Darstellung ihrer Theorie, Konstruktion und Anwendung. Berlin 1907, S. 28 (Volltext bei Open Library).

[35] Gesamtverband der Aluminiumindustrie: Aluminium in der Elektrotechnik und Elektronik, hier 3. Abschnitt (Memento vom 10. Juli 2009 im Internet Archive)

[36] GEAFOL – Gießharz-Transformatoren Drehstrom-Verteilungstransformator. (PDF) Abgerufen am 28. Juni 2009 (Information der Siemens AG zum Einsatz von Aluminium-Folie-Wicklung bei Großtransformatoren).

[boege1-37] Wolfgang Böge (Hrsg.): Vieweg Handbuch Elektrotechnik: Grundlagen und Anwendungen für Elektrotechniker. 4. Auflage. Vieweg+Teubner Verlag, 2007, ISBN 978-3-8348-0136-4, S. 809.

[38] Herbert A. Fritz: Fertigungstechnik. Hrsg.: Günter Schulze. Springer, 2010, ISBN 978-3-642-12878-3., S. 162ff

[39] ttp://www.tme.eu/de/Document/af2ca4e3fc2a87d5df3a187c03c9a4f7/TST10+800-4000.PDF.

[40] 2 x EILP50/64 low profile Kern.

[41] Rolf Fischer: Elektrische Maschinen. 14. Auflage. Hanser, 2009, ISBN 978-3-446-41754-0, S. 124 bis 125.