Nichtlineares System

Nichtlineare Systeme (NL-Systeme) sind Systeme der Systemtheorie, deren Ausgangssignal nicht immer proportional zum Eingangssignal (Systemreiz) ist. Sie können wesentlich komplexer sein als lineare Systeme.

Allgemeine Grundlagen

Für nichtlineare Systeme gilt, im Gegensatz zu linearen Systemen, das Superpositionsprinzip nicht. Das heißt, man kann nicht von mehreren bekannten Systemreiz-Systemantwort-Paaren auf eine unbekannte Systemantwort zu gegebenem Systemreiz schließen. Ferner unterscheidet man die Nichtlinearität eines Systems in statische, dynamische, einwertige und mehrwertige Nichtlinearität. Da es zu nichtlinearen Systemen keine geschlossene mathematische Theorie gibt, gibt es auch keine allgemeine Methode zur Analyse unbekannter nichtlinearer Systeme.[1]

Allgemein kann man ein mathematisches Modell eines nichtlinearen Systems mit innerem Zustand $x(t)$ , äußeren Einflüssen $u(t)$ und Beobachtungen $y(t)$ darstellen als

{\begin{aligned}{\dot {x}}(t)&=A{\bigl (}t,x(t),u(t){\bigr )}\\y(t)&=C{\bigl (}t,x(t),u(t){\bigr )},\end{aligned}}

wobei $A$ und $C$ die das System beschreibenden, nichtlinearen Funktionen sind.

Statische nichtlineare Systeme

Veranschaulichung einer linearen (linkes Diagramm) gegenüber einer nichtlinearen (rechtes Diagramm) Kennlinie. Die gestrichelte Diagonale veranschaulicht die lineare bzw. nichtlineare Transformation, die schwarze Kurve ist das Eingangs-, die blaue das Ausgangssignal.

Unter statischen nichtlinearen Systemen versteht man solche, die ohne Zeitverzögerung auf einen Systemreiz reagieren. Zum Beispiel wird die Diode im Allgemeinen (Ausnahme etwa bei schnellen Schaltvorgängen) als statisches Bauteil angesehen. Ihre Spannung-Strom-Kennlinie folgt einer Exponentialfunktion; sie wird in verschiedenen Anwendungen idealisiert als stückweise linear behandelt, bleibt aber im systemtheoretischen Sinne nichtlinear. Statische Systeme können durch eine statische Kennlinie beschrieben werden, wie sie in den Abbildungen gezeigt werden.

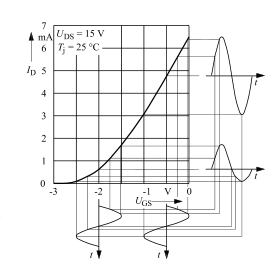
Kennlinie eines Feldeffekttransistors
Oben (so etwa bei > 3 mA) fast linear: Ein sinusförmiger Verlauf einer Änderung ΔU_GS erzeugt eine Änderung ΔI_D ohne sichtbare Abweichung vom Sinusverlauf.
Unten (so etwa bei < 3 mA) nicht linear: Ein sinusförmiger Verlauf einer Änderung ΔU_GS erzeugt eine Änderung ΔI_D mit erkennbar nicht sinusförmigem Verlauf.

Dynamische nichtlineare Systeme

Unter dynamischen nichtlinearen Systemen versteht man solche, die auch Speicherelemente und damit ein „Gedächtnis“ besitzen. Dadurch wird die Systemantwort nicht vom augenblicklichen Wert des Systemreizes allein bestimmt. Sie hängt auch von der Vorgeschichte, also von der Stärke der vorangehenden Erregung ab.[2]

Charakterisierung bezüglich des Frequenzverhaltens

Bei Erregung linearer Systeme mit einem Sinus-Signal erhält man am Ausgang wiederum ein sinusförmiges Signal derselben Frequenz, jedoch mit veränderter Phasenlage und Amplitude. Diese Eigenschaft weisen nichtlineare Systeme im Allgemeinen nicht auf. Nichtlineare Systeme können an ihrem Systemausgang Frequenzanteile aufweisen, welche im Eingangssignal nicht enthalten sind (Verzerrung).

Beispiele aus der Elektrotechnik sind:

Wenn ein nichtlinearer Verstärker mit einer einzigen Sinusspannung als Eingangsspannung gespeist wird, erzeugt er am Ausgang neben einer Sinusspannung zusätzlich Harmonische. Deren Anteile werden mit zunehmender Übersteuerung größer.
Wenn der Verstärker mit einer Überlagerung zweier oder mehrerer Sinusspannungen unterschiedlicher Frequenz gespeist wird, tritt zusätzlich Intermodulation auf, und es entstehen Kombinationsfrequenzen.
Sollen mehrere modulierte Wechselspannungen gleichzeitig verstärkt werden, kann es zu Kreuzmodulation kommen. Dann übernimmt eine Wechselspannung teilweise die Modulation der anderen (Luxemburgeffekt).

Literatur

Mathukumalli Vidyasagar: Nonlinear systems analysis SIAMm Philadelphia 2008, ISBN 978-0-89871-526-2.
Muthuswamy Lakshmanan, et al.: Nonlinear dynamics - integrability, chaos, and patterns. Springer, Berlin 2003, ISBN 3-540-43908-0.

Einzelnachweise

Holk Cruse: Biologische Kybernetik. Verlag Chemie GmbH, Weinheim 1981, ISBN 3-527-25911-2.
Dezsö Varjú: Systemtheorie. Springer-Verlag, Berlin/Heidelberg 1977, ISBN 3-540-08086-4.

Weblinks

Literatur über Nichtlineares System im Katalog der Deutschen Nationalbibliothek

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Holk Cruse: Biologische Kybernetik. Verlag Chemie GmbH, Weinheim 1981, ISBN 3-527-25911-2.

[2] Dezsö Varjú: Systemtheorie. Springer-Verlag, Berlin/Heidelberg 1977, ISBN 3-540-08086-4.