Feigenbaum-Konstante
Die beiden Feigenbaum-Konstanten δ und α sind mathematische Konstanten, die in der Chaosforschung eine wichtige Rolle spielen.
Erforschung
Der Zahlenwert von wurde erstmals 1977 von den Physikern Siegfried Großmann und Stefan Thomae publiziert. Mitchell Feigenbaum, der diese Zahl bereits 1975 beim Studium der Fixpunkte von iterierten Funktionen entdeckt hatte[1], publizierte 1978 eine Arbeit über die Universalität dieser Konstante[2]. Die Bedeutung dieser Konstanten für die Chaosforschung wird oft mit der von π für die Geometrie verglichen. Ihre Zahlenwerte lauten
Diese Zahlen treten im Zusammenhang mit nichtlinearen Systemen in Erscheinung, die in Abhängigkeit von einem Parameter reguläres oder chaotisches Verhalten zeigen. Der Übergang ins Chaos ist dabei von einem Parameterbereich mit oszillierendem Verhalten gekennzeichnet. Zum chaotischen Bereich hin nimmt dabei die Oszillationsperiode stufenweise um den Faktor zwei zu, ein Phänomen, das als Periodenverdopplung bezeichnet wird. Die zugehörigen Parameterintervalle werden mit zunehmender Periode immer kürzer. Das Verhältnis der Längen aufeinander folgender Parameterintervalle unterschiedlicher Periode strebt dabei gegen die Feigenbaum-Konstante δ.
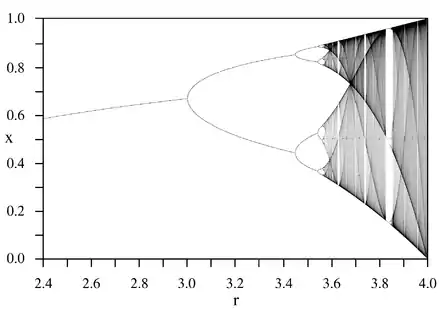
Für den Fall nichtlinearer Systeme, die durch Zahlenfolgen mit nichtlinearem rekursivem Bildungsgesetz repräsentiert werden und die in Abhängigkeit von einem Parameter ein solches Verhalten zeigen, lässt sich dieses Phänomen im so genannten Feigenbaum-Diagramm darstellen. Es stellt Folgenglieder in Abhängigkeit dieses Parameters dar und zwar ab einem Folgenindex, nach dem die Folge sich auf ein bestimmtes Verhalten eingependelt hat, wie beispielsweise Konvergenz gegen einen Grenzzyklus oder chaotisches Verhalten, und entspricht damit einer Darstellung der Häufungspunkte der Folge. Stellen, an denen eine Periodenverdopplung stattfindet, sind durch gabelförmige Strukturen gekennzeichnet, die als Bifurkationen bezeichnet werden. Das Verhältnis der Breiten aufeinander folgender Gabeln am nächsten Bifurkationspunkt strebt dabei gegen die Feigenbaum-Konstante α. Sie wird oft als zweite Feigenbaum-Konstante bezeichnet.
Im Bereich des chaotischen Verhaltens treten Inseln periodischen Verhaltens auf, „periodische Fenster“.[3] Der Übergang vom chaotischen Verhalten zu diesen Inseln nichtchaotischen Verhaltens (von links nach rechts im Diagramm) ist instantan, aus den periodischen Fenstern heraus ist der Übergang wiederum von Periodenverdopplungen gekennzeichnet, die quantitativ das gleiche Verhalten zeigen (Selbstähnlichkeit). Bénard-Zellen sind ein physikalischer Vorgang, der mit der Feigenbaum-Doppelung zu erklären ist.
Dieses qualitative Verhalten und die zugehörigen Zahlenverhältnisse hängen nicht von den Details des mathematischen oder physikalischen nichtlinearen Systems ab, sondern stellen ein universelles und damit fundamentales Gesetz derartiger Systeme dar. Das einfachste mathematische Beispiel ist das Verhalten von Zahlenfolgen quadratischen rekursiven Bildungsgesetzes wie der logistischen Gleichung und der Zahlenfolge, die der Mandelbrot-Menge zugrunde liegt.
Es wird vermutet, dass δ und α transzendent sind, ein entsprechender Beweis steht jedoch noch aus. Keith Briggs[4] entwickelte und nutzte 1991 ein Verfahren zur Berechnung der Konstanten mit erhöhter numerischer Genauigkeit. Die genauesten Werte mit 1018 Dezimalstellen wurden 1999 von David Broadhurst angegeben.[5]
Literatur
- Siegfried Großmann, Stefan Thomae: Invariant distributions and stationary correlation functions of one-dimensional discrete processes. In: Zeitschrift für Naturforschung A. 32, 1977, S. 1353–1363 (PDF, freier Volltext).
- Mitchell J. Feigenbaum: The universal metric properties of nonlinear transformations. 29. Mai 1979. In: Journal of Statistical Physics, 21, Dezember 1979, S. 669–706 (englisch; „α = 2.502907876“ auf S. 703, „δ = 4.6692“ auf S. 704) signallake.com (PDF; 1,4 MB)
- Heinz-Otto Peitgen, Peter H. Richter: The Beauty of Fractals. Springer, New York 1986, ISBN 0-387-15851-0 (englisch).
- Keith Briggs: A precise calculation of the Feigenbaum constants. In: Mathematics of Computation, 57, Juli 1991, S. 435–439 (englisch).
Weblinks
- Eric W. Weisstein: Feigenbaum Constant. In: MathWorld (englisch).
- Folge A159766 in OEIS (Kettenbruchentwicklung von δ)
- Folge A159767 in OEIS (Kettenbruchentwicklung von α)
- Numberphile: The Feigenbaum Constant (4.669) auf YouTube, 16. Januar 2017, abgerufen am 8. Februar 2020.
Einzelnachweise
- M. J. Feigenbaum: Universality in complex discrete dynamics. In: Los Alamos Theoretical Division Annual Report 1975–1976. 1976.
- Mitchell J. Feigenbaum: Quantitative universality for a class of nonlinear transformations. In: Journal of Statistical Physics. 19, Nr. 1, 1978, S. 25–52. doi:10.1007/BF01020332.
- Nichtlineare Dynamik und Chaos (PDF; 9,0 MB)
- Keith Briggs. – Homepage von Keith Briggs
- Feigenbaum constants to 1018 decimal places. In: Plouffe’s Inverter, E-Mail vom 22. März 1999