Lorenz-Attraktor

Der Lorenz-Attraktor ist der seltsame Attraktor eines Systems von drei gekoppelten, nichtlinearen gewöhnlichen Differentialgleichungen:

{\begin{aligned}{\dot {X}}&=a(Y-X)\\{\dot {Y}}&=X(b-Z)-Y\\{\dot {Z}}&=XY-cZ\end{aligned}}

Grafische Darstellung eines Lorenz-Attraktors

Formuliert wurde das System um 1963 von dem Meteorologen Edward N. Lorenz (1917–2008)[1], der es als Idealisierung eines hydrodynamischen Systems entwickelte. Basierend auf einer Arbeit von Barry Saltzman (1931–2001) ging es Lorenz dabei um eine Modellierung der Zustände in der Erdatmosphäre zum Zweck einer Langzeitvorhersage. Allerdings betonte Lorenz, dass das von ihm entwickelte System allenfalls für sehr begrenzte Parameterbereiche von $a,b,c$ realistische Resultate liefert.

Eng mit dem Lorenz-Attraktor verbunden ist das Schlagwort des Schmetterlingseffektes (Metapher aus der Chaosforschung). Das System von Differentialgleichungen stand wiederholt im Blickpunkt der Öffentlichkeit, die mit dem chaotischen Verhalten der mathematischen Gleichungen Phänomene der realen Welt zu erklären versuchte: So sollte das Lorenzsystem anschaulich machen, dass im atmosphärischen Strömungsbild kleine Ursachen große Wirkung zeigen können.

Animierter Lorenz-Attraktor; klicken zum Start der Animation

Herleitung

Zur Herleitung der Lorenzgleichung als Beschreibung von Konvektionsströmungen wurde das folgende Modell betrachtet, das um die Jahrhundertwende von dem französischen Physiker Henri Bénard experimentell untersucht und 1916 durch den britischen Nobelpreisträger Lord Rayleigh theoretisch beschrieben wurde:

Konvektionsmodell, zugeordneter Punkt im Phasenraum.

Zwischen zwei Platten mit geringem Abstand befinde sich ein viskoses inkompressibles Fluid (Flüssigkeit). Während kleine Temperaturdifferenzen zwischen der Ober- und Unterseite der Schicht noch durch Wärmeleitung ausgeglichen werden können, setzt bei Überschreiten einer kritischen Temperaturdifferenz eine Flüssigkeitsbewegung ein und es kommt zur Ausbildung von Konvektionsrollen, durch die ein effizienterer Wärmetransport realisiert wird. Dabei steigen von unten erwärmte Flüssigkeitselemente auf Grund ihrer geringeren Dichte auf und kältere Flüssigkeitsvolumina sinken ab.

Die mathematische Beschreibung des Modells durch die Navier-Stokes-Gleichungen führt über verschiedene Vereinfachungen, beispielsweise endlich abgebrochene Reihendarstellungen, zu dem oben angegebenen Gleichungssystem.

Hermann Haken zeigte, dass mit dem Lorenz-System auch Vorgänge in Lasern modelliert werden können, da das System äquivalent zu den Maxwell-Bloch-Gleichungen ist.[2]

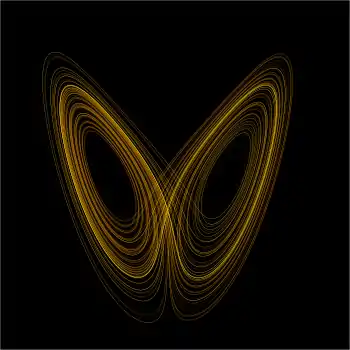
Chaostheorie

Schmetterlingsgrafik: Eine 3D-Darstellung von 2900 numerisch mittels eines Runge-Kutta-Verfahrens mit fester Schrittgröße berechneten Punkten des Lorenz-Attraktors.

Die numerische Lösung des Systems zeigt bei bestimmten Parameterwerten deterministisch chaotisches Verhalten, die Trajektorien folgen einem seltsamen Attraktor. Damit spielt der Lorenzattraktor für die mathematische Chaostheorie eine Rolle, denn die Gleichungen stellen wohl eines der einfachsten Systeme mit chaotischem Verhalten dar.

Die typische Parametereinstellung mit chaotischer Lösung lautet: $a=10,b=28$ und $c=8/3$ , wobei $a$ mit der Prandtl-Zahl und $b$ mit der Rayleigh-Zahl identifiziert werden kann.

Nach der Klärung der physikalisch-technischen Grundlagen durch die genannten Physiker und Meteorologen befassten sich in der zweiten Hälfte des 20. Jahrhunderts zahlreiche bekannte Mathematiker mit dem Problem, unter anderem der amerikanische Mathematiker John Guckenheimer. Der Beweis, dass der Lorenzattraktor ein sog. seltsamer Attraktor ist, wurde erst 1999 von dem Mathematiker Warwick Tucker erbracht[3].

Quellen

Edward N. Lorenz: Deterministic Nonperiodic Flow. In: Journal of the Atmospheric Sciences. Band 20, Nr. 2, 1. März 1963, ISSN 0022-4928, S. 130–141, doi:10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2.
H. Haken: Analogy between higher instabilities in fluids and lasers in Physics Letters 53A (1975)
Tucker, Warwick. "The Lorenz attractor exists." Comptes Rendus de l'Académie des Sciences-Series I-Mathematics 328.12 (1999): 1197-1202.

Weblinks

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Edward N. Lorenz: Deterministic Nonperiodic Flow. In: Journal of the Atmospheric Sciences. Band 20, Nr. 2, 1. März 1963, ISSN 0022-4928, S. 130–141, doi:10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2.

[2] H. Haken: Analogy between higher instabilities in fluids and lasers in Physics Letters 53A (1975)

[3] Tucker, Warwick. "The Lorenz attractor exists." Comptes Rendus de l'Académie des Sciences-Series I-Mathematics 328.12 (1999): 1197-1202.