Magnetisches Pendel

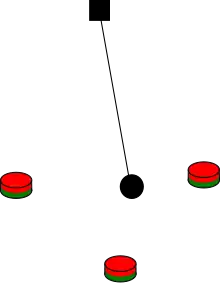
Ein magnetisches Pendel (auch: Chaospendel) besteht aus einer an einem Faden aufgehängten Eisenkugel, die über einer Anzahl am Boden befestigter Magneten hängt. Die Länge des Fadens ist dabei so gewählt, dass die Kugel die Magneten knapp nicht berühren kann. Lenkt man das Pendel aus, so führt die Kugel unter Einfluss der Schwerkraft und der magnetischen Anziehung über den Magneten Schwingungsbewegungen aus. Ist die Auslenkung und damit die Energie groß genug, so dass sich das Pendel immer wieder von der Anziehungskraft der einzelnen Magnete lösen kann, ergibt sich eine irreguläre Bewegungskurve, die empfindlich von der Anfangsposition des Pendels abhängt. Der Endzustand (Magnet 1 = rot, Magnet 2 = grün, Magnet 3 = blau) ist zwar deterministisch, das heißt, die Bewegung des Pendels ist unter der Vorgabe von Anfangsbedingungen eindeutig, da er aber sensibel von den Anfangsbedingungen abhängt, handelt es sich bei der Bewegung des Pendels um deterministisches Chaos.

Skizze eines magnetischen Pendels. Ein Fadenpendel mit einer eisernen Kugel pendelt über drei Magneten. Je nach Anfangsposition und Geschwindigkeit bleibt das Pendel im Endzustand über einem Magneten stehen.

Klassifikation des Verhaltens eines magnetischen Pendels über drei Magneten. Jede Stelle entspricht einem Startpunkt für die Pendelbewegung. Die Farbe charakterisiert den Magneten, an dem das Pendel zum Stillstand kommt. Je heller die Farbe, umso früher ist das der Fall. Die drei hellsten Stellen markieren daher die Positionen der Magnete.

Farbkarte

Das reale Magnetpendel oder das theoretische Modell mit berücksichtigten Reibungskräften kommt bei einem der Magnete zum Stillstand. Kleinste Änderungen der Anfangsposition führen das Pendel zu unterschiedlichen Magneten. Dies wird besonders deutlich, wenn man eine Karte betrachtet, bei der jeder mögliche Ausgangspunkt mit einer Farbe markiert ist, die den Magneten charakterisiert, der das Pendel schließlich einfängt. Je geringer die Reibung ist, umso filigraner werden in bestimmten Bereichen die Gebiete einer bestimmten Farbe. Siehe dazu Bild 2. Das nebenstehende Video zeigt, dass der Bereich mit chaotischen Anfangsbedingungen (d. h. Anfangsbedingungen, die bei der kleinsten Änderung zu einem unvorhersagbaren Endzustand führen) größer wird, je geringer die Reibung im Pendelsystem ist.

Mathematisches Modell

Auf die Eisenkugel wirken folgende Kräfte:

Gravitation: ${\vec {F}}_{g}=\nabla (m\,{\vec {g}}\cdot {\vec {r}})$ mit ${\vec {g}}=(0,0,-g)$ .
Anziehungskräfte der drei Magnete: ${\vec {F}}_{m}=-\nabla \sum _{i=0}^{N=3}V_{i}({\vec {r}})$ .
Reibungskräfte: Luftreibung und Lagerreibung ${\vec {F}}_{r}=-\gamma \,{\dot {\vec {r}}}$ .

Dabei ist $m$ die Masse der Eisenkugel, $g$ die Schwerebeschleunigung sowie ${\vec {r}}$ die Position der Eisenkugel. Die Magnetkraft muss aus den Potenzialen $V_{i}$ der einzelnen Magnete berechnet werden. Man kann $V_{i}={\frac {\alpha _{i}}{|{\vec {r}}-{\vec {r}}_{i}|^{b}}}$ als Potenzial annehmen, mit ${\vec {r}}_{i}$ der Position des $i$ -ten Magnets und $\alpha _{i}$ dessen Stärke und der Potenz $b$ . Die Reibung wird hier als Stokessche Reibung mit Reibungskoeffizient $\gamma$ angenommen. Aus diesen Annahmen kann eine Differentialgleichung aufgestellt werden, die die Bewegung des Pendels beschreibt:

m\,{\ddot {\vec {r}}}=\nabla (m\,{\vec {g}}\cdot {\vec {r}})-\nabla \sum _{i=0}^{N=3}V_{i}({\vec {r}})-\gamma \,{\dot {\vec {r}}}

.

Es handelt sich um ein System dreier nichtlinearer Differentialgleichungen zweiter Ordnung. Eine Lösung ${\vec {r}}(t)$ zur Anfangsbedingung $({\vec {r}}(0),{\dot {\vec {r}}}(0))$ kann nun zum Beispiel mithilfe numerischer Integration bestimmt werden.

Weblinks

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.