Proton-Proton-Reaktion

Die Proton-Proton-Reaktion (p-p-Reaktion, Proton-Proton-Kette) ist eine von zwei Fusionsreaktionen des sogenannten Wasserstoffbrennens, durch welche in Sternen Wasserstoff in Helium umgewandelt wird.

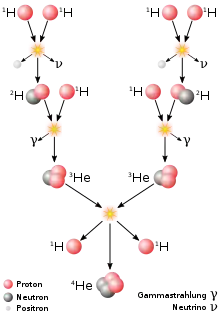
Schematischer Ablauf der Proton-Proton-I-Kette

Bei Sternen mit Massen bis etwa 1,5 Sonnenmassen (M_☉) spielt die Proton-Proton-Reaktion eine wichtigere Rolle bei der Energieumwandlung als der CNO-Zyklus.[1] Etwa werden durch sie mehr als 98 % der Leuchtkraft der Sonne erzeugt.[2]

Der stark exotherme Charakter der Fusion rührt daher, dass das Endprodukt Helium eine um etwa 0,7 % geringere Masse aufweist als die in die Reaktion eingegangenen Wasserstoffteilchen (Massendefekt).[3] Die Differenz wird dabei aufgrund der Äquivalenz von Masse und Energie ( $E=mc^{2}$ ) als Energie freigesetzt.

Die Proton-Proton-Reaktion hat die niedrigsten Temperaturvoraussetzungen aller in Sternen auftretenden Fusionsreaktionen. (In Braunen Zwergen laufen zwar auch unterhalb dieser Grenze Fusionsreaktionen ab, sie zählen aber nicht zu den Sternen.) Sie kann in Sternen mit einer Kerntemperatur von mehr als 3 Millionen Kelvin ablaufen. Bei diesen Temperaturen sind alle beteiligten Atomkerne vollständig ionisiert, d. h. ohne Elektronenhülle.

Die Fusionsrate ist bei der Proton-Proton-Reaktion proportional zur 4. Potenz der Temperatur.[4] Mithin bewirkt eine Erhöhung der Temperatur um 5 % eine Steigerung der Energiefreisetzung von 22 %.

Startreaktionen

Der erste Schritt der Proton-Proton-Reaktion: Zwei Protonen verschmelzen zu einem Deuteriumkern. Gleichzeitig werden ein Positron und ein Elektron-Neutrino emittiert.

Der zweite Schritt der Proton-Proton-Reaktion: Ein Proton und ein Deuteriumkern verschmelzen zu einem Heliumkern ³He unter gleichzeitiger Abgabe eines Gammaquants.

Der dritte Schritt der Proton-Proton-I-Kette: Zwei ³He-Kerne fusionieren zu ⁴He und setzen dabei zwei Protonen frei.

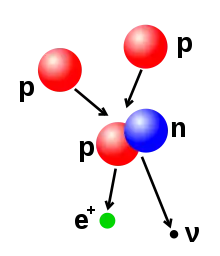
Zunächst fusionieren zwei Wasserstoffkerne ¹H (Protonen) zu einem Deuteriumkern ²H, wobei durch die Umwandlung eines Protons in ein Neutron, ein Positron e⁺ und ein Elektron-Neutrino ν_e frei werden:

\mathrm {{}^{1}H+{}^{1}H\to {}^{2}H+e^{+}+\nu _{e}+0{,}42\;MeV}

Die Kernreaktionsrate ist sehr klein und damit für die Gesamtreaktion geschwindigkeitsbestimmend. Grund ist, dass die elektrostatische Abstoßung die positiv geladenen Protonen meist auf Abstand hält, für das Diproton kein gebundener Zustand existiert und die Entstehung des Neutrons als Prozess der schwachen Wechselwirkung nur bei sehr kleinen Abständen möglich ist. Selbst nach der Maxwell-Boltzmann-Verteilung sehr seltene, besonders energiereiche Stöße reichen nach der klassischen Theorie nicht aus. Nur durch den quantenmechanischen Tunneleffekt kommen sich die Protonen doch nahe genug, allerdings mit sehr geringer Wahrscheinlichkeit: In der Sonne dauert es im Schnitt 1,4 · 10¹⁰ Jahre, bis ein bestimmtes Proton mit einem anderen reagiert, weshalb die Sonne eine große Lebensdauer hat.

Von der relativ geringen Energiefreisetzung der Reaktion trägt das Neutrino durchschnittlich 0,267 MeV davon.[5] Da diese leichten Teilchen die Sternmaterie nahezu ungehindert verlassen können, geht dieser Energieanteil dem Stern verloren.

Das entstandene Positron annihiliert sofort mit einem Elektron e⁻, d. h., sie reagieren miteinander und werden vollständig in Energie umgewandelt. Die Masse beider Partner wird in Form von zwei Gammaquanten γ als Energie frei.

\mathrm {e^{+}+e^{-}\to 2\gamma +1{,}022\;MeV}

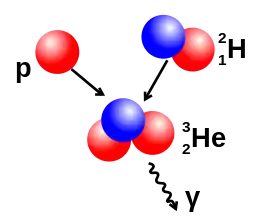
Das entstandene Deuterium kann anschließend mit einem weiteren Proton reagieren, wobei das leichte Helium-Isotop ³He entsteht:

\mathrm {{}^{2}H+{}^{1}H\to {}^{3}He+\gamma +5{,}493\;MeV}

Dieser Prozess hängt nicht von der schwachen Wechselwirkung ab, und die Bindungsenergie ist groß. Daher ist die Reaktionsrate viel größer: In der Sonne lebt das durch die Startreaktion entstandene Deuterium nur etwa 1,4 Sekunden. Das bei der Sternentstehung vorhandene Deuterium kann schon in viel kleineren Himmelskörpern reagieren, ab einer Größe von etwa 12 Jupitermassen. Dies markiert die Untergrenze für einen Braunen Zwerg.

Hauptfolgereaktionen

Es gibt nun im Wesentlichen drei verschiedene Reaktionsketten, bei denen schließlich das (in der Natur überwiegende) Helium-Isotop ⁴He erzeugt wird. Sie setzen bei verschiedenen Temperaturen ein. In der Sonne treten die nachfolgend beschriebenen Reaktionen unterschiedlich häufig auf:[6]

Proton-Proton-I-Kette: 83,30 %
Proton-Proton-II-Kette: 16,68 %
Proton-Proton-III-Kette: 0,02 %

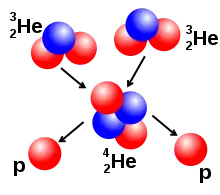
Proton-Proton-I-Kette

Nach durchschnittlich 10⁶ Jahren fusionieren zwei Heliumkerne ³He zu ⁴He (α-Teilchen), wobei zwei Protonen freiwerden. Sie stehen für weitere Reaktionsschritte zur Verfügung.

\mathrm {{}^{3}He+{}^{3}He\to {}^{4}He+2\,{}^{1}H+12{,}86\;MeV}

Die vollständige Reaktionskette bis hier, bei der die unter Startreaktion aufgeführten Reaktionen je zweimal durchlaufen werden, um die notwendigen ³He-Teilchen für die letzte Fusion zu schaffen, setzt eine Nettoenergie – also abzüglich der Neutrinoenergie – von

\mathrm {2\cdot (0{,}42\;MeV+1{,}022\;MeV+5{,}493\;MeV-0{,}267\;MeV)+12{,}86\;MeV=\mathbf {26{,}196\;MeV} }

frei (≈ 4,20 · 10⁻¹² J). Die Proton-Proton-I-Kette herrscht bei Temperaturen von 10–14 Millionen Kelvin vor. Unterhalb dieser Temperatur wird nur sehr wenig ⁴He produziert.

Proton-Proton-II-Kette

Proton-Proton-II-Kette

Bei der Proton-Proton-II-Kette dient ein früher erzeugter Heliumkern ⁴He als Katalysator, um einen weiteren aus ³He herzustellen.

{\begin{aligned}{\rm {{}^{3}He+{}^{4}He}}&\to {\rm {{}^{7}Be+\gamma +1{,}59\;MeV}}\\{\rm {{}^{7}Be+e^{-}}}&\to {\rm {{}^{7}Li+\nu _{e}+0{,}862\;MeV}}\\{\rm {{}^{7}Li+{}^{1}H}}&\to {\rm {2\,{}^{4}He+17{,}35\;MeV}}\end{aligned}}

Die Proton-Proton-II-Kette läuft vorrangig bei Temperaturen von 14–23 Millionen Kelvin ab.

89,7 % der Neutrinos, die in der Sonne durch die zweite Reaktion erzeugt werden, besitzen eine Energie von etwa 0,863 MeV, während es bei den übrigen 10,3 % etwa 0,386 MeV sind,[5] abhängig davon, ob sich das entstandene Lithium ⁷Li im Grundzustand oder im angeregten Zustand befindet.

Der dritte Reaktionsschritt kann auch ohne die beiden ersten Reaktionen mit Lithium ablaufen, das der Stern bei seiner Entstehung mitbekam (Lithiumbrennen). Dadurch nimmt die Lithiumkonzentration in Sternen ab.

Proton-Proton-III-Kette

Proton-Proton-III-Kette

Auch hier fungiert ein Heliumkern ⁴He als Katalysator.

{\begin{aligned}{\rm {{}^{3}He+{}^{4}He}}&\to {\rm {{}^{7}Be+\gamma +1{,}59\;MeV}}\\{\rm {{}^{7}Be+{}^{1}H}}&\to {\rm {{}^{8}B+\gamma +0{,}14\;MeV}}\\{\rm {{}^{8}B}}&\to {\rm {{}^{8}Be+e^{+}+\nu _{e}+18\;MeV}}\\{\rm {{}^{8}Be}}&\leftrightarrow {\rm {2\,{}^{4}He}}\end{aligned}}

Die Proton-Proton-III-Kette ist vorherrschend bei Temperaturen über 23 Millionen Kelvin.

Diese Reaktion ist zwar nicht die Hauptenergiequelle der Sonne, deren Temperatur nicht hoch genug dafür ist, sie spielt aber bei der Erklärung des solaren Neutrinoproblems eine wichtige Rolle, da sie Neutrinos mit relativ hohen Energien von bis zu 14,06 MeV erzeugt (durchschnittlich etwa 6,735 MeV[5]), die sogenannten ⁸B-Neutrinos. Solche Neutrinos lassen sich in irdischen Neutrinodetektoren leichter nachweisen als die niederenergetischen.

Weitere Reaktionen

Neben den drei vorgenannten Reaktionen gibt es noch zwei seltener ablaufende.

Proton-Elektron-Proton-Reaktion

Bei der Proton-Elektron-Proton-Reaktion, kurz pep-Reaktion, fusionieren zwei Protonen und ein Elektron zu einem Deuteriumkern.

\mathrm {{}^{1}H+e^{-}+{}^{1}H\to {}^{2}H+\nu _{e}}

Die Reaktion tritt deswegen so selten auf – in der Sonne findet die konkurrierende Reaktion ¹H + ¹H → ²H + e⁺ + ν_e etwa 400 mal so häufig statt[6] –, da hier drei Teilchen nahezu simultan zusammentreffen müssen. Die Energie der erzeugten Neutrinos ist allerdings mit etwa 1,445 MeV deutlich höher.[5]

Helium-Proton-Reaktion

Noch seltener tritt die Helium-Proton-Reaktion (kurz Hep-Reaktion) ein, die direkte Fusion von Helium ³He mit einem Proton zu ⁴He.

\mathrm {{}^{3}He+{}^{1}H\to {}^{4}He+\nu _{e}+e^{+}+18{,}77\;MeV}

Die bei dieser Reaktion emittierten Neutrinos können eine Energie von bis zu 18,778 MeV aufweisen; durchschnittlich besitzen sie eine Energie von 9,628 MeV.[5]

Asche

Die „Asche“ des Wasserstoffbrennens ist Helium ⁴He, das als Ausgangsstoff beim unter Umständen später einsetzenden Heliumbrennen dienen kann.

Siehe auch

Nukleosynthese

Weblinks

Commons: Proton-Proton-Reaktion – Sammlung von Bildern, Videos und Audiodateien

tim-thompson.com: Solar Fusion & Neutrinos

Einzelnachweise

G. Bellini et al.: First Evidence of pep Solar Neutrinos by Direct Detection in Borexino. In: Physical Review Letters. Band 108, Nr. 5, 2012, S. 051302-2, doi:10.1103/PhysRevLett.108.051302.
John N. Bahcall, M. H. Pinsonneault, Sarbani Basu: Solar Models: Current Epoch and Time Dependences, Neutrinos, and Helioseismological Properties. In: Astrophysical Journal. Band 555, Nr. 2, 2001, S. 990–1012, hier: 995, doi:10.1086/321493.
Alfred Weigert, Heinrich Johannes Wendker, Lutz Wisotzki: Astronomie und Astrophysik : ein Grundkurs. 5., aktualisierte und erw. Auflage. Wiley-VCH, Weinheim 2009, ISBN 978-3-527-40793-4, S. 215.
Eric G. Adelberger et al.: Solar fusion cross sections. II. The pp chain and CNO cycles. In: Reviews of Modern Physics. Band 83, Nr. 1, 2011, S. 195–245, hier: 226, doi:10.1103/RevModPhys.83.195.
John N. Bahcall: Gallium solar neutrino experiments: Absorption cross sections, neutrino spectra, and predicted event rates. In: Physical Review C. Band 56, Nr. 6, 1997, S. 3391–3409, doi:10.1103/PhysRevC.56.3391.
Eric G. Adelberger et al.: Solar fusion cross sections. II. The pp chain and CNO cycles. In: Reviews of Modern Physics. Band 83, Nr. 1, 2011, S. 195–245, hier: 201, doi:10.1103/RevModPhys.83.195.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] G. Bellini et al.: First Evidence of pep Solar Neutrinos by Direct Detection in Borexino. In: Physical Review Letters. Band 108, Nr. 5, 2012, S. 051302-2, doi:10.1103/PhysRevLett.108.051302.

[2] John N. Bahcall, M. H. Pinsonneault, Sarbani Basu: Solar Models: Current Epoch and Time Dependences, Neutrinos, and Helioseismological Properties. In: Astrophysical Journal. Band 555, Nr. 2, 2001, S. 990–1012, hier: 995, doi:10.1086/321493.

[3] Alfred Weigert, Heinrich Johannes Wendker, Lutz Wisotzki: Astronomie und Astrophysik : ein Grundkurs. 5., aktualisierte und erw. Auflage. Wiley-VCH, Weinheim 2009, ISBN 978-3-527-40793-4, S. 215.

[4] Eric G. Adelberger et al.: Solar fusion cross sections. II. The pp chain and CNO cycles. In: Reviews of Modern Physics. Band 83, Nr. 1, 2011, S. 195–245, hier: 226, doi:10.1103/RevModPhys.83.195.

[DOI10.1103/PhysRevC.56.3391-5] John N. Bahcall: Gallium solar neutrino experiments: Absorption cross sections, neutrino spectra, and predicted event rates. In: Physical Review C. Band 56, Nr. 6, 1997, S. 3391–3409, doi:10.1103/PhysRevC.56.3391.

[:0-6] Eric G. Adelberger et al.: Solar fusion cross sections. II. The pp chain and CNO cycles. In: Reviews of Modern Physics. Band 83, Nr. 1, 2011, S. 195–245, hier: 201, doi:10.1103/RevModPhys.83.195.