IEEE 754

Die Norm IEEE 754 (ANSI/IEEE Std 754-1985; IEC-60559:1989 – International version) definiert Standarddarstellungen für binäre Gleitkommazahlen in Computern und legt genaue Verfahren für die Durchführung mathematischer Operationen, insbesondere für Rundungen, fest. Der genaue Name der Norm ist englisch IEEE Standard for Binary Floating-Point Arithmetic for microprocessor systems (ANSI / IEEE Std 754-1985).

Die aktuelle Ausgabe ist unter der Bezeichnung ANSI / IEEE Std 754-2019[1] im Juli 2019 veröffentlicht worden. Weiter ist die Norm IEEE 854-1987, mit dem engl. Titel Standard for radix-independent floating-point arithmetic, in der IEEE 754-2008 vollständig integriert worden.[2]

Überblick

In der Norm IEEE 754-1989 werden zwei Grunddatenformate für binäre Gleitkommazahlen mit 32 Bit (single precision) bzw. 64 Bit (double precision) Speicherbedarf und zwei erweiterte Formate definiert. Die IEEE 754-2008 umfasst die binären Zahlenformate mit 16 Bit als Minifloat, 32 Bit als single, 64 Bit als double und neu 128 Bit. Zusätzlich kamen noch die dezimalen Darstellungen mit 32 Bit als Minifloat, 64 und 128 Bit hinzu.

Schließlich gab es Vorschläge und Implementierungen von weiteren Zahlenformaten, die nach den Prinzipien der IEEE 754-1989 Norm gestaltet sind und deshalb oft als IEEE-Zahlen bezeichnet werden, obwohl sie das nach der alten Definition streng genommen nicht sind. Dazu gehören die in den neuen Ausgaben integrierten Minifloats, die für die Ausbildung gedacht sind. Minifloats mit 16 Bit werden gelegentlich in der Grafikprogrammierung verwendet. Ebenso gehören auch mehrere nicht von IEEE 754-1989 definierte Zahlenformate mit mehr als 64 Bit, etwa das 80-Bit-Format (Extended Precision ^Layout...), welches die IA-32-Prozessoren intern in ihrer klassischen Gleitkommaeinheit (Floating Point Unit, FPU) verwenden, dazu.

Allgemeines

Die Darstellung einer Gleitkommazahl

x=s\cdot m\cdot b^{e}

besteht aus:

Vorzeichen $s$ (1 Bit)
Mantisse $m$ ( $p$ Bits)
Basis $b$ (bei normalisierten Gleitkommazahlen nach IEEE 754 ist $b=2$ )
Exponent $e$ ( $r$ Bits)

Das Vorzeichen $s=(-1)^{S}$ wird in einem Bit $S$ gespeichert, sodass $S=0$ positive Zahlen und $S=1$ negative Zahlen markiert.

Der Exponent $e$ wird als nichtnegative Binärzahl $E$ ( $E$ wird manchmal auch als Charakteristik oder biased exponent bezeichnet) gespeichert, indem man den festen Biaswert $B$ addiert: $E=e+B$ . Der Biaswert (engl: Verzerrung) berechnet sich durch $2^{r-1}-1$ . Der Biaswert $B$ dient also dazu, dass negative Exponenten durch eine vorzeichenlose Zahl (die Charakteristik $E$ ) gespeichert werden können, unter Verzicht auf alternative Kodierungen wie z. B. das Zweierkomplement (vergleiche auch Exzesscode).

Schließlich ist die Mantisse $1\leq m<2$ ein Wert, der sich aus den $p$ Mantissenbits mit dem Wert $M$ als $m=1+M/2^{p}$ berechnet. Einfacher ausgedrückt denkt man sich an das Mantissenbitmuster $M$ links eine „1,“ angehängt: $m=1{,}M$ .

$s=(-1)^{S}$
$e=E-B$
$m=1,M=1+M/2^{p}$

Dieses Verfahren ist möglich, weil durch Normalisierung (s. u.) die Bedingung $1\leq m<2$ für alle darstellbaren Zahlen immer eingehalten werden kann. Da dann die Mantisse immer links mit „1,“ beginnt, braucht dieses Bit nicht mehr gespeichert zu werden. Damit gewinnt man ein zusätzliches Bit Genauigkeit.

Für Sonderfälle sind zwei Exponentenwerte mit speziellen Bitmustern reserviert, der Maximalwert ( $E=11\dots 111_{2}=2^{r}-1$ ) und der Minimalwert ( $E=00\dots 000_{2}=0$ ). Mit dem maximalen Exponentenwert werden die Sonderfälle NaN und ∞ kodiert. Mit Null im Exponenten werden die Gleitkommazahl 0 und alle denormalisierten Werte kodiert.

Werte außerhalb des normalen Wertebereichs (zu große bzw. zu kleine Zahlen) werden durch ∞ bzw. −∞ dargestellt. Diese Erweiterung des Wertebereichs erlaubt auch im Falle eines arithmetischen Überlaufs häufig ein sinnvolles Weiterrechnen. Neben der Zahl 0 existiert noch der Wert −0. Während ${\tfrac {1}{0}}$ das Ergebnis ∞ liefert, ergibt ${\tfrac {1}{-0}}$ den Wert −∞. Bei Vergleichen wird zwischen 0 und −0 nicht unterschieden.

Die Werte NaN (für engl. „not a number“, „keine Zahl“) werden als Darstellung für undefinierte Werte verwendet. Sie treten z. B. auf als Ergebnisse von Operationen wie ${\tfrac {0}{0}}$ oder $\infty -\infty$ auf. NaN werden in Signal-NaN (signalling NaN, NaNs) für Ausnahmebedingungen und stille NaN (quiet NaN, NaNq) unterteilt.

Als letzter Sonderfall füllen denormalisierte Zahlen (in IEEE 754r als subnormale Zahlen bezeichnet) den Bereich zwischen der betragsmäßig kleinsten normalisierten Gleitkommazahl und Null. Sie werden als Festkommazahlen gespeichert und weisen nicht dieselbe Genauigkeit auf wie die normalisierten Zahlen. Konstruktionsbedingt haben die meisten dieser Werte den Kehrwert ∞.

Zahlenformate und andere Festlegungen des IEEE-754-Standards

IEEE 754 unterscheidet vier Darstellungen: einfach genaue (single), erweiterte einfach genaue (single extended), doppelt genaue (double) und erweiterte doppelt genaue (double extended) Zahlenformate. Bei den erweiterten Formaten ist nur jeweils eine Mindestbitzahl vorgeschrieben. Die genaue Bitzahl und der Biaswert bleiben dem Implementierer überlassen. Die Grundformate sind vollständig definiert.

Vor allem die Anzahl der Exponentenbits legt Maximum und Minimum der darstellbaren Zahlen fest. Die Anzahl der Mantissenbits bestimmt die (relative s. u.) Genauigkeit dieser Zahlen (und nur in geringem Maß das Maximum und das Minimum).

Typ	Größe (1+r+p)	Exponent (r)	Mantisse (p)	Werte des Exponenten (e)	Biaswert (B)
single	32 bit	8 bit	23 bit	−126 ≤ e ≤ 127	127
single extended	≥ 43 bit	≥ 11 bit	≥ 31 bit	e_min ≤ −1022 e_max ≥ 1023	nicht spezifiziert
double	64 bit	11 bit	52 bit	−1022 ≤ e ≤ 1023	1023
double extended	≥ 79 bit	≥ 15 bit	≥ 63 bit	e_min ≤ −16382 e_max ≥ 16383	nicht spezifiziert
quadruple	128 bit	15 bit	112 bit	−16382 ≤ e ≤ 16383	16383

Die beiden letzten Beispiele zeigen ein minimales erweitertes Format.

Für die angegebenen Formate ergibt sich die folgende Beschränkung des jeweiligen Zahlenbereichs. Die betragsmäßig kleinsten Zahlen sind hierbei nicht normalisiert. Der relative Abstand zweier Gleitkommazahlen ist größer als $\epsilon$ und kleiner gleich $2\epsilon$ . Konkret ist der Abstand (und in diesem Fall auch der relative Abstand) der Gleitkommazahl $1$ zur nächstgrößeren Gleitkommazahl gleich $2\epsilon$ . Dezimalstellen beschreibt die Anzahl der Stellen einer Dezimalzahl, die ohne Genauigkeitsverlust gespeichert werden können. Die Mantisse ist rechnerisch durch das implizite Bit um eins größer als gespeichert.

Typ	$\epsilon$	Dezimal- stellen	(betragsmäßig) kleinste Zahl (normalisiert)	(betragsmäßig) kleinste Zahl (denormalisiert)	Größte Zahl
single	2^−(23+1) ≈ 6,0·10⁻⁸	7 … 8	2⁻¹²⁶ ≈ 1,2·10⁻³⁸	2⁻²³ × 2⁻¹²⁶ ≈ 1,4·10⁻⁴⁵	(2−2⁻²³) × 2¹²⁷ ≈ 3,4·10³⁸
single extended, minimum	2^−(31+1) ≈ 2,3·10⁻¹⁰	9 … 10	2⁻¹⁰²² ≈ 2,2·10⁻³⁰⁸	2⁻³¹ × 2⁻¹⁰²² ≈ 1,0·10⁻³¹⁷	(2−2⁻³¹) × 2¹⁰²³ ≈ 1,8·10³⁰⁸
double	2^−(52+1) ≈ 1,1·10⁻¹⁶	15 … 16	2⁻¹⁰²² ≈ 2,2·10⁻³⁰⁸	2⁻⁵² × 2⁻¹⁰²² ≈ 4,9·10⁻³²⁴	(2−2⁻⁵²) × 2¹⁰²³ ≈ 1,8·10³⁰⁸
double extended, minimum	2^−(63+1) ≈ 5,4·10⁻²⁰	19 … 20	2⁻¹⁶³⁸² ≈ 3,4·10⁻⁴⁹³²	2⁻⁶³ × 2⁻¹⁶³⁸² ≈ 3,7·10⁻⁴⁹⁵¹	(2−2⁻⁶³) × 2¹⁶³⁸³ ≈ 1,2·10⁴⁹³²

Single in big-endian Darstellung

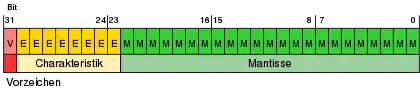
Die Anordnung der Bits einer single zeigt die nebenstehende Abbildung. Die bei einer Rechenanlage konkrete Anordnung der Bits im Speicher kann von diesem Bild abweichen und hängt von der jeweiligen Bytereihenfolge (little-/big-endian) und weiteren Rechnereigenheiten ab.

Die Anordnung mit Vorzeichen – Exponent – Mantisse in genau dieser Reihenfolge bringt (innerhalb eines Vorzeichenbereiches) die dargestellten Gleitkommawerte in dieselbe Reihenfolge wie die durch dasselbe Bitmuster darstellbaren Ganzzahlwerte. Damit können für die Vergleiche von Gleitkommazahlen dieselben Operationen wie für die Vergleiche von ganzen Zahlen verwendet werden. Kurz: die Gleitkommazahlen können lexikalisch sortiert werden.

Hierbei ist jedoch zu beachten, dass für steigende negative Ganzzahlwerte der entsprechende Gleitkommawert gegen minus unendlich geht, die Sortierung also umgekehrt ist.

Beispiele

Berechnung Dezimalzahl → IEEE754-Gleitkommazahl

Die Zahl ${\textstyle 18{,}4}$ soll in eine Gleitkommazahl umgewandelt werden, dabei nutzen wir den Single IEEE-Standard.

Umwandlung der Dezimalzahl in eine duale Festkommazahl ohne Vorzeichen
${\begin{array}{ccc}18\div 2=9&{\text{Rest 0}}&{\text{(Least-Significant Bit)}}\\9\div 2=4&{\text{Rest 1}}&\\4\div 2=2&{\text{Rest 0}}&\\2\div 2=1&{\text{Rest 0}}&\\1\div 2=0&{\text{Rest 1}}&{\text{(Most-Significant Bit)}}\\&18=10010_{2}\end{array}}$

${\begin{array}{ccc}0{,}4\cdot 2=0{,}8&-0&{\text{(Most-Significant Bit)}}\\0{,}8\cdot 2=1{,}6&-1&\\0{,}6\cdot 2=1{,}2&-1&\\0{,}2\cdot 2=0{,}4&-0&\\0{,}4\cdot 2=0{,}8&-0&\\0{,}8\cdot 2=1{,}6&-1&{\text{(Least-Significant Bit)}}\\\ldots &&\\&0{,}4=0{,}011001\ldots _{2}\end{array}}$

also $18{,}4=10010{,}011001\ldots _{2}=(1\cdot 2^{4}+0\cdot 2^{3}+0\cdot 2^{2}+1\cdot 2^{1}+0\cdot 2^{0})+(0\cdot 2^{-1}+1\cdot 2^{-2}+1\cdot 2^{-3}+0\cdot 2^{-4}+0\cdot 2^{-5}+1\cdot 2^{-6}+\ldots )$
Normalisieren und bestimmen des Exponenten
Ausklammern der höchsten Zweierpotenz: ${\textstyle (1\cdot 2^{0}+0\cdot 2^{-1}+0\cdot 2^{-2}+1\cdot 2^{-3}+0\cdot 2^{-4}+0\cdot 2^{-5}+1\cdot 2^{-6}+1\cdot 2^{-7}+0\cdot 2^{-8}+0\cdot 2^{-9}+1\cdot 2^{-10}+\ldots )\cdot 2^{4}}$
Der Bias-Wert für den Exponenten setzt sich aus einer Null und ${\textstyle r-1}$ Einsen zusammen. Für ${\textstyle r=8}$ gilt also: ${\textstyle B=01111111_{2}=127_{10}}$
Der Exponent der Zweierpotenz ${\textstyle 2^{4}}$ wird mit dem Bias B damit als ${\textstyle 4+127=131=10000011_{2}}$ hinterlegt.

Die Normalisierung von $10010,011001\ldots _{2}$ lässt sich genauso durch Kommaverschiebung im Binärsystem erreichen:
${\begin{aligned}10010{,}011001\ldots \cdot 2^{01111111-01111111}\\=1001{,}0011001\ldots \cdot 2^{10000000-01111111}\\=100{,}10011001\ldots \cdot 2^{10000001-01111111}\\=10{,}010011001\ldots \cdot 2^{10000010-01111111}\\=1{,}0010011001\ldots \cdot 2^{10000011-01111111}\end{aligned}}$

Die Mantisse ist also ${\textstyle 1{,}0010011001\ldots }$ und der Exponent mit Bias ${\textstyle 10000011}$ .
Vorzeichen-Bit bestimmen
Hier positiv, also $0$ .
Die Gleitkommazahl bilden
${\begin{array}{ccc}{\text{ 1 Bit Vorzeichen}}&{\text{8 Bit Exponent}}&{\text{23 Bit Mantisse}}\\0&10000011&00100110011001100110011\end{array}}$
Die Vorkomma-Eins der Mantisse wird als Hidden Bit weggelassen.

Berechnung IEEE754-Gleitkommazahl → Dezimalzahl

Nun soll die Gleitkommazahl von oben wieder in eine Dezimalzahl zurück gewandelt werden, gegeben ist also folgende IEEE754-Zahl
$0\ 10000011\ 00100110011001100110011$

Berechnung des Exponenten Umwandeln des Exponenten in eine Dezimalzahl
$10000011_{2}=131_{10}$
Da das Exponentenwert plus der Bias ist, wird der Bias abgezogen: $131-127=4$ ist also der Exponent.
Berechnung der Mantisse
Da es sich um eine normalisierte Zahl handelt, wissen wir, dass sie eine 1 vor dem Komma hat: $1{,}00100110011001100110011$
Nun muss das Komma um 4 Stellen nach rechts verschoben werden: $10010{,}0110011001100110011$
Umwandlung in eine Dezimalzahl
Vorkommastellen: $10010_{2}=18_{10}$
Nachkommastellen: $0{,}0110011001100110011_{2}\approx 0.39999961853_{10}$
Um den Wert der Nachkommazahl zu erhalten, muss man denselben Prozess durchführen wie bei ganzen Zahlen, nur in umgekehrter Richtung, also von links nach rechts. Dabei muss der Exponent negativ sein und mit einer 1 beginnen.
${\begin{aligned}0\cdot 2^{-1}\\+1\cdot 2^{-2}\\+1\cdot 2^{-3}\\+0\cdot 2^{-4}\\+0\cdot 2^{-5}\\+1\cdot 2^{-6}\\\ldots \end{aligned}}$
Vorzeichen bestimmen
Das Vorzeichenbit ist eine Null, also handelt es sich um eine positive Zahl.
Komponenten zu einer Dezimalzahl zusammensetzen
$18{,}39999961853$

Interpretation des Zahlenformats

Die Interpretation hängt von dem Exponenten ab. Zur Erläuterung wird mit S der Wert des Vorzeichenbits (0 oder 1), mit E der Wert des Exponenten als nichtnegative ganze Zahl zwischen 0 und E_max = 11…111 = 2^r−1, mit M der Wert der Mantisse als nichtnegative Zahl und mit B der Biaswert bezeichnet. Die Zahlen r und p bezeichnen die Anzahl der Exponentenbits und Mantissenbits.

Charakteristik	Mantisse M	Bedeutung	Salopp	Bezeichnung
E = 0	M = 0	(−1)^S × 0	±0	Null (gehört zu denorm.)
E = 0	M > 0	(−1)^S × M / 2^p × 2^1−B	±0,M × 2^1−B	denormalisierte Zahl
0 < E < 2^r−1	M >= 0	(−1)^S × (1+M / 2^p) × 2^E−B	±1,M × 2^E−B	normalisierte Zahl
E = 2^r−1	M = 0	Unendlich	±∞	Unendlich
E = 2^r−1	M > 0	keine Zahl		keine Zahl (NaN)

Null

Null repräsentiert die vorzeichenbehaftete Null. Auch Zahlen, die zu klein sind, um dargestellt zu werden (Unterlauf), werden auf Null gerundet. Ihr Vorzeichen bleibt dabei erhalten. Negative kleine Zahlen werden so zu −0,0 gerundet, positive Zahlen zu +0,0. Beim direkten Vergleich werden jedoch +0,0 und −0,0 als gleich angesehen.

Normalisierte Zahl

Die Mantisse besteht aus den ersten n wesentlichen Ziffern der Binärdarstellung der noch nicht normalisierten Zahl. Die erste wesentliche Ziffer ist die höchstwertige (d. h. am weitesten links stehende) Ziffer, die von 0 verschieden ist. Da eine von 0 verschiedene Ziffer im Binärsystem nur eine 1 sein kann, muss diese erste 1 nicht explizit abgespeichert werden; gemäß der Norm IEEE 754 werden nur die folgenden Ziffern gespeichert, die erste Ziffer ist eine implizite Ziffer oder ein implizites Bit (engl. hidden bit). Dadurch wird gewissermaßen 1 Bit Speicherplatz „gespart“.

Denormalisierte Zahl

Ist eine Zahl zu klein, um in normalisierter Form mit dem kleinsten von Null verschiedenen Exponenten gespeichert zu werden, so wird sie als „denormalisierte Zahl“ gespeichert.[3] Ihre Interpretation ist nicht mehr ±1,mantisse·2^exponent, sondern ±0,mantisse·2^de. Dabei ist de der Wert des kleinsten „normalen“ Exponenten. Damit lässt sich die Lücke zwischen der kleinsten normalisierten Zahl und Null füllen. Denormalisierte Zahlen haben jedoch eine geringere (relative) Genauigkeit als normalisierte Zahlen; die Anzahl der signifikanten Stellen in der Mantisse nimmt zur Null hin ab.

Ist das Ergebnis (oder Zwischenergebnis) einer Rechnung kleiner als die kleinste darstellbare Zahl der verwendeten endlichen Arithmetik, so wird es im Allgemeinen auf Null gerundet; das nennt man Unterlauf der Gleitkommaarithmetik, engl. underflow. Da dabei Information verloren geht, versucht man, Unterlauf nach Möglichkeit zu vermeiden. Die denormalisierten Zahlen in IEEE 754 bewirken einen allmählichen Unterlauf (engl. gradual underflow), indem „um die 0 herum“ 2²⁴ (für single) bzw. 2⁵³ (für double) Werte eingefügt werden, die alle denselben absoluten Abstand voneinander haben und ohne diese denormalisierten Werte nicht darstellbar wären, sondern zu Unterlauf führen müssten.

Prozessorseitig sind denormalisierte Zahlen aufgrund ihres proportional seltenen Auftretens mit wenig Priorität implementiert und führen deswegen zu einer deutlichen Verlangsamung der Ausführung, sobald sie als Operand oder als Ergebnis einer Berechnung auftauchen. Um Abhilfe (z. B. für Computerspiele) zu schaffen, bietet Intel seit SSE2 die nicht IEEE-754-konforme Funktionalität an, denormalisierte Zahlen vollständig zu deaktivieren (MXCSR-Optionen „flush to zero“ und „denormals are zero“). Gleitkommazahlen, die in diesen Bereich gelangen, werden auf 0 gerundet.[4]

Unendlich

Der Gleitkommawert Unendlich repräsentiert Zahlen, deren Betrag zu groß ist, um dargestellt zu werden. Es wird zwischen positiver Unendlichkeit und negativer Unendlichkeit unterschieden. Die Berechnung von 1,0/0,0 ergibt nach Definition von IEEE-754 „positiv Unendlich“.

Keine Zahl (NaN)

Damit werden ungültige (oder nicht definierte) Ergebnisse dargestellt, z. B. wenn versucht wurde, die Quadratwurzel aus einer negativen Zahl zu berechnen. Einige „unbestimmte Ausdrücke“ haben als Ergebnis „keine Zahl“, zum Beispiel 0,0/0,0 oder „Unendlich“ – „Unendlich“. Außerdem werden NaNs in verschiedenen Anwendungsbereichen benutzt, um „Kein Wert“ oder „Unbekannter Wert“ darzustellen. Insbesondere der Wert mit dem Bitmuster 111…111 wird oft für eine „nicht initialisierte Gleitkommazahl“ benutzt.

IEEE 754 fordert zwei Arten von Nichtzahlen: stille NaN (NaNq – quiet) und signalisierende NaN (NaNs – signalling). Beide stellen explizit keine Zahlen dar. Eine signalisierende NaN löst im Gegensatz zu einer stillen NaN eine Ausnahme (Trap) aus, wenn sie als Operand einer arithmetischen Operation auftritt.

IEEE 754 ermöglicht dem Anwender das Deaktivieren dieser Traps. In diesem Falle werden signalisierende NaN wie stille NaN behandelt.

Signalisierende NaN können genutzt werden, um uninitialisierten Rechnerspeicher zu füllen, so dass jedes Verwenden einer uninitialisierten Variable automatisch eine Ausnahme auslöst.

Stille NaN ermöglichen den Umgang mit Rechnungen, die kein Ergebnis erzeugen können, etwa weil sie für die angegebenen Operanden nicht definiert sind. Beispiele sind die Division Null durch Null oder der Logarithmus aus einer negativen Zahl.

Stille und Signalisierende NaN unterscheiden sich im höchsten Mantissenbit. Bei stillen NaN ist dieses 1, bei signalisierenden NaN 0. Die übrigen Mantissenbits können zusätzliche Informationen enthalten, z. B. die Ursache der NaN. Dies kann bei der Ausnahmebehandlung hilfreich sein. Allerdings schreibt der Standard nicht fest, welche Informationen in den übrigen Mantissenbits enthalten sind. Die Auswertung dieser Bits ist daher plattformabhängig.

Das Vorzeichenbit hat bei NaN keine Bedeutung. Es ist nicht spezifiziert, welchen Wert das Vorzeichenbit bei zurückgegebenen NaN besitzt.

Rundungen

IEEE 754 unterscheidet zunächst zwischen binären Rundungen und binär-dezimalen Rundungen, bei denen geringere Qualitätsforderungen gelten.

Bei binären Rundungen muss zur nächstgelegenen darstellbaren Zahl gerundet werden. Wenn diese nicht eindeutig definiert ist (genau in der Mitte zwischen zwei darstellbaren Zahlen), wird so gerundet, dass das niederwertigste Bit der Mantisse 0 wird. Statistisch wird dabei in 50 % der Fälle auf-, in den anderen 50 % der Fälle abgerundet, so dass die von Knuth beschriebene statistische Drift in längeren Rechnungen vermieden wird.

Eine zu IEEE 754 konforme Implementierung muss drei weitere vom Programmierer einstellbare Rundungen bereitstellen: Rundung gegen +Unendlich (immer aufrunden), Rundung gegen −Unendlich (immer abrunden) und Rundung gegen 0 (Ergebnis immer betragsmäßig verkleinern).

Operationen

Zu IEEE 754 konforme Implementierungen müssen Operationen für Arithmetik, Berechnung der Quadratwurzel, Konversionen und Vergleiche bereitstellen. Eine weitere Gruppe von Operationen wird im Anhang empfohlen, jedoch nicht verbindlich vorgeschrieben.

Arithmetik und Quadratwurzel

IEEE 754 verlangt von einer (Hardware- oder Software-)Implementierung exakt gerundete Ergebnisse für die Operationen Addition, Subtraktion, Multiplikation und Division zweier Operanden sowie der Operation Quadratwurzel eines Operanden. Das heißt, das ermittelte Ergebnis muss gleich demjenigen sein, das bei einer exakten Ausführung der entsprechenden Operation mit anschließender Rundung entsteht.

Weiter ist die Berechnung des Restes nach einer Division mit ganzzahligem Ergebnis gefordert. Diese Restberechnung ist definiert durch $r=x-y\cdot n$ , $n$ ganzzahlig, $|n-{\tfrac {x}{y}}|<{\tfrac {1}{2}}$ oder bei geradem $n$ auch $|n-{\tfrac {x}{y}}|={\tfrac {1}{2}}$ . Dieser Rest muss ohne Rundung exakt ermittelt werden.

Konversionen

Konversionen werden zwischen allen unterstützten Gleitkommaformaten gefordert. Bei einer Konversion in ein Gleitkommaformat mit kleinerer Genauigkeit muss wie schon unter Arithmetik beschrieben exakt gerundet werden.

Zu IEEE 754 konforme Implementierungen müssen Konversionen zwischen allen unterstützten Gleitkommaformaten und allen unterstützten ganzzahligen Formaten bereitstellen. Die ganzzahligen Formate werden in IEEE 754 jedoch nicht genauer definiert.

Zu jedem unterstützten Gleitkommaformat muss eine Operation existieren, die diese Gleitkommazahl in die exakt gerundete ganze Zahl im selben Gleitkommaformat konvertiert.

Schließlich müssen Konversionen zwischen dem binären Gleitkommaformat und einem Dezimalformat existieren, die genau beschriebenen Mindestqualitätsforderungen genügen.

Vergleiche

Gleitkommazahlen nach IEEE 754 müssen verglichen werden können. Die Norm definiert die notwendigen Vergleichsoperationen und für alle möglichen Sonderfälle (vor allem NaN, Unendlich und 0) die geforderten Ergebnisse. Gegenüber den „schulmathematischen“ Vergleichen (kleiner, gleich oder größer) kommt als mögliches Ergebnis nach IEEE 754 vor allem unordered („nicht eingeordnet“) hinzu, wenn einer der Vergleichsoperanden NaN ist. Zwei NaN sind prinzipiell verschieden, auch wenn ihre Bitmuster übereinstimmen.

Empfohlene Operationen

Im Anhang der Norm werden zehn weitere Operationen empfohlen. Da sie in einer Implementierung im Grunde sowieso benötigt werden, läuft diese Empfehlung letztlich darauf hinaus, die Operationen an den Programmierer weiterzugeben. Diese Operationen sind (in C-Schreibweise): copysign (x, y), invertsign (x), scalb (y, n), logb (x), nextafter (x, y), finite (x), isnan (x), x ≠ y, unordered (x, y), class (x). Die Details der Implementierung vor allem wieder bei den Sonderfällen NaN usw. sind ebenfalls vorgeschlagen.

Exceptions, Flags und Traps

Treten bei der Berechnung Ausnahmen (Exceptions) auf, werden Status-Flags gesetzt. Im Standard wird vorgeschrieben, dass der Benutzer diese Flags lesen und schreiben kann. Die Flags sind „sticky“: werden sie einmal gesetzt, bleiben sie so lange erhalten, bis sie explizit wieder zurückgesetzt werden. Das Überprüfen der Flags ist beispielsweise die einzige Möglichkeit, 1/0 (=Unendlich) von einem Überlauf zu unterscheiden.

Des Weiteren wird im Standard empfohlen, Trap Handler zu ermöglichen: Tritt eine Ausnahme auf, wird der Trap Handler aufgerufen, anstatt das Status-Flag zu setzen. Es liegt in der Verantwortung solcher Trap Handler, das entsprechende Status-Flag zu setzen oder zu löschen.

Ausnahmen werden im Standard in 5 Kategorien eingeteilt: Überlauf, Unterlauf, Division durch Null, ungültige Operation und Ungenau. Für jede Klasse steht ein Status-Flag zur Verfügung.

Geschichte

In den 1960er und frühen 1970er Jahren hatte jeder Prozessor sein eigenes Format für Gleitkommazahlen und seine eigene FPU oder Gleitkommasoftware, mit der das jeweilige Format verarbeitet wurde. Dasselbe Programm konnte auf verschiedenen Rechnern unterschiedliche Resultate liefern. Die Qualität der verschiedenen Gleitkommaarithmetiken war ebenfalls sehr unterschiedlich.

Intel plante um 1976 für seine Mikroprozessoren eine eigene FPU und wollte die bestmögliche Lösung für die zu implementierende Arithmetik. Unter der Federführung der IEEE begannen 1977 Treffen, um FPUs für Gleitkommaarithmetik für Mikroprozessoren zu normieren. Das zweite Treffen fand im November 1977 unter dem Vorsitz von Richard Delp in San Francisco statt. Einer der richtungsweisenden Teilnehmer war William Kahan.

Um 1980 wurde die Anzahl der Vorschläge für die Norm auf zwei reduziert: Der K-C-S-Vorschlag (nach seinen Autoren Kahan, Coonen und Stone, 1977) setzte sich letztlich gegen die Alternative von DEC (F-Format, D-Format und G-Format) durch. Ein bedeutender Meilenstein auf dem Weg zur Norm war die Diskussion über die Behandlung des Unterlaufs, der bis dahin von den meisten Programmierern vernachlässigt worden war.

Intel implementierte gleichzeitig mit der Entwicklung der Norm die Normvorschläge weitgehend in der Intel FPU 8087, die als Gleitkomma-Coprozessor zum 8088 Verwendung fand. Die erste Version der Norm wurde 1985 verabschiedet und 2008 erweitert.

Literatur

IEEE 754: reprinted in SIGPLAN Notices, Vol. 22, Nr. 2, Feb. 1987, S. 9–25
Jean-Michel Muller: Elementary functions – Algorithms and Implementation. 2. Auflage. Birkhäuser, Lyon 2006, ISBN 0-8176-4372-9.

Weblinks

Commons: IEEE 754 – Sammlung von Bildern, Videos und Audiodateien

IEEE 754-1985 (PDF, 89 KiB)
IEEE Std 754-2019 vom 22. Juli 2019
IEEE Std 754-2008. (PDF) (Nicht mehr online verfügbar.) Archiviert vom Original am 6. November 2016; abgerufen am 30. Mai 2017 (englisch). Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2
Online-Umrechner zwischen Binär- und Dezimaldarstellung von IEEE 754-Gleitkommazahlen
Zur Geschichte: An Interview with the Old Man of Floating-Point (Reminiscences elicited from William Kahan by Charles Severance)
William Kahan: Lecture Notes on the Status of IEEE Standard 754 for Binary Floating-Point-Arithmetic, 1996
David Goldberg: What Every Computer Scientist Should Know About Floating-Point Arithmetic

Einzelnachweise

IEEE Standard for Floating-Point Arithmetic. In: IEEE Std 754-2019 (Revision of IEEE 754-2008). Juli 2019, S. 1–84, doi:10.1109/IEEESTD.2019.8766229 (ieee.org [abgerufen am 5. Februar 2020]).
IEEE 754-2008: Standard for Floating-Point Arithmetic, IEEE Standards Association, 2008, doi:10.1109/IEEESTD.2008.4610935
David Goldberg: What Every Computer Scientist Should Know About Floating-Point Arithmetic. In: ACM Computing Surveys. 23, 1991, S. 5–48. doi:10.1145/103162.103163. Abgerufen am 2. September 2010.
Shawn Casey: x87 and SSE Floating Point Assists in IA-32: Flush-To-Zero (FTZ) and Denormals-Are-Zero (DAZ). 16. Oktober 2008. Abgerufen am 3. September 2010.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] IEEE Standard for Floating-Point Arithmetic. In: IEEE Std 754-2019 (Revision of IEEE 754-2008). Juli 2019, S. 1–84, doi:10.1109/IEEESTD.2019.8766229 (ieee.org [abgerufen am 5. Februar 2020]).

[ieee754-2008-2] IEEE 754-2008: Standard for Floating-Point Arithmetic, IEEE Standards Association, 2008, doi:10.1109/IEEESTD.2008.4610935

[goldberg-3] David Goldberg: What Every Computer Scientist Should Know About Floating-Point Arithmetic. In: ACM Computing Surveys. 23, 1991, S. 5–48. doi:10.1145/103162.103163. Abgerufen am 2. September 2010.

[4] Shawn Casey: x87 and SSE Floating Point Assists in IA-32: Flush-To-Zero (FTZ) and Denormals-Are-Zero (DAZ). 16. Oktober 2008. Abgerufen am 3. September 2010.