Jiu Zhang Suanshu
Die Jiǔ Zhāng Suànshù (chinesisch 九章算術 / 九章算术 – „Neun Kapitel der Rechenkunst“, auch: ‚Neun Bücher arithmetischer Technik‘) ist eines der ältesten erhaltenen chinesischen Mathematikbücher und gleichzeitig eines der bekanntesten und bedeutendsten der Sammlung Zehn Mathematische Klassiker (Suanjing shi shu). Das Buch zeigt wohl den Stand der chinesischen Mathematik des 1. Jahrhunderts n. Chr.; es wurde auch in benachbarten Ländern wie Korea, Japan und Vietnam benutzt.[1]
Inhalt
Das Buch ist eine Aufgabensammlung von 246 Problemen, die in neun Kapiteln entsprechend Anwendungsfeldern im Alltagsleben (wie Bautechnik, Steuern, Handel, Landvermessung, Geldverleihen) gruppiert sind. Es werden jeweils die Problemstellung, die Lösung und der Lösungsweg angegeben.[2]
- Kapitel 1: Fāng tián (方田, fangtian – „Quadratisches Feld“), mit 38 Aufgaben über Flächenmaße aus der Landvermessung
- Kapitel 2: Sù mĭ (粟米 – „Hirse und Reis“), mit 46 Problemen aus dem Umfeld des Handels (Warentausch und Geldwechsel). Geübt werden Verhältnisrechnungen und Bruchrechnungen.
- Kapitel 3: Shuāi fēn (衰分 – „Abnehmende Anteile“) mit 20 Aufgaben, wieder vom Typ der Verhältnisaufgaben
- Kapitel 4: Shăo guăng (少廣 / 少广 – „Fehlende Breite“). 24 Aufgaben über Division (formuliert als Aufgabe, die zweite Seitenlänge einer Fläche zu finden, wenn eine Seitenlänge und Flächenmaß gegeben sind), Ziehen von Quadrat- und Kubikwurzel. Im Kommentar von Liu Hui wird das Problem besprochen, das Volumen einer Kugel zu bestimmen, was aber offenbleibt.
- Kapitel 5: Shāng gōng (商功 – „Abschätzung der Arbeit“), 28 Aufgaben aus der Bautechnik (wie Kanal- und Deichbau) über das Volumen verschiedener Körper. Im Kommentar gibt Liu Hui das Volumen der Pyramide.
- Kapitel 6: Jūnshū (均輸 / 均输 – „Gerechte Verteilung von Gütern“), 28 fortgeschrittenere Verhältnisaufgaben zu gerechter Verteilung von Gütern, zum Beispiel Aufgaben zur Verteilung von Soldaten auf Garnisonen an den Grenzen, Teilen und Transport von Gütern.
- Kapitel 7: Yíng bùzú (盈不足 – „Überfluss und Mangel“), 20 Aufgaben über lineare Gleichungen, die in einem Versuch-und-Irrtum-Verfahren gelöst werden, die der Regula falsi entspricht, die in Europa erst im 13. Jahrhundert bekannt war.
- Kapitel 8: Fāngchéng (方程 / 方程 – „Rechteck-Anordnungen“). 18 Aufgaben über Systeme linearer Gleichungen, die mit Gauß-Elimination gelöst werden, die in Europa erst durch Carl Friedrich Gauß bekannt wurde.
- Kapitel 9: Gōugŭ (勾股, gōugŭ – „Rechtwinklige Dreiecke“). 24 Probleme über rechtwinklige Dreiecke. Hier findet sich der Satz des Pythagoras (bei den Chinesen Gōugŭ-Regel[3]).
Überlieferung
Die älteste, heute bekannte Ausgabe der ersten fünf Kapitel der Neun Kapitel geht zurück auf das 13. Jahrhundert n. Chr., die anderen bekannten Gesamtausgaben beruhen auf Rekonstruktionen des Textes am Ende des 18. Jahrhunderts, die aus Zitaten der Neun Kapitel in einer heute fast vollständig verloren gegangenen Enzyklopädie aus dem Anfang des 15. Jahrhunderts erstellt wurden.[4] 1983–1984 wurden Inschriften auf Bambusstreifen aus der Zeit von 187 bis 157 v. Chr. entdeckt, deren Text Suan Shu Shu dem elementaren Teil des heutigen Textes der Neun Kapitel sehr ähnlich ist.[5] Ebenso lassen sich durch im Text verwendete Maße sowie Bezeichnungen wie Orts- und Steuerangaben Teile der Neun Kapitel in die frühe Han-Dynastie (206 v. Chr. – 9 n. Chr.) datieren. Für diese Datierung sprechen auch sehr ähnliche Textfragmente auf Holzstreifen, die in den Jahren 1899 und 1930 gefunden wurden.[6] Im China dieser Zeit scheint man außerdem das Seleukidenreich (312–63 v. Chr.) gekannt zu haben und es gibt Ähnlichkeiten von bestimmten Problemstellungen der Neun Kapitel zu solchen der babylonischen Mathematik, daher könnten Teile der Neun Kapitel babylonisch beeinflusst worden sein.[7] Es gibt jedoch auch Textteile, z. B. die Kapitel 4 und 8, die keinen Anhaltspunkt für eine Datierung bieten.[8]
Von den vielen Kommentaren zu den Neun Kapiteln sind aus dem 1. Jahrtausend n. Chr. nur die von Liu Hui (3. Jahrhundert n. Chr.), Li Chunfeng (602–670 n. Chr.) und ein Fragment von Zu Xuan (6. Jahrhundert n. Chr.) erhalten.[9] Liu Hui schrieb in seinem Vorwort, dass der erste chinesische Kaiser Qin Shihuangdi (er regierte als Kaiser von 221 bis 210 v. Chr.) schriftliche Aufzeichnungen verbrennen ließ, wodurch altes Wissen zerstört worden sei. Später habe Zhang Cang, der Gouverneur von Peking (um 165–142 v. Chr.), mit Mitarbeitern eine neue, vollständige Wiedergabe angefertigt, dabei seien einige Teile auch aktualisiert worden. Außerdem soll Geng Shouchang, zweiter Minister für Landwirtschaft (um 75–49 v. Chr.), bestimmte Teile überarbeitet haben.[10]
Man nimmt heute an, dass das Werk seine heutige Form im 1. Jahrhundert n. Chr. erhielt und dass seitdem neue Kenntnisse nur noch in die Kommentare eingingen.[11] Die Neun Kapitel der Rechenkunst sind ein wichtiger Bestandteil der zuerst von Li Chunfeng 644–648 n. Chr. zusammengestellten und mit Kommentaren versehenen Sammlung der Zehn Mathematischen Klassiker.[12]
Interpretation vom Satz des Pythagoras in den Neun Kapiteln nach Chemla
Die folgenden Bilder geben ein Diagramm aus den Neun Kapiteln wieder und dessen Interpretation zum Beweis des Satzes des Pythagoras nach der kritischen Ausgabe von Karine Chemla.
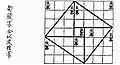Diagramm aus den Neun Kapiteln
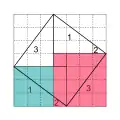Interpretation durch Chemla, Quadrate der Seitenlängen 3,4 über den Katheten zum Beispiel von Dreieck 1
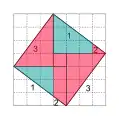Interpretation durch Chemla, Fortsetzung, Das große Quadrat, entsprechend dem Hypotenusenquadrat, hat denselben Flächeninhalt wie die Summe der Kathetenquadrate.
Ausgaben
Deutsche Ausgabe:
- Kurt Vogel: Neun Bücher Arithmetischer Technik. Vieweg 1968, ISBN 978-3-322-97959-9, doi:10.1007/978-3-322-98534-7
Englische Ausgaben:
- Kansheng Shen, u. a. (Hrsg.): The Nine Chapters on the Mathematical Art. Oxford University Press, Oxford 1999, ISBN 0-19-853936-3.
- Gekürzte Übersetzungen erschienen von:
- Florian Cajori: Arithmetic in Nine Sections. 1893.
- Lam Lay Yong: Jiu Zhang Suanshu, An Overview. Archive for History of Exact Science, Band 47, 1994, S. 1–51, doi:10.1007/BF01881700
Französisch/Chinesische Ausgabe, kritische Ausgabe:
- Karine Chemla, Shuchun Guo: Les neuf chapitres: le classique mathématique de la Chine ancienne et ses commentaires. Dunod, Paris 2004, ISBN 2-10-049589-5.
Literatur
- Karine Chemla: Jiuzhang Suanshu, in: Helaine Selin (Hrsg.): Encyclopaedia of the history of science, technology and medicine in non-western countries, Kluwer 2008
- Helmuth Gericke: Mathematik in Antike und Orient. Springer, Berlin u. a. 1984, S. 172–180.
- Jean-Claude Martzloff: A History of Chinese Mathematics. Springer, Berlin u. a. 1997, S. 127–136.
Anmerkungen
- Martzloff, S. 128.
- Martzloff, S. 131.
- Beim rechtwinkligen Dreieck heißt die kurze Kathete gōu („Grundseite“ oder „Fuß“) und die lange Kathete gŭ („Bein“).
- Martzloff, S. 128 f.
- Martzloff, S. 129.
- Martzloff, S. 130 f.
- Martzloff, S. 94–96.
- Martzloff, S. 131.
- Martzloff, S. 135.
- Martzloff, S. 129.
- Gericke, S. 173; Martzloff, S. 128.
- Martzloff, S. 123–126.