Maya-Kalender
Der Maya-Kalender ist als astronomischer Kalender das historische Kalendersystem der Maya. Es ist der am weitesten entwickelte Kalender der mesoamerikanischen Ureinwohner.
.jpg.webp)
Überblick
Die Maya nutzten für rituelle und zivile Zwecke verschiedene, einander ergänzende Kalender, die auf einer Tageszählung im Zwanzigersystem beruhen: den rituellen Tzolkin-Kalender, den zivilen Haab-Kalender und die Lange Zählung, mit der längere Zeiträume erfasst werden konnten, die für Himmelsbeobachtungen und historische Aufzeichnungen eine große Rolle spielten. Die Kombinationen von Tzolkin- und Haab-Daten wiederholen sich nach einer 52 Jahre dauernden Kalenderrunde.
Mit seinen 365 Tagen ähnelt der Haab zwar einem Sonnenkalender, ohne belegte Schalttage-Regelung kann man ihn allerdings nicht als solchen bezeichnen. Die 5 Extra-Tage des 19. Monats sind keine Schalttage, sondern haben den Charakter von Epagomenen. Ohne Bindung an die Mondphasen ist der Haab auch kein Lunarkalender. Der Tzolkin-Kalender ist – im Unterschied zu den meisten anderen historischen und modernen Kalendersystemen – nicht an den Sonnen- oder Mondrhythmus gebunden. Es gab zahlreiche Spekulationen, welchen astronomischen oder sonstigen Vorgaben dieses komplexe System folgt. Eine schlüssige Antwort steht noch aus und ist derzeit auch wegen der schlechten Quellenlage nicht zu erwarten.[1]
Die drei Bestandteile des Maya-Kalenders
Lange Zählung
Die Lange Zählung der Tage benötigten die Maya für astronomische Berechnungen und die Geschichtsaufzeichnung. Dabei laufen die einzelnen Stellen (wie 9.12.11.5.18) jeweils von [0..19], [0..19], [0..19], [0..17], [0..19], wobei das erste Baktun des Kalenders statt 0 Baktun einmalig abweichend 13 Baktun genannt wurde. Die lange Zählung stellt daher eine Datumsangabe dar, mit der jeder Tag seit dem Kalenderanfang am 11. August 3114 v. Chr. (13.0.0.0.0 4 Ahau 8 Cumku) eindeutig angegeben werden kann. Das älteste bisher gefundene Maya-Monument mit dem Datum 7 Baktun 16 Katun 3 Tun 2 Uinal 13 Kin lässt sich demnach auf den 5. Dezember 36 v. Chr. datieren.
Es fällt auf, dass der Beginn des Kalenders (13.0.0.0.0 4 Ahau 8 Cumku) und der Beginn des nächsten Baktun (13.0.0.0.0 4 Ahau 3 K'ank'in = 21. oder 23. Dezember 2012) den Datumsbestandteil 4 Ahau des Tzolkin-Kalenders enthalten. Das Tzolkin-Datum 4 Ahau bezieht sich nach der Mythologie der Maya auf die vier ersten Menschen bzw. Herren (Ahau) der gegenwärtigen Schöpfung, dem Menschen aus Mais.[2] Die Wiederholung dieses Datumsbestandteils nach 13 Baktun ist kein Zufall. Denn das kleinste gemeinsame Vielfache des 260-tägigen Tzolkin-Kalenders und eines 144.000 Tage dauernden Baktun ist nach 1.872.000 Tagen (= 13 Baktun) erreicht. Es lässt sich mathematisch zeigen, dass diese Eigenschaft auch für alle anderen Zeiteinheiten der Langen Zählung ab dem Uinal gilt.[3] Das bedeutsame Tzolkin-Datum 4 Ahau tritt also auch nach 13 Uinal, 13 Tun, 13 Katun, 13 Pictun, 13 Calabtun etc. wieder auf, wie sich leicht nachprüfen lässt. Darin soll dem Autor Marcel Polte zufolge zugleich die Antwort auf die bislang ungeklärte Frage liegen, warum die Maya bei der Langen Zählung als „Jahr“ bzw. Tun einen Zeitraum von 360 Tagen zugrunde legten, obwohl sie eine sehr genaue Kenntnis von der tatsächlichen Dauer des Sonnenjahres hatten und auch der Haab-Kalender 365 Tage umfasste. Durch die Verkürzung des „Jahres“ auf ein Tun mit 360 Tagen konnte sich das 4-Ahau-Datum nach 13 Tun-Zyklen wieder einstellen; für ein Tun mit 365 Tagen hätte dies nicht funktioniert.[4]
Zeiträume
Kin, Uinal, Tun, Katun, Baktun, Pictun, Calabtun, Kinchiltun und Alautun sind Bezeichnungen für Zeiträume in der Langen Zählung des Maya-Kalenders. Die Bezeichnungen höher als Baktun sind moderne Erfindungen von Forschern, die ursprünglichen Bezeichnungen sind nicht bekannt. Diese hohen Zahlenwerte kommen nur in einer kleinen Anzahl von Inschriften und im Dresdner Mayacodex vor.
| Stellenwertposition | Berechnung | Zahlenwert | Name | Logogramm(e) |
|---|---|---|---|---|
| 1 | 1 | 1 | k'in |  |
| 2 | 20 k'in | 20 | uinal |   |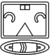
| 3 | 18 uinal | 360 | tun |    |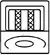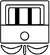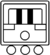
| 4 | 20 tun | 7.200 | k'atun |  |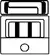
| 5 | 20 k'atun | 144.000 | baktun |   |
| 6 | 20 baktun | 2.880.000 | pictun | |
| 7 | 20 pictun | 57.600.000 | calabtun | |
| 8 | 20 calabtun | 1.152.000.000 | kinchiltun | |
| 9 | 20 kinchiltun | 23.040.000.000 | alautun |
Haab
Das Haab diente den Maya zu zivilen Zwecken, wie zur Berechnung der Saat- und Erntezeiten und ähnelt unserem Kalender, da es mit 365 Tagen rund ein Sonnenjahr umfasst. Im Haab-Kalender wird das Jahr in 18 „Monate“ mit je 20 Tagen und dem 19. „Monat“ mit 5 „Unglückstagen“ unterteilt. Nach Diego de Landa haben die Maya zusätzlich in jedem vierten Jahr einen Schalttag eingeschoben.[5] Jedoch macht de Landa keine Angaben darüber, wie dabei der parallele Lauf von Haab und Tzolkin erhalten blieb. Ob tatsächlich Schalttage verwendet wurden, ist mangels anderer Quellen deshalb nicht bekannt. Aus diesem Grund kann auch keine Aussage über den Jahresbeginn des Haab in vorspanischer Zeit gemacht werden.[6]
- Standard-Inskriptionsformen(?) bis auf Monat 4 u. 15
Monat 01:
Pop
Monat 02:
Uo
Monat 03:
Zip
Monat 04:
Zotz (Sotz')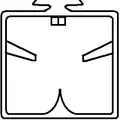
Monat 05:
Zec (Sek)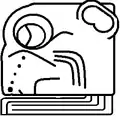
Monat 06:
Xul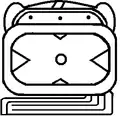
Monat 07:
Yaxkin (yaxk'in)
Monat 08:
Mol
Monat 09:
Chen (Ch'en)
Monat 10:
Yax
Monat 11:
Zac (Sak)
Monat 12:
Ceh
Monat 13:
Mac (Mak)
Monat 14:
Kankin
Monat 15:
Muan
Monat 16:
Pax
Monat 17:
Kayab
Monat 18:
Cumku
Monat 19:
Uayeb / Wayeb („Unglückstage“; Zusatzmonat mit nur 5 Epagomenen)
Tzolkin
Für rituelle Zwecke benutzten die Maya den Tzolkin („Zählung der Tage“), bei dem jeder Tag (Kin) durch eine Kombination einer Zahl (Ton) von 1 bis 13 mit dem Namen einer von 20 Schutzgottheiten (oder Tagesnamen) bezeichnet wird. Ein Tzolkin-Datum bezeichnet daher einen bestimmten Tag in einer Periode von 260 Tagen und wird beispielsweise als 6 Edznab angegeben.
Kalenderrunde
Da der Haab-Kalender 365 Tage und der Tzolkin-Kalender 260 Tage umfasst, wiederholen sich alle 18.980 Tage oder 52 Haab-Jahre bzw. 73 Tzolkin-Jahre die Kombinationen von Haab- und Tzolkin-Daten. Dieser Zeitraum wird als Kalenderrunde bezeichnet, innerhalb deren eine Kombination aus Haab- und Tzolkin-Datum eindeutig ist.
Vollständige Datumsangabe und Umrechnung
| Datumsteil | Berechnung mit Stellenwert | Zwischensumme [Tage] | |
|---|---|---|---|
| 9 | Baktun-Perioden | 9 × 144.000 | 1.296.000 |
| +12 | Katun-Perioden | 12 × 7.200 | 86.400 |
| +11 | Tun-Perioden | 11 × 360 | 3.960 |
| + 5 | Uinal-Perioden | 5 × 20 | 100 |
| +18 | Kin (Tage) | 18 × 1 | 18 |
| Summe der Datumsteile | 1.386.478 | ||
Der Todestag (31. August 683) des Herrschers Pakal I. von Palenque lautet im Maya-Kalender 9.12.11.5.18 6 Edznab 11 Yax:
- 9.12.11.5.18 gibt den Tag als Lange Zählung an
- 6 Edznab den Tag im Tzolkin-Kalender und
- 11 Yax ist der Tag im Haab-Kalender.
Das bedeutet: Pakal I. von Palenque starb 1.386.478 Tage nach Erschaffung der Welt (13. August 3114 v. Chr.).
Für die Umrechnung eines Datums des Maya-Kalenders in andere Kalendersysteme, insbesondere den europäischen julianischen oder gregorianischen Kalender, wird eine Korrelationszahl verwendet, die die Differenz zwischen dem Zahlenwert der Langen Zählung der Maya und dem julianischen Tag angibt. Trotz zahlreicher unterschiedlicher Ansätze wird die sogenannte Thompson-Gleichung von 584.284 ± 1 Tag von der Mehrzahl der Fachleute akzeptiert und angewandt.[7]
„Weltuntergangstag“
Besondere Aufmerksamkeit wurde in esoterischen Kreisen dem 21. bzw. 23. Dezember 2012 gewidmet. Man wollte hier einen angeblichen „Weltuntergangstag“ der Maya-Schöpfung erkennen. Nach Ansicht von Mayaforschern war dies inhaltlich völlig unzutreffend.[8] Korrekt ist, dass an diesem Tag in der Langen Zählung zum ersten Mal seit dem Jahre 3114 v. Chr. der Zahlenwert des Ausgangstages des aktuellen dreizehnten Baktun-Zyklus der Langen Zählung (13.0.0.0.0) wiederkehrte.[9] Dieser Zahlenwert tritt nach der Schematik des Maya-Kalenders regelmäßig nach 1.872.000 Tagen (ca. 5128 Jahren) ein. Die Datumsangaben der Langen Zählung unterscheiden sich jedoch beim Wiederkehren durch eine unterschiedliche Position im Haab-Jahr. So fällt das Datum 13.0.0.0.0 im Jahre 3114 v. Chr. auf den Tag 8 Cumku, im Jahre 2012 auf den Tag 3 Kankin, danach auf 18 Ch'en usw. Die Maya haben nachweislich über den Endtag des Baktun-Zyklus sowohl weit in die Vergangenheit wie in die Zukunft gerechnet und mit diesen Daten mythisch-dynastische Ereignisse verbunden.[10] So wird ein Thronjubiläum des Herrschers Pakal im Jahr 4772 genannt.[11]
Das Datum 13.0.0.0.0 4 Ahau 8 Cumku wurde von den Maya als Tag der Schöpfung der Welt in ihrer gegenwärtigen Form angesehen.[12] Allerdings wurden bisher auch keine Inschriften entdeckt, die auf den Beginn einer neuen Schöpfung am Tage 13.0.0.0.0 4 Ahau 3 Kankin im Jahr 2012 hindeuten würden. Lediglich das Inschriftenmonument 6 aus dem (nicht mehr vorhandenen) Fundort El Tortuguero westlich von Palenque bezieht sich auf dieses Datum und spricht etwas kryptisch davon, dass an diesem Tag die Gottheit Bolon Yokte' K'uh in einem großen Akt der Bekleidung und Vorstellung (eines Amtsträgers) auftreten wird.[13]
In einer Publikation der Science wird vom Fund eines Kalenders aus dem 9. Jahrhundert in den Ruinen der Maya-Hochburg Xultun im heutigen Guatemala berichtet.[14] US-Forscher haben dort Wandmalereien aus dem 9. Jahrhundert entdeckt, die neben menschlichen Figuren die bislang ältesten astronomischen Kalender der Maya zeigen. Der Studienleiter William A. Saturno meint: „Die alten Maya sagten voraus, dass die Welt weitergehen würde und dass die Dinge in 7000 Jahren genauso sein würden wie heute“.[15][16]
Siehe auch
- Liste der Kalendersysteme
- Maya-Codices, genauer Codex Dresdensis – Quelle für Entdeckung des Maya-Kalendersystems
Literatur
- Linda Schele, David Freidel: Die unbekannte Welt der Maya. Albrecht Knaus, München 1991, ISBN 3-8135-6342-1.
- Hugo Stamm: Im Bann des Maya-Kalenders – Endzeithysterie in Sekten und Esoterik. Gütersloher Verlagshaus, 2012, ISBN 978-3-579-06674-5.
Weblinks
- Codex Dresdensis - Mscr.Dresd.R.310 Dresdner Mayahandschrift der Sächsischen Landesbibliothek – Staats- und Universitätsbibliothek Dresden online
- Der Maya-Kalender
Einzelnachweise
- Herbert Metz: Die Grundlagen des julianischen und gregorianischen Kalenders. In: computus.de. 2002, abgerufen am 24. Februar 2010.
- Jens Rohark, Mario Krygier: Don Eric und die Maya. 23. Dezember 2012. Werden die Götter wiederkommen? docupoint, Magdeburg 2006, S. 145
- Marcel Polte: 2012. Countdown der Apokalypse? - Eine Spurensuche. Books on Demand, Norderstedt 2010, S. 58 f.
- Marcel Polte: 2012. Countdown der Apokalypse? - Eine Spurensuche. Books on Demand, Norderstedt 2010, S. 59 f.
- Diego de Landa: Bericht aus Yucatán, Reclam, Stuttgart S. 100.
- Nikolai Grube (Hrsg.): Maya. Tandem Verlag, China 2007/2007, S. 135
- Hanns J. Prem: Manual de la antigua chronología mexicana. CIESAS, México 2008, ISBN 978-968-496-694-9.
- Linda Schele, David Freidel: Die unbekannte Welt der Maya. Albrecht Knaus, München 1991, S. 74.
- Linda Schele, David Freidel: Die unbekannte Welt der Maya. Albrecht Knaus, München 1991, S. 511 f.
- Elisabeth Wagner, in Nicolai Grube (Hrsg.): Maya. Gottkönige im Regenwald. h.f.ullmann, 2007, S. 283.
- Bernd Ingmar Gutberlet: Der Maya-Kalender. Ehrenwirth, Bergisch Gladbach 2009, S. 240.
- Elisabeth Wagner, in Nicolai Grube (Hrsg.): Maya. Gottkönige im Regenwald. h.f.ullmann, 2007, S. 281.
- Sven Gronemeyer, Barbara MacLeod: What Could Happen in 2012: A Re-Analysis of the 13-Bak'tun Prophecy on Tortuguero Monument 6 (PDF; 9,9 MB). In: Wayeb Notes. Nr. 34, 2010, S. 4 ff.
- William A. Saturno, David Stuart, Anthony F. Aveni, Franco Rossi: Ancient Maya Astronomical Tables from Xultun, Guatemala. In: Science. Bd. 336, 11. Mai 2012, S. 714–717.
- Kein Weltuntergang für die Maya. Auf: wissenschaft.de vom 10. Mai 2012. Abgerufen am 10. September 2019.
- Dagmar Röhrlich: Alte Zeitrechnung: Bislang ältester astronomischer Kalender der Maya entdeckt. In: Deutschlandfunk, 11. Mai 2012. Abgerufen am 30. Juli 2012.