Integer (Datentyp)
Mit Integer ([ˈɪnteɡɐ], englisch [ˈɪntɪdʒə], für ganze Zahl; von lateinisch numerus integer) wird in der Informatik ein Datentyp bezeichnet, der ganzzahlige Werte speichert. Der Wertebereich ist endlich. Berechnungen mit Integern sind in der Regel exakt. Lediglich ein Überlauf kann durch Überschreiten des zulässigen Wertebereichs auftreten. Als grundlegender arithmetischer Datentyp sind Integer in der Hardware fast aller Rechenanlagen vorhanden und in nahezu jeder Programmiersprache verfügbar. Meist werden sogar mehrere Integerarten bereitgestellt, die sich in der Darstellung, der Länge oder dem Vorhandensein eines Vorzeichens unterscheiden. Die implementierte Arithmetik mit Integern ist bisher nicht genormt und weist oft sprachabhängige (Java, C) oder sogar compilerabhängige (C – Reihenfolge der Auswertung von Ausdrücken) Eigenheiten auf. Ein Normungsversuch liegt mit der „Language Independent Arithmetic“ (ISO/IEC 10967)[1] vor.
Darstellungen
Von exotischen Darstellungen[2] abgesehen, gibt es drei Möglichkeiten zur Speicherung von Integer-Variablen. Das Vorzeichen – soweit vorhanden – kann man in allen Darstellungen an einer bestimmten Ziffer ablesen.
In der Betrags-Vorzeichendarstellung werden das Vorzeichen und der Betrag getrennt gespeichert und verarbeitet.
Bei b-Komplementzahlen (Zweierkomplementzahlen) wird genau die halbe Teilmenge der Zahlen mit großem Betrag als negative Zahlen interpretiert, ohne dass die Arithmetik positiver Zahlen wesentlich geändert wird. Das führt zu einfachen Schaltungen und zu einer einfachen Regel für Vorzeichenänderungen (ziffernweises b-Komplement und anschließende Erhöhung der Zahl). Zwischen der Arithmetik mit Zweierkomplementzahlen und rein positiven Binärzahlen besteht kein Unterschied. Es existiert eine bijektive Abbildung zwischen den Darstellungen und den Werten (kein Wert hat zwei Darstellungen). Man kann b-Komplementzahlen wie technische Zähler (Kilometerzähler im Auto) interpretieren. Nachteil von b-Komplementzahlen ist, dass der kleinste negative Wert kein positives Gegenstück in der Darstellung hat.
Bei (b−1)-Komplementzahlen (Einerkomplementzahlen) vereinfacht man dagegen die Regel für Vorzeichenänderungen (die anschließende Erhöhung fällt weg) und muss dafür in der Arithmetik mehr Fallunterscheidungen und vor allem zwei Darstellungen der Null (±0) berücksichtigen.
In modernen Rechenanlagen ist die Basis b praktisch ausnahmslos b = 2 und die Darstellung im Zweierkomplement hat sich weitgehend durchgesetzt.
Dezimale Äquivalente zum Zweier- und Einerkomplement im Binärsystem wären Zehner- und Neunerkomplementzahlen.
Von manchen Herstellern wird oft unter Berufung auf Kundenwünsche (Banken) noch ein Dezimalformat gepflegt. Hier wird fast ausnahmslos eine Betrags-Vorzeichendarstellung gewählt und der Betrag in der sogenannten BCD-Form (binary coded decimal) gespeichert. Der Wunsch ist begründet, da bei der Umwandelung einer Dezimalzahl in eine Integerzahl oder zurück Rundungsfehler auftreten, die eine exakte kaufmännische Buchhaltung unmöglich macht.
Übersicht
| Zweierkomplement | Einerkomplement | Betrags-Vorzeichendarstellung | BCD-Zahlen | |
|---|---|---|---|---|
| Basis | 2 | 2 | 2 | 10 |
| Eindeutigkeit | umkehrbar eindeutig | 2 Darstellungen für den gleichen Wert (±0) | 2 Darstellungen für den gleichen Wert (±0) | Darstellungen ohne Wert |
| Wertebereich | maximal, asymmetrisch | symmetrisch | symmetrisch | symmetrisch |
Beispiele
(die Beispielzahlen sind für 9 Bit ausgelegt, da so zweistellige BCD-Zahlen möglich sind, Darstellung MSB → LSB):
| Zweierkomplement | Einerkomplement | Betrags-Vorzeichendarstellung | BCD-Zahlen | |
|---|---|---|---|---|
| Maximum | 0 1111 1111 (255) | 0 1111 1111 (255) | 0 1111 1111 (255) | 0 1001 1001 (99) |
| 17 | 0 0001 0001 | 0 0001 0001 | 0 0001 0001 | 0 0001 0111 |
| 5 | 0 0000 0101 | 0 0000 0101 | 0 0000 0101 | 0 0000 0101 |
| 1 | 0 0000 0001 | 0 0000 0001 | 0 0000 0001 | 0 0000 0001 |
| 0 | 0 0000 0000 | 0 0000 0000 | 0 0000 0000 | 0 0000 0000 |
| −0 | 1 1111 1111 | 1 0000 0000 | 1 0000 0000 | |
| −1 | 1 1111 1111 | 1 1111 1110 | 1 0000 0001 | 1 0000 0001 |
| −2 | 1 1111 1110 | 1 1111 1101 | 1 0000 0010 | 1 0000 0010 |
| −5 | 1 1111 1011 | 1 1111 1010 | 1 0000 0101 | 1 0000 0101 |
| −17 | 1 1110 1111 | 1 1110 1110 | 1 0001 0001 | 1 0001 0111 |
| Minimum+1 | 1 0000 0001 (−255) | 1 0000 0001 (−254) | 1 1111 1110 (−254) | 1 1001 1000 (−98) |
| Minimum | 1 0000 0000 (−256) | 1 0000 0000 (−255) | 1 1111 1111 (−255) | 1 1001 1001 (−99) |
Häufige Speicherformen
Ein Integer besteht in der Regel aus 8, 16, 32, 64 oder 128 Bits (also 1, 2, 4, 8 oder 16 Bytes) – entsprechend der Wortbreite der jeweiligen CPU. Historisch wurden auch andere Werte (12, 48, … Bit) verwendet. In Programmiersprachen sind die Bezeichnungen dieser Zahlen teilweise genormt: In Java werden sie als byte (8), short (16), int (32) und long (64 Bit) bezeichnet. In C gibt es dieselben Bezeichner für Typen, die jedoch in ihrer Größe architekturabhängig variieren. Dafür unterstützt C vorzeichenlose (unsigned) Integer-Varianten, mit denen viele ältere und auch solche Prozessoren ausschließlich oder vorrangig (unmittelbar) arbeiten, wie sie heute noch in Mikrocontrollern und eingebetteten Systemen Anwendung finden. Erst mit C99 wurden plattformunabhängige Typen spezifiziert, die gemäß ihrer expliziten Wortbreite in Bits eindeutig definiert sind, so z. B. für die ein Byte breiten: int8_t resp. uint8_t.
Rechenanlagen verarbeiten Integer meist schneller als Gleitkommazahlen, da oft weniger Bits zu verarbeiten sind (die kleinste IEEE-754-Gleitkommazahl hat 32 Bit) und die Verarbeitung des Exponenten entfällt, was Rechenzeit und Speicherplatz einspart. Zusätzlich bietet eine reine Festkommaarithmetik (Integer basierend) gegenüber Gleitkommaarithmetik den Vorteil der exakten Verarbeitung (innerhalb fester Dynamikgrenzen), datenabhängige Effekte wie Denormalisierung oder Absorption treten nicht auf.[3] Für interne Software von Geldinstituten wird deswegen häufig reine Integerverarbeitung gefordert, wie es z. B. bei GnuCash realisiert ist.[4] Andere Softwarelösungen, beispielsweise das ERP-System SAP S/4HANA verwenden jedoch BCD-kodierte Festkommazahlen.
Bei der Ablage im Speicher taucht neben der Notwendigkeit, die Bits der Zahlendarstellung überhaupt abzulegen, noch das Problem der Bytereihenfolge und Anordnung auf.
Maximaler Wertebereich
| Größe (Bit) |
Typische Namen | Vorzeichen | Grenzen des Wertebereichs (Zweierkomplement) | Dezimalstellen (ohne Vorzeichen) | |
|---|---|---|---|---|---|
| min | max | ||||
| 8 | char, Byte/byte, modern: int8_t bzw. uint8_t | signed | −128 | 127 | 3 |
| unsigned | 0 | 255 | 3 | ||
| 16 | Word, Short/short, Integer, modern: int16_t bzw. uint16_t | signed | −32.768 | 32.767 | 5 |
| unsigned | 0 | 65.535 | 5 | ||
| 32 | DWord/Double Word, int, long (Windows auf 16/32/64-Bit Systemen;[5] Unix/Linux/C99 auf 16/32-Bit Systemen[5]), modern: int32_t bzw. uint32_t | signed | −2.147.483.648 | 2.147.483.647 | 10 |
| unsigned | 0 | 4.294.967.295 | 10 | ||
| 64 | Int64, QWord/Quadword, long long, Long/long (Unix/Linux/C99 auf 64-Bit Systemen[5][6][7]), modern: int64_t bzw. uint64_t | signed | −9.223.372.036.854.775.808 | 9.223.372.036.854.775.807 | 19 |
| unsigned | 0 | 18.446.744.073.709.551.615 | 20 | ||
| 128 | Int128, Octaword, Double Quadword | signed | ≈ −1,70141·1038 | ≈ 1,70141·1038 | 39 |
| unsigned | 0 | ≈ 3,40282·1038 | 39 | ||
| n | BigInteger | signed | −2n−1 | 2n−1 − 1 | ⌈log10 2n−1⌉ |
| unsigned | 0 | 2n − 1 | ⌈log10 2n⌉ | ||
Arithmetischer Überlauf

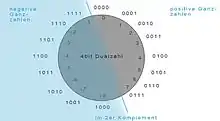
Wird einer Integer-Variable ein Wert außerhalb ihres Wertebereiches zugewiesen, führt dies zu einem arithmetischen Überlauf. So wird z. B. bei einer vorzeichenlosen 8-Bit-Integer-Variablen aus 255+1 der Wert 0; bei einer vorzeichenbehafteten im Zweierkomplement hingegen aus 127+1 der Wert −128.
Siehe auch
Literatur
- Donald E. Knuth: The Art of Computer Programming. 2. Seminumerical Algorithms. 3. Auflage. Addison-Wesley, 1997, ISBN 0-201-89684-2.
Einzelnachweise und Anmerkungen
- ISO/IEC 10967 in der englischsprachigen Wikipedia
- Knuth: Band 2. S. 195, 4.1 Positional number systems; S. 284, 4.3.2 Modular arithmetic
- David Goldberg: What Every Computer Scientist Should Know About Floating-Point Arithmetic. In: ACM Computing Surveys. 23, 1991, S. 5–48. doi:10.1145/103162.103163. Abgerufen am 2. September 2010.
- What’s new in GnuCash 1.6?. gnucash.org. Abgerufen am 3. September 2010.
- Agner Fog: Calling conventions for different C++ compilers and operating systems: Chapter 3, Data Representation (PDF; 416 kB) 16. Februar 2010. Abgerufen am 30. August 2010.
- Eric Giguere: The ANSI Standard: A Summary for the C Programmer. 18. Dezember 1987. Abgerufen am 4. September 2010.
- Randy Meyers: The New C: Integers in C99, Part 1. drdobbs.com. 1. Dezember 2000. Abgerufen am 4. September 2010.