Netzwerkinferenz (Systembiologie)

Netzwerkinferenz (Rekonstruktion von Netzwerken, Inferenz (aus lateinisch inferre): Schlussfolgerung) bezeichnet die Identifikation oder Rekonstruktion eines Netzwerkmodells eines realen Systems unter Verwendung von Messdaten und Vorwissen. In der Systembiologie bezeichnet Netzwerkinferenz die Identifikation von biologischen Netzwerken, insbesondere Genregulationsnetzwerken, unter Verwendung sowohl von gemessenen biomedizinischen oder/und molekularbiologischen Daten, insbesondere Daten aus der Genexpressionsanalyse, als auch von molekularbiologischem Vorwissen. In der Geräte- und Software-Technik wird die Netzwerkinferenz Reverse Engineering genannt; dieser Begriff wird im übertragenen Sinne auch für die Netzwerkinferenz in der Systembiologie verwendet.

Biologisches Netzwerk

Die Eigenschaften und das Verhalten vieler Systeme können durch Netzwerkmodelle abgebildet und simuliert werden. Ein Netzwerk besteht aus Komponenten (Knoten), die über Kanten miteinander verbunden sind. In der Systembiologie repräsentieren Knoten insbesondere Gene, Proteine, Metabolite, Zellen, Gewebe, Organe, Organismen oder Arten. Die Kanten repräsentieren molekularbiologische und biochemische Prozesse (z. B. Transkription, Translation, enzymatisch katalysierte Reaktionen), Interaktionen (z. B. Protein-Protein-Interaktionen), metabolische Vorgänge, Informationsflüsse oder trophische Beziehungen in Nahrungsketten. Beispielsweise besteht ein Genregulationsnetzwerk (GRN) aus Knoten, die die Gene repräsentieren, und aus Kanten, die die Gene verbinden. Die Verbindungen repräsentieren vereinfachend die Prozesse der Genexpression über die Synthese bestimmter Proteine mit genregulatorischer oder katalytischer Funktion (Transkriptionsfaktoren, Repressoren, Induktoren oder Enzyme, die über biochemische Reaktionen die Synthese von Metaboliten katalysieren, die auf die Signaltransduktion einwirken und so die Expression von Genen beeinflussen).

Netzwerkinferenz als Lösung eines Optimierungsproblems

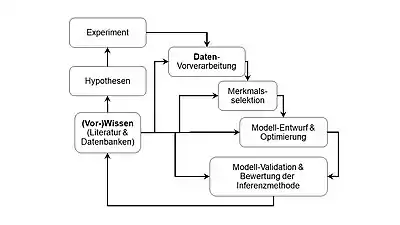
Zyklische Inferenz von Netzwerkmodellen

Netzwerkinferenz wird als die Lösung eines Optimierungsproblems verstanden, bei dem die Eigenschaften des Netzwerkmodells mit den gemessenen Daten unter bestimmten Randbedingungen in möglichst große Übereinstimmung (Ähnlichkeit) gebracht werden. Zur Quantifizierung der Übereinstimmung gibt es verschiedene Maße für den Abstand zwischen den Messdaten einerseits und den Werten andererseits, die im Ergebnis der Simulation des Netzwerkmodells erhalten werden. Bei dynamischen Systemen, wie einem GRN, wird die Antwort des biologischen Systems (z. B. eines Organs oder Organismus) auf eine äußere Störung (z. B. Temperatursprung, Infektion, Gabe eines Wirkstoffs) gemessen und mit der simulierten Antwort des GRN verglichen, d. h. der Abstand von Messung und Berechnung bestimmt. Wenn anstelle nur eines Störimpulses die Antworten auf mehrere verschiedene Störungen in die Netzwerkinferenz einbezogen werden, können komplexere Netzwerke identifiziert werden.[1]

Die Randbedingungen für das Optimierungsproblem werden u. a. durch das vorhandene Vorwissen über das Netzwerk bestimmt. Wenn das Vorwissen mit Ungewissheiten behaftet ist oder seinerseits eine Optimierungsaufgabe impliziert (z. B. „Die Zahl der aktiven Kanten soll möglichst klein sein“), kann das Vorwissen auch in die Formulierung der Zielfunktion (Bewertungsfunktion) neben der Minimierung des Abstands zwischen Netzwerkmodell- und Systemverhalten (z. B. additiv) aufgenommen werden.

Die verschiedenen Algorithmen der Netzwerkinferenz unterscheiden sich hinsichtlich[2]

der Verwendung und Vorverarbeitung von Messdaten,
des Netzwerktyps und der Methodik der Modellsimulation,
der Art und Weise der Reduktion der Komplexität des Netzwerkmodells,
der Verwendung von Vorwissen und Hypothesen.

Messdaten

Die gemessenen Daten sollen das Systemverhalten mit einem möglichst hohen Informationsgehalt wiedergeben. Bei dynamischen Systemen, wie einem GRN, wird zu diesem Zweck die Antwort des (biologischen) Systems (z. B. eines Organs oder Organismus) auf eine äußere Störung gemessen und mit der simulierten Antwort des (GRN-)Modells verglichen, d. h. der Abstand beider Zeitreihen beispielsweise als Euklidischer Abstand oder mit der Manhattan-Metrik bestimmt. Die Art der Störung, ggf. die Anzahl der Versuchswiederholungen und auch die Anzahl und Allokation der Messungen (z. B. Messzeitpunkte) kann durch optimale statistische Versuchsplanung bestimmt werden. Die zu wählende Messmethodik ist vor allem durch das System und die verfügbaren Ressourcen bestimmt. Für die Inferenz von GRN stehen verschiedene Methoden der Genexpressionsanalyse, z. B. RNA-Seq, zur Verfügung.

Netzwerktypen

Ein Netzwerk ist ein Modell eines realen Systems. Netzwerke werden oft durch Graphen visualisiert und können mit Methoden der Graphentheorie analysiert werden, so dass auch metrische Eigenschaften der Graphen, beispielsweise die Cliquenzahl, in die Zielfunktion des o. g. Optimierungsproblems aufgenommen werden können.[3] Man unterscheidet bezüglich der Eigenschaft der Kanten gerichtete und ungerichtete Graphen, je nachdem, ob Verbindungen oder Zusammenhänge zwischen den Knoten (bevorzugte) Richtungen aufweisen. Und man unterscheidet gewichtete und ungewichtete Kanten, je nachdem, ob den Kanten Werte, z. B. reelle Zahlen für Reaktionsgeschwindigkeiten, zugeordnet werden. Verschiedene Netzwerktypen werden hinsichtlich der verschiedenen Möglichkeiten der mathematischen Darstellung der Knoten und Kanten unterschieden. Im einfachsten Fall kann das Netzwerk mit Methoden der Booleschen Algebra beschrieben werden. In einem solchen Booleschen Netzwerk repräsentiert beispielsweise Wert 1 ein exprimiertes Gen und Wert 0 ein nicht exprimiertes („schlafendes“) Gen. Eine Erweiterung führt dazu, dass anstelle der zweiwertigen Logik mit Wahrscheinlichkeiten gerechnet wird. Typischerweise wird damit ein Bayessches Netz formuliert, wobei die Knoten mit der Wahrscheinlichkeit, dass ein Gen exprimiert ist, bewertet werden und die Kanten von Gen A zu Gen B mit der bedingten Wahrscheinlichkeit, dass Gen B hochreguliert ist, falls A hochreguliert ist. Drittens kann die relative oder absolute Menge des Transkripts (Expressionsintensität), also die Menge der mRNA, im Ergebnis der Transkription eines Gens durch eine reelle Zahl quantifiziert werden.

Die einen Knoten repräsentierenden Werte (Boolesche Einheit, Wahrscheinlichkeit, reelle Zahl) können entweder konstant oder zeitlich variabel sein, so dass man zwischen statischen und dynamischen Netzwerken unterscheidet. Kanten eines Netzwerks werden häufig nicht nur durch Zahlen bewertet, sondern durch mathematische Funktionen unterschiedlicher Komplexität. Wenn in dynamischen Netzwerken die Knoten durch reelle Zahlen repräsentiert werden, werden vielfach für die mathematische Darstellung von Kanten (gewöhnliche) Differentialgleichungen oder Differenzengleichungen verwendet.

Reduktion der Komplexität

Die Komplexität eines Netzwerks hängt vom Netzwerktyp, der Anzahl der Knoten und Kanten sowie der mathematischen Funktion, mit der die Kanten bewertet werden, ab. Biologische Systeme sind mit ihren Tausenden von Genen, Proteinen, Metaboliten, Zellen usw. hochdimensional. Die Beziehungen zwischen diesen Komponenten sind nichtlinear und dynamisch. Somit sind biologische Netzwerke typischerweise hochkomplex. Die Inferenz, d. h. die Rekonstruktion komplexer Netzwerke aus vorhandenen Daten und verfügbarem Wissen, ist nicht nur numerisch aufwändig (NP-schwer), sondern solche Netzwerk sind auch oft nicht eindeutig identifizierbar. Dieses Problem besteht bei der Inferenz vollgenomischer genregulatorischer Netzwerke aufgrund ihrer Komplexität einerseits und der beschränkten Zahl und Qualität (Messfehler) der Messdaten sowie der mangelhaften Vollständigkeit des verfügbaren Vorwissens andererseits. Um solche nicht identifizierbaren Netzwerke identifizierbar zu gestalten, muss entweder die Zahl und Qualität der Messdaten erhöht oder die Komplexität des Netzwerkmodells reduziert werden. Da die Anzahl und Qualität der Messdaten beschränkt ist (bedingt durch die praktisch verfügbaren Ressourcen und Techniken), kommt der Reduktion der Komplexität die entscheidende Aufgabe bei der Netzwerkinferenz in der Systembiologie zu. Die Reduktion der Komplexität kann auf verschiedene Weise geschehen:

Reduktion der Zahl der Knoten
Reduktion der Zahl der Kanten
Vereinfachung der Funktionen, die die Kanten repräsentieren

Diese Vereinfachungen stehen im Konflikt mit dem Ganzheitlichkeitsanspruch der Systembiologie.

Zu 1. Systembiologie hat den Anspruch ein biologisches System in seiner Gesamtheit zu untersuchen. Jede Reduktion der Zahl der Knoten, d. h. der einbezogenen Komponenten (Gene, Proteine, Metabolite u. a.) beruht auf Hypothesen oder auf bewussten Beschränkungen (oder – falls vorhanden – auf erkannten Gesetzmäßigkeiten). Eine typische Beschränkung besteht darin, dass nur differenziell exprimierte Gene als Knoten in Betracht gezogen werden. Ferner werden in gleicher Weise exprimierte oder regulierte (ko-regulierte) Gene mittels der Clusteranalyse in Gruppen[4] oder mittels Vorwissen über die Genfunktion und -regulation zu Modulen[3] zusammengefasst (Merkmalsselektion). Die Gruppen oder Module bilden dann die Knoten des Netzwerks.

Zu 2. Für die Reduktion der für die Netzwerkinferenz freigegebenen Kanten wurden in der Systembiologie verschiedene Hypothesen bemüht. Nach einer dieser Hypothesen ist das genregulatorische Netzwerk nur spärlich (englisch sparse) vernetzt. Es wird dann als zusätzliches Kriterium bei der Netzwerkinferenz die Minimierung der Kantenanzahl berücksichtigt.

Zu 3. Die einfachste Funktion, um Kanten zu bewerten ist binär. Mit derartigen Booleschen Netzwerken gelingt – bei gegebener Knoten- und Kantenanzahl – die weitestgehende Reduktion der Komplexität. Das Problem liegt dann auf der Abbildung von i. d. R. reellwertigen Messwerten, z. B. Intensitäten der Genexpression, auf diese zwei Werte. Für eine etwas weniger schwerwiegende Vereinfachung der Funktionen, die die Kanten repräsentieren, werden anstelle nichtlinearer Differentialgleichungsysteme mit nichtlinearen zeitvariablen Funktionen lineare Differentialgleichungen verwendet – oder, noch weiter vereinfachend, Differenzengleichungen, die dann in ein algebraisches Gleichungssystem überführt werden.

Vorwissen für die Netzwerkinferenz

Im Falle biologischer Systeme ohne Reduktion der Komplexität, insbesondere bei vollgenomischen GRN, ist die Aufgabe der Netzwerkinferenz nicht nur schlecht konditioniert, sondern auch unterbestimmt, d. h. die Zahl der experimentellen Daten ist zu gering für eine eindeutige Identifikation der Netzwerk-Struktur und -Parameter. Da die Anzahl und Qualität der Messdaten nicht beliebig zu erhöhen ist, u. a. aufgrund finanzieller Beschränkungen, kommt neben der – im Sinne der Systembiologie problematischen – Reduktion der Komplexität der Berücksichtigung von Vorwissen eine entscheidende Rolle zu. Das Vorwissen bezieht sich dabei sowohl auf die Aggregation von Knoten (zu Clustern oder Modulen, s. o.) als auch auf die Kanten, also auf das vorhandene Wissen über die Zusammenhänge zwischen den Knoten. Im einfachsten Falle ist es faktisches oder hypothetisches Wissen über die Abwesenheit eines Zusammenhangs. Bei Tausenden Knoten eines GRN ist das Vorwissen über Millionen Kanten gefragt. Die Menge derartigen Wissens ist zwar in der Fachliteratur stetig steigend, aber für die Nutzung dieses Wissens in numerischen Algorithmen muss das Wissen maschinenlesbar, z. B. aus Datenbanken auslesbar, sein.

Beispielsweise wurde für die Inferenz eines GRN von Leberzellen das Vorwissen über Transkriptionsfaktoren und andere Regulatorproteine sowie deren DNA-Bindestellen aus mehreren Datenbanken (Gene Ontology, oPOSSUM, JASPAR, TRANSFAC, PathwayStudio) extrahiert.[5] Während Datenbanken für Protein-Protein-Interaktionen bei einigen biologischen Arten einen fortgeschrittenen Stand erreicht haben, sind derartige Datenbanken für Gen-Protein-Gen-Beziehungen, wie die hochwertige, weil manuell gepflegte Datenbank TRANSFAC, für fast alle Arten stark lückenhaft oder sie enthalten unsichere, weil automatisch generierte hypothetische und nicht experimentell validierte Einträge. Dies ist begründet vor allem dadurch, dass die Gen-Protein-Gen-Beziehungen vermittelt über die Genexpression (Transkription, RNA-Prozessierung, Translation, Proteinreifung) und Protein-DNA-Wechselwirkungen an Transkriptionsfaktorbindestellen ihrerseits komplex, dynamisch und nichtlinear sind. Mit jeder erfolgten und zuverlässigen Inferenz eines GRN wächst allerdings das Wissen, das für nachfolgende Netzwerkinferenz mit neuen Messdaten eingesetzt werden kann.

Validierung der Netzwerkmodelle

Da sowohl die Messdaten als auch oft das Vorwissen mit Fehlern und Unsicherheiten behaftet sind sowie ein Netzwerkmodell nur unvollkommen die Eigenschaften eines realen Systems abbildet, muss das inferierte Netzwerkmodell validiert werden. Hier unterscheidet man zwischen der internen und der externen Validität. Ohne weiteren experimentellen Aufwand ist die interne Validität auf den gegebenen Mengen von Messdaten und Vorwissen mittels einer Resampling-Methode, z. B. mittels Kreuzvalidierung, zu bestimmen.[6]

Entscheidend für die Qualität eines inferierten Netzwerkmodells ist die Verallgemeinerungsfähigkeit, d. h. die Vorhersagegüte für das System unter veränderten (experimentellen) Bedingungen. Dieser Test geschieht dadurch, dass mittels Simulation des Netzwerkmodells Vorhersagen unter veränderten Bedingungen getroffen werden, die nachträglich experimentell realisiert werden und dabei erneut experimentelle Daten gemessen und mit dem vorhergesagten Systemverhalten verglichen werden.[7] Aufgrund der unvermeidlichen, aber nur hypothetisch begründeten Reduktion der Komplexität eines für die Netzwerkinferenz geeigneten Netzwerkmodells und auch aufgrund von möglichen Messfehlern sowie Unsicherheiten im verwendeten Vorwissen sind die mit bioinformatischen Methoden gewonnenen Schlussfolgerungen ihrerseits lediglich Hypothesen. Diese Hypothesen sind wertvoll für die fokussierte und damit ressourcensparende Planung von Experimenten, die der Verifikation der gewonnenen Hypothesen dienen.

Als Maß für die Validität wird z. B. die Fläche unter der Kurve (AUC – area under the curve) der ROC-Kurve (Receiver Operating Characteristic) verwendet.

Beispiele für Algorithmen zur Inferenz von Genregulationsnetzwerken

Die Fülle verschiedener Netzwerkinferenz-Algorithmen kann in folgende Kategorien gruppiert werden, wobei verschiedene Algorithmen auch parallel, in Kombinationen oder komplementär eingesetzt werden können[8]:

REVEAL und andere Algorithmen für Boolesche Netzwerke[9]

Statistische Methoden wie LASSO (Least Absolute Shrinkage and Selection Operator)[10][11] und LARS (Least-Angle Regression)[12]

Gewöhnliche Differentialgleichungssysteme in Verbindung mit Methoden der nichtlinearen Optimierung wie NetGenerator[4] oder in Verbindung mit Regressionsmethoden wie INFERELATOR[13]

Bayessches Netze[14] wie ScanBMA[15][16]

Graphische Gaußsche Modelle[17]

Informationstheorie-basierte Methoden wie ARACNE[18]

Die Eignung eines Algorithmus hängt vom Modelltyp, den verfügbaren Messdaten, dem zugänglichen Vorwissen, der Komplexität des Systems, insbesondere der Anzahl der Netzknoten und vor allem von der Zielstellung der Netzwerkinferenz ab. Seit 2006 werden im Rahmen des internationalen Projekts Dialogue on Reverse Engineering and Assessment Methods (DREAM) anhand vorgegebener Daten und ein (nur für die Jury) jeweils bekanntes System die jeweils leistungsfähigsten Algorithmen für die Netzwerkinferenz ermittelt.[19] Ein Ergebnis dieses Projekts ist die Erkenntnis, dass die Aggregation der Vorhersagen über mehrere Netzwerkmodelle, die mit verschiedenen Netzwerkinferenz-Algorithmen berechnet wurden, die Qualität und Robustheit der Vorhersagen verbessert.[20] Außerdem wurde gefunden, dass für die genomweite Netzwerkinferenz LASSO-Methoden am besten geeignet sind, sofern sie gut konfiguriert sind und die Messdaten sowie das Vorwissen in ausreichender Quantität und Qualität verfügbar sind – eine Voraussetzung, die für das Bakterium Escherichia coli gegeben ist. Boolesche Netze eignen sich bevorzugt zur Modellierung stationärer Situationen auf der Grundlage von Gen-Knockout-Daten und für die Identifikation von Signalwegen.

Literatur

M. Bansal, V. Belcastro, A. Ambesi-Impiombato, D. di Bernardo: How to infer gene networks from expression profiles. In: Molecular Systems Biology. Band 3, 2007, S. 78, doi:10.1038/msb4100120.
M. Hecker, S. Lambeck, S. Toepfer, E. van Someren, R. Guthke: Gene regulatory network inference: data integration in dynamic models - A review. In: BioSystems. Band 96, 2009, S. 86–103, doi:10.1016/j.biosystems.2008.12.004.
T. Ideker, N. J. Krogan: Differential network biology. In: Molecular Systems Biology. Band 8, 2012, S. 565, doi:10.1038/msb.2011.99, PMID 22252388.
S. R. Maetschke, P. B. Madhamshettiwar, M. J. Davis, M. A. Ragan: Supervised, semi-supervised and unsupervised inference of gene regulatory networks. In: Briefings in Bioinformatics. Band 15, 2014, S. 195–211, doi:10.1093/bib/bbt034.
P. Meyer, T. Cokelaer, D. Chandran, K. H. Kim, P. R. Loh, G. Tucker, M. Lipson, B. Berger, C. Kreutz, A. Raue, B. Steiert, J. Timmer, E. Bilal, H. M. Sauro, G. Stolovitzky, J. Saez-Rodriguez: Network topology and parameter estimation: from experimental design methods to gene regulatory network kinetics using a community based approach. In: BMC Systems Biology. Band 8, 2014, S. 13, doi:10.1186/1752-0509-8-13.
S. Hill, L. Heiser, T. Cokelaer, et al.: Inferring causal molecular networks: empirical assessment through a community-based effort. In: Nature Methods. Band 13, 2016, S. 310–318, doi:10.1038/nmeth.3773.
M. M. Saint-Antoine, A. Singh: Network inference in systems biology: recent developments, challenges, and applications. In: Current Opinion in Biotechnology. Band 63, 2020, S. 89–98, doi:10.1016/j.copbio.2019.12.002.

Einzelnachweise

M. Weber, S. G. Henkel, S. Vlaic, R. Guthke, E. J. van Zoelen, D. Driesch: Inference of dynamical gene-regulatory networks based on time-resolved multi-stimuli multi-experiment data applying NetGenerator V2.0. In: BMC Systems Biology. Band 7, 2013, S. 1, doi:10.1186/1752-0509-7-1, PMID 23280066.
J. Linde, S. Schulze, S. G. Henkel, R. Guthke: Data- and knowledge-based modeling of gene regulatory networks. An update. In: EXCLI Journal. Band 14, 2015, ISSN 1611-2156, S. 346–378, PMID 27047314.
S. Vlaic, T. Conrad, C. Tokarski-Schnelle, M. Gustafsson, U. Dahmen, R. Guthke, S. Schuster: ModuleDiscoverer: Identification of regulatory modules in protein-protein interaction networks. In: Scientific Reports. Band 8, Nr. 1, 2018, S. 433, doi:10.1038/s41598-017-18370-2, PMID 29323246.
R. Guthke, U. Möller, M. Hoffmann, F. Thies, S. Töpfer: Dynamic network reconstruction from gene expression data applied to immune response during bacterial infection. In: Bioinformatics. Band 21, 2005, S. 1626–1634, PMID 15613398.
S. Vlaic, W. Schmidt-Heck, M. Matz-Soja, E. Marbach, J. Linde, A. Meyer-Baese, S. Zellmer, R. Guthke, R. Gebhardt: The extended TILAR approach: a novel tool for dynamic modeling of the transcription factor network regulating the adaption to in vitro cultivation of murine hepatocytes. In: BMC Systems Biology. Band 6, 2012, S. 147, doi:10.1186/1752-0509-6-147.
S. M. Colby, R. S. McClure, C. C. Overall, et al.: Improving network inference algorithms using resampling methods. In: BMC Bioinformatics. Band 19, 2018, S. 376, doi:10.1186/s12859-018-2402-0.
J. Linde, P. Hortschansky, E. Fazius, A. Brakhage, R. Guthke, H. Haas: Regulatory interactions for iron homeostasis in Aspergillus fumigatus inferred by a Systems Biology approach. In: BMC Systems Biology. Band 6, 19. Januar 2012, S. 6, doi:10.1186/1752-0509-6-6.
Omid Abbaszadeh, Ali Reza Khanteymoori, Ali Azarpeyvand: Parallel Algorithms for Inferring Gene Regulatory Networks. A Review. In: Current Genomics. Band 19, S. 603–614, doi:10.2174/1389202919666180601081718.
S. Liang, S. Fuhrman, R. Somogyi: Reveal, a general reverse engineering algorithm for inference of genetic network architectur. In: Pacific Symposium on Biocomputing. Band 1998, 1998, S. 18–29, PMID 9697168.
R. Tibshirani: Regression shrinkage and selection via the Lasso. In: Journal of the Royal Statistical Society, Series B. Band 58, 1996, S. 267–288, JSTOR:2346178.
E. P. van Someren, B. L. Vaes, W. T. Steegenga, A. M. Sijbers, K. J. Dechering, M. J. Reinders: Least absolute regression network analysis of the murine osteoblast differentiation network. In: Bioinformatics. Band 22, 2006, S. 477, doi:10.1093/bioinformatics/bti816, PMID 16332709.
B. Efron, T. Hastie, I. Johnstone, R. Tibshirani: Least angle regression. In: Annals of Statistics. Band 32, 2004, S. 409–499, doi:10.1214/009053604000000067.
R. Bonneau, D.J. Reiss, P. Shannon, M. Facciotti, L. Hood, N. S. Baliga et al.: The Inferelator: an algorithm for learning parsimonious regulatory networks from systems-biology data sets de novo. In: Genome Biology. Band 7, Nr. 5, 2006, S. R36, PMID 16686963.
N. Friedman, M. Linial, I. Nachman, D. Pe'er: Using bayesian networks to analyze expression data. In: Journal of Computational Biology. Band 7, 2000, S. 601–620, doi:10.1089/106652700750050961, PMID 11108481.
W. C. Young, A. E. Raftery, K. Y. Yeung: Fast Bayesian inference for gene regulatory networks using ScanBMA. In: BMC Systems Biology. Band 8, 2014, S. 47, PMID 24742092.
X. Liang, W. C. Young, L.H. Hung, A. E. Raftery, K.Y. Yeung: Integration of Multiple Data Sources for Gene Network Inference Using Genetic Perturbation Data. In: Journal of Computational Biology. Band 26, Nr. 10, 2019, S. 1113‐1129, doi:10.1089/cmb.2019.0036.
A. Wille, P. Zimmermann, E. Vranová, A. Fürholz, O. Laule, S. Bleuler, L. Hennig, A. Prelic, P. von Rohr, L. Thiele, E. Zitzler, W. Gruissem, P. Bühlmann: Sparse graphical gaussian modeling of the isoprenoid gene network in Arabidopsis thaliana. In: Genome Biology. Band 5, Nr. 11, 2004, S. R92, doi:10.1186/gb-2004-5-11-r92, PMID 15535868.
K. Basso, A. A. Margolin, G. Stolovitzky, U. Klein, R. Dalla-Favera, A. Califano: Reverse engineering of regulatory networks in human B cells. In: Nature Genetics. Band 37, 2005, S. 382–390, doi:10.1038/ng1532, PMID 15778709.
Dialogue for Reverse Engineering Assessment and Methods (DREAM). Abgerufen am 17. Mai 2020.
D. Marbach, J. C. Costello, R. Küffner, N. M. Vega, R. J. Prill, D.M. Camacho, et al.: Wisdom of crowds for robust gene network inference. In: Nature Methods. Band 9, 2012, S. 796–804, doi:10.1038/nmeth.2016, PMID 22796662.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] M. Weber, S. G. Henkel, S. Vlaic, R. Guthke, E. J. van Zoelen, D. Driesch: Inference of dynamical gene-regulatory networks based on time-resolved multi-stimuli multi-experiment data applying NetGenerator V2.0. In: BMC Systems Biology. Band 7, 2013, S. 1, doi:10.1186/1752-0509-7-1, PMID 23280066.

[2] J. Linde, S. Schulze, S. G. Henkel, R. Guthke: Data- and knowledge-based modeling of gene regulatory networks. An update. In: EXCLI Journal. Band 14, 2015, ISSN 1611-2156, S. 346–378, PMID 27047314.

[Vlaic2018-3] S. Vlaic, T. Conrad, C. Tokarski-Schnelle, M. Gustafsson, U. Dahmen, R. Guthke, S. Schuster: ModuleDiscoverer: Identification of regulatory modules in protein-protein interaction networks. In: Scientific Reports. Band 8, Nr. 1, 2018, S. 433, doi:10.1038/s41598-017-18370-2, PMID 29323246.

[Guthke2005-4] R. Guthke, U. Möller, M. Hoffmann, F. Thies, S. Töpfer: Dynamic network reconstruction from gene expression data applied to immune response during bacterial infection. In: Bioinformatics. Band 21, 2005, S. 1626–1634, PMID 15613398.

[5] S. Vlaic, W. Schmidt-Heck, M. Matz-Soja, E. Marbach, J. Linde, A. Meyer-Baese, S. Zellmer, R. Guthke, R. Gebhardt: The extended TILAR approach: a novel tool for dynamic modeling of the transcription factor network regulating the adaption to in vitro cultivation of murine hepatocytes. In: BMC Systems Biology. Band 6, 2012, S. 147, doi:10.1186/1752-0509-6-147.

[6] S. M. Colby, R. S. McClure, C. C. Overall, et al.: Improving network inference algorithms using resampling methods. In: BMC Bioinformatics. Band 19, 2018, S. 376, doi:10.1186/s12859-018-2402-0.

[7] J. Linde, P. Hortschansky, E. Fazius, A. Brakhage, R. Guthke, H. Haas: Regulatory interactions for iron homeostasis in Aspergillus fumigatus inferred by a Systems Biology approach. In: BMC Systems Biology. Band 6, 19. Januar 2012, S. 6, doi:10.1186/1752-0509-6-6.

[8] Omid Abbaszadeh, Ali Reza Khanteymoori, Ali Azarpeyvand: Parallel Algorithms for Inferring Gene Regulatory Networks. A Review. In: Current Genomics. Band 19, S. 603–614, doi:10.2174/1389202919666180601081718.

[9] S. Liang, S. Fuhrman, R. Somogyi: Reveal, a general reverse engineering algorithm for inference of genetic network architectur. In: Pacific Symposium on Biocomputing. Band 1998, 1998, S. 18–29, PMID 9697168.

[10] R. Tibshirani: Regression shrinkage and selection via the Lasso. In: Journal of the Royal Statistical Society, Series B. Band 58, 1996, S. 267–288, JSTOR:2346178.

[11] E. P. van Someren, B. L. Vaes, W. T. Steegenga, A. M. Sijbers, K. J. Dechering, M. J. Reinders: Least absolute regression network analysis of the murine osteoblast differentiation network. In: Bioinformatics. Band 22, 2006, S. 477, doi:10.1093/bioinformatics/bti816, PMID 16332709.

[12] B. Efron, T. Hastie, I. Johnstone, R. Tibshirani: Least angle regression. In: Annals of Statistics. Band 32, 2004, S. 409–499, doi:10.1214/009053604000000067.

[13] R. Bonneau, D.J. Reiss, P. Shannon, M. Facciotti, L. Hood, N. S. Baliga et al.: The Inferelator: an algorithm for learning parsimonious regulatory networks from systems-biology data sets de novo. In: Genome Biology. Band 7, Nr. 5, 2006, S. R36, PMID 16686963.

[14] N. Friedman, M. Linial, I. Nachman, D. Pe'er: Using bayesian networks to analyze expression data. In: Journal of Computational Biology. Band 7, 2000, S. 601–620, doi:10.1089/106652700750050961, PMID 11108481.

[15] W. C. Young, A. E. Raftery, K. Y. Yeung: Fast Bayesian inference for gene regulatory networks using ScanBMA. In: BMC Systems Biology. Band 8, 2014, S. 47, PMID 24742092.

[16] X. Liang, W. C. Young, L.H. Hung, A. E. Raftery, K.Y. Yeung: Integration of Multiple Data Sources for Gene Network Inference Using Genetic Perturbation Data. In: Journal of Computational Biology. Band 26, Nr. 10, 2019, S. 1113‐1129, doi:10.1089/cmb.2019.0036.

[17] A. Wille, P. Zimmermann, E. Vranová, A. Fürholz, O. Laule, S. Bleuler, L. Hennig, A. Prelic, P. von Rohr, L. Thiele, E. Zitzler, W. Gruissem, P. Bühlmann: Sparse graphical gaussian modeling of the isoprenoid gene network in Arabidopsis thaliana. In: Genome Biology. Band 5, Nr. 11, 2004, S. R92, doi:10.1186/gb-2004-5-11-r92, PMID 15535868.

[18] K. Basso, A. A. Margolin, G. Stolovitzky, U. Klein, R. Dalla-Favera, A. Califano: Reverse engineering of regulatory networks in human B cells. In: Nature Genetics. Band 37, 2005, S. 382–390, doi:10.1038/ng1532, PMID 15778709.

[19] Dialogue for Reverse Engineering Assessment and Methods (DREAM). Abgerufen am 17. Mai 2020.

[20] D. Marbach, J. C. Costello, R. Küffner, N. M. Vega, R. J. Prill, D.M. Camacho, et al.: Wisdom of crowds for robust gene network inference. In: Nature Methods. Band 9, 2012, S. 796–804, doi:10.1038/nmeth.2016, PMID 22796662.