Schlussfolgerung
Schlussfolgerung, Schlussfolgern, Folgerung, Inferenz (aus lateinisch inferre „hineintragen“; „folgern“, „schließen“; englisch inference) oder Konklusion (lateinisch conclusio „Schlussfolgerung“) und Implikation sind in der Logik Bezeichnungen für mehrere eng miteinander verwandte Sachverhalte:
- Eine Schlussfolgerung ist erstens ein sprachliches Gebilde, das aus einer Reihe von wahrheitsfähigen Aussagen einerseits, den Prämissen oder Annahmen (zum Beispiel Axiomen oder wissenschaftlichen Hypothesen), und einer weiteren Aussage andererseits, der Konklusion, besteht. Ein solches Gebilde nennt man auch einen (logischen) Schluss oder ein Argument. Im Deutschen wird der Übergang zwischen Prämissen und Konklusion oft mit deshalb, darum, also, folglich oder auf Grund dessen eingeleitet. Man unterscheidet zwischen korrekten und inkorrekten Folgerungen (siehe dazu auch unten). Diese Unterscheidung ist für die Logik von zentraler Bedeutung; man kann die Logik geradezu als die Wissenschaft vom korrekten Folgern bezeichnen.
- In einem zweiten Sinne bezeichnet man als Schlussfolgerung einen Teil des eben angesprochenen sprachlichen Gebildes, nämlich die Konklusion. Für diese existieren auch die Synonyme Conclusio oder Schlusssatz. In der Rhetorik wird das Wort Konklusion auch allgemein für den Abschluss einer Rede gebraucht.
- Als Schlussfolgerung bezeichnet man zum Dritten das Ergebnis des Nachdenkens, also das (meist schrittweise) Erkennen von Folgerungen, bzw. das Durchführen eines Beweises. Diese Schlussfolgerungen können auch aus unbewussten kulturellen, sozialen oder religiösen Hintergrundannahmen gezogen werden.
In der Informatik und der Statistik wird die Schlussfolgerung auch gelegentlich mit dem sonst im Deutschen unüblichen Fremdwort Inferenz bezeichnet, wohl als Übersetzung des englischen inference (‚Schluss, Folgerung‘); meist aber wird das Wort Inferenz in der Informatik spezieller für solche Schlussfolgerungen verwendet, die automatisiert, d. h. computergestützt durch eine Inferenzmaschine, gezogen wurden.
Der logische Schluss wird mit dem Folgepfeil notiert.
Arten des logischen Schließens

A=>B ist die Regel, A die Bedingung und B die Konsequenz.Drei Arten des logischen Schließens werden unterschieden: Deduktion, Induktion und Abduktion. In aussagenlogischer bzw. syllogistischer Betrachtungsweise beschreiben diese drei unterschiedliche Fälle des Verhältnisses einer allgemeinen Regel, der Feststellung eines oder mehrerer Fälle, und der Subsumtion dieses Falls unter die Regel. Die Schlussarten unterscheiden sich darin, welchem dieser drei Elemente die Rolle einer Prämisse zugewiesen wird und welchem die der Folge oder Konsequenz. In der traditionellen Syllogistik sind diese Sätze immer Verhältnisse zwischen einem Ober-, einem Mittel- und einem Unterbegriff. Etwas schwieriger ist die Interpretation im Sinne einer Kausalität als Gesetz, Startbedingung und Wirkung.
- Deduktion ist der Schluss von der Regel und der Subsumtion auf den Fall.
- Induktion ist der Schluss von (mehreren) Fällen und ihrer Subsumtion unter den Mittelbegriff auf eine allgemeine Regel.
- Abduktion ist der Schluss von der Regel einem Fall die Subsumtion.
Dabei ist nur die Deduktion logisch zwingend; Induktion und Abduktion haben oft kein eindeutiges Ergebnis und können "naheliegend" sein, ihnen fehlt jedoch die Charakteristik, dass man von der Wahrheit der Prämissen sicher auf die Wahrheit der Konsequenz schließen kann. Bei der Abduktion kommt hinzu, dass gerade die Frage, welche Regel man als zweite Prämisse wählt, die besondere Leistung dieses Schlussverfahrens darstellt, während es bei der Induktion darum geht, zu wissen, über welche Eigenschaft (Unterbegriff) man generalisiert und ob die so generalisierte Regel einen inhaltlich sinnvollen Zusammenhang zwischen dem Mittel- und dem Oberbegriff stiftet. So ist es im unterstehenden Beispiel für eine "gelungene" Induktion wichtig, dass man annimmt, das der PKW als PKW bestimmten Regeln und Funktionsmechanismen unterliegt, und diese etwa nicht nur für ein bestimmtes Modell gelten. Die allgemeine Regel gilt in den Beispielfällen im Übrigen nur ceteris paribus.
Beispiele
| Wenn man bei einem PKW auf die Bremse tritt, verlangsamt sich die Fahrt. | |
| Bei diesem PKW wird auf die Bremse getreten. | |
| Deduktion | Dieser PKW verlangsamt seine Fahrt. |
| Dieser PKW verlangsamt seine Fahrt. | |
| Bei diesem PKW wird auf die Bremse getreten. | |
| Induktion | Wenn man bei einem PKW auf die Bremse tritt, verlangsamt sich die Fahrt. |
| Dieser PKW verlangsamt seine Fahrt. | |
| Wenn man bei einem PKW auf die Bremse tritt, verlangsamt sich die Fahrt. | |
| Abduktion | Bei diesem PKW wird auf die Bremse getreten. |
Korrektheit einer Schlussfolgerung
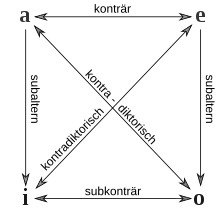
Eine erste Annäherung
In einer ersten Annäherung kann man sagen, dass eine Schlussfolgerung korrekt oder gültig ist, wenn es unmöglich ist, dass die Prämissen wahr sind, die Konklusion aber falsch ist – prägnant formuliert: Aus Wahrem folgt nur Wahres. Ein Beispiel:
- Prämissen: „Alle Menschen sind Bayern“, „Sokrates ist ein Mensch“
- Konklusion: „Sokrates ist Bayer“
Offenbar ist hier eine der Prämissen falsch, ebenso wie die Konklusion. Für die Gültigkeit eines Schlusses kommt es jedoch auf die tatsächliche Wahrheit der Prämissen nicht an, obiger Schluss ist gültig, da, wenn die Prämissen wahr wären, auch die Konklusion wahr wäre. (Wären nämlich tatsächlich alle Menschen Bayern, so wäre auch Sokrates einer, da er ein Mensch ist.) Sind also bei einem gültigen Schluss die Prämissen wahr, dann ist es auch die Konklusion. Ist jedoch mindestens eine Prämisse falsch, so kann die Konklusion wahr aber auch falsch sein. Ein Beispiel für eine Schlussfolgerung mit einer falschen Prämisse und einer wahren Konklusion wäre:
- Prämissen: „Alle Menschen sind Griechen“, „Sokrates ist ein Mensch“
- Konklusion: „Sokrates ist Grieche“.
Trotz seiner Eingängigkeit lässt der hier dargestellte Schlussbegriff „Aus Wahrem folgt nur Wahres“ Raum für unterschiedliche Interpretationen. So besteht sowohl intuitiv als auch philosophisch durchaus Uneinigkeit bezüglich der Gültigkeit unterschiedlicher Argumente beziehungsweise unterschiedlicher Arten von Argumenten. Als Beispiele seien die doppelte Negation (der Schluss aus „Es regnet nicht nicht“ auf „Es regnet“) und der Schluss von einer All- auf eine Existenzaussage (der Schluss von „Alle Schweine sind rosa“ auf „Es gibt rosa Schweine“) genannt, die unter anderem in Abhängigkeit vom konkreten Verständnis der Begriffe „nicht“ und „alle“ als gültig oder als ungültig betrachtet werden können.
Präzisierung
Etwas präziser kann man den Begriff der Korrektheit fassen, wenn man zwischen logischen und nicht-logischen Ausdrücken unterscheidet. Logische Ausdrücke sind Aussageverknüpfungen (Junktoren) wie „und“, „oder“ und „nicht“, mit denen eine oder mehrere Aussagen zu einer neuen, komplexeren Aussage verknüpft werden, sowie Quantoren wie „für alle“, „alle“, „jede/r“ (sog. Allquantoren) und „für manche“, „einige“, „es gibt“ (sog. Existenzquantoren); andere Ausdrücke heißen nicht-logisch. Ein Argument ist gültig, wenn jede Ersetzung eines oder mehrerer nicht-logischer Ausdrücke in ihm, bei der die Prämissen wahr sind, auch die Konklusion wahr macht („erfüllt“). Ersetzen wir im obigen Beispiel den nicht-logischen Ausdruck „Bayer“ beispielsweise durch „sterblich“ und „Mensch“ durch „Grieche“, erhalten wir:
- Prämissen: „Alle Griechen sind sterblich“, „Sokrates ist ein Grieche“
- Konklusion: „Sokrates ist sterblich“.
Hier sind beide Prämissen wahr, ebenso wie die Konklusion. Tatsächlich kann es in diesem Fall keine Ersetzung von nicht-logischen Ausdrücken geben, bei der beide Prämissen wahr sind, die Konklusion jedoch falsch ist. Hieraus ergibt sich auch ein Test, um die Ungültigkeit einer Schlussfolgerung nachzuweisen: Es ist eine Ersetzung der nicht-logischen Begriffe anzugeben, welche die Prämissen wahr macht, die Konklusion jedoch falsch. Man betrachte dazu beispielsweise folgendes ungültige Argument:
- Prämissen: „Einige Bayern sind Münchner“, „Einige Bayern sind Schwabinger“
- Konklusion: „Einige Münchner sind Schwabinger“
Hier sind beide Prämissen sowie auch die Konklusion wahr. Dennoch handelt es sich nicht um ein gültiges Argument, denn ersetzen wir „Schwabinger“ durch „Nürnberger“, so bleiben die Prämissen wahr, die Konklusion wird jedoch falsch.
Korrektheit in der formalen Logik
Um eine noch genauere und allgemeinere Charakterisierung der Korrektheit einer Schlussfolgerung bemüht sich die formale Logik. Wegen der größeren Komplexität und der Mehrdeutigkeit natürlicher Sprachen werden natürlichsprachliche Aussagen in Aussagen einer exakt definierten formalen Sprache übersetzt. Auf diesen formalen Objekten wird dann ein Ableitbarkeitsbegriff definiert, der meist durch das Zeichen symbolisiert ist. Die Motivation dabei ist oft die, dass genau dann zwischen den formalen Objekten eine Ableitbarkeitsbeziehung besteht, wenn die natürlichsprachlichen Gebilde, deren Übersetzungen sie darstellen, auseinander folgen.
Spätestens im Stadium der Formalisierung lassen sich die philosophischen und intuitiven Unterschiede im Verständnis von „Folgerung“ – und damit hinsichtlich dessen, welche Argumente gültig sind – nicht mehr überdecken. Entsprechend gibt es unterschiedliche, zueinander nicht äquivalente Ableitbarkeitsbegriffe, die die unterschiedlichen Spielarten des intuitiven und wissenschaftlichen Schlussbegriffs wiedergeben. Am häufigsten verwendet werden der klassische und der intuitionistische Ableitbarkeitsbegriff, deren Unterscheidung sowohl auf ein sehr unterschiedliches Verständnis der logischen Ausdrücke (z. B. der Junktoren „und“, „oder“ und „nicht“) als auch auf einen unterschiedlichen Wahrheitsbegriff zurückgeht.
Die Definition des Ableitbarkeitsbegriffs geschieht durch Schlussregeln und gegebenenfalls durch Axiome. Ein formales System, das Schlussregeln und Axiome festlegt, heißt Kalkül. Siehe hierzu auch den allgemeinen Artikel Beweis (Logik). Eine einführende Darstellung eines konkreten logischen Systems mit einer detaillierten Ausformulierung des Ableitbarkeitsbegriffs findet sich im Artikel Aussagenlogik. Zur automatischen Inferenz steht in der Informatik die Inferenzmaschine zur Verfügung.
Schlussverfahren
Schlussverfahren kommen bei verschiedenen Methoden in unterschiedlichen Bereichen zum Einsatz, z. B. Justiz-Syllogismus, probabilistisches Schließen, nichtmonotones Schließen usw.