Fläche unter der Kurve

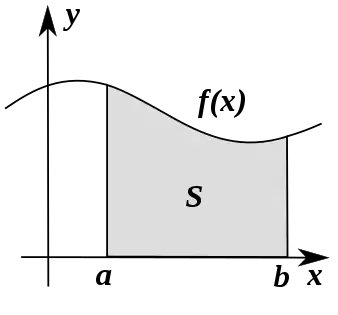
Die Fläche unter der Kurve[1] (englisch Area Under the Curve, kurz: AUC) entspricht mathematisch dem bestimmten Integral und ist eine elementare Anwendung der Integralrechnung.

AUC als bestimmtes Integral der Funktion f(x) im Intervall [a|b]

Naturwissenschaften

Der Begriff hat in den meisten Naturwissenschaften keine Anwendung gefunden, obwohl vielfach bestimmte Integrale verwendet werden (so ist beispielsweise die zurückgelegte Strecke das Integral der Geschwindigkeit über der Zeit) und ist auf die Pharmakokinetik begrenzt. In diesem Teilbereich der Pharmakologie wurde der Begriff als „Prinzip der korrespondierenden Flächen“ von Dost eingeführt.[2]

Medizin/Pharmakokinetik

Die intravenöse Bioverfügbarkeit ist per definitionem 100 %. Sind die AUCs bei beiden Applikationsarten gleich, entspricht daher die orale Bioverfügbarkeit ebenfalls 100 %.

In der Medizin und Pharmakologie bezeichnet Area under the curve (AUC) die Fläche unter der Konzentrations-Zeit-Kurve eines Pharmakons im Blut. Sie ist die Größe, durch welche die Bioverfügbarkeit eines Pharmakons ausgedrückt wird.[2] Die deutschsprachige Entsprechung „Fläche unter der Kurve“ hat sich in der Fachliteratur nicht durchgesetzt.[3][4][5]

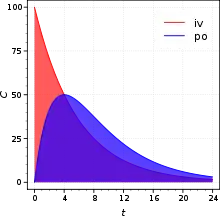
Man misst dazu die Konzentration des Arzneimittels in bestimmten Zeitintervallen im Blut nach Verabreichung. Für ein oral verabreichtes Medikament hat die aus der Messung resultierende Konzentrations-Zeit-Kurve einen typischen Verlauf, der sich aus der Geschwindigkeit des Übergangs des Arzneistoffs in den systemischen Blutkreislauf und aus der Kinetik des Ausscheidens zusammensetzt (blaue Fläche in der Abbildung, siehe auch Bateman-Funktion). Bei intravenöser Verabreichung ergibt sich eine Konzentrations-Zeit-Kurve, die praktisch nur durch die Ausscheidungskinetik bestimmt ist (rote Fläche).

Der Wert der AUC [Einheit: (Masse/Volumen)×Zeit] ist proportional der bioverfügbaren Menge des Arzneimittels, d. h. des Anteils an der insgesamt verabreichten Dosis (D), die in den Blutkreislauf kommt, unabhängig von der Applikationsart. Für einen intravenös verabreichten Stoff ist die Bioverfügbarkeit (F) per Definition 100 %. Ist bei oraler Gabe eines Medikaments die AUC gleich groß wie bei intravenöser Gabe, beträgt die Bioverfügbarkeit auch 100 %, ist sie geringer, ist auch die Bioverfügbarkeit entsprechend geringer.

F=100\cdot {\frac {AUC_{po}\cdot D_{iv}}{AUC_{iv}\cdot D_{po}}}

Berechnung aus Parametern eines pharmakokinetischen Modells

Am Beispiel der Bateman-Funktion (Konzentrationen nach oraler Verabreichung im Einkompartimentmodell)

C(t)={\frac {fD}{V}}{\frac {k_{a}}{k_{a}-k_{el}}}\left(e^{-k_{el}t}-e^{-k_{a}t}\right)

ergibt sich die AUC durch Integration nach der Zeit.

AUC_{0-\infty }=\int \limits _{0}^{\infty }C(t)\,dt={\frac {fD}{V}}{\frac {k_{a}}{k_{a}-k_{el}}}\left({\frac {1}{k_{el}}}-{\frac {1}{k_{a}}}\right)={\frac {fD}{Vk_{el}}}

Jedes lineare Kompartimentsystem lässt sich auch empirisch als eine Summe von Exponentialtermen darstellen.

C(t)=\sum _{i=1}^{n}A_{i}\cdot e^{B_{i}t}

Generell gilt dabei

AUC_{0-\infty }=\int \limits _{0}^{\infty }C(t)\,dt=\sum _{i=1}^{n}{\frac {A_{i}}{B_{i}}}

Lineare Trapezregel

Zwischen den gemessenen Konzentrationen wird linear interpoliert; die AUC bis zum letzten Messzeitpunkt $t_{n}$ wird durch die Summation der Flächen von Trapezen approximiert.

AUC_{0-t_{n}}\approx {\frac {1}{2}}\sum _{i=1}^{n-1}(t_{i+1}-t_{i})(C_{i}+C_{i+1})

Mit Hilfe der geschätzten Eliminationskonstanten ${\widehat {k_{el}}}$ wird die Restfläche $AUC_{t_{n}-\infty }$ berechnet.

AUC_{0-\infty }\approx AUC_{0-t_{n}}+{\frac {C_{n}}{\widehat {k_{el}}}}

Die Konzentration beim letzten Abnahmezeitpunkt ist in der Regel wegen der Nähe zur analytischen Bestimmungsgrenze mit der größten Messunsicherheit behaftet. Eine alternative Methode der Restflächenberechnung verwendet daher anstatt der letzten gemessenen Konzentration $C_{n}$ ihren Schätzwert ${\widehat {C_{n}}}$ .

Log-lineare Trapezregel

Da die Konzentrationen im Bereich der Elimination einem exponentiellen Verlauf folgen, werden bei Anwendung der linearen Trapezregel die Teilflächen nach dem Zeitpunkt der maximalen Konzentration systematisch überschätzt. Abhilfe schafft die logarithmische Interpolation.

AUC_{0-t_{n}}\approx \sum _{i=1}^{n-1}(t_{i+1}-t_{i}){\frac {C_{i+1}-C_{i}}{\ln {\frac {C_{i+1}}{C_{i}}}}}

Die Methode ist allerdings bei $C_{i}=0$ oder $C_{i+1}=C_{i}$ nicht anwendbar (in diesen Fällen wird die entsprechende Teilfläche linear berechnet). Zur Vermeidung von Rundungsfehlern sollte die Methode bei $0{,}999<{\frac {C_{i+1}}{C_{i}}}<1{,}001$ ebenfalls in diesem Intervall durch die lineare Methode ersetzt werden. In der Praxis wird oft auch eine Kombination beider Methoden verwendet, wobei bei ansteigenden oder gleichbleibenden Konzentration die lineare Trapezregel und bei abnehmenden die log-lineare angewendet wird.

Alternative Verfahren

Andere Methoden[6][7][8] der numerischen Integration wie etwa die Simpsonregel, kubische Splines und Lagrange-Polynome haben sich in der pharmakokinetischen Praxis nicht durchgesetzt und sind in kommerziellen Softwarepaketen nicht verfügbar.

Psychologische Diagnostik

Der Parameter Area under the curve (AUC) wird in der Psychologischen Diagnostik verwendet um bspw. die Wahrscheinlichkeit bestimmter Score-Intervalle bei einem psychometrischen Test zu bestimmen, als Effektgrösse bei ROC-Analysen,[9] zur Bestimmung der Trennschärfe, der diskriminativen Validität eines Instruments etc.

Einzelnachweise

Lothar Sachs, Jürgen Hedderich: Angewandte Statistik: Methodensammlung mit R. 8., überarb. und erg. Auflage. Springer Spektrum, Berlin/Heidelberg 2018, ISBN 978-3-662-56657-2, S. 669.
K. Aktories, U. Förstermann, F. Hofmann und K. Starke: Allgemeine und spezielle Pharmakologie und Toxikologie. 10. Auflage. München, Elsevier 2009. ISBN 978-3-437-42522-6
Wolfgang A. Knorre: Pharmakokinetik. Theoretische Grundlagen und praktische Anwendungen. Friedr. Vieweg und Sohn, Braunschweig/Wiesbaden 1981, ISBN 3-528-06862-0.
L. Dettli, J.W. Faigle, H. Hess, G.F. Kahl, F. Langenbucher, J. Meier, E. Mutschler, E. Nüesch, H. Rettig: Biopharmazie. Theorie und Praxis der Pharmakokinetik. Georg Thieme Verlag, Stuttgart/New York 1981, ISBN 3-13-603101-6.
Ernst Glaser: Pharmakokinetik. Grundlagen, lineare Modelle, Rechenverfahren, Auswertemethoden. pmi-Verlag, Frankfurt am Main 1985, ISBN 3-89119-011-5.
K. C. Yeh, K. C. Kwan: A Comparison of Numerical Integrationg Algorithms by Trapezoidal, Lagrange, and Spline Approximation. In: Journal of Pharmacokinetics and Biopharmarmaceutics. Band 6, Nr. 1, 1978, S. 79–89, doi:10.1007/BF01066064 (englisch).
K. C. Yeh, R. D. Small: Pharmacokinetic evaluation of stable piecewise cubic polynomials as numerical integration functions. In: Journal of Pharmacokinetics and Biopharmarmaceutics. Band 16, Nr. 6, 1989, S. 721–740, doi:10.1007/BF01062126 (englisch).
Robert D. Purves: Optimum Numerical Integration Methods for Estimation of Area-Under-the-Curve (AUC) and Area-under-the-Moment-Curve (AUMC). In: Journal of Pharmacokinetics and Biopharmarmaceutics. Band 20, Nr. 3, 1992, S. 211–226, doi:10.1007/BF01062525 (englisch).
Lothar Sachs, Jürgen Hedderich: Angewandte Statistik: Methodensammlung mit R. 8., überarb. und erg. Auflage. Springer Spektrum, Berlin/Heidelberg 2018, ISBN 978-3-662-56657-2, S. 566.

Literatur

Aktories, Förstermann, Hofmann (Hrsg.): Allgemeine und Spezielle Pharmakologie und Toxikologie (begründet von Forth, Henschler, Rummel). 9. Auflage 2004, Elsevier Urban & Fischer Verlag, ISBN 978-3-437-42521-9
Johan Gabrielsson, Dan Weiner: Pharmacokinetic & Pharmacodynamic Data Analysis. Concepts and Applications. 4. Auflage. Swedish Pharmaceutical Press, Stockholm 2007, ISBN 978-91-976510-0-4, 2.8 Non-Compartmental Analysis, S. 161–180 (englisch).
Milo Gibaldi, Donald Perrier: Pharmacokinetics. In: Drugs and the Pharmaceutical Sciences. 2. Auflage. Volume 15. Marcel Dekker, Inc., New York, Basel 1982, ISBN 0-8247-1042-8, Kap. 11, S. 409–417 (englisch).
Günther Pabst: Parameters for Compartment-free Pharmacokinetics. Standardisation of Study Design, Data Analysis and Reporting. Hrsg.: Willi Cawello. Shaker Verlag, Aachen 1999, ISBN 3-8265-4767-5, 5. Area under the concentration-time curve, S. 65–80 (englisch).
Malcolm Rowland, Thomas N. Tozer: Clinical Pharmacokinetics. Concepts and Applications. 4. Auflage. Lippincott Williams & Wilkins, a Wolters Kluwer business, Baltimore, Philadelphia 2010, ISBN 978-0-7817-5009-7, Appendix A, S. 687–690 (englisch).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Lothar Sachs, Jürgen Hedderich: Angewandte Statistik: Methodensammlung mit R. 8., überarb. und erg. Auflage. Springer Spektrum, Berlin/Heidelberg 2018, ISBN 978-3-662-56657-2, S. 669.

[aktories10-2] K. Aktories, U. Förstermann, F. Hofmann und K. Starke: Allgemeine und spezielle Pharmakologie und Toxikologie. 10. Auflage. München, Elsevier 2009. ISBN 978-3-437-42522-6

[Knorre-3] Wolfgang A. Knorre: Pharmakokinetik. Theoretische Grundlagen und praktische Anwendungen. Friedr. Vieweg und Sohn, Braunschweig/Wiesbaden 1981, ISBN 3-528-06862-0.

[Dettli_et_al-4] L. Dettli, J.W. Faigle, H. Hess, G.F. Kahl, F. Langenbucher, J. Meier, E. Mutschler, E. Nüesch, H. Rettig: Biopharmazie. Theorie und Praxis der Pharmakokinetik. Georg Thieme Verlag, Stuttgart/New York 1981, ISBN 3-13-603101-6.

[Glaser-5] Ernst Glaser: Pharmakokinetik. Grundlagen, lineare Modelle, Rechenverfahren, Auswertemethoden. pmi-Verlag, Frankfurt am Main 1985, ISBN 3-89119-011-5.

[YehKwan-6] K. C. Yeh, K. C. Kwan: A Comparison of Numerical Integrationg Algorithms by Trapezoidal, Lagrange, and Spline Approximation. In: Journal of Pharmacokinetics and Biopharmarmaceutics. Band 6, Nr. 1, 1978, S. 79–89, doi:10.1007/BF01066064 (englisch).

[YehSmall-7] K. C. Yeh, R. D. Small: Pharmacokinetic evaluation of stable piecewise cubic polynomials as numerical integration functions. In: Journal of Pharmacokinetics and Biopharmarmaceutics. Band 16, Nr. 6, 1989, S. 721–740, doi:10.1007/BF01062126 (englisch).

[Purves-8] Robert D. Purves: Optimum Numerical Integration Methods for Estimation of Area-Under-the-Curve (AUC) and Area-under-the-Moment-Curve (AUMC). In: Journal of Pharmacokinetics and Biopharmarmaceutics. Band 20, Nr. 3, 1992, S. 211–226, doi:10.1007/BF01062525 (englisch).

[9] Lothar Sachs, Jürgen Hedderich: Angewandte Statistik: Methodensammlung mit R. 8., überarb. und erg. Auflage. Springer Spektrum, Berlin/Heidelberg 2018, ISBN 978-3-662-56657-2, S. 566.