Kreuzvalidierungsverfahren
Kreuzvalidierungsverfahren sind auf Resampling basierende Testverfahren der Statistik, die z. B. im Data-Mining die zuverlässige Bewertung von Maschinen gelernten Algorithmen erlauben. Es wird unterschieden zwischen der einfachen Kreuzvalidierung, der stratifizierten Kreuzvalidierung und der Leave-One-Out-Kreuzvalidierung.
Problemstellung
Um einen verlässlichen Wert für die Anpassungsgüte (Qualität) eines statistischen Modells zu bekommen, gibt es in der Statistik verschiedene Verfahren. In der Regel werden dafür Kennzahlen benutzt, z. B. das (korrigierte) Bestimmtheitsmaß in der linearen Regression oder das Akaike- oder Bayes-Informationskriterium bei Modellen basierend auf der Maximum-Likelihood-Methode. Zum Teil basieren solche Kennzahlen auf asymptotischer Theorie, d. h., sie können nur für große Stichprobenumfänge verlässlich geschätzt werden. Ihre Schätzung bei kleinen Stichprobenumfängen ist daher problematisch. Oft ist auch die exakte Zahl der zu schätzenden Parameter, die für die Kennzahl benötigt wird, nicht berechenbar; ein Beispiel hierfür ist die nichtparametrische Statistik.
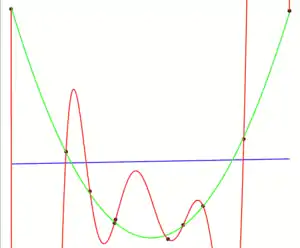
Des Weiteren gibt es das Problem, dass zu hoch parametrisierte Modelle dazu tendieren, sich zu stark an die Daten anzupassen. Ein Beispiel ist die Polynominterpolation. Hat man Beobachtungen , kann man ein Interpolationspolynom bestimmen, so dass für alle gilt. Zwischen den Beobachtungspunkten werden die Daten jedoch sehr schlecht interpoliert (sogenannte Überanpassung). Würde man nun den Fehler (in-sample error) berechnen, so würde man die Modellqualität überschätzen.
Um den zuvor genannten Problemen zu entgehen, wird der Datensatz in zwei Teile geteilt. Mit dem ersten Teil werden nur die Modellparameter geschätzt und auf Basis des zweiten Teils wird der Modellfehler berechnet (out-of-sample error). Die Verallgemeinerung dieses Verfahrens sind die Kreuzvalidierungsverfahren.
Einfache Kreuzvalidierung

Die zur Verfügung stehende Datenmenge, bestehend aus Elementen, wird in möglichst gleich große Teilmengen aufgeteilt. Nun werden Testdurchläufe gestartet, bei denen die jeweils -te Teilmenge als Testmenge und die verbleibenden Teilmengen als Trainingsmengen verwendet werden. Die Gesamtfehlerquote errechnet sich als Durchschnitt aus den Einzelfehlerquoten der Einzeldurchläufe. Diese Testmethode nennt man k-fache Kreuzvalidierung.
Stratifizierte Kreuzvalidierung
Aufbauend auf der einfachen k-fachen Kreuzvalidierung, achtet die k-fache stratifizierte Kreuzvalidierung darauf, dass jede der k Teilmengen eine annähernd gleiche Verteilung besitzt. Dadurch wird die Varianz der Abschätzung verringert.
Leave-One-Out-Kreuzvalidierung
Bei der Leave-One-Out-Kreuzvalidierung (engl. leave-one-out cross validation LOO-CV) handelt es sich um einen Spezialfall der k-fachen Kreuzvalidierung, bei der k = N (N = Anzahl der Elemente). Somit werden N Durchläufe gestartet und deren Einzelfehlerwerte ergeben als Mittelwert die Gesamtfehlerquote.
Ein Nachteil dieser Methode ist, dass eine Stratifizierung der Teilmengen, wie bei der stratifizierten Kreuzvalidierung, nicht mehr möglich ist. Dadurch kann es in Extremfällen dazu kommen, dass dieses Testverfahren falsche Fehlerwerte liefert. Beispiel: Eine vollständig zufällige Datenmenge bei gleichmäßiger Verteilung und nur zwei Klassen würde zu einem LOO-CV mit einer Genauigkeit von etwa 0 führen. Aus N Elementen werden zum Training N / 2 Elemente der einen Klasse und N / 2 − 1 Elemente der anderen Klasse verwendet. Die wahre Fehlerquote betrüge jeweils 50 %. Da der Klassifikator immer den Gegenpart zur Mehrheitsklasse der Testdaten prognostiziert, liefert der Test für jede Klasse die falsche Vorhersage. Die daraus ermittelte Gesamtfehlerquote beträgt also 100 %.[1]
Ein weiterer Nachteil ist, dass die Anzahl der Trainingsläufe zu einem sehr hohen Rechenaufwand führt.
Wiederholtes zufälliges Subsampling
Beim wiederholten zufälligen Subsampling (repeated random sub-sampling) werden wiederholt zufällige Unterstichproben gezogen. Ein Beispielalgorithmus, welcher Subsampling nutzt, ist der RANSAC-Algorithmus[2]
Anwendungsbeispiel
Ein Psychologe entwickelt einen neuen Test, mit dem er Depressivität messen will.
Um zu überprüfen, wie gut der Test das zu messende Merkmal (Depressivität) misst, lässt er in einem ersten Schritt eine große Gruppe von Personen, bei denen die jeweilige Ausprägung des Merkmals bekannt ist (vorher durch Experten oder einen anderen Test bestimmt), an diesem Test teilnehmen.
Im nächsten Schritt unterteilt er die große Gruppe in zwei zufällig zusammengestellte Untergruppen (bzw. k-Teilmengen, siehe weiter oben), nennen wir sie Untergruppe A und Untergruppe B. Der Psychologe benutzt nun die Daten der Untergruppe A, um mit ihnen eine Vorhersagegleichung für das Merkmal, das der Test messen soll, zu erstellen. D. h., er bildet eine Regel, nach der aus den Testdaten einer Person Rückschlüsse auf die Ausprägung des gesuchten Merkmals bei ihr gezogen werden können. Diese Vorhersagegleichung wendet er nun auf alle Mitglieder der Untergruppe B an und versucht, aus den Testdaten von Untergruppe B, mithilfe der an Untergruppe A entwickelten Vorhersagegleichung, auf deren jeweilige Ausprägung des Merkmals zu schließen.
Anschließend wird der Prozess umgekehrt, also B genutzt um A vorherzusagen. Die Kreuzvalidierung besteht darin den Durchschnitt der Genauigkeit beider Vorhersagen zu bilden. Dieses Verfahren kann mit beliebig vielen Untergruppen(k) durchgeführt werden, wobei k-1 Gruppen genutzt werden um die verbleibende Test-Gruppe vorherzusagen.
Einzelnachweise
- Ian H. Witten, Eibe Frank und Mark A. Hall: Data Mining: Practical Machine Learning Tools and Techniques. 3. Auflage. Morgan Kaufmann, Burlington, MA 2011, ISBN 978-0-12-374856-0 (waikato.ac.nz).
- Cantzler, H. "Random sample consensus (ransac)." Institute for Perception, Action and Behaviour, Division of Informatics, University of Edinburgh (1981). http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.106.3035&rep=rep1&type=pdf