Clusteranalyse

Unter Clusteranalysen (Clustering-Algorithmen, gelegentlich auch: Ballungsanalyse) versteht man Verfahren zur Entdeckung von Ähnlichkeitsstrukturen in (meist relativ großen) Datenbeständen. Die so gefundenen Gruppen von „ähnlichen“ Objekten werden als Cluster bezeichnet, die Gruppenzuordnung als Clustering. Die gefundenen Ähnlichkeitsgruppen können graphentheoretisch, hierarchisch, partitionierend oder optimierend sein. Die Clusteranalyse ist eine wichtige Disziplin des Data-Mining, des Analyseschritts des Knowledge-Discovery-in-Databases-Prozesses. Bei der Clusteranalyse ist das Ziel, neue Gruppen in den Daten zu identifizieren (im Gegensatz zur Klassifikation, bei der Daten bestehenden Klassen zugeordnet werden). Man spricht von einem „uninformierten Verfahren“, da es nicht auf Klassen-Vorwissen angewiesen ist. Diese neuen Gruppen können anschließend beispielsweise zur automatisierten Klassifizierung, zur Erkennung von Mustern in der Bildverarbeitung oder zur Marktsegmentierung eingesetzt werden (oder in beliebigen anderen Verfahren, die auf ein derartiges Vorwissen angewiesen sind).

Ergebnis einer Clusteranalyse mit Normalverteilungen

Die zahlreichen Algorithmen unterscheiden sich vor allem in ihrem Ähnlichkeits- und Gruppenbegriff, ihrem Cluster-Modell, ihrem algorithmischen Vorgehen (und damit ihrer Komplexität) und der Toleranz gegenüber Störungen in den Daten. Ob das von einem solchen Algorithmus generierte „Wissen“ nützlich ist, kann jedoch in der Regel nur ein Experte beurteilen. Ein Clustering-Algorithmus kann unter Umständen vorhandenes Wissen reproduzieren (beispielsweise Personendaten in die bekannten Gruppen „männlich“ und „weiblich“ unterteilen) oder auch für den Anwendungszweck nicht hilfreiche Gruppen generieren. Die gefundenen Gruppen lassen sich oft auch nicht verbal beschreiben (z. B. „männliche Personen“), gemeinsame Eigenschaften werden in der Regel erst durch eine nachträgliche Analyse identifiziert. Bei der Anwendung von Clusteranalyse ist es daher oft notwendig, verschiedene Verfahren und verschiedene Parameter zu probieren, die Daten vorzuverarbeiten und beispielsweise Attribute auszuwählen oder wegzulassen.

Beispiel

Angewendet auf einen Datensatz von Fahrzeugen könnte ein Clustering-Algorithmus (und eine nachträgliche Analyse der gefundenen Gruppen) beispielsweise folgende Struktur liefern:

Fahrzeuge

Fahrräder

Dabei ist Folgendes zu beachten:

Der Algorithmus selbst liefert keine Interpretation („LKW“) der gefundenen Gruppen. Hierzu ist eine separate Analyse der Gruppen notwendig.
Ein Mensch würde eine Fahrradrikscha als Untergruppe der Fahrräder ansehen. Für einen Clusteringalgorithmus aber sind 3 Räder oft ein signifikanter Unterschied, den sie mit einem Dreirad-Rollermobil teilen.
Die Gruppen sind oftmals nicht „rein“, es können also beispielsweise kleine LKW in der Gruppe der PKW sein.
Es treten oft zusätzliche Gruppen auf, die nicht erwartet wurden („Polizeiautos“, „Cabrios“, „rote Autos“, „Autos mit Xenon-Scheinwerfern“).
Manche Gruppen werden nicht gefunden, beispielsweise „Motorräder“ oder „Liegeräder“.
Welche Gruppen gefunden werden, hängt stark vom verwendeten Algorithmus, Parametern und verwendeten Objekt-Attributen ab.
Oft wird auch nichts (sinnvolles) gefunden.
In diesem Beispiel wurde nur bekanntes Wissen (wieder-)gefunden – als Verfahren zur „Wissensentdeckung“ ist die Clusteranalyse hier also gescheitert.

Geschichte

Historisch gesehen stammt das Verfahren aus der Taxonomie in der Biologie, wo über eine Clusterung von verwandten Arten eine Ordnung der Lebewesen ermittelt wird. Allerdings wurden dort ursprünglich keine automatischen Berechnungsverfahren eingesetzt. Inzwischen können zur Bestimmung der Verwandtschaft von Organismen unter anderem ihre Gensequenzen verglichen werden (Siehe auch: Kladistik). Später wurde das Verfahren für die Zusammenhangsanalyse in die Sozialwissenschaften eingeführt, weil es sich wegen des in den Gesellschaftswissenschaften in der Regel niedrigen Skalenniveaus der Daten in diesen Disziplinen besonders eignet.[1]

Prinzip/Funktionsweise

Mathematische Modellierung

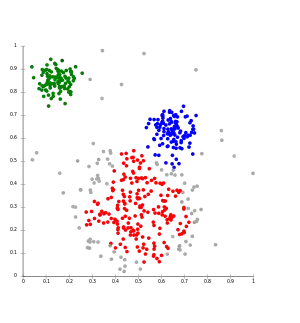
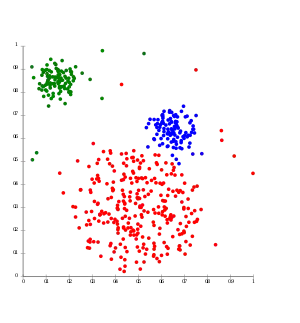
Die Eigenschaften der zu untersuchenden Objekte werden mathematisch als Zufallsvariablen aufgefasst. Sie werden in der Regel in Form von Vektoren als Punkte in einem Vektorraum dargestellt, deren Dimensionen die Eigenschaftsausprägungen des Objekts bilden. Bereiche, in denen sich Punkte anhäufen (Punktwolke), werden Cluster genannt. Bei Streudiagrammen dienen die Abstände der Punkte zueinander oder die Varianz innerhalb eines Clusters als sogenannte Proximitätsmaße, welche die Ähnlichkeit bzw. Unterschiedlichkeit zwischen den Objekten zum Ausdruck bringen.

Ein Cluster kann auch als eine Gruppe von Objekten definiert werden, die in Bezug auf einen berechneten Schwerpunkt eine minimale Abstandssumme haben. Dazu ist die Wahl eines Distanzmaßes erforderlich. In bestimmten Fällen sind die Abstände (bzw. umgekehrt die Ähnlichkeiten) der Objekte untereinander direkt bekannt, so dass sie nicht aus der Darstellung im Vektorraum ermittelt werden müssen.

Grundsätzliche Vorgehensweise

In einer Gesamtmenge/-gruppe mit unterschiedlichen Objekten werden die Objekte, die sich ähnlich sind, zu Gruppen (Clustern) zusammengefasst.

Als Beispiel sei folgende Musikanalyse gegeben. Die Werte ergeben sich aus dem Anteil der Musikstücke, die der Nutzer pro Monat online kauft.

	Person 1	Person 2	Person 3
Pop	2	1	8
Rock	10	8	1
Jazz	3	3	1

In diesem Beispiel würde man die Personen intuitiv in zwei Gruppen einteilen. Gruppe1 besteht aus Person 1&2 und Gruppe 2 besteht aus Person 3. Das würden auch die meisten Clusteralgorithmen machen. Dieses Beispiel ist lediglich aufgrund der gewählten Werte so eindeutig, spätestens mit näher zusammenliegenden Werten und mehr Variablen (hier Musikrichtungen) und Objekten (hier Personen) ist leicht vorstellbar, dass die Einteilung in Gruppen nicht mehr so trivial ist.

Etwas genauer und abstrakter ausgedrückt: Die Objekte einer heterogenen (beschrieben durch unterschiedliche Werte ihrer Variablen) Gesamtmenge werden mit Hilfe der Clusteranalyse zu Teilgruppen (Clustern/Segmenten) zusammengefasst, die in sich möglichst homogen (die Unterschiede der Variablen möglichst gering) sind. In unserem Musikbeispiel kann die Gruppe aller Musikhörer (eine sehr heterogene Gruppe) in die Gruppen der Jazzhörer, Rockhörer, Pophörer etc. (jeweils relativ homogen) unterteilt werden bzw. werden die Hörer mit ähnlichen Präferenzen zu der entsprechende Gruppe zusammengefasst.

Eine Clusteranalyse (z. B. bei der Marktsegmentierung) erfolgt dabei in folgenden Schritten:

Schritte zur Clusterbildung:

Variablenauswahl: Auswahl (und Erhebung) der für die Untersuchung geeigneten Variablen. Sofern die Variablen der Objekte/Elemente noch nicht bekannt/vorgegeben sind, müssen alle für die Untersuchung wichtigen Variablen bestimmt und anschließend ermittelt werden.
Proximitätsbestimmung: Wahl eines geeigneten Proximitätsmaßes und Bestimmung der Distanz- bzw. Ähnlichkeitswerte (je nach Proximitätsmaß) zwischen den Objekten über das Proximitätsmaß. Abhängig von der Art der Variablen bzw. der Skalenart der Variablen wird eine entsprechende Distanzfunktion zur Bestimmung des Abstandes (Distanz) zweier Elemente oder eine Ähnlichkeitsfunktion zur Bestimmung der Ähnlichkeit verwendet. Die Variablen werden zunächst einzeln verglichen und aus der Distanz der einzelnen Variablen die Gesamtdistanz (oder Ähnlichkeit) berechnet. Die Funktion zur Bestimmung von Distanz oder Ähnlichkeit wird auch Proximitätsmaß genannt. Der durch ein Proximitätsmaß ermittelte Distanz- bzw. Ähnlichkeitwert nennt sich Proximität. Werden alle Objekte miteinander verglichen, ergibt sich eine Proximitätsmatrix, welche jeweils zwei Objekten eine Proximität zuweist.
Clusterbildung: Bestimmung und Durchführung eines/der geeigneten Clusterverfahren(s), um anschließend mit Hilfe des/dieser Verfahrens Gruppen/Cluster bilden zu können (die Proximitätsmatrix wird hierdurch reduziert). Im Regelfall werden hierbei mehrere Verfahren kombiniert, z. B.:
- Finden von Ausreißern durch das Single-Linkage-Verfahren (hierarchisches Verfahren)
- Bestimmung der Clusterzahl durch das Ward-Verfahren (hierarchisches Verfahren)
- Bestimmung der Clusterzusammensetzung durch das Austauschverfahren (partitionierendes Verfahren)

Weitere Schritte der Clusteranalyse:

Bestimmung der Clusterzahl durch Betrachtung der Varianz innerhalb und zwischen den Gruppen. Hier wird bestimmt, wie viele Gruppen tatsächlich gebildet werden, denn bei der Clusterung selbst ist keine Abbruchbedingung vorgegeben. Z. B. wird bei einem agglomerativen Verfahren folglich so lange fusioniert, bis nur noch eine Gesamtgruppe vorhanden ist.
Interpretation der Cluster (abhängig von den inhaltlichen Ergebnissen, z. B. durch t-Wert)
Beurteilung der Güte der Clusterlösung (Bestimmung der Trennschärfe der Variablen, Gruppenstabilität)

Unterschiedliche Proximitätsmaße/Skalen

Die Skalen bezeichnen den Wertebereich, den die betrachtete(n) Variable(n) des Objektes annehmen kann/können. Je nachdem welche Art von Skala vorliegt, muss man ein passendes Proximitätsmaß verwenden. Es gibt drei Hauptkategorien von Skalen:

Binäre Skalen
die Variable kann zwei Werte annehmen, z. B. 0 oder 1, männlich oder weiblich.
Verwendete Proximitätsmaße (Beispiele):
- Jaccard-Koeffizient (Ähnlichkeitsmaß)
- Lance-Williams-Maß (Distanzmaß)
Nominale Skalen
die Variable kann unterschiedliche Werte annehmen, um eine qualitative Unterscheidung zu treffen, z. B. ob Pop, Rock oder Jazz bevorzugt wird.
Verwendete Proximitätsmaße (Beispiele):
- Chi-Quadrat-Maß (Distanzmaß)
- Phi-Quadrat-Maß (Distanzmaß)
Metrische Skalen
die Variable nimmt einen Wert auf einer vorher festgelegten Skala ein, um eine quantitative Aussage zu treffen, z. B. wie gerne eine Person Pop auf einer Skala von 1 bis 10 hört.
Verwendete Proximitätsmaße (Beispiele):
- Pearson-Korrelationskoeffizient (Ähnlichkeitsmaß)
- Euklidische Metrik (Distanzmaß)
- Minkowski-Metrik (Distanzmaß)

Formen der Gruppenbildung (Gruppenzugehörigkeit)

Es sind drei unterschiedliche Formen der Gruppenbildung (Gruppenzugehörigkeit) möglich. Bei den nichtüberlappenden Gruppen wird jedes Objekt nur einer Gruppe (Segment, Cluster) zugeordnet, bei den überlappenden Gruppen kann ein Objekt mehreren Gruppen zugeordnet werden, und bei den Fuzzygruppen gehört ein Element jeder Gruppe mit einem bestimmten Grad des Zutreffens an.

Nichtüberlappend

Formen der Gruppenbildung

Überlappend

Fuzzy

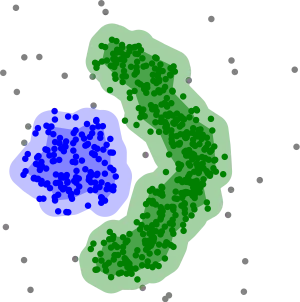
Man unterscheidet zwischen „harten“ und „weichen“ Clusteringalgorithmen. Harte Methoden (z. B. k-means, Spektrales Clustering, Kernbasierte Hauptkomponentenanalyse (kernel principal component analysis, kurz: kernel PCA)) ordnen jeden Datenpunkt genau einem Cluster zu, wohingegen bei weichen Methoden (z. B. EM-Algorithmus mit Gaußschen Mischmodellen (gaussian mixture models, kurz: GMMs)) jedem Datenpunkt für jeden Cluster ein Grad zugeordnet wird, mit der dieser Datenpunkt in diesem Cluster zugeordnet werden kann. Weiche Methoden sind insbesondere dann nützlich, wenn die Datenpunkte relativ homogen im Raum verteilt sind und die Cluster nur als Regionen mit erhöhter Datenpunktdichte in Erscheinung treten, d. h., wenn es z. B. fließende Übergänge zwischen den Clustern oder Hintergrundrauschen gibt (harte Methoden sind in diesem Fall unbrauchbar).

Unterscheidung der Clusterverfahren

Clusterverfahren lassen sich in graphentheoretische, hierarchische, partitionierende und optimierende Verfahren sowie in weitere Unterverfahren einteilen.

Partitionierende Verfahren
verwenden eine gegebene Partitionierung und ordnen die Elemente durch Austauschfunktionen um, bis die verwendete Zielfunktion ein Optimum erreicht. Zusätzliche Gruppen können jedoch nicht gebildet werden, da die Anzahl der Cluster bereits am Anfang festgelegt wird (vgl. hierarchische Verfahren).
Hierarchische Verfahren
gehen von der feinsten (agglomerativ bzw. bottom-up) bzw. gröbsten (divisiv bzw. top-down) Partition aus (vgl. Top-down und Bottom-up). Die gröbste Partition entspricht der Gesamtheit aller Elemente und die feinste Partition enthält lediglich ein Element bzw. jedes Element bildet seine eigene Gruppe/Partition. Durch Aufteilen bzw. Zusammenfassen lassen sich anschließend Cluster bilden. Einmal gebildete Gruppen können nicht mehr aufgelöst oder einzelne Elemente getauscht werden (vgl. partitionierende Verfahren). Agglomerative Verfahren kommen in der Praxis (z. B. bei der Marktsegmentierung im Marketing) sehr viel häufiger vor.

graphentheoretisch

divisiv

hierarchisch

agglomerativ

Clusterverfahren

Austauschverfahren

partitionierend

iterierte Minimaldistanzverfahren

optimierend

Zu beachten ist, dass man noch diverse weitere Verfahren und Algorithmen unterscheiden kann, unter anderem überwachte (supervised) und nicht-überwachte (unsupervised) Algorithmen oder modellbasierte Algorithmen, bei denen eine Annahme über die zugrundeliegende Verteilung der Daten gemacht wird (z. B. mixture-of-Gaussians model).

Verfahren

Es sind eine Vielzahl von Clustering-Verfahren in den unterschiedlichsten Anwendungsgebieten entwickelt worden. Man kann folgende Verfahrenstypen unterscheiden:

(zentrumsbasierte) partitionierende Verfahren,
hierarchische Verfahren,
dichte-basierte Verfahren,
gitter-basierte Verfahren und
kombinierte Verfahren.

Die ersten beiden Verfahrenstypen sind die klassischen Clusterverfahren, während die anderen Verfahren eher neueren Datums sind.

Partitionierende Clusterverfahren

Partitionierende Clusteranalyse

K-means teilt die Daten in Voronoi-Zellen, und nimmt an, dass die Cluster etwa gleich groß sind (hier nicht gerechtfertigt).

K-means kann dichtebasierte Cluster nicht gut trennen.

Normalverteilte Cluster können von EM-Clustering gut erkannt werden.

Nicht konvexe Cluster werden auch vom EM-Algorithmus nicht gut erkannt.

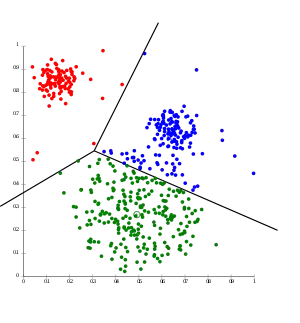
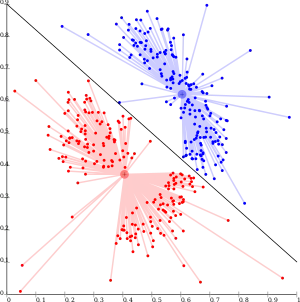
Die Gemeinsamkeit der partitionierenden Verfahren ist, dass zunächst die Zahl der Cluster $k$ festgelegt werden muss (Nachteil). Dann werden $k$ Clusterzentren bestimmt und diese iterativ solange verschoben, bis sich die Zuordnung der Beobachtungen zu den $k$ Clusterzentren nicht mehr verändert, wobei eine vorgegebene Fehlerfunktion minimiert wird. Ein Vorteil ist, dass Objekte während der Verschiebung der Clusterzentren ihre Clusterzugehörigkeit wechseln können.

K-Means-Algorithmus

Die Clusterzentren werden zufällig festgelegt und die Summe der quadrierten euklidischen Abstände der Objekte zu ihrem nächsten Clusterzentrum wird minimiert. Das Update der Clusterzentren geschieht durch Mittelwertbildung aller Objekte in einem Cluster.

k-Means++[2]: Als Clusterzentren werden auch zufällig Objekte so ausgewählt, so dass sie etwa uniform im Raum der Objekte verteilt sind. Dies führt zu einem schnelleren Algorithmus.
k-Median-Algorithmus: Hier wird die Summe der Manhattan-Distanzen der Objekte zu ihrem nächsten Clusterzentrum minimiert. Das Update der Clusterzentren geschieht durch die Berechnung des Medians aller Objekte in einem Cluster. Ausreißer in den Daten haben dadurch weniger Einfluss.
k-Medoids oder Partitioning Around Medoids (PAM)[3]: Die Clusterzentren sind hier immer Objekte. Durch Verschiebung von Clusterzentren auf ein benachbartes Objekt wird die Summe der Distanzen zum nächstgelegenen Clusterzentrum minimiert. Im Gegensatz zum k-Means Verfahren werden nur die Distanzen zwischen den Objekten benötigt und nicht die Koordinaten der Objekte.

Fuzzy-c-Means-Algorithmus[4]

Für jedes Objekt wird ein Zugehörigkeitsgrad zu einem Cluster berechnet, oft aus dem reellwertigen Intervall [0,1] (Zugehörigkeitsgrad=1: Objekt gehört vollständig zu einem Cluster, Zugehörigkeitsgrad=0: Objekt gehört nicht zu dem Cluster). Dabei gilt: je weiter ein Objekt vom Clusterzentrum entfernt ist, desto kleiner ist auch sein Zugehörigkeitsgrad zu diesem Cluster. Wie im k-Median-Verfahren werden die Clusterzentren dann verschoben, jedoch haben weit entfernte Objekte (kleiner Zugehörigkeitsgrad) einen geringen Einfluss auf die Verschiebung als nahe Objekte. Damit wird auch eine weiche Clusterzuordnung erreicht: Jedes Objekt gehört zu jedem Cluster mit einem entsprechenden Zugehörigkeitsgrad.

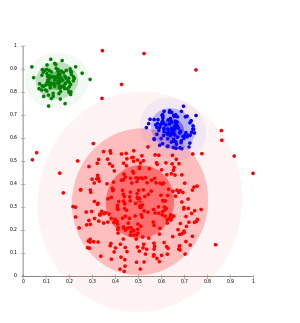
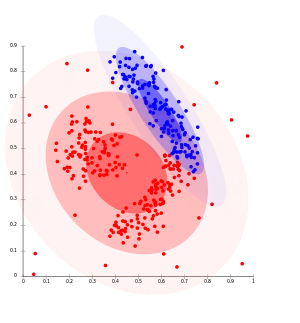
EM-Clustering[5]

Die Cluster werden als

k

multivariate Normalverteilungen modelliert. Mit Hilfe des EM-Algorithmus werden die unbekannten Parameter (

\mu _{i},\Sigma _{i}

mit

i=1,\ldots ,k

) der Normalverteilungen iterativ geschätzt. Im Gegensatz zu k-means wird damit eine weiche Clusterzuordnung erreicht: Mit einer gewissen Wahrscheinlichkeit gehört jedes Objekt zu jedem Cluster und jedes Objekt beeinflusst so die Parameter jeden Clusters.

Affinity-Propagation

Affinity-Propagation ist ein deterministischer Message-Passing-Algorithmus, welcher die optimalen Clusterzentren findet. Als Ähnlichkeitsfunktion kann je nach Art der Daten z. B. die negative euklidische Distanz verwendet werden. Abstände der Objekte zu ihrem nächsten Clusterzentrum werden minimiert. Das Update der Clusterzentren geschieht durch Berechnung der Responsibility und Availability sowie deren Summe, aller Objekte.

Hierarchische Clusterverfahren

Hierarchische Clusteranalyse

Single Linkage auf normalverteilten Daten. Durch den Single-Link-Effekt trennen sich die beiden größten Cluster erst bei insgesamt 35 Clustern.

Single Linkage mit dichtebasierten Clustern. Zusätzlich zu den zwei Clustern werden noch 18 weitere einelementige Cluster gefunden.

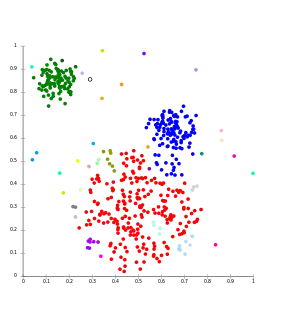
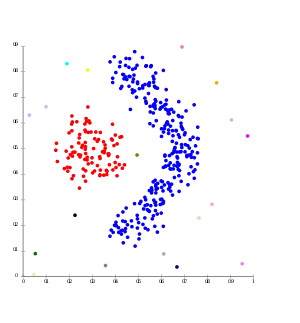
Als hierarchische Clusteranalyse bezeichnet man eine bestimmte Familie von distanzbasierten Verfahren zur Clusteranalyse. Cluster bestehen hierbei aus Objekten, die zueinander eine geringere Distanz (oder umgekehrt: höhere Ähnlichkeit) aufweisen als zu den Objekten anderer Cluster. Dabei wird eine Hierarchie von Clustern aufgebaut: auf der einen Seite ein Cluster, der alle Objekte enthält, und auf der anderen Seite so viele Cluster, wie man Objekte hat, d. h., jedes Cluster enthält genau ein Objekt. Man unterscheidet zwei wichtige Typen von Verfahren:

die divisiven Clusterverfahren, in dem zunächst alle Objekte als zu einem Cluster gehörig betrachtet werden und dann schrittweise die Cluster in immer kleinere Cluster aufgeteilt werden, bis jeder Cluster nur noch aus einem Objekt besteht (auch: „Top-down-Verfahren“)
; Divisive Analysis Clustering (DIANA)[6]
Man beginnt mit einem Cluster, das alle Objekte enthält. Im Cluster mit dem größten Durchmesser wird das Objekt gesucht, das die größte mittlere Distanz oder Unähnlichkeit zu den anderen Objekten des Clusters aufweist. Dies ist der Kern des Splitterclusters. Iterativ wird jedes Objekt, das nahe genug am Splittercluster ist, diesem hinzugefügt. Der gesamte Prozess wird wiederholt, bis jeder Cluster nur noch aus einem Objekt besteht.
die agglomerativen Clusterverfahren, in dem zunächst jedes Objekt einen Cluster bildet und dann schrittweise die Cluster in immer größere Cluster zusammengefasst werden, bis alle Objekte zu einem Cluster gehören (auch: „Bottom-up-Verfahren“). Die Verfahren in dieser Familie unterscheiden zum einen nach den verwendeten Distanz- bzw. Ähnlichkeitsmaßen (zwischen Objekten, aber auch zwischen ganzen Clustern) und, meist wichtiger, nach ihrer Fusionsvorschrift, welche Cluster in einem Schritt zusammengefasst werden. Die Fusionierungsmethoden unterscheiden sich in der Art und Weise, wie die Distanz des fusionierten Clusters zu allen anderen Clustern berechnet wird. Wichtige Fusionierungsmethoden sind:
; Single Linkage[7][8][9][10]
Die Cluster, deren nächste Objekte die kleinste Distanz oder Unähnlichkeit haben, werden fusioniert.
; Ward Methode[11]
Die Cluster, die den kleinsten Zuwachs der totalen Varianz haben, werden fusioniert.

Für beide Verfahren gilt: einmal gebildete Cluster können nicht mehr verändert oder einzelne Objekte getauscht werden. Es wird die Struktur entweder stets nur verfeinert („divisiv“) oder nur verallgemeinert („agglomerativ“), so dass eine strikte Cluster-Hierarchie entsteht. An der entstandenen Hierarchie kann man nicht mehr erkennen, wie sie berechnet wurde.

Dichtebasierte Verfahren

Beispiele für dichtebasiertes Clustering

Dichte-basiertes clustering mit DBSCAN.

Da DBSCAN nur einen Dichte-Schwellwert verwendet, kann es benachbarte Cluster nicht immer gut trennen.

OPTICS ist eine DBSCAN-Variante, die besser mit Dichtevariationen umgehen kann.

Bei dichtebasiertem Clustering werden Cluster als Objekte in einem d-dimensionalen Raum betrachtet, welche dicht beieinander liegen, getrennt durch Gebiete mit geringerer Dichte.

DBSCAN[12] (Density-Based Spatial Clustering of Applications with Noise)

Objekte, die in einem vorgegebenen Abstand

\epsilon

mindestens

k

weitere Objekte haben, sind Kernobjekte. Zwei Kernobjekte, deren Distanz kleiner als

\epsilon

ist, gehören dabei zum selben Cluster. Nicht-Kern-Objekte, die nahe einem Cluster liegen, werden diesem als Randobjekte hinzugefügt. Objekte, die weder Kernobjekte noch Randobjekte sind, sind Rauschobjekte.

OPTICS[13] (Ordering Points To Identify the Clustering Structure): Der Algorithmus erweitert DBSCAN, so dass auch verschieden dichte Cluster erkannt werden. Die Wahl des Parameters $\epsilon$ ist nicht mehr so ausschlaggebend um die Clusterstruktur der Objekte zu finden.

Maximum-Margin-Clustering[14]

Es werden (leere) Bereiche im Raum der Objekte gesucht, die zwischen zwei Clustern liegen. Daraus werden Clustergrenzen bestimmt und damit auch die Cluster. Die Technik ist eng angebunden an Support-Vektor-Maschinen.

Gitterbasierte Verfahren

Bei gitterbasierten Clusterverfahren wird der Datenraum unabhängig von den Daten in endlich viele Zellen aufgeteilt. Der größte Vorteil dieses Ansatzes ist die geringe asymptotische Komplexität im niedrigdimensionalen, da die Laufzeit von der Anzahl der Gitterzellen abhängt. Mit steigender Anzahl der Dimensionen wächst jedoch die Zahl der Gitterzellen exponentiell. Vertreter sind STING und CLIQUE. Zudem können Gitter zur Beschleunigung anderer Algorithmen eingesetzt werden, bspw. zur Approximation von k-means oder zur Berechnung von DBSCAN (GriDBSCAN).

Der Algorithmus STING[15] (STatistical INformation Grid-based Clustering) teilt den Datenraum rekursiv in rechteckige Zellen. Statistische Informationen für jede Zelle werden auf der untersten Rekursionsebene vorausberechnet. Relevante Zellen werden anschließend mit einem Top-Down Ansatz berechnet und zurückgegeben.
CLIQUE[16] (CLustering In QUEst) arbeitet in zwei Phasen: Zunächst wird der Datenraum in dicht besetzte d-dimensionale Zellen partitioniert. Die zweite Phase bestimmt aus diesen Zellen größere Cluster, indem durch eine Greedy-Stategie größtmögliche Regionen dicht besetzter Zellen ermittelt werden.

Kombinierte Verfahren

In der Praxis werden oft auch Kombinationen von Verfahren benutzt. Ein Beispiel ist es erst eine hierarchische Clusteranalyse durchzuführen, um eine geeignete Clusterzahl zu bestimmen, und danach noch ein k-Means Clustering, um das Resultat des Clusterings zu verbessern. Oft lässt sich in speziellen Situation zusätzliche Information ausnutzen, so dass z. B. die Dimension oder die Anzahl der zu clusternden Objekte reduziert wird.

Spektrales Clustering[17][18]: Die zu clusterenden Objekte können auch als Knoten eines Graphs aufgefasst werden und die gewichteten Kanten geben Distanz oder Unähnlichkeit wieder. Die Laplace-Matrix, eine spezielle Transformierte der Adjazenzmatrix (Matrix der Ähnlichkeit zwischen allen $n$ Objekten), hat bei $k$ Zusammenhangskomponenten (Clustern) den Eigenwert Null mit der Vielfachheit $k$ . Daher untersucht man die $k$ kleinsten Eigenwerte der Laplace-Matrix und den zugehörigen $k$ -dimensionalen Eigenraum ( $k\ll n$ ). Statt in einem hochdimensionalen Raum wird nun in dem niedrigdimensionalen Eigenraum, z. B. mit dem k-Means-Verfahren, geclustert.
Multiview-Clustering[19]: Hierbei wird davon ausgegangen, dass man mehrere Distanz- oder Ähnlichkeitsmatrizen (sog. views) der Objekte generieren kann. Ein Beispiel sind Webseiten als zu clusternde Objekte: eine Distanzmatrix kann auf Basis der gemeinsam verwendeten Worte berechnet werden, eine zweite Distanzmatrix auf Basis der Verlinkung. Dann wird ein Clustering (oder ein Clustering-Schritt) mit der einen Distanzmatrix durchgeführt und das Ergebnis als Input für ein Clustering (oder ein Clustering-Schritt) mit der anderen Distanzmatrix benutzt. Dies wird wiederholt, bis sich die Clusterzugehörigkeit der Objekte stabilisiert.
Balanced iterative reducing and clustering using hierarchies (BIRCH): Für (sehr) große Datensätze wird zunächst ein Preclustering durchgeführt. Die so gewonnenen Cluster (nicht mehr die Objekte) werden dann z. B. mit einer hierarchischen Clusteranalyse weitergeclustert. Dies ist die Basis des eigens für SPSS entwickelten und dort eingesetzten Two-Step clusterings.

Biclustering

Biclustering, Co-Clustering oder Two-Mode Clustering ist eine Technik, die das gleichzeitige Clustering von Zeilen und Spalten einer Matrix ermöglicht. Zahlreiche Biclustering-Algorithmen wurden für die Bioinformatik entwickelt, darunter: Block Clustering, CTWC (Coupled Two-Way Clustering), ITWC (Interrelated Two-Way Clustering), δ-Bicluster, δ-pCluster, δ-Pattern, FLOC, OPC, Plaid Model, OPSMs (Order-preserving Submatrices), Gibbs, SAMBA (Statistical-Algorithmic Method for Bicluster Analysis), Robust Biclustering Algorithm (RoBA), Crossing Minimization, cMonkey, PRMs, DCC, LEB (Localize and Extract Biclusters), QUBIC (QUalitative BIClustering), BCCA (Bi-Correlation Clustering Algorithm) und FABIA (Factor Analysis for Bicluster Acquisition). Auch in anderen Anwendungsgebieten werden Biclustering-Algorithmen vorgeschlagen und eingesetzt. Dort sind sie unter den Bezeichnungen Co-Clustering, Bidimensional Clustering sowie Subspace Clustering zu finden.

Evaluation

Die Ergebnisse eines jeden Cluster-Verfahrens müssen wie bei allen Verfahren des maschinellen Lernens einer Evaluation unterzogen werden. Die Güte einer fertig berechneten Einteilung der Datenpunkte in Gruppen kann anhand verschiedener Metriken eingeschätzt werden. Die Auswahl einer geeigneten Metrik muss immer im Hinblick auf die verwendeten Daten, die vorgegebene Fragestellung sowie die gewählte Clustering-Methode erfolgen.

Zu den in der Praxis häufig verwendeten Evaluations-Kennzahlen gehört der 1987 von Peter J.Rousseeuw vorgestellte Silhouettenkoeffizient. Dieser berechnet pro Datenpunkt einen Wert, der angibt wie gut die Zuordnung zur gewählten Gruppe im Vergleich zu allen deren Gruppen erfolgt ist.[20] Mit einer Laufzeitkomplexität von O(n²) ist der Silhouettenkoeffizient aber langsamer als viele Clusterverfahren, und kann so nicht auf großen Daten verwendet werden.

Der Silhouettenkoeffizient ist dabei ein Verfahren, welches ohne externe Informationen zur Evaluation auskommt. Diese internen Validitätsmetriken haben den Vorteil, dass kein Wissen über die korrekte Zuordnung vorhanden sein muss, um das Ergebnis zu bewerten. Neben internen Kennzahlen wird in der Wissenschaft zwischen externen und relativen Metriken unterschieden.[21]

Literatur

Grundlagen und Verfahren

Martin Ester, Jörg Sander: Knowledge Discovery in Databases. Techniken und Anwendungen. Springer, Berlin 2000, ISBN 3-540-67328-8.
K. Backhaus, B. Erichson, W. Plinke, R. Weiber: Multivariate Analysemethoden. Eine anwendungsorientierte Einführung. Springer, 2003, ISBN 3-540-00491-2.
S. Bickel, T. Scheffer: Multi-View Clustering. In: Proceedings of the IEEE International Conference on Data Mining. 2004
J. Shi, J. Malik: Normalized Cuts and Image Segmentation. In: Proc. of IEEE Conf. on Comp. Vision and Pattern Recognition. Puerto Rico 1997.
Otto Schlosser: Einführung in die sozialwissenschaftliche Zusammenhangsanalyse. Rowohlt, Reinbek bei Hamburg 1976, ISBN 3-499-21089-4.

Anwendung

J. Bacher, A. Pöge, K. Wenzig: Clusteranalyse – Anwendungsorientierte Einführung in Klassifikationsverfahren. 3. Auflage. Oldenbourg, München 2010, ISBN 978-3-486-58457-8.
J. Bortz: Statistik für Sozialwissenschaftler. Springer, Berlin 1999, Kap. 16 Clusteranalyse
W. Härdle, L. Simar: Applied Multivariate Statistical Analysis. Springer, New York 2003
C. Homburg, H. Krohmer: Marketingmanagement: Strategie – Instrumente – Umsetzung – Unternehmensführung. 3. Auflage. Gabler, Wiesbaden 2009, Kapitel 8.2.2
H. Moosbrugger, D. Frank: Clusteranalytische Methoden in der Persönlichkeitsforschung. Eine anwendungsorientierte Einführung in taxometrische Klassifikationsverfahren. Huber, Bern 1992, ISBN 3-456-82320-7.

Einzelnachweise

vgl. unter anderem Otto Schlosser: Einführung in die sozialwissenschaftliche Zusammenhangsanalyse. Rowohlt, Reinbek bei Hamburg 1976, ISBN 3-499-21089-4.
D. Arthur, S. Vassilvitskii: k-means++: The advantages of careful seeding. In: Proceedings of the eighteenth annual ACM-SIAM Symposium on Discrete algorithms. Society for Industrial and Applied Mathematics, 2007, S. 1027–1035.
S. Vinod: Integer programming and the theory of grouping. In: Journal of the American Statistical Association. Band 64, 1969, S. 506–517, doi:10.1080/01621459.1969.10500990, JSTOR:2283635.
J.C. Bezdek: Pattern recognition with fuzzy objective function algorithms. Plenum Press, New York 1981.
A. P. Dempster, N. M. Laird, D. B. Rubin: Maximum Likelihood from Incomplete Data via the EM algorithm. In: Journal of the Royal Statistical Society. Series B, 39(1), 1977, S. 1–38, doi:10.1111/j.2517-6161.1977.tb01600.x.
L. Kaufman, P. J. Roussew: Finding Groups in Data – An Introduction to Cluster Analysis. John Wiley & Sons 1990.
K. Florek, J. Łukasiewicz, J. Perkal, H. Steinhaus, S. Zubrzycki: Taksonomia wrocławska. In: Przegląd Antropol. 17, 1951, S. 193–211.
K. Florek, J. Łukaszewicz, J. Perkal, H. Steinhaus, S. Zubrzycki: Sur la liaison et la division des points d'un ensemble fini. In: Colloquium Mathematicae. Vol. 2, No. 3–4, Institute of Mathematics Polish Academy of Sciences 1951, S. 282–285.
L. L. McQuitty: Elementary linkage analysis for isolating orthogonal and oblique types and typal relevancies. In: Educational and Psychological Measurement. 1957, S. 207–229, doi:10.1177/001316445701700204.
P. H. Sneath: The application of computers to taxonomy. In: Journal of General Microbiology. 17(1), 1957, S. 201–226, doi:10.1099/00221287-17-1-201.
J. H. Ward Jr: Hierarchical grouping to optimize an objective function In: Journal of the American Statistical Association,. 58(301), 1963, S. 236–244, doi:10.1080/01621459.1963.10500845 JSTOR 2282967.
M. Ester, H. P. Kriegel, J. Sander, X. Xu: A density-based algorithm for discovering clusters in large spatial databases with noise. In: KDD-96 Proceedings. Vol. 96, 1996, S. 226–231.
Mihael Ankerst, Markus M. Breunig, Hans-Peter Kriegel, Jörg Sander: OPTICS: Ordering Points To Identify the Clustering Structure. In: ACM SIGMOD international conference on Management of data. ACM Press, 1999, S. 49–60 (CiteSeerX).
L. Xu, J. Neufeld, B. Larson, D. Schuurmans: Maximum margin clustering. In: Advances in neural information processing systems. 2004, S. 1537–1544.
STING | Proceedings of the 23rd International Conference on Very Large Data Bases. Abgerufen am 6. Juli 2020 (englisch).
Automatic subspace clustering of high dimensional data for data mining applications | Proceedings of the 1998 ACM SIGMOD international conference on Management of data. Abgerufen am 6. Juli 2020 (englisch).
W. E. Donath, A. J. Hoffman: Lower bounds for the partitioning of graphs In: IBM Journal of Research and Development. 17(5), 1973, S. 420–425, doi:10.1147/rd.175.0420.
M. Fiedler: Algebraic connectivity of graphs. In: Czechoslovak Mathematical Journal,. 23(2), 1973, S. 298–305.
S. Bickel, T. Scheffer: Multi-View Clustering. In: ICDM. Vol. 4, Nov 2004, S. 19–26, doi:10.1109/ICDM.2004.10095.
Peter J.Rousseeuw: Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. In: Journal of Computational and Applied Mathematics. Band 20. Elsevier, November 1987, S. 53–65, doi:10.1016/0377-0427(87)90125-7.
Zaki, Mohammed J.; Meira, Wagner.: Data mining and analysis: fundamental concepts and algorithms. Cambridge University Press, 2014, ISBN 978-0-511-81011-4, S. 425 ff.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[schlosser-1] vgl. unter anderem Otto Schlosser: Einführung in die sozialwissenschaftliche Zusammenhangsanalyse. Rowohlt, Reinbek bei Hamburg 1976, ISBN 3-499-21089-4.

[2] D. Arthur, S. Vassilvitskii: k-means++: The advantages of careful seeding. In: Proceedings of the eighteenth annual ACM-SIAM Symposium on Discrete algorithms. Society for Industrial and Applied Mathematics, 2007, S. 1027–1035.

[3] S. Vinod: Integer programming and the theory of grouping. In: Journal of the American Statistical Association. Band 64, 1969, S. 506–517, doi:10.1080/01621459.1969.10500990, JSTOR:2283635.

[4] J.C. Bezdek: Pattern recognition with fuzzy objective function algorithms. Plenum Press, New York 1981.

[5] A. P. Dempster, N. M. Laird, D. B. Rubin: Maximum Likelihood from Incomplete Data via the EM algorithm. In: Journal of the Royal Statistical Society. Series B, 39(1), 1977, S. 1–38, doi:10.1111/j.2517-6161.1977.tb01600.x.

[6] L. Kaufman, P. J. Roussew: Finding Groups in Data – An Introduction to Cluster Analysis. John Wiley & Sons 1990.

[7] K. Florek, J. Łukasiewicz, J. Perkal, H. Steinhaus, S. Zubrzycki: Taksonomia wrocławska. In: Przegląd Antropol. 17, 1951, S. 193–211.

[8] K. Florek, J. Łukaszewicz, J. Perkal, H. Steinhaus, S. Zubrzycki: Sur la liaison et la division des points d'un ensemble fini. In: Colloquium Mathematicae. Vol. 2, No. 3–4, Institute of Mathematics Polish Academy of Sciences 1951, S. 282–285.

[9] L. L. McQuitty: Elementary linkage analysis for isolating orthogonal and oblique types and typal relevancies. In: Educational and Psychological Measurement. 1957, S. 207–229, doi:10.1177/001316445701700204.

[10] P. H. Sneath: The application of computers to taxonomy. In: Journal of General Microbiology. 17(1), 1957, S. 201–226, doi:10.1099/00221287-17-1-201.

[11] J. H. Ward Jr: Hierarchical grouping to optimize an objective function In: Journal of the American Statistical Association,. 58(301), 1963, S. 236–244, doi:10.1080/01621459.1963.10500845 JSTOR 2282967.

[12] M. Ester, H. P. Kriegel, J. Sander, X. Xu: A density-based algorithm for discovering clusters in large spatial databases with noise. In: KDD-96 Proceedings. Vol. 96, 1996, S. 226–231.

[13] Mihael Ankerst, Markus M. Breunig, Hans-Peter Kriegel, Jörg Sander: OPTICS: Ordering Points To Identify the Clustering Structure. In: ACM SIGMOD international conference on Management of data. ACM Press, 1999, S. 49–60 (CiteSeerX).

[14] L. Xu, J. Neufeld, B. Larson, D. Schuurmans: Maximum margin clustering. In: Advances in neural information processing systems. 2004, S. 1537–1544.

[15] STING | Proceedings of the 23rd International Conference on Very Large Data Bases. Abgerufen am 6. Juli 2020 (englisch).

[16] Automatic subspace clustering of high dimensional data for data mining applications | Proceedings of the 1998 ACM SIGMOD international conference on Management of data. Abgerufen am 6. Juli 2020 (englisch).

[17] W. E. Donath, A. J. Hoffman: Lower bounds for the partitioning of graphs In: IBM Journal of Research and Development. 17(5), 1973, S. 420–425, doi:10.1147/rd.175.0420.

[18] M. Fiedler: Algebraic connectivity of graphs. In: Czechoslovak Mathematical Journal,. 23(2), 1973, S. 298–305.

[19] S. Bickel, T. Scheffer: Multi-View Clustering. In: ICDM. Vol. 4, Nov 2004, S. 19–26, doi:10.1109/ICDM.2004.10095.

[20] Peter J.Rousseeuw: Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. In: Journal of Computational and Applied Mathematics. Band 20. Elsevier, November 1987, S. 53–65, doi:10.1016/0377-0427(87)90125-7.

[21] Zaki, Mohammed J.; Meira, Wagner.: Data mining and analysis: fundamental concepts and algorithms. Cambridge University Press, 2014, ISBN 978-0-511-81011-4, S. 425 ff.