Fluggeschwindigkeit

Die Fluggeschwindigkeit ist die Geschwindigkeit eines Luftfahrzeuges.

Fahrtmesser in einem Cockpit

Anzeige auf dem PFD eines modernen Verkehrsflugzeuges. Auf dem linken Streifen wird die Eigengeschwindigkeit in Knoten, darunter die Machzahl angezeigt.

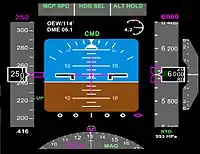
Bei der Messung und Angabe einer Fluggeschwindigkeit (siehe Fahrtmesser) müssen zwei wichtige Bezugssysteme unterschieden werden:

Geschwindigkeit relativ zur Luft (Fahrt, Airspeed): Durch Geschwindigkeit eines Luftfahrzeuges relativ zur Luft entsteht die Luftströmung an Steuer- und Tragflächen. Sie entscheidet daher über das aerodynamische Verhalten des Luftfahrzeugs (Auftriebserzeugung und Manövrierfähigkeit). Sie wird an der Außenseite des Luftfahrzeugs gemessen und auf dem Fahrtmesser im Cockpit angezeigt. Die Airspeed ist die aerodynamisch wichtige Geschwindigkeit. Ihre Messung unterliegt einigen Störeinflüssen, je nach Korrekturgrad werden mehrere „Arten“ der Airspeed unterschieden.
Geschwindigkeit relativ zum Boden (Groundspeed): Die Geschwindigkeit eines Luftfahrzeuges relativ zum Boden entscheidet darüber, wann einzelne Wegpunkte der Flugstrecke und letztlich das Flugziel erreicht werden. Von der Airspeed unterscheidet sie sich vor allem um den Windeinfluss. Sie kann aus der Airspeed errechnet oder auch über ein Navigationssystem ermittelt werden. Die Groundspeed ist die navigatorisch wichtige Geschwindigkeit. Sie kann bei starkem Rückenwind erheblich höher und bei starkem Gegenwind erheblich niedriger liegen als die Airspeed.

Geschwindigkeit relativ zur Luft (Fahrt, Airspeed)

Messverfahren

Pitotrohr an der Unterseite der Tragfläche eines Kleinflugzeuges, das im Bild linke Ende wird im Flug angeströmt

Gemessen wird die Geschwindigkeit mit dem Pitotrohr, im deutschen Sprachgebiet eigentlich Prandtlsonde oder Prandtl’sches Staurohr genannt. Es misst direkt den Druckunterschied zwischen dem statischen Druck der Luft, die das Flugzeug umströmt, und dem Gesamtdruck aus statischem Druck und dynamischem Druck bzw. Staudruck. Aus diesem Druckunterschied wird die angezeigte Fluggeschwindigkeit (IAS) abgeleitet.

Prinzipiell ist die Messung mit dem Pitotrohr in genau gleichem Maße von der (nach oben abnehmenden) Luftdichte abhängig wie auch der Auftrieb an den Tragflächen, so dass der Einfluss der Luftdichte automatisch berücksichtigt wird. Damit bietet das Messverfahren eine gute Grundlage für die Beurteilung der Flugleistung.

In den Anfängen der Fliegerei wurde bei langsamen Flugzeugen versucht, ein Flügelrad zur Messung der Geschwindigkeit zu verwenden.

Die Messung durch das Pitotrohr enthält noch eine Reihe von Störeinflüssen. Daher werden mehrere Korrekturstufen vorgenommen. Manche dieser Störeinflüsse treten erst bei großen Geschwindigkeiten oder großen Flughöhen nennenswert in Erscheinung, können in der Hobbyfliegerei deshalb vernachlässigt werden, sind für die Verkehrsfliegerei jedoch wichtig.

Die Zwischenergebnisse der jeweiligen Korrekturstufen tragen jeweils eine eigene Bezeichnung:

Unkorrigierte Eigengeschwindigkeit (IAS)

Die Unkorrigierte Eigengeschwindigkeit (auch Gerätegeschwindigkeit oder Angezeigte Fluggeschwindigkeit; engl. indicated airspeed, IAS) ist die Geschwindigkeit eines Flugzeugs relativ zur umgebenden Luftmasse, die sich direkt aus der gemessenen Druckdifferenz ergeben würde.

Die IAS hat nur für Kleinflugzeuge Bedeutung, da bei größeren Flugzeugen direkt die CAS angezeigt wird.

Die IAS ist proportional zur Quadratwurzel aus dem Quotienten von dynamischem Druck (Gesamtdruck minus statischer Druck) und Luftdichte. In großer Höhe ist also die IAS bei gleicher Geschwindigkeit relativ zur Luft kleiner. Da alle auf das Flugzeug wirkenden Luftkräfte (Auftrieb und Widerstand) ebenfalls von der Luftdichte abhängig sind, haben die charakteristischen Geschwindigkeiten (Überziehgeschwindigkeit V₀, Manövergeschwindigkeit V_A) konstante IAS-Werte, unabhängig von Flughöhe und Luftdruck. Die zulässige Höchstgeschwindigkeit V_NE dagegen sinkt mit der Höhe, da sie meist vom Flattern bedingt ist, welches mit abnehmender Dämpfung durch die Luft stärker wird.

Berichtigte Fluggeschwindigkeit (CAS)

Bei der Berichtigten Fluggeschwindigkeit (engl. calibrated airspeed, CAS) sind die sogenannten statischen Fehler korrigiert, jedoch noch nicht die dynamischen Fehler.

Die Luftverdrängung durch den Flugzeugrumpf erzeugt eine Druckwelle, ähnlich der Bugwelle eines Schiffes. Diese Druckwelle führt zu einer Verfälschung des Messergebnisses, die vom Flugzeugmuster und vom Einbauort des Pitotrohres abhängt. Man spricht hier auch vom Instrumenten- und Einbaufehler (engl. static source error).

Sofern die Messskala nicht für das spezielle Flugzeugmuster kalibriert wurde, wird der angezeigte Wert anhand einer Tabelle oder einer im technischen Handbuch eines Flugzeugmusters angegebenen Rechenformel korrigiert. Bei Kleinflugzeugen und ihren geringen Geschwindigkeiten bleibt der Fehler üblicherweise so unbedeutend, dass er vernachlässigt werden kann.

Äquivalente Fluggeschwindigkeit (EAS)

Die Äquivalente Fluggeschwindigkeit (engl. equivalent airspeed, EAS) korrigiert zusätzlich den Fehler aufgrund der Kompressibilität der Luft.

Mit zunehmender Geschwindigkeit nimmt ein weiterer Staurohr-Messfehler erheblich zu: Die Kompression der Luft.
Dadurch, dass die Luft vor dem Staurohr komprimiert wird, sieht das Staurohr eine höhere Luftdichte, als sie tatsächlich ist. Da der Fehler mit der Geschwindigkeit zunächst nur langsam zunimmt, variieren die Angaben, ab welcher Geschwindigkeit der Fehler berücksichtigt werden muss, erheblich, im Bereich von 100 bis über 250 Knoten.

Für Start und Landung spielt diese Korrektur eine eher geringe Rolle, da die Geschwindigkeiten dabei geringer sind.

Bei mittleren bis höheren Geschwindigkeiten ist diese Geschwindigkeit aber von wesentlicher Bedeutung, da von ihr die Luftkräfte am Flugzeug abhängen (wichtig für eine stabile Fluglage). Man könnte sagen: Die EAS ist die Geschwindigkeit, die das Flugzeug „fühlt“.

Allerdings: Nähert sich die Geschwindigkeit der Schallgeschwindigkeit, tritt stattdessen die Machzahl in den Vordergrund. (siehe Abschnitt unten)

Die Äquivalente Geschwindigkeit ist eine fiktive Geschwindigkeit, die über die aerodynamischen Verhältnisse Auskunft gibt. Bei gleicher Äquivalenter Geschwindigkeit erzeugt ein Luftfahrzeug stets denselben Auftrieb, unabhängig von der Dichte der umgebenden Luft. In Meereshöhe in der Standardatmosphäre entspricht die Äquivalente Geschwindigkeit der Wahren Geschwindigkeit. Je dünner die Luft ist, umso höher muss die Wahre Geschwindigkeit (TAS) sein, um die gleiche Äquivalente Geschwindigkeit, also die gleiche aerodynamische Wirkung zu erreichen. Die Äquivalente Geschwindigkeit lässt aber nicht nur Aussagen über den Auftrieb zu, sondern genauso auch über andere Kräfte und Größen, beispielsweise Kräfte, die auf die Lande- und Steuerklappen wirken, oder wie viel Reibungshitze erzeugt wird und ähnliches.

Für Kleinflugzeuge stimmt die EAS wegen der geringen Geschwindigkeiten und Flughöhen noch in ausreichender Näherung mit CAS oder sogar IAS überein und muss nicht eigens ermittelt werden.

Wahre Fluggeschwindigkeit (TAS)

Die Wahre Fluggeschwindigkeit (engl. true airspeed, TAS) ist die tatsächliche Geschwindigkeit eines Luftfahrzeuges relativ zur umgebenden Luft. In der Standardatmosphäre in Meereshöhe und unterhalb 100 Knoten sind TAS und IAS fast gleich. Nimmt die Luftdichte ab (mit steigender Flughöhe oder Temperatur) oder die Fahrt zu (steigende Kompression), so ist die IAS niedriger als die TAS.

Die Berechnung der TAS erfolgt aus der EAS, indem auch noch die Luftdichte in die Berechnung einbezogen wird. Sie lässt sich aus Luftdruck und Temperatur abschätzen und sagt aus, wie viel „Angriffsmasse“ einer Tragfläche zur Verfügung steht und wie viel Masse gegen die Sensoren im Pitot-System strömt. Die Dichte der Luft darf dabei nicht mit ihrem Druck verwechselt werden: Wärmere Luft hat bei gleichem Druck eine geringere Dichte als kältere.

Für Verkehrsflugzeuge, die von Startbahn bis Gipfelhöhe einen großen Bereich unterschiedlicher Luftdichten und Geschwindigkeiten überstreichen, ist diese Korrektur sehr komplex zu berechnen, da zusätzlich berücksichtigt werden muss, dass durch die Kompression der Luft diese sich auch erwärmt. Die gemessenen Temperaturen müssen entsprechend korrigiert werden.

Praktisch wird die TAS aus der CAS errechnet, so dass zwei Rechenschritte zusammengefasst werden (CAS → EAS → TAS). Für hohe Geschwindigkeiten ist die Berechnung recht aufwändig. Sofern die Berechnung der TAS nicht durch eine computerunterstützte Anzeige erfolgt, kann man sie in einer iterativen Berechnung mit Hilfe eines Flight Calculators vornehmen (Rechenscheibe ähnlich einem Rechenschieber, mit zusätzlichen Hilfsskalen und Tabellen).

Für Kleinflugzeuge und ihren Einsatzbereich können wiederum vereinfachte Formeln herangezogen werden bzw. vereinfachte Anzeigeinstrumente eingesetzt werden, bei denen zum Beispiel die TAS ermittelt wird, indem der Skalenring verdreht wird und dabei die sogenannte Druckhöhe mit der Außentemperatur zur Deckung gebracht wird (siehe Abbildung von einem Fahrtmesser ganz oben). Für große Flughöhen und hohe Geschwindigkeiten dagegen wären solche Instrumente völlig ungeeignet.

Für Piloten von Kleinflugzeugen gilt in erster Näherung folgende Faustformel:

In Kleinflugzeugen ist die TAS um ca. 2 Prozent pro 1000 ft AMSL Flughöhe höher als die CAS bzw. IAS.

Beispielsweise ist in einer Flughöhe von 5000 ft bei einer IAS-Anzeige von 100 kt und einer ähnlichen CAS die TAS 5 * 2 % = 10 % höher, also 110 kt TAS.

Formel

Im Prinzip gilt die folgende Abhängigkeit:

V_{\mathrm {TAS} }=V_{\mathrm {EAS} }\cdot {\sqrt {\frac {\rho _{\mathrm {INA} }}{\rho _{\mathrm {real} }}}}

mit:

$\rho _{\mathrm {INA} }=1{,}225\,{\frac {\mathrm {kg} }{\mathrm {m^{3}} }}$	: Luftdichte der ICAO-Standardatmosphäre
$\rho _{\mathrm {real} }$	: Luftdichte in gegenwärtiger Höhe

Allerdings hilft diese Formel in der Praxis nur bedingt weiter, da die Luftdichte nicht direkt gemessen werden kann, sondern aus Luftdruck und Temperatur abgeschätzt werden muss.

Mach-Zahl

Für die Luftfahrt spezialisierte Rechenscheibe. (Z.B. für die Umrechnung von Indicated Airspeed zu True Airspeed oder Indicated Airspeed zu Mach-Zahl)

Die Mach-Zahl ist das Verhältnis der TAS zur Schallgeschwindigkeit bei gegenwärtiger Lufttemperatur.

Bei hohen Geschwindigkeiten wird statt der TAS häufig die Mach-Zahl angegeben. Das hat seinen Grund darin, dass insbesondere in den Bereichen Flugzeugnase und auf der Oberseite der Tragflächen (insbesondere an der Tragflächenvorderkante und dem Übergang von der Tragfläche in den Rumpf) Strömungsgeschwindigkeiten auftreten, die deutlich über der Fluggeschwindigkeit liegen. Folglich treten also schon deutlich unterhalb der Schallgeschwindigkeit am Flugzeug Strömungsgeschwindigkeiten im Überschallbereich auf. Da die Belastungen im Bereich der Schallgeschwindigkeit fast sprunghaft zunehmen, ist die Höchstgeschwindigkeit keine absolute Größe, sondern ein Verhältnis zur Schallgeschwindigkeit. Da die Schallgeschwindigkeit mit sinkenden Temperaturen abnimmt, nimmt auch die Höchstgeschwindigkeit (TAS) mit der Temperatur ab, so dass die Mach-Zahl angibt, wie stark man sich der Höchstgeschwindigkeit annähert. Auch die Mach-Zahl ist also ungeeignet für die Flugplanung, sondern dient der aerodynamischen Steuerung. Insbesondere ist bei schnell fliegenden Flugzeugen ab etwa Mach 0,75 die Höchstgeschwindigkeit nicht durch die Äquivalente Fluggeschwindigkeit bestimmt, sondern stattdessen durch die Mach-Zahl.

Geschwindigkeit relativ zum Boden (Groundspeed)

Die Geschwindigkeit über Grund (engl. ground speed, GS) bezeichnet die um den Windeinfluss (also die Bewegung der durchflogenen Luftmasse selbst) korrigierte Wahre Fluggeschwindigkeit. Sie stellt die Geschwindigkeit eines Luftfahrzeuges relativ zur Erdoberfläche dar. Die Kenntnis der ground speed ist zur Flugplanung wichtig. Nur sie sagt aus, wann einzelne Wegpunkte oder das Flugziel erreicht werden. Vor allem bei Gegen- oder Rückenwind kann sich die Geschwindigkeit über Grund ganz erheblich von der im Cockpit angezeigten Airspeed unterscheiden; bei Rückenwind entspricht die Groundspeed der Summe aus Airspeed und Windgeschwindigkeit. Deshalb werden Jetstreams in Strömungsrichtung zur Flugzeitverkürzung genutzt.

Unter besonderen Umständen kann eine zu niedrige Groundspeed verbunden mit einer zu hohen Anzeige im Cockpit zu Unfällen, wie dem Absturz der Star Dust über den Anden, führen.

Man kann die Geschwindigkeit über Grund durch Berücksichtigung des Windes mittels Winddreieck auf Grundlage der Meldungen der Flugwetterwarten berechnen, heutzutage aber auch durch moderne Bordsysteme messen (z. B. Trägheitsnavigationssystem, Dopplereffekt, Flugnavigationsfunkdienst).

Unterstützend kommen auch Navigationsverfahren wie beispielsweise GPS in Frage. Allerdings ist die alleinige Navigation nach GPS in der zivilen Luftfahrt nicht zulässig, da es unter militärischer Verantwortung und Kontrolle betrieben wird und von keiner anerkannten Organisation der Zivilluftfahrt. Außerdem ist es bei erhöhter Sonnenaktivität störanfällig. Wegen seiner einfachen Nutz- und Verfügbarkeit spielt es jedoch in der nichtgewerblichen Luftfahrt eine wichtige ergänzende Rolle.

Maßeinheit

Üblicherweise werden in der Luftfahrt alle Fluggeschwindigkeiten in Knoten angegeben (1 Knoten = 1 kn = 1 sm/h = 1,852 km/h[1], denn 1 Seemeile sm = 1,852 km). Ausnahmen bilden Russland und die Staaten der GUS. In Segel- und Ultraleichtflugzeugen wird in Deutschland die Fluggeschwindigkeit, abweichend vom internationalen Standard, in km/h gemessen.

In der internationalen zivilen Luftfahrt wird häufig als Einheit ein K (für Knoten) mit der Art der Geschwindigkeit (IAS/TAS) kombiniert: KIAS (knots indicated airspeed) oder KTAS (knots true airspeed).

Für größere Flughöhen und Geschwindigkeiten ist die Mach-Zahl (das Verhältnis zur Schallgeschwindigkeit) von zusätzlichem Nutzen.

Beispiel

Die verschiedenen Geschwindigkeiten werden in nachfolgender Tabelle verglichen. Man beachte, wie trotz abnehmender IAS die Geschwindigkeit über Grund letztendlich mit zunehmender Höhe steigt.

Flughöhe	IAS	TAS	Wind	GS	Mach	Anmerkung
1000 ft (ca. 300 m)	150 kt (278 km/h)	153 kt (283 km/h)	kein Wind	153 kt (283 km/h)		durchschnittliches Verkehrsflugzeug kurz nach dem Start
FL100 (ca. 3 km)	250 kt (463 km/h)	300 kt (556 km/h)		300 kt (556 km/h)
FL200 (ca. 6 km)	310 kt (574 km/h)	434 kt (803 km/h)		434 kt (803 km/h)
FL360 (ca. 11 km)	280 kt (518 km/h)	480 kt (889 km/h)	20 kt Rückenwind	500 kt (926 km/h)	0,82	Reiseflug, höhere IAS durch Machzahl begrenzt
FL360 (ca. 11 km)	280 kt (518 km/h)	480 kt (889 km/h)	20 kt Gegenwind	460 kt (852 km/h)	0,82	Reiseflug, höhere IAS durch Machzahl begrenzt

Typische Geschwindigkeiten

Bei kleinen Motorflugzeugen liegt die typische Reisegeschwindigkeit bei ca. 110 kt (200 km/h). Diese kann jedoch je nach Typ und Motorisierung stark variieren. Bei Verkehrsflugzeugen mit Turboprop-Antrieb liegt sie bei bis zu 350 kt (650 km/h). Bei Verkehrsflugzeugen mit Strahlantrieb liegt sie bei rund 80 % bis 85 % der Schallgeschwindigkeit, was – je nach Temperatur zwischen FL100 und FL360 – etwa 490 bis 540 kt (ca. 900 bis 1000 km/h) entspricht. Begrenzt wird die Geschwindigkeit durch die Flugzeugstruktur, durch Vorschriften, z. B. unterhalb FL100 (10.000 ft/ 3.048 m Flughöhe höchstens 250 kt) und spätestens auf Reiseflughöhe durch die Mach-Zahl (Annäherung an die „Schallmauer“). Die Eigengeschwindigkeit eines Segelflugzeugs liegt ca. zwischen 30 und 150 kn (≈ 50 – ≈ 270 km/h). Die IAS/CAS/TAS eines Ballons ist hingegen meistens nahezu Null, da er der Luftströmung (abgesehen von Trägheitseffekten) folgt.

Fluggeschwindigkeit und Motorleistung

Für die Fluggeschwindigkeit im Horizontalflug gilt folgende Näherungsformel:

v_{h}={\sqrt[{3}]{\frac {75\cdot N\cdot 2\cdot g\cdot \eta _{L}}{C_{w}\cdot \rho \cdot A}}}

wobei:

$v_{h}$ : Horizontalgeschwindigkeit in m/s
$N$ : Motorleistung in PS
$\eta _{L}$ : Wirkungsgrad Luftschraube
$C_{w}$ : Luftwiderstandsbeiwert Flugzeug
$g$ : Erdbeschleunigung 9,81 m/s²
$\rho$ : Luftdichte in kg/m³
$A$ : Flügelfläche in m²

Z. B. Welche Reisegeschwindigkeit hat ein Kleinmotorflugzeug mit N = 100 PS; η_L = 0,8; ρ = 1,2 kg/m³; C_w = 0,06; A = 15 m² in niedriger Flughöhe?

v_{h}={\sqrt[{3}]{\frac {75\cdot 100\cdot 2\cdot 9{,}81\cdot 0{,}8}{0{,}06\cdot 1{,}2\cdot 15}}}=48\,\mathrm {m/s} =173\,\mathrm {km/h}

Literatur

K. J. Lush: Standardization of Take-Off Performance Measurements for Airplanes, Technical Note R-12. AFFTC, Edwards AFB, California.
John D. Anderson Jr.: Introduction to Flight, 3rd ed. McGraw-Hill Book, New York 1989.
Russel M. Herrington: Flight Test Engineering Handbook. AF Technical Report 6273, AFFTC, Edwards AFB, California 1966
Russell E. Erb: A Low Cost Method for Generating Takeoff Ground Roll Charts from Flight Test Data. Society of Flight Test Engineers (SFTE) 27th Annual Symposium, Fort Worth TX, 196
Privat Pilot Manual. Jeppesen Sanderson, Englewood CO 1997, 2001, ISBN 0-88487-238-6
Peter Dogan: Instrument Flight Training Manual. Aviation Book, Santa Clarita CA 1991, 1999, ISBN 0-916413-12-8.
Rod Machado: Instrument Pilot’s Survival Manual. Aviation Speakers Bureau, Seal Beach CA 1991, 1998, ISBN 0-9631229-0-8.
Wolfgang Kühr: Der Privatflugzeugführer. Bd. 3, Technik II. Schiffmann Verlag, Bergisch Gladbach 1981, 1999, ISBN 3-921270-09-X.
Karl-Albin Kruse: Das große Buch der Fliegerei und Raumfahrt. Südwest-Verlag, München 1973, ISBN 3-517-00420-0.
Klaus Hünecke: Die Technik des modernen Verkehrsflugzeuges. Motorbuchverlag, Stuttgart 1998, ISBN 3-613-01895-0.

Einzelnachweise

DIN EN ISO 80000-3:2013 Größen und Einheiten – Teil 3: Raum und Zeit, Abschnitt 3-8.b

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] DIN EN ISO 80000-3:2013 Größen und Einheiten – Teil 3: Raum und Zeit, Abschnitt 3-8.b