Lichtstrom

Lichtstrom (englisch luminous flux,[1] Formelzeichen $\Phi _{\mathrm {v} }$ ) ist eine photometrische Größe, die angibt, wie viel für das menschliche Auge wahrnehmbares Licht eine Lichtquelle pro Zeiteinheit abstrahlt. Er entspricht der physikalischen (radiometrischen) Strahlungsleistung, berücksichtigt aber zusätzlich die Empfindlichkeit des menschlichen Auges. Er wird in der Maßeinheit Lumen (lm) angegeben.

Physikalische Größe

Name

Lichtstrom

Formelzeichen

$\Phi _{\mathrm {v} },F\$

Größen- und Einheitensystem	Einheit	Dimension
SI	Lumen (lm)	J

Definition

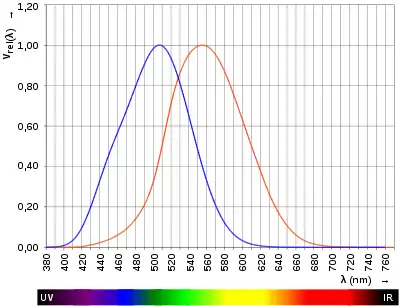
Relative Hellempfindlichkeitskurven für Tagsehen V(λ) (rot) und Nachtsehen V'(λ) (blau)

Jede Lichtquelle gibt Energie in Form von elektromagnetischer Strahlung ab. Die pro Zeiteinheit abgestrahlte Energie wird als Strahlungsleistung oder Strahlungsfluss $\Phi _{\mathrm {e} }$ bezeichnet. Für das menschliche Auge ist aber nur ein begrenzter Spektralbereich zugänglich, und auch im sichtbaren Bereich hängt die Empfindlichkeit des Auges stark von der Wellenlänge $\lambda$ ab. Für die Beschreibung des Helligkeitseindrucks wird der sichtbare Anteil der Strahlungsleistung daher mit der Hellempfindlichkeitskurve des menschlichen Auges bewertet (gewichtet). Das Ergebnis ist der Lichtstrom $\Phi _{\mathrm {v} }$ („v“ für „visuell“ kennzeichnet den Lichtstrom als photometrische Größe).[2] Um zu betonen, dass der Lichtstrom eine speziell auf das menschliche Auge abgestimmte Größe ist, wird er nicht in der Maßeinheit Watt (W) angegeben, sondern hat seine eine eigene Maßeinheit, das Lumen (lm).

Der Umrechnungsfaktor zwischen Strahlungsleistung und Lichtstrom ist das spektrale photometrischen Strahlungsäquivalent

K(\lambda )=K_{\mathrm {m} }\cdot V(\lambda )\ .

Dabei ist V(λ) die Hellempfindlichkeitskurve für Tagsehen. Ihr Maximum V(λ) = 1 liegt bei der Wellenlänge λ = 555 nm (grünes Licht). Der Skalierungsfaktor K_m wurde auf 683 lm/W festgelegt, damit die so definierte Maßeinheit Lumen möglichst gut mit ihrer früheren Definition übereinstimmte.[Anm. 1]

Im Fall von monochromatischem Licht (nur eine Wellenlänge) ist der Lichtstrom

\Phi _{\mathrm {v} }=K(\lambda )\cdot \Phi _{\mathrm {e} }=K_{\mathrm {m} }\cdot V(\lambda )\cdot \Phi _{\mathrm {e} }\ .

Für monochromatisches Licht der Wellenlänge λ = 555 nm entspricht also eine Strahlungsleistung von 1 W einem Lichtstrom von 683 lm, bei anderen Wellenlängen ist der Lichtstrom bei gleicher Strahlungsleistung geringer.

Im Regelfall besteht Licht aber aus einem Gemisch von Wellenlängen. Dann muss die spektrale Strahlungsleistung $\textstyle {\mathrm {d} \Phi _{\mathrm {e} }(\lambda )}/{\mathrm {d} \lambda }$ für jede Wellenlänge mit dem entsprechenden spektralen photometrischen Strahlungsäquivalent multipliziert werden, d. h. man berechnet das Integral über die Wellenlänge:[1]

\Phi _{\mathrm {v} }=K_{\mathrm {m} }\int V(\lambda )\ {\frac {\mathrm {d} \Phi _{\mathrm {e} }(\lambda )}{\mathrm {d} \lambda }}\ \mathrm {d} \lambda \ .

Bei geringer Helligkeit (genauer: Leuchtdichte), dem so genannten Nachtsehen, wird das Licht im Auge von anderen Zellen registriert, die eine andere Empfindlichkeit aufweisen. Die entsprechenden Größen sind dann K′_m = 1700 lm/W und V′(λ). V′(λ) hat sein Maximum bei λ = 507 nm.[3]

Auf analoge Weise können auch andere photometrische Größen (Lichtstärke, Beleuchtungsstärke, Leuchtdichte, …) messtechnisch oder rechnerisch direkt aus der entsprechenden radiometrischen Größe (Strahlstärke, Bestrahlungsstärke, Strahldichte, …) abgeleitet werden, wenn bekannt ist, aus welchem Wellenlängengemisch sich die betreffende elektromagnetische Strahlung zusammensetzt.

Der auf diese Weise ermittelte sichtbare Anteil der elektromagnetischen Strahlung („Licht“ im photometrischen Sinne) stellt ein quantitatives Maß für den Lichtreiz dar, der im Auge eine Helligkeitsempfindung hervorruft. Die subjektive Wahrnehmung dieser Helligkeitsempfindung mit ihren Anpassungs-, Kontrast- und sonstigen wahrnehmungsphysiologischen Effekten ist nicht mehr Thema der Photometrie.

Frühere Definition

Photometrische Messungen erfolgten ursprünglich anhand von genormten Lichtquellen („Standardkerzen“), die ein Gemisch von Wellenlängen emittierten. Größen und Einheiten der Photometrie waren von denen der Radiometrie und des übrigen SI getrennt. Als fundamentale photometrische Größe wurde die Lichtstärke (Lichtstrom durch Raumwinkel: ${\textstyle \mathrm {d} \Phi _{\mathrm {v} }/{\mathrm {d} \Omega }}$ ) gewählt, weil der visuelle Vergleich von Lichtquellen im Vordergrund stand und die Lichtstärke diejenige Eigenschaft der Quellen war, die am einfachsten einem Vergleich zugänglich war.[4] Die Einheit der Lichtstärke (seit 1947 die Candela) galt als Basiseinheit. In mathematisch vereinfachter Darstellung lautete die Definition des Lichtstroms (die inhaltlich auch heute noch gilt):[5]

Wenn die Lichtstärke innerhalb eines Raumwinkels konstant ist, dann ist der in diesem Raumwinkel abgestrahlte Lichtstrom das Produkt aus der Lichtstärke und dem Raumwinkel.

1979 wurde die Candela neu definiert, indem das Lumen über das photometrische Strahlungsäquivalent an das Watt angebunden wurde. Da der Lichtstrom nunmehr die fundamentalere Größe war,[6] plädierte das zuständige internationale Gremium im Vorfeld dafür, dass der Lichtstrom die Lichtstärke als Basisgröße und das Lumen die Candela als Basiseinheit ablösen sollte.[7] Der Antrag wurde jedoch verworfen, um die Zustimmung zur Neudefinition der photometrischen Einheiten insgesamt nicht zu gefährden.

Beispiele typischer Lichtströme

Im Folgenden werden beispielhaft die Lichtströme gebräuchlicher Leuchtmittel gelistet.

Die hier tabellierte in lm/W gemessene Lichtausbeute ist nicht zu verwechseln mit dem oben erwähnten, ebenfalls in lm/W gemessenen photometrischen Strahlungsäquivalent. Letzteres beschreibt, wie viele Lumen auf jedes Watt der abgestrahlten elektromagnetischen Leistung entfallen. Die Lichtausbeute beschreibt, wie viele Lumen auf jedes Watt der von der Lichtquelle aufgenommenen (meist elektrischen) Leistung entfallen, schließt also technische Umwandlungsverluste mit ein.

Glühlampen

Typische Werte für Alltagsgebrauchslampen der Hauptreihe 230 V, Lampen mit Doppelwendel:[8]

Leistung W	Lichtstrom lm	Lichtausbeute lm/W
40	430	10,8
60	730	12,2
100	1380	13,8
500	8400	16,8

Typische Werte für Niedervolt-Halogenglühlampen ohne Reflektor, Farbtemperatur 3000 K:[9]

Leistung W	Lichtstrom lm	Lichtausbeute lm/W
10 (12 V)	140	14
20 (12 V)	350	17,5
50 (12 V)	950	19
50 (24 V)	850	17
100 (12 V)	2300	23
100 (24 V)	2200	22

Leuchtstofflampen

Typische Werte für Leuchtstofflampen der Lichtfarbe hellweiß, Bauform Stab (Durchm. 26 mm):[10]

Leistung W	Rohrlänge mm	Lichtstrom lm	Lichtausbeute lm/W	Leuchtdichte cd/m²
15	438	650	43	07000
30	895	1600	53	07500
36	1200	3350	93	11400
58	1500	5200	90	14500

(Leistungsaufnahme ohne Berücksichtigung des Vorschaltgeräts)

Andere Lichtquellen

Glühwürmchen	0,0144 lm[11] pro cm² Leuchtfläche
Anzeige-LED	ca. 0,001 – 1 lm[12]
Kerze	ca. 10 lm[13]
„High-Power“-LED	bis 4250 lm[14] bis 250 lm/W[15][16][12]
Sonne	3,7·10²⁸ lm[17]

Eine umfangreiche Tabelle gibt es in Lichtquelle#Beispiele.

Messverfahren

Ulbrichtsche Kugel (Kugelphotometer)

Die gängige, jedoch relative Messung mit Hilfe einer Ulbrichtschen Kugel führt zu einem vergleichsweise schnellen Ergebnis, welches im Millisekunden-/Sekundenbereich vorliegt. Unter Beachtung der Vorbereitungszeiten, wie kontrolliertes Altern (48 h für Halogenlampen) oder thermisches Stabilisieren (2 h für LED-Leuchten und -Lampen), der Lichtquelle wird der Zeitvorteil jedoch reduziert. Ein an der Ulbrichtkugel angeschlossenes Photometer/Spektrometer erlaubt das sofortige Ablesen des Lichtstroms. Präzise Messungen sind unter drei Voraussetzungen durchführbar:

Die (relativ) messende Kugel muss durch eine geeignete Lichtquelle identischer räumlicher Abstrahlung kalibriert worden sein, da die Lichtdurchmischung bei gängiger Photometerfarbe (Innenauskleidung der Kugel) nicht ausreichend ist. Eine Erhöhung des Reflexionsgrades zu Werten von größer 90 % wird durch die CIE nicht mehr empfohlen, da die Langzeitstabilität durch unumgängliches Einstauben der unteren Kugelhälfte nicht gewährleistet werden kann.
Zweitens muss die Kugel entweder mit einer bekannten Lichtquelle identischer Spektralverteilung kalibriert werden oder das Gesamtsystem „Kugel mit montiertem Photometerkopf“ muss eine spektrale Empfindlichkeit ähnlich zur Hellempfindlichkeitsfunktion des (menschlichen) Auges haben. Dieser Anspruch ist jedoch nur für Photometer (schnell auslesbar) mit Partialfilterung sowie Spektrometer (deutlich langsamer auslesbar) mit integrierter Streulichtmatrix-Korrektur erfüllbar.
Drittens muss die Bauform (Abmessungen, Eigenabsorption) der Kalibrierlichtquelle mit der Bauform des Prüflings übereinstimmen. Eine Zusatzkalibrierung mit sog. Hilfslampe ist oftmals nicht ausreichend, speziell bei hoher Eigenabsorption.

Zusammenfassend lässt sich festhalten, dass die Kugel hervorragende Messergebnisse liefert, wenn „Gleich gegen Gleich“ und somit relativ gemessen wird. Weichen die räumliche oder spektrale Ausstrahlung oder die Bauform der Kalibrierlichtquelle vom Messobjekt ab, so ist die Messunsicherheit erheblich vergrößert.

Aus der Lichtstärkeverteilung (Goniophotometer)

Die weitaus genauere, weil absolute Messung des Lichtstromes wird mit Hilfe eines Photometerkopfes, montiert an einem Goniometer durchgeführt. Das Goniometer bewegt den Photometerkopf (eigentlich Beleuchtungsstärkemesskopf) auf einer virtuellen Kugelfläche um das Messobjekt. Je nach Verteilung der winkelabhängigen Lichtstärke der Lichtquelle liegt die Messdauer im Bereich von Minuten/Stunden. Wichtig ist hierbei, dass die zu vermessende Lichtquelle über die Messdauer stabil arbeitet. Die vom Goniometer gefahrenen Bahnen liegen historisch begründet auf Loxodromen (Spiralbahnen) oder bilden Großkreise/Kleinkreise nach. Ist die Lichtstärkeverteilung (LVK) ansatzweise bekannt, kann per CNC jedes denkbare Raster abgetastet werden und somit der zeitliche Messaufwand erheblich reduziert werden. Liegt nach Beendigung der Messwertaufnahme eine sinnvolle räumliche Verteilung der Messwerte vor, so ist mit Hilfe von numerischen Methoden möglich, den Lichtstrom aus der Lichtstärkeverteilung zu errechnen. Ebenso wie bei der Messung am Kugelphotometer ist die spektrale Anpassung des Messkopfes wichtig, nach DIN 5032 Teil 7 ergibt sich ein Klasse L Messkopf ausschließlich bei einem Gesamtfehler kleiner 1,5 %. Der Einsatz von Beleuchtungsstärkemessköpfen mit Partialfilterung ist notwendig. Weiterhin ist auf ein hinreichend enges Messraster zu achten.

Zusammenhang mit anderen radiometrischen und photometrischen Größen

radiometrische Größe	Symbol^a)	SI-Einheit	Beschreibung	photometrische Entsprechung^b)	Symbol	SI-Einheit
Strahlungsfluss Strahlungsleistung, radiant flux, radiant power	$\Phi _{\mathrm {e} }$	W (Watt)	Strahlungsenergie durch Zeit	Lichtstrom luminous flux	$\Phi _{\mathrm {v} }$	lm (Lumen)
Strahlstärke Strahlungsstärke, radiant intensity	$I_{\mathrm {e} }$	W/sr	Strahlungsfluss durch Raumwinkel	Lichtstärke luminous intensity	$I_{\mathrm {v} }$	cd = lm/sr (Candela)
Bestrahlungsstärke irradiance	$E_{\mathrm {e} }$	W/m²	Strahlungsfluss durch Empfängerfläche	Beleuchtungsstärke illuminance	$E_{\mathrm {v} }$	lx = lm/m² (Lux)
Spezifische Ausstrahlung Ausstrahlungsstromdichte, radiant exitance	$M_{\mathrm {e} }$	W/m²	Strahlungsfluss durch Senderfläche	Spezifische Lichtausstrahlung luminous exitance	$M_{\mathrm {v} }$	lm/m²
Strahldichte Strahlungsdichte, Radianz, radiance	$L_{\mathrm {e} }$	W/m²sr	Strahlstärke durch effektive Senderfläche	Leuchtdichte luminance	$L_{\mathrm {v} }$	cd/m²
Strahlungsenergie Strahlungsmenge, radiant energy	$Q_{\mathrm {e} }$	J (Joule)	durch Strahlung übertragene Energie	Lichtmenge luminous energy	$Q_{\mathrm {v} }$	lm·s
Bestrahlung Einstrahlung, radiant exposure	$H_{\mathrm {e} }$	J/m²	Strahlungsenergie durch Empfängerfläche	Belichtung luminous exposure	$H_{\mathrm {v} }$	lx·s
Strahlungsausbeute radiant efficiency	$\eta _{\mathrm {e} }$	1	Strahlungsfluss durch aufgenommene (meist elektrische) Leistung	Lichtausbeute (overall) luminous efficacy	$\eta _{\mathrm {v} }$	lm/W

^a) Der Index „e“ dient zur Abgrenzung von den photometrischen Größen. Er kann weggelassen werden.

^b) Die photometrischen Größen sind die radiometrischen Größen, gewichtet mit dem photometrischen Strahlungsäquivalent K, das die Empfindlichkeit des menschlichen Auges angibt.

Literatur

Hans R. Ris: Beleuchtungstechnik für Praktiker. 2. Auflage. VDE-Verlag, Berlin/ Offenbach 1997, ISBN 3-8007-2163-5.
Günter Springer: Fachkunde Elektrotechnik. (= Europa-Lehrmittel. 30318). 18., völlig neubearbeitete und erweiterte Auflage. Verlag Europa-Lehrmittel, Wuppertal 1989, ISBN 3-8085-3018-9.
Wilhelm Gerster: Moderne Beleuchtungssysteme für drinnen und draußen. Compact Verlag, München 1997, ISBN 3-8174-2395-0.
Horst Stöcker: Taschenbuch der Physik. 4. Auflage. Verlag Harry Deutsch, Frankfurt am Main 2000, ISBN 3-8171-1628-4.

Weblinks

Fotometrie Applet – Veranschaulichung fotometrischer Größen

Anmerkungen

Die exakte Festlegung ist K_cd = 683 lm/W für Strahlung der Frequenz 540 THz, was in Luft λ = 555,016 nm entspricht. Bei λ = 555 nm hat K seinen maximalen Wert K_m = 683,002 lm/W (Terminologie der IEC)

Einzelnachweise

International Electrotechnical Commission (IEC): International Electrotechnical Vocabulary. ref. 845-21-039, Luminous flux (abgerufen am 26. März 2021).
Ludwig Bergmann, Clemens Schaefer: Optik: Wellen- und Teilchenoptik. In: Bergmann-Schaefer Lehrbuch der Experimentalphysik. Band 3. Walter de Gruyter, 2004, ISBN 3-11-017081-7, S. 637 (eingeschränkte Vorschau in der Google-Buchsuche).
BIPM Rapport BIPM-2019/05 Principles governing photometry, 2nd ed., (PDF, 1,01 KiB) – Bericht des BIPM von 2019, Kap. 6.3
W. R. Blevin, B. Steiner: Redefinition of the Candela and the Lumen. In: Metrologia. 11, 1975, S. 97–104. doi:10.1088/0026-1394/11/3/001
H. A. E. Keitz: Lichtberechnungen und Lichtmessungen. 2. Auflage. Philips Technische Bibliothek, Eindhoven 1967, S. 25.
BIPM Rapport BIPM-2019/05 Principles governing photometry, 2nd ed., (PDF, 1,01 KiB) – Bericht des BIPM von 2019, Kap. 1, S. 3 „Luminous flux is the most fundamental quantity in photometry because it has the simplest relationship with radiant power.“
Comité International des Poids et Mesures – Procès verbaux des séances. 66^e session. 2^e série, 1977, S. 5–6 (bipm.org [PDF]). (7,4 MB): „Recommandation P 3 (lumen comme unité de base avec une définition en fonction du watt) est celle qui a la préférence de la majorité du CCPR.“ Das CCPR (Comité Consultatif de Photométrie et Radiométrie) ist das zuständige Beratungsgremium des Internationalen Komitees für Maß und Gewicht (CIPM). Der Wortlaut der Empfehlung P 3 befindet sich auf Seite 143 desselben Dokuments.
H.-J. Hentschel: Licht und Beleuchtung – Theorie und Praxis der Lichttechnik. 4. Auflage. Hüthig Buch, Heidelberg 1994, ISBN 3-7785-2184-5, S. 128.
H.-J. Hentschel: Licht und Beleuchtung – Theorie und Praxis der Lichttechnik. 4. Auflage. Hüthig Buch, Heidelberg 1994, ISBN 3-7785-2184-5, S. 131.
H.-J. Hentschel: Licht und Beleuchtung – Theorie und Praxis der Lichttechnik. 4. Auflage. Hüthig Buch, Heidelberg 1994, ISBN 3-7785-2184-5, S. 134.
H. E. Ives: The Fire-Fly as an Illuminant. In: Journal of the Franklin Institute. vol. 194, no. 2, August 1922, S. 213–230. doi:10.1016/S0016-0032(22)90057-2, „on specimens of the larva of one of the Pennsylvania varieties of fire-fly.“ Das damals gebräuchliche Lumen unterscheidet sich geringfügig vom heutigen SI-Lumen.
D. A. Steigerwald u. a.: Illumination with solid state lighting technology. In: IEEE Journal on Selected Topics in Quantum Electronics. vol. 8, no. 2, März/April 2002, S. 310–320. doi:10.1109/2944.999186, S. 310f.
Typische Lichtstärke einer Kerze: I_v ≈ 1 cd isotrop, daher Lichtstrom Φ_v = 4π·I_v ≈ 10 lm (mit grober Rundung 4π ≈ 10).
Cree High Power XHP
Licht.de: Effizienz von Lichtquellen (Übersicht ohne Betriebsverluste). Abgerufen am 19. Januar 2020.
Licht.de: Effizienz von Lichtquellen (Grafik). Abgerufen am 19. Januar 2020.
S. Darula, R. Kittler, C. A. Gueymard: Reference luminous solar constant and solar luminance for illuminance calculations. In: Solar Energy. Volume 79, Issue 5, November 2005, S. 559–565. doi:10.1016/j.solener.2005.01.004. Für die Standard-Hellempfindlichkeitskurve V(λ): 3,7497438·10²⁸ lm, für die 1988 modifizierte Hellempfindlichkeitskurve V_M(λ): 3,7715109·10²⁸ lm.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[3] Die exakte Festlegung ist K_cd = 683 lm/W für Strahlung der Frequenz 540 THz, was in Luft λ = 555,016 nm entspricht. Bei λ = 555 nm hat K seinen maximalen Wert K_m = 683,002 lm/W (Terminologie der IEC)

[IEC_845-21-039-1] International Electrotechnical Commission (IEC): International Electrotechnical Vocabulary. ref. 845-21-039, Luminous flux (abgerufen am 26. März 2021).

[BergmannSchäfer-2] Ludwig Bergmann, Clemens Schaefer: Optik: Wellen- und Teilchenoptik. In: Bergmann-Schaefer Lehrbuch der Experimentalphysik. Band 3. Walter de Gruyter, 2004, ISBN 3-11-017081-7, S. 637 (eingeschränkte Vorschau in der Google-Buchsuche).

[BIPM2019-63-4] BIPM Rapport BIPM-2019/05 Principles governing photometry, 2nd ed., (PDF, 1,01 KiB) – Bericht des BIPM von 2019, Kap. 6.3

[Blevin-5] W. R. Blevin, B. Steiner: Redefinition of the Candela and the Lumen. In: Metrologia. 11, 1975, S. 97–104. doi:10.1088/0026-1394/11/3/001

[Keitz_S25-6] H. A. E. Keitz: Lichtberechnungen und Lichtmessungen. 2. Auflage. Philips Technische Bibliothek, Eindhoven 1967, S. 25.

[BIPM2019-1-7] BIPM Rapport BIPM-2019/05 Principles governing photometry, 2nd ed., (PDF, 1,01 KiB) – Bericht des BIPM von 2019, Kap. 1, S. 3 „Luminous flux is the most fundamental quantity in photometry because it has the simplest relationship with radiant power.“

[CIPM1977-8] Comité International des Poids et Mesures – Procès verbaux des séances. 66^e session. 2^e série, 1977, S. 5–6 (bipm.org [PDF]). (7,4 MB): „Recommandation P 3 (lumen comme unité de base avec une définition en fonction du watt) est celle qui a la préférence de la majorité du CCPR.“ Das CCPR (Comité Consultatif de Photométrie et Radiométrie) ist das zuständige Beratungsgremium des Internationalen Komitees für Maß und Gewicht (CIPM). Der Wortlaut der Empfehlung P 3 befindet sich auf Seite 143 desselben Dokuments.

[Hentschel_128-9] H.-J. Hentschel: Licht und Beleuchtung – Theorie und Praxis der Lichttechnik. 4. Auflage. Hüthig Buch, Heidelberg 1994, ISBN 3-7785-2184-5, S. 128.

[Hentschel_131-10] H.-J. Hentschel: Licht und Beleuchtung – Theorie und Praxis der Lichttechnik. 4. Auflage. Hüthig Buch, Heidelberg 1994, ISBN 3-7785-2184-5, S. 131.

[Hentschel_134-11] H.-J. Hentschel: Licht und Beleuchtung – Theorie und Praxis der Lichttechnik. 4. Auflage. Hüthig Buch, Heidelberg 1994, ISBN 3-7785-2184-5, S. 134.

[Ives_1922-12] H. E. Ives: The Fire-Fly as an Illuminant. In: Journal of the Franklin Institute. vol. 194, no. 2, August 1922, S. 213–230. doi:10.1016/S0016-0032(22)90057-2, „on specimens of the larva of one of the Pennsylvania varieties of fire-fly.“ Das damals gebräuchliche Lumen unterscheidet sich geringfügig vom heutigen SI-Lumen.

[Steigerwald_2002-13] D. A. Steigerwald u. a.: Illumination with solid state lighting technology. In: IEEE Journal on Selected Topics in Quantum Electronics. vol. 8, no. 2, März/April 2002, S. 310–320. doi:10.1109/2944.999186, S. 310f.

[Kerze-14] Typische Lichtstärke einer Kerze: I_v ≈ 1 cd isotrop, daher Lichtstrom Φ_v = 4π·I_v ≈ 10 lm (mit grober Rundung 4π ≈ 10).

[15] Cree High Power XHP

[16] Licht.de: Effizienz von Lichtquellen (Übersicht ohne Betriebsverluste). Abgerufen am 19. Januar 2020.

[17] Licht.de: Effizienz von Lichtquellen (Grafik). Abgerufen am 19. Januar 2020.

[Darula_2005-18] S. Darula, R. Kittler, C. A. Gueymard: Reference luminous solar constant and solar luminance for illuminance calculations. In: Solar Energy. Volume 79, Issue 5, November 2005, S. 559–565. doi:10.1016/j.solener.2005.01.004. Für die Standard-Hellempfindlichkeitskurve V(λ): 3,7497438·10²⁸ lm, für die 1988 modifizierte Hellempfindlichkeitskurve V_M(λ): 3,7715109·10²⁸ lm.