Glan-Thompson-Prisma
Das Glan-Thompson-Prisma (nach Paul Glan und Silvanus Phillips Thompson) ist ein auf Doppelbrechung und Totalreflexion basierender Polarisator aus zwei durch Kanadabalsam zusammengefügten Kalkspat-Teilen, der unpolarisiertes Licht linear polarisiert, wobei die Polarisationsebene parallel zur Schnittebene der beiden Teile ist. Es wurde 1880 von Paul Glan[1] vorgestellt und 1881 von Silvanus Philipps Thompson[2][3] verbessert.[4] Das Prinzip gilt als Verbesserung des Nicol-Prismas.
Aufbau
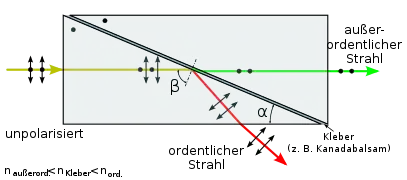
Das Glan-Thompson-Prisma besteht ähnlich wie das zuvor (1828) entwickelte Nicol-Prisma aus einem doppelbrechenden Kristall (ein typisches Material ist Kalkspat). Anders als beim Nicol-Prisma ist der Kristall so in zwei rechtwinklige Prismen geschnitten, dass seine optische Achse parallel zu einer Endfläche liegt, d. h. senkrecht auf den rechtwinkeligen Seitenflächen steht. Die beiden Prismen sind mit einem durchsichtigen Kleber (damals Kanadabalsam) zu einem Quader zusammengefügt.
Der Schnittwinkel der beiden Prismenhälften ist so gewählt, dass der ordentliche Strahl an der Grenzfläche totalreflektiert während der außerordentliche Strahl ohne oder mit vertretbaren Reflexionsverlusten hindurch gelassen wird. Dafür muss der Kleber einen Brechungsindex besitzen, der zwischen dem für den ordentlichen und dem für den außerordentlichen Strahl des doppelbrechenden Materials liegt. Im Fall von Kalkspat bei einer Wellenlänge von λ = 589 nm (Natrium-D-Linie) zwischen 1,486 (außerordentlicher Strahl) und 1,658 (ordentlicher Strahl), beispielsweise von Thompson und früher allgemein oft genutzte Kanadabalsam[5] mit nK = 1,54. Es ergibt sich für den ordentlichen Strahl ein kritischer Winkel von 69,2°. Typische Schnittwinkel liegen daher zwischen 69,2° und 72° (bei größeren Winkeln sinkt der Transmissionsgrad für den außerordentlichen Strahl drastisch), dies entspricht einem Seitenverhältnis Länge zu Breite von ca. 2,5:1 bzw. 3:1.
Funktionsweise
Beim Eintritt in ein Material wird der einfallende Lichtstrahl nach dem Snellius-Brechungsgesetz gebrochen. Aufgrund des anisotropen Brechungsindex im doppelbrechenden Material wird der einfallende Strahl in einen ordentlichen (senkrecht zur optischen Achse des Kristalls polarisierten) und einen außerordentlichen (parallel zur optischen Achse polarisierten) Strahl zerlegt. Da beim Glan-Thompson-Prisma die äußeren Schnittflächen des Kristalls parallel zur optischen Achse liegen, werden bei senkrechtem Einfall beide Strahlen gleich gebrochen – durch den senkrechten Einfall ist der Einfallswinkel gleich dem Brechungswinkel, also 0° (vom Lot aus gemessen). Die beiden Strahlenanteile bewegen sich also auf einem gemeinsam Weg im Kristall, wenn auch wegen des unterschiedlichen Brechungsindexes mit unterschiedlicher Geschwindigkeit.
Treffen nun beide Strahlen auf die innere Schnittfläche, so werden sie aufgrund entsprechend gewählter Materialien unterschiedlich reflektiert. Für den ordentlichen Strahl stellt der Kleber im Vergleich zu Kalkspat ein optisch dünneres Medium dar. Er wird daher an der Schnittfläche totalreflektiert – der kritische Winkel der Totalreflexion wird durch entsprechende Wahl des Prisma-Schnittwinkels überschritten –, so dass er auf eine Außenfläche des Glan-Thompson-Prismas trifft, gebrochen wird und austritt oder von einem gegebenenfalls platzierten Absorber absorbiert wird. Für den außerordentlichen Strahl ist Kalkspat das optisch dünnere Medium. Er durchdringt daher die Schnittfläche gemäß den Fresnel-Gleichungen mit geringen Reflexionsverlusten (T ≈ 98 %, s-polarisiert). Dies wiederholt sich beim Übertritt in die zweite Prismenhälfte. Beim Durchqueren der Kleberschicht erfährt der Strahl einen Strahlversatz, dieser ist aber aufgrund der geringen Dicke der Kleber nur minimal. Beim Austritt aus dem Kristall liegt daher nur noch der linear polarisierte, außerordentliche Strahl vor, dessen Polarisation der Ausrichtung der optischen Achse entspricht.
Der austretende Strahl ist zwar weitgehend, aber nicht vollständig polarisiert. Der Grad der Polarisierung ist außer von den Fertigungstoleranzen auch von den eingesetzten Materialien, welche im Allgemeinen keine idealen Dielektrika sind, und auch von der Dicke der Kleberschicht abhängig. Da ein Lichtstrahl bei der Totalreflexion aufgrund von Stetigkeitsbedingungen der Maxwell-Gleichungen etwas in das nachfolgende optisch dünnere Material eindringt (in Form einer evaneszenten Welle), kann es bei sehr geringen Schichtdicken des Kleber zum sogenannten optischen Tunneleffekt (verhinderte Totalreflexion) kommen. Dabei gelangt in Abhängigkeit von der Schichtdicke ein Teil der eigentlich totalreflektierten Strahlung in die zweite Prismenhälfte. Der ausfallende Strahl ist daher nie hundertprozentig linear polarisiert. Da der Einfluss dieses Effekts jedoch exponentiell mit der Schichtdicke abnimmt, kann er durch eine ausreichend dicke Schicht (typischerweise ≥ 1 mm[5]) nahezu vollständig reduziert werden.
Eigenschaften und Anwendungsbereiche
Sowohl das Nicol-Prisma als auch das ursprüngliche Glan-Prisma / Glan-Foucault-Prisma (Schnittwinkel 38,5°, mit Luftspalt) haben einen vergleichsweise geringen Akzeptanzwinkel (für den Einfall eines konischen Strahlenbündels) von unter 10°.[6] Wie bereits Thompson 1881 bemerkte, treten bei größeren weniger parallelen Strahlbündeln blaue ringförmige Störungen auf.[2] Typische Glan-Thompson-Prisma (Schnittwinkel 72°) haben einen vergleichbaren Akzeptanzwinkel, mit einem geänderten Schnittwinkel sollen aber Akzeptanzwinkel von bis zu 30° (Seitenverhältnis 3:1) oder gar 42° (Seitenverhältnis 4:1) möglich sein.[6][7][5]
Mit Kalkspat und Kanadabalsam können Glan-Thompson-Prismen im Wellenlängen-Bereich von 0,3–2,7 μm eingesetzt werden.[5] In diesem Bereich zeigt dieser Prismen-Typ einen hohen Transmissionsgrad der selektierten Polarisation, die höher und stabiler ist als die von Glan-Taylor- oder dem Nicol-Prisma. Unterhalb von 300 nm beginnt der Kitt Kanadabalsam zu absorbieren. Durch Wahl geeigneter Medien (z. B. Glycerin oder Rizinusöl) kann ein Glan-Thompson-Prisma auch im Ultravioletten genutzt werden; alternativ auch ein Glan-Taylor-Prisma mit Luft statt eines Zwischenmediums.[5][7] Für bessere Transmissionseigenschaften im nahen Infrarot kommt kristalline Glycose oder Glycerin in Frage.[5]
Der rechtwinklige Schliff von Polarisationsprismen des Glan-Typs verbraucht mehr Material als Prismen des Nicol-Typs. Sie waren daher lange Zeit teurer und daher ungebräuchlicher. Dies änderte sich erst als die besseren Eigenschaften der Glan-Typ-Prismen benötigt wurden. Für Präzisionsmessungen haben Glan-Typ-Prismen den Nicol-Typ als Polarisator nahezu komplett verdrängt (für andere Anwendungen kommen eher günstige Polarisationsfolien zum Einsatz).
Alternativ zu Kalkspat kann auch Ammoniumdihydrogenphosphat (ADP) als doppelbrechendes Material eingesetzt werden. Aufgrund der geringeren Ausprägung der Doppelbrechung verringern sich allerdings der Akzeptanzwinkel bzw. die Baulänge erhöht sich.[7]
Abgrenzung zu anderen Polarisationsprismen
Das Glan-Thompson-Prisma gehört zu der Gruppe der Glan-Prismen, die sich von den Nicol-Prismen durch die zur optischen Achse parallelen Einfallsfläche unterscheiden. Damit verbunden ist auch, dass der ordentliche und außerordentliche Strahl im ersten Prisma sich nicht auftrennen, sondern gleich verlaufen. Eine Aufspaltung bei der Strahlen erfolgt erst an der Grenzfläche zum Kleber/Kitt. Des Weiteren ist der Strahlversatz deutlich geringer. Innerhalb der Gruppe der Glan-Prismen unterscheidet sich das Glan-Thompson-Prisma hinsichtlich des eingesetzten Kitts und der damit verbundenen möglichen Bauform sowie der Ausrichtung der optischen Achse der Prismen-Teile, über die die Strahlselektion erfolgt.
Ein Glan-Thompson-Prisma, das statt eines Klebers einen Luftspalt nutzt, wird als Glan-Foucault-Prisma bezeichnet.[5] Es wird vor allem für Hochleistungsanwendungen genutzt, für die das Glan-Thompson-Prisma weniger geeignet ist, da sich hier der Kleber erhitzen und somit zerstört werden kann. Prismenabwandlungen vom Glan-Thompson-Typ sind das Ahrens-Prisma, bei dem zwei Glan-Thompson-Prismen nebeneinander angeordnet sind, und das Grosse-Prisma, im Wesentlichen ein Ahrens-Prisma mit Luftspalt.[5] Das ähnlich aufgebaute Lippich- bzw. Glan-Taylor-Prisma lässt ebenfalls den außerordentlichen Strahl durch, selektiert allerdings aufgrund der um 90° in der Einfallsebene gedrehten optischen Achse den um 90° anders polarisierten Teil. Dazu ähnliche Prismen sind das Marple-Hess-Prisma und das Frank-Ritter-Prisma. Des Weiteren existieren Polarisationsprismen in Strahlteilerbauformen, die nicht auf Totalreflexion basieren: Rochon-, Sénarmont-, Wollaston-Prisma.[5]
Literatur
- Wolfgang Demtröder: Experimentalphysik 2: Elektrizität und Optik. Springer, 2008, ISBN 978-3-540-68210-3, S. 255 f.
- Wilhelm Walcher: Praktikum der Physik. 6. Auflage. 1989, ISBN 3-519-03038-1.
- Horst Stöcker: Taschenbuch der Physik: Formeln, Tabellen, Übersichten. 5. Auflage. Deutsch (Harri), 2004, ISBN 3-8171-1720-5.
- Michael Bass (Hrsg.): Handbook of optics. Volume I, Geometrical and physical optics, polarized light, components and intruments. 3rd Auflage. McGraw-Hill, New York 2010, ISBN 978-0-07-162925-6, 13.3 Glan-Type Prisms.
Einzelnachweise
- Paul Glan: Ueber einen Polarisator. In: Repertorium für Experimental-Physik, für Physikalische Technik, Mathematische und Astronomische Instrumentenkunde. Band 16, 1880, S. 570.
- Silvanus P. Thompson: On a new polarising prism. In: Phil Mag. Band 5, Nr. 12, 1881, S. 349–351, doi:10.1080/14786448108627118.
- Silvanus P. Thompson: On the Nicol Prism and its Modern Varieties. In: Proceedings of the Optical Convention. London 1905, S. 216–240.
- Siegfried Becher: Über den Astigmatismus des Nicols und seine Beseitigung im Polarisationsmikroskop. In: Annalen der Physik. Band 352, Nr. 11, 1915, S. 285–364, doi:10.1002/andp.19153521102.
- Michael Bass (Hrsg.): Handbook of Optics, Third Edition Volume I : Geometrical and Physical Optics, Polarized Light, Components and Instruments. McGraw-Hill Professional, 2009, ISBN 978-0-07-162925-6, S. 13.9–13.12.
- Eugene Hecht: Optics. 4th Auflage. Addison-Wesley, Reading, Mass. 2002, ISBN 0-8053-8566-5, S. 344.
- Heinz Haferkorn: Optik: physikalisch-technische Grundlagen und Anwendungen. 4., bearb. und erw. Auflage. Wiley-VCH, Weinheim 2003, ISBN 3-527-40372-8, S. 434.