Faraday-Effekt
Der Faraday-Effekt ist ein magnetooptischer Effekt. Er beschreibt die Drehung der Polarisationsebene einer linear polarisierten elektromagnetischen Welle in einem Medium, wenn darin ein Magnetfeld parallel zur Ausbreitungsrichtung der Welle herrscht. Es wird auch von Faraday-Rotation gesprochen.

Geschichte
Der Faraday-Effekt wurde von Michael Faraday am 13. September 1845 entdeckt. Er wurde als erster experimenteller Hinweis dafür gedeutet, dass Licht und Magnetismus miteinander in Beziehung stehen. Dass Licht als elektromagnetische Welle beschrieben werden kann, wurde theoretisch wenige Jahre später von James Clerk Maxwell hergeleitet.
Grundlagen
Jede linear polarisierte Welle kann als Überlagerung zweier zirkular polarisierter Wellen gleicher Frequenz mit entgegengesetztem Umlaufsinn interpretiert werden. Verläuft die Ausbreitungsrichtung parallel zu den Magnetfeldlinien, unterscheiden sich in vielen Materialien die Brechungsindizes nLinks und nRechts und deshalb auch die Wellenlängen. Die entsprechenden Formeln lauten
Daraus folgt, dass sich die Polarisationsebene um
weiterdreht, wenn eine Schwingungsdauer, also die Zeit T = 1/f vergangen ist.
Optik
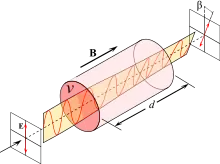
Der Faraday-Effekt tritt im Bereich der Magnetooptik beim Durchgang von Licht durch ein transparentes Medium auf. Ein ähnlicher Effekt, der die Drehung der Polarisationsebene bei Reflexion beschreibt, ist der magnetooptische Kerr-Effekt. Die meisten dielektrischen Materialien (einschließlich Flüssigkeiten) zeigen den Faraday-Effekt, wenn sie einem starken magnetischen Feld ausgesetzt werden. Die Drehung der Polarisationsebene ist umso größer, je stärker die magnetische Flussdichte ist.
Weist das Medium auch ohne ein angelegtes Magnetfeld einen Einfluss auf die Polarisationsebene auf, spricht man von optischer Aktivität.
Der Drehwinkel , um den sich die Polarisationsebene dreht, berechnet sich wie folgt:
ist die Länge des Lichtweges durch die Substanz, die magnetische Flussdichte[1] und die Verdet-Konstante. ist vom Medium und von der Wellenlänge abhängig. Mit einer anderen Verdet-Konstanten , ist statt der Flussdichte die magnetische Feldstärke zu verwenden:[2]
Eine positive Verdet-Konstante führt zu einer mathematisch negativen Drehung, wenn das Magnetfeld parallel zur Ausbreitungsrichtung liegt. Ein antiparalleles Magnetfeld führt dann zu einer mathematisch positiven Drehung (siehe Bild). Das bedeutet, dass sich für eine Welle, die das Medium zweimal in jeweils entgegengesetzter Richtung durchläuft (hin und zurück), die Rotation verdoppelt. Dies ist ein wichtiger Unterschied zur optischen Aktivität links- oder rechtsdrehender Substanzen, durch welche beim Durchlaufen des Mediums in entgegengesetzter Richtung die Rotation wieder rückgängig gemacht wird.
Eine wichtige Anwendung des Faraday-Effektes ist der optische Isolator. Für diese und andere Anwendungen werden Materialien mit hoher Verdet-Konstante verwendet, wie beispielsweise mit Terbium dotierte Gläser und Terbium-Gallium-Granat.
Weiterhin gibt es auf dem Effekt basierende Magnetometer und Stromsensoren, wobei hier Lichtleitkabel verwendet werden.
Funkwellen

Der Faraday-Effekt tritt auch bei vormagnetisierten Ferriten auf und wird in Frequenzbereichen von einigen Gigahertz im Bereich von Mikrowellen zum Aufbau von Gyratoren und zur Realisierung von Faraday-Rotatoren verwendet. Durch die Drehung der Polarisationsebene können so in der Hochfrequenztechnik spezielle Formen von Zweitoren zur Transformation von Impedanzen in ihre dualen Impedanzen realisiert werden.
Der Faraday-Rotator, welcher in diesem Fall in einem Hohlleiter angeordnet ist, weist zwei orthogonal zueinander stehende Hohlleiterausgänge auf, die hineinlaufende Welle lässt sich durch Ändern des Magnetfeldes durch eine Steuerleitung jeweils auf einen der Ausgänge schalten, wie in nebenstehender Abbildung dargestellt.
Durchlaufen Funkwellen die Ionosphäre, bewirkt die Bewegung von ungebundenen Elektronen im Erdmagnetfeld eine Rotation der Polarisationsebene[3] (siehe auch Brechungsindex des Plasmas). Der Drehwinkel ist stets proportional zum Quadrat der Wellenlänge (β = k·λ²) und ist deshalb im Mittel- und Kurzwellenbereich unübersehbar. Über sehr große Entfernungen kann aber auch noch bei 500 MHz eine Drehung über 90° beobachtet werden. Bei den noch höheren Frequenzen der Rundfunksatelliten ist der Winkel aber schon so gering, dass die vertikale bzw. horizontale Polarisation der Übertragungskanäle nur unwesentlich verändert wird.
Astronomie
Faraday-Rotation kommt auch in der Astronomie vor. So wurde beim Quasar PKS 1830-211 am Fuße des Jets Faraday-Rotation nachgewiesen.[4][5]
Literatur
- Karl Küpfmüller, Wolfgang Mathis, Albrecht Reibiger: Theoretische Elektrotechnik. 18. Auflage. Springer, 2008, ISBN 978-3-540-78589-7, doi:10.1007/978-3-540-78590-3.
Einzelnachweise
- Dieter Meschede: Gerthsen Physik. Springer-Verlag, 2015, ISBN 3-662-45977-9, S. 578 (eingeschränkte Vorschau in der Google-Buchsuche).
- Ludwig Bergmann, Heinz Niedrig, Clemens Schaefer: Bergmann-Schaefer Lehrbuch der Experimentalphysik. Band 3 Optik: Wellen- und Teilchenoptik. Walter de Gruyter, 2004, ISBN 3-11-017081-7, S. 620 (eingeschränkte Vorschau in der Google-Buchsuche).
- Effekte der Ionosphäre (PDF; 4,1 MB)
- Tilmann Althaus: Starke Magnetfelder in unmittelbarer Nähe zu Schwarzem Loch beobachtet. Mit den Submillimeterteleskopen von ALMA wurden erstmals starke Magnetfelder am Fußpunkt eines Jets eines massereichen Schwarzen Lochs in einer fernen Galaxie nachgewiesen. In: Spektrum der Wissenschaft. 16. April 2015, abgerufen am 31. Mai 2015.
- Ivan Marti-Vidal, Sebastien Muller, Wouter Vlemmings, Cathy Horellou, Susanne Aalto: A strong magnetic field in the jet base of a supermassive black hole. 15. April 2015, abgerufen am 3. März 2016 (englisch).