APL (Programmiersprache)
APL (A Programming Language) ist eine üblicherweise interpretierende Programmiersprache, deren Syntax überwiegend aus Symbolen besteht. Sie wurde von Kenneth E. Iverson und seinen Kollegen[1] bei IBM in den 1960er Jahren als algorithmische Notation (u. a. für den Mathematikunterricht)[2] und als Entwurfssprache für Großrechner entwickelt.
| APL | |
|---|---|
| Paradigmen: | funktional, strukturiert, modular |
| Erscheinungsjahr: | 1964 |
| Designer: | Kenneth E. Iverson |
| Entwickler: | Kenneth E. Iverson |
| Typisierung: | dynamisch |
| Wichtige Implementierungen: | Dyalog APL, IBM APL2, APL2000, Sharp APL, APLX, NARS2000, GNU APL |
| Dialekte: | A+, Dyalog APL, APLNext, ELI, J |
| Standardisierungen: | ISO8485 (1989), ISO/IEC13751 (2001) |
| Beeinflusst von: | Mathematische Notation |
| Beeinflusste: | J, K, Mathematica, Matlab, Nial, PPL, Q, R, S |
Geschichte
.jpg.webp)
Mit dem Buch A Programming Language aus dem Jahr 1962 gab Kenneth Iverson den Anstoß zur Verwendung eines neuen Konzepts in der Programmierung. Bevor der erste Interpreter verfügbar war, diente APL bereits als Metasprache für die Beschreibung der Architektur des damals neu entwickelten Computersystems IBM System/360 aus der Sicht des Programmierers.[3] Ab 1965 wurde APL als Programmiersprache auf Großrechnern (z. B. IBM System/360) implementiert und den Kunden als Timesharing-Option angeboten. Zu jener Zeit wurden IBM-Kugelkopf-Schreibmaschinen als „Terminal“ verwendet. Daher hatte der ursprüngliche Zeichensatz nur (kursive) Großbuchstaben.[4]
Ab 1975 gab es eine Implementierung auf der IBM 5100, einem Vorläufer des PC, der bereits ein Mikrocomputer war. Obwohl die Maschine nach damaligen Maßstäben als durchaus leistungsfähig galt, lief APL auf ihr verhältnismäßig langsam, da es sich um eine Emulation des Mainframe-APL-Interpreters handelte.
Die ersten Implementierungen auf PCs benötigten ein Spezial-EPROM, damit der APL-Zeichensatz angezeigt werden konnte. Der APL-Zeichensatz wurde ursprünglich so gewählt, dass die Symbole möglichst selbsterklärend sind, dass sich also die Funktionen aus den Symbolen intuitiv herleiten lassen. Seit einigen Jahren wird der Begriff APL auch als Array Processing Language interpretiert.
Besonderheiten
Operatoren und spezielle Zeichen
APL verwendet spezielle Operatoren, bzw. Befehle, die jeweils die Funktion haben, nicht nur einzelne Zahlen-Werte zu bearbeiten, sondern bei Bedarf ganze Vektoren und Matrizen, z. B. 2 Matrizen zu addieren oder das Skalar-Produkt von 2 Vektoren zu berechnen. Für jeden dieser Operatoren gab es ein spezielles Zeichen, wodurch insgesamt ein erweiterter Zeichensatz benötigt wurde und zwar sowohl auf der Tastatur, im Speicher und auf dem Bildschirm – seitdem es solche gab – wie auch auf dem Drucker. Es gab damals noch keine Laser- oder Inkjet-Drucker, die man programmieren kann, quasi jedes beliebige Zeichen zu generieren. Die Verwendung solcher Zeichen mit der Funktion von Operatoren ermöglichte zwar einen extrem knappen, aber für Außenstehende auch kryptischen Code, der viele Leute abschreckte und nicht zwingend war. Man hätte auch reservierte Worte als Operatoren verwenden können.
Interaktivität
APL war von Anfang an interaktiv: Nach der Eingabe eines Befehls (z. B. einer Rechenanweisung 1234 − 777) drückt man die Entertaste, der Befehl wird vom Interpreter ausgeführt und das Ergebnis angezeigt. Eine spezielle Anweisung für die Ausgabe des Ergebnisses, wie z. B. der PRINT-Befehl in BASIC, ist nicht nötig, existiert aber für den Fall, dass ein Ergebnis angezeigt werden soll, das normalerweise nicht angezeigt würde (z. B., wenn einer Variablen ein Wert zugewiesen wird).
Tritt ein Fehler auf, erhält man eine entsprechende Meldung. Man kann seine Eingabe modifizieren und erneut ausführen. Die dadurch mögliche direkte Interaktion mit dem Computer ist bis heute einer der großen Vorteile von APL als Entwicklungswerkzeug.
Aus heutiger Sicht klingt dies trivial, aber APL war eine der ersten Programmiersprachen, die diesen Luxus bot: Konkurrierende Sprachen waren noch nicht interaktiv, sondern mussten vor der Ausführung eines Programms jeweils kompiliert werden.
Programmcode
Folgen von Befehlen lassen sich zu Funktionen zusammenfassen. Funktionen können wiederum andere Funktionen aufrufen. In der Tat ist APL eine der ersten funktionalen Programmiersprachen. Näheres und ein Beispiel siehe unten.
Bis in die 1990er Jahre fehlten APL die Kontrollstrukturen der „Strukturierten Programmierung“. Logik musste durch Sprunganweisungen realisiert werden. In APL werden Kontrollstrukturen seltener als in anderen imperativen Programmiersprachen verwendet, einerseits weil APL-Funktionen nicht nur Skalare, sondern Datenstrukturen beliebiger Dimension verarbeiten, andererseits, weil es den Operator Each bietet.
Datentypen
APL kennt mindestens die Datentypen Char, Bool, Int und Float, allerdings muss der Programmierer dies nicht berücksichtigen, denn der Interpreter wandelt die Datentypen automatisch um, wann immer dies notwendig ist. Dies bedeutet auch, dass APL keine Typprüfung kennt.
Der Datentyp von Variablen muss nicht eigens deklariert werden, man kann einer Variablen eine Gleitkommazahl zuweisen (oder einen Vektor oder eine Matrix von Gleitkommazahlen) und danach einen Text, ohne dass es zuvor einer besonderen Anweisung bedarf.
Speicherverwaltung
Auch die Speicherverwaltung wird vom Interpreter übernommen. Ein APL-Programmierer muss sich während des Programmablaufs weder um das Reservieren noch um das Freigeben von Speicher kümmern. Der Arbeitsspeicher wird im sogenannten Workspace für Variablen und Programme insgesamt zur Verfügung gestellt, er kann beim Programmstart festgelegt und in manchen APL-Produkten auch dynamisch erweitert werden.
Array-Verarbeitung
Fast alle Funktionen in APL sind auch nicht-skalar ausgelegt. Dies bedeutet, dass Funktionen nicht nur auf einzelne Skalare (Zahlen oder Characters), sondern auch auf Vektoren (Zahlenreihen), Matrizen (Tabellen) und mehrdimensional angeordnete Daten (Arrays) sowie auf Listen angewendet werden können.
Beispiele (die eingerückte erste Zeile ist die Benutzereingabe, die zweite Zeile die Antwort des APL-Interpreters)
Viele Programmiersprachen erlauben die Addition zweier Skalare:
2 + 3 5
APL gestattet aber auch die Addition Vektor und Skalar:
2 3 4 + 3 5 6 7
und die Addition zweier Vektoren:
2 3 4 + 5 6 7 7 9 11
Ausführung und Rangfolge
Es gibt in APL nur eine einzige Rangfolgenregel: Alles wird von rechts nach links abgearbeitet. Ausnahme: Ausdrücke in Klammern werden zuerst abgearbeitet. Daher gilt:
10×2+3 50
aber:
(10×2)+3 23
Variablen
In APL müssen Variablen nicht deklariert oder typisiert werden (siehe Datentypen). Eine Variable wird erzeugt, indem man einen Namen, gefolgt von einem Zuweisungspfeil (←), gefolgt vom Wert bzw. den Werten der Variablen eingibt:
XWERT←456.78
YVECT←56 23 81.8 796 0.014 8.9 20 1
TEXT1←'Dies ist ein Text'
MATRIX←2 4ρYVECT
(der Operator ρ, genannt rho, verwandelt den 8-gliedrigen Vektor YVECT in eine Matrix mit 2 Zeilen und 4 Spalten. So lassen sich auch Arrays mit mehr Dimensionen bilden.)
Das Konzept der Konstanten, also unveränderbar deklarierter Werte, gibt es in APL nicht, es kann aber simuliert werden durch eine Funktion, die keine Argumente benötigt und ein explizites Ergebnis zurückliefert.
Geltungsbereich
Jede Zuweisung erzeugt eine globale Variable, d. h. die Variable ist im gesamten Programm sicht- und änderbar. Man kann den Geltungsbereich von Variablen aber einschränken, indem man den Namen der Variablen in die Kopfzeile einer Funktion aufnimmt. Eine solche Variable wird als lokal bezeichnet, da sie nur zur Laufzeit der Funktion sichtbar ist.
Wenn allerdings eine Funktion F1 eine lokale Variable A definiert und anschließend eine Funktion F2 aufruft, dann ist A innerhalb von F2 sicht- und änderbar, was heute als Designmakel gilt. Die Direct Functions in Dyalog APL verhalten sich allerdings anders: Dort sind lokale Variablen tatsächlich im engeren Sinne lokal und auch in aufgerufenen Funktionen unsichtbar.
Arrays
Daten jeder Art werden in APL Arrays genannt. Arrays können unterschiedliche Dimensionen haben. Ein einzelner Wert wird Skalar genannt. Mehrere Werte nebeneinander bilden einen Vektor. Der Operator zur Verkettung (Konkatenieren) mehrerer Skalare ist das Komma. Dabei ist es auch möglich, einen einzelnen Wert mit einer Leeren Menge zu verketten und so einen Vektor zu erhalten, der aus einem einzigen Element besteht. Auch leere Vektoren sind erlaubt: Das sind Vektoren, die überhaupt kein Datenelement enthalten, sondern nur die Strukturinformation.
Werte, die in Zeilen und Spalten angeordnet sind, bilden Tabellen, auch Matrizen oder zweidimensionale Arrays genannt.
Die Dimension eines Arrays wird in APL mit dem griechischen Buchstaben ρ (Rho) angegeben. Wenn von dem „Rank“ eines Arrays die Rede ist, meint man die Anzahl der Dimensionen des Arrays, also Rho von Rho. Demzufolge ist der Rank eines Skalars 0, der eines Vektors 1, der einer Tabelle 2, und so weiter.
Die Ebenen eines dreidimensional angeordneten Arrays heißen Planes. Es sind Arrays mit n Dimensionen möglich, die Anzahl ist nur begrenzt durch die maximale Größe der Integer-Indizierung (231-1) und den zur Verfügung stehenden Speicherplatz.
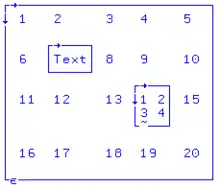
Im Jahre 1986 brachte IBM ein erheblich erweitertes APL mit dem Namen APL2 auf den Markt. Die Erweiterung bestand hauptsächlich darin, dass jedes Element eines Arrays aus beliebigen anderen Datenstrukturen bestehen kann (Nested Array). Damit ergeben sich verschachtelte Strukturen. Zur Veranschaulichung befindet sich rechts ein Beispiel. Es handelt sich dabei um eine bereits behandelte, numerische Matrix mit 4 Zeilen und 5 Spalten. Jedoch besteht das 2. Element der 2. Zeile aus einem Textvektor und das 4. Element der 3. Zeile aus einer 2x2-Matrix. Es lassen sich somit auch die Textlabels mit den numerischen Werten zu einer Tabelle verknüpfen. APL2 eröffnete die Möglichkeit, auch mixed arrays sowie einfache und komplexe Listen zu erzeugen.
Im Zuge dieser Erweiterung wurden auch neue sogenannte „primitive Funktionen“ (primitive funktions) zur Bearbeitung der neuen Datenstrukturen eingeführt sowie die alten Funktionen angepasst und in ihrem Geltungsbereich erweitert. Andere APL-Hersteller brachten ähnliche Erweiterungen ihrer Implementierungen heraus, wobei feine Unterschiede die Portierung eines Programms zu einer anderen Implementierung erschweren. Heute gilt die APL2-Implementation als Referenz für alle Hersteller, man bemüht sich um größtmögliche Kompatibilität.
Funktionen und Operatoren
APL kennt sowohl Funktionen als auch Operatoren, aber die Bedeutung der Begriffe ist anders als in der Mathematik: Funktionen werden auf Daten angewendet, Operatoren auf Funktionen und Daten. Funktionen liefern Daten zurück, Operatoren sogenannte „abgeleitete Funktionen“ (engl.: derived function).
Beispiel
Das Zeichen slash (/) steht für den Operator reduce. Operatoren erwarten einen oder zwei Operanden. Wird nur ein Operand verwendet, dann muss er links neben dem Operator stehen:
+/
In diesem Beispiel ist der Operand die Funktion „Plus“. Zusammen mit dem Operator wird die abgeleitete Funktion Summiere gebildet.
Angewendet auf einen Vektor:
+/ 3 4 5
bewirkt der Operator Reduce, dass der Operand zwischen die einzelnen Bestandteile des Vektors eingefügt wird. Abstrakt ausgedrückt:
f/ n1 n2 n3 == n1 f n2 f n3
und im konkreten Beispiel (das Ergebnis steht darunter):
+/ 3 4 5 == 3 + 4 + 5 12
Wie mächtig dieses Konzept ist, wird aber erst bei Betrachtung eines anderen Operators klar: Expand (backslash, \) verwendet den Operanden in der gleichen Weise wie Reduce, erzeugt aber Zwischenergebnisse und reduziert den Rang des Ergebnisses nicht (Reduce verwandelt einen Vektor in ein Skalar, eine Matrix in einen Vektor und so weiter – dies verringert die Notwendigkeit von Programmschleifen):
+\ 3 4 5 3 7 12
Weitere Beispiele
×/ 3 4 5
60
×\3 4 5
3 12 60
-/3 4 5
4
-\3 4 5
3 -1 4
Es gibt auch Operatoren, die zwei Operanden verlangen. Der Operator Outer Product (.) ist ein solcher Operator. Verwendet man als Operanden die Funktionen Plus (+) und Mal (×), dann entsteht in APL die Matrizenmultiplikation:
1 2 3 +.× 40 50 60 320

Das funktioniert genauso mit Matrizen. Um dies zu demonstrieren, sind in dem Bild einige Zeilen aus einer APL-IDE (hier Dyalog APL/W) dargestellt. Es werden neben + und × drei APL-Funktionen verwendet:
- Der nach links weisende Pfeil symbolisiert in APL die Zuweisung eines Wertes auf einen Variablennamen.
- Das einem i ähnelnde Zeichen ι (Iota) steht für die Funktion Indexvektor bilden. Im ersten Anwendungsfall wird eine Zahlenkette von 1 bis 6 erzeugt.
- Das dem Buchstaben p ähnelnde Zeichen ρ (rho) steht für die APL-Funktion shape und formatiert die rechts angegebenen Daten. Die Anzahl der Achsen wird links von dem Zeichen angegeben. Im ersten Anwendungsfall wird eine Matrix mit zwei Zeilen und drei Spalten erzeugt.
- Die Formel „+.ד symbolisiert das Matrizenprodukt.
Selbstdefinierte Funktionen
Zusätzlich zu den eingebauten Funktionen (primitive functions) kann man seine eigenen Funktionen schreiben, die dann selbstdefinierte Funktion (user-defined function) genannt werden. Eine solche Funktion kann null, ein oder zwei Argumente verlangen und heißt entsprechend „niladische“, „monadische“ oder „dyadische“ Funktion. Gemäß ihrer Abstammung von der mathematischen Notation erwarten monadische APL-Funktionen ihr Argument rechts und dyadische Funktionen rechts und links.
Die Funktion kann einen Wert zurückliefern.
Beispiel für eine dyadische Funktion:
R ← S Runde Z
Dabei sei „S“ die Zahl der Dezimalstellen, auf die das Argument „Z“ (eine reelle Zahl) zu runden ist; das Ergebnis steht in R. Anwendung:
2 Runde 3.14159265 3.14
Funktionen können sich über mehrere Zeilen erstrecken. In Funktionen können andere Funktionen aufgerufen werden. Verzweigungen erfolgten ursprünglich mittels (evtl. bedingten) Sprungbefehlen und Zielmarken (labels). Heute wird diese Technik kaum noch verwendet: Außer APL2 bieten alle modernen Implementationen Kontrollstrukturen.
Programmbeispiel zur Illustration der Wirkungsweise von APL
R ← S Runde Z [1] ⍝ Runde eine reelle Zahl Z auf S Stellen [2] ⍝ Standardwert für S ist 2, wenn der Wert beim Aufruf nicht spezifiziert wurde [3] →(0≠⎕NC'S')/RN [4] S←2 [5] RN: R←(10*-S)×⌊0.5+Z×10*S
Diese Funktion und ihre Anwendung sollen die Eigenschaften von APL erläutern:
Erläuterung des Programmbeispiels
- Zeile 0: Definition der Funktion mit zwei Argumenten S („Stellen“) und Z („Zahl“) und einem expliziten Ergebnis R.
- Zeilen 1 und 2: Kommentarzeilen (erkennbar an der „Lampe“ ⍝ als erstem Zeichen).
- Zeile 3: Mit einer Bedingung wird geprüft, ob die NameClass („eingebaute Funktion“ ⎕NC) des Namens S ungleich 0 ist. 0 bedeutet „nicht definiert“. Die Verzweigung zur Marke RN gilt, wenn die Bedingung in Klammern = 1 ist, andernfalls wird RN (das einfach nur die Zeilennummer 5 ist), durch die normale APL-Anweisung 0/RN auf den „leeren Vektor“ reduziert („/“ ist der Operator reduce) und es erfolgt keine Verzweigung.
- Zeile 4: Wenn die Bedingung in Zeile 3 nicht erfüllt ist (= Wert ist unbekannt), wird S auf 2 gesetzt.
- Zeile 5: Hier findet die eigentliche Rundung statt. Kennzeichnend ist das „Weiterreichen“ errechneter Werte von rechts nach links, z. B. die Multiplikation des Parameters Z mit den Rundungsstellen S (Z×10*S). Der dadurch erzeugte um S Zehnerpotenzen größere Wert wird anschließend (also links davon) kaufmännisch (Addition von 0.5) gerundet (⌊-Funktion, genannt „floor“) und somit von weiteren Dezimalstellen befreit, so dass er nun ein ganzzahliger Wert ist. Das Ergebnis wird in die links stehende Multiplikation mit (10*-S) weitergereicht, die den Wert wieder um S Zehnerpotenzen verringert. Dies ist das Ergebnis R der Funktion.
Wirkungsweise bzw. Anwendung
Beispiele:
1 Runde 3.14159265 3.1 Runde 3.14159265 3.14 3 Runde 3.14159265 77.123 99.9 3.142 77.123 99.900 Runde 2 2 ρ(ι4)÷7 0.14 0.29 0.43 0.57
- Erstes Beispiel: Anwendung der Funktion auf Pi, Rundung auf 1 Stelle (siehe auch weiter oben).
- Zweites Beispiel: Rundung von Pi auf zwei Stellen, Test des Default-Wertes (linkes Argument fehlt).
- Drittes Beispiel: Rundung eines Vektors auf drei Stellen (rechts fehlende Nullen werden ergänzt).
- Viertes Beispiel: Rundung einer Matrix (Tabelle) auf zwei Stellen (Default) – zwei Zeilen und zwei Spalten erzeugt durch die Funktion ρ aus der Division der ersten vier natürlichen Zahlen (ι4, Funktion iota) durch 7.
Die Funktion Runde kann nicht nur wie oben gezeigt interaktiv ausgeführt werden, sie kann auch in anderen Programmen verwendet werden:
X ← 4 Runde +/MAT
Dabei sei MAT eine Tabelle mit beliebigen Zahlen, die durch die „Summenreduktion“ (+/) spaltenweise summiert wird. Die entstehenden n-stelligen Zahlen (ein Vektor) werden auf 4 Dezimalen gerundet der Variablen X zugewiesen. Stattdessen könnte man auch damit weiterrechnen, sie beispielsweise mit 2 multiplizieren:
2 × 4 Runde +/MAT
„Moderne“ Sprachkonzepte: Rekursion und Kontrollstrukturen
Eine Stärke von APL ist die Rekursion, der Aufruf einer Funktion innerhalb ihrer selbst. Dies war in der ursprünglichen Implementierung von APL bereits enthalten (im Gegensatz zu den meisten damaligen Programmiersprachen wie COBOL oder FORTRAN).
Beispiel (ohne Zeilennummern) unter Verwendung „moderner“ (in anderen APL-„Dialekten“ später eingefügte Kontrollstrukturen):
Z ← FAKULTÄT N ⍝ Da n! = n × (n-1)!, muss (am Anfang) die Rekursion ⍝ bei n=1 "gestoppt" werden (1! = 1) :If N <= 1 Z←1 :Else Z←N×FAKULTÄT N-1 :EndIf
Anm.: Wegen der Verarbeitungsreihenfolge muss „n-1“ nicht in Klammern stehen (kann aber).
Mächtigkeit und Lesbarkeit
APL ist mächtig: Es gibt (abhängig von der Version) rund 70 primitive, das heißt im Interpreter verankerte (im Gegensatz zu selbst definierten) Funktionen. Diese werden durch etwa 50 Symbole dargestellt, von denen rund 20 Symbole zwei verschiedene Funktionen repräsentieren, in Abhängigkeit davon, ob sie mit einem oder zwei Argumenten aufgerufen werden.
Beispiel:
- In 8 ÷ 4 wird die Funktion „÷“ dyadisch als Division verwendet. Das Ergebnis ist 2.
- In ÷.25 wird die Funktion „÷“ monadisch verwendet; sie liefert den Kehrwert des rechten Arguments. Das Ergebnis ist 4.
Die meisten der in APL „eingebauten“ Funktionen wirken sowohl auf Skalare als auch auf Vektoren, Matrizen und Arrays. Wo in anderen Programmiersprachen Schleifen verwendet werden müssen, um eine Menge von Werten zu verarbeiten, genügt in der Regel bei APL der Einsatz einer primitiven Funktion. Darüber hinaus können viele dieser Funktionen mittels Operatoren erweitert werden.
Neben den primitiven Funktionen, die immer aus einem einzelnen Zeichen bestehen, gibt es eine große Anzahl von System-Funktionen und -Variablen. Datum und Uhrzeit sind z. B. in einer Systemvariablen ⎕TS (für TimeStamp) abfragbar. Systemvariablen gehören nicht zum „primitiven“ Sprachumfang, sondern sind abhängig von der Implementation. Auch Systemfunktionen sind teilweise implementationsabhängig. Sie stellen beispielsweise Schnittstellen zu anderen Programmiersprachen und zum Betriebssystem bereit.
Definierte Funktionen passen sich nahtlos in dieses Konzept ein. Sie können monadisch oder dyadisch sein und ohne spezielle Syntax mit den primitiven Funktionen zusammen in einem Statement verwendet werden. Es können sogar selbst programmierte Funktionen als Argumente eines Operators verwendet werden oder Operatoren selbst programmiert werden.
Da die primitiven Funktionen von APL nur aus einem einzigen Zeichen bestehen und diese Funktionen zudem sehr mächtig sind, kann keine andere Sprache mit vergleichbarer Kürze und Stringenz aufwarten. Wo in anderen Programmiersprachen viele Zeilen vonnöten sind, reicht bei APL häufig schon eine Anweisung mit einigen Symbolen aus.[5]
Dies sind die berühmt-berüchtigten „one-liners“, an denen viele APL-Programmierer ihr „Denkzeug“ („APL as a tool of thought“) geschärft haben. Ken Iverson selbst hat einen one-liner geschaffen, der eine Liste der ersten Primzahlen bis höchstens N erstellt:[6]
(2 = 0 +.= T ∘.| T) / T ← ιN
Es existieren noch extremere Beispiele. So gibt es eine APL-Lösung des n-Damen-Problems ebenfalls in einer (!) Zeile. Kritiker sprechen von APL gelegentlich als von einer „Write-once-read-never“-Sprache. Diesem Urteil liegt ein Missverständnis zugrunde: Wenn in einer Zeile APL soviel passiert wie in zwei Seiten C-Code, dann sollte man realistischerweise davon ausgehen, dass diese eine Zeile zum Verständnis etwa die gleiche Zeit benötigt wie die zwei Seiten C-Code.
APL hat sich besonders in Bereichen bewährt, in denen sich die Anforderungen konstant und schnell ändern: Versicherungen, Hedge-Fonds, Portfolio-Verwalter sowie Prototyping für neue Anwendungen.
Die verwendeten Symbole, die Kürze der Formulierung und die variable Manipulation abstrakter Objekte (die erwähnten Skalare, Vektoren, Matrizen und so weiter – sowohl in Zahlen- wie in Textform und sogar gemischt) machen APL zu einer Sprache für Mathematiker (wofür sie ja auch anfangs konzipiert war). Sie erfordert abstraktes Denken und räumliches Vorstellungsvermögen, ist dadurch aber auch einfach und sehr elegant.
Ausführungsgeschwindigkeit
Da APL interpretiert wird, kann es vergleichsweise langsam in der Ausführung sein. Dies macht sich besonders dann unangenehm bemerkbar, wenn ein APL-Programm sich um einzelne Datenteilchen kümmern muss, zum Beispiel in einem KeyPress-Event-Handler. Andererseits umfasst APL einen großen Vorrat hochspezialisierter Funktionen, die für die Verarbeitung großer Arrays optimiert sind. Werden diese Funktionen auf große Datenmengen angewendet, dann können APL-Programme wie auch andere Interpreter-Programme sehr schnell sein.
Als funktionale Sprache ist APL prinzipiell geeignet, Multiprozessormaschinen auszunutzen. In diesem Bereich gibt es derzeit die größten Weiterentwicklungen der am Markt erfolgreichen APL-Implementationen.
Entwicklung und aktuelle Situation
Die Zeitschrift APL Quote-Quad stellte das erste schriftliche Kommunikationsmittel für APL-Anwender außerhalb von IBM dar, und dieses hausgemachte Mitteilungsblatt war definitiv ein Keimzelle für die Organisation von APL-Anwendern unter der Ägide der Association for Computing Machinery (ACM).[7]
Bis etwa 1985 war IBM mit ihrem APL2-Interpreter auf PCs wie auf Mainframes der führende Anbieter. In den folgenden knapp 10 Jahren war APL sehr erfolgreich, wurde aber nicht nennenswert weiterentwickelt. Erst seit etwa 1992 haben kleinere Software-Unternehmen (APL2000, Dyalog APL, später auch MicroAPL) APL kontinuierlich weiterentwickelt. Mittlerweile haben diese Implementierungen IBMs APL2 in Sachen Leistungsfähigkeit deutlich hinter sich gelassen. Allerdings ist APL2 die einzige APL-Implementierung, die (auch) auf Mainframes läuft.
Die vielleicht derzeit beste Implementierung, Dyalog APL, wurde von Microsoft in den Kreis der anerkannten .NET-Sprachen aufgenommen. IBM APL2 ist dagegen erste Wahl in IBMs Websphere-Welt.
Besondere Bedeutung hat APL2 heute vor allem noch in der Banken-, Versicherungs- und der Tourismusbranche sowie in Forschung und Entwicklung.
Heute wird APL in kleinen Projekten von spezialisierten Software-Unternehmen eingesetzt sowie als Werkzeug von Fachleuten, die sich eher als Systemanalytiker oder Business-Analysten denn als Programmierer bezeichnen. Auch in den Fachabteilungen größerer Unternehmen, Forschungsinstituten und an Universitäten wird es noch immer erfolgreich genutzt.
„APL is alive and well“ und hat ein eigenes Wiki.[8]
2012 konnte das Computer History Museum mit der Erlaubnis von IBM den Assembler-Quelltext von APL in der 1969–1972 “XM6” Version für System/360 veröffentlichen.[9]
Die Firma Log-On Software kündigte im Januar 2021 Log-On APL2 für den April 2021 an.[10] Bei IBM ging der Support für das Produkt APL2 im September 2021 zu Ende.[11]
J und APL
In seinen späten Jahren hat der Hauptdesigner von APL, Ken Iverson, einen zweiten Versuch gewagt. Das Ergebnis ist die Programmiersprache J, die nichts mit Microsofts nicht mehr unterstützter Programmiersprache J# zu tun hat. Diese Sprache ähnelt in ihren Konzepten sehr stark APL, verwendet aber ausschließlich Zeichen des ASCII-Zeichensatzes. Dies wird von den Anhängern als gewaltiger Fortschritt angesehen, von Kritikern aber abgelehnt, da die Verständlichkeit vermindert und Selbsterklärung der Symbole nicht ausgenutzt werden.
Einzelnachweise
- Falkoff, A.D., K.E. Iverson, The Design of APL, IBM Journal of Research and Development, Volume 17, Number 4, 1973-07.
- Iverson K.E.," Notation as a tool of thought (Memento vom 24. August 2012 im Internet Archive) (PDF; 2,2 MB)", Communications of the ACM, 23: 444-465 (August 1980).
- A. D. Falkoff, K. E. Iverson, E. H. Sussenguth: A formal description of SYSTEM/360. In: IBM Systems Journal. Volume 3, Issue 2 (1964).
- Die Schreibmaschine hat einen begrenzten Zeichenvorrat. Spezielle Symbole wurden deshalb durch Übereinandertippen zweier Zeichen erzeugt. Beispiel: Das Zeichen ⍝ wird durch die Folge ⋂ [Rücktaste] ° erzeugt.
- Als Beispiel möge ein Video auf YouTube dienen, in dem Schritt für Schritt zwei einzeilige APL Funktionen entwickelt werden: die erste Funktion berechnet die nächste Generation gemäß den Regeln für Conways Spiel des Lebens, die zweite Funktion stellt das Spiel dar: Conway’s Game Of Life in APL
- One-liner Wars in APL
- Arlene E. Azzarello: QUOTE-QUAD: The Early Years., APL Press, Palo Alto, 1982-11.
- APL wiki
- Len Shustek: The APL Programming Language Source Code (englisch) computerhistory.org. 10. Oktober 2012. Abgerufen am 15. Oktober 2013.
- Log-On Software Announces Log-On APL2. Database Trends and Applications, 8. Februar 2021, abgerufen am 24. Oktober 2021 (englisch).
- Software withdrawal and support discontinuance. IBM APL2, IBM APL2 Application Environment, and IBM Workstation APL2 for Multiplatforms. In: ibm.com. 26. Januar 2021, abgerufen am 24. Oktober 2021 (englisch).
Literatur
- Bernard Legrand: Mastering Dyalog APL. 2009, ISBN 978-0-9564638-0-7.
- Kenneth E. Iverson: A Programming Language. Wiley, 1962, ISBN 0-471-43014-5.
- James A. Brown, Sandra Pakin, Raymnod P. Polivka: APL2 at a Glance. Prentice Hall, 1988, ISBN 0-13-038670-7.
- Hans Lochner: APL2-Handbuch. Springer Verlag, 1989, ISBN 978-3-540-50677-5.
- Wulf-Dieter Wagner: Software-Engineering mit APL2. Springer Verlag, 1992, ISBN 3-540-54406-2.
- Hanspeter Bieri und Felix Grimm: Datenstrukturen in APL2. Springer Verlag, 1992, ISBN 0-387-55747-4.
- Bernhard Legrand: Les APL étendus. Masson, Paris 1994.
Weblinks
Implementierungen
Über APL
- APL Wiki
- APL-Germany e. V. – Deutsche Anwendervereinigung
- Über APL
- Conways Game of life in APL
- APL demonstration Professor Bob Spence, Imperial College London, 1975.
- The Origins of APL mit Ken Iverson und Adin Falkoff, 1974
Syntax
- APL2-Handbuch (PDF; 702 kB)